Die experimentelle Bestätigung des Relativitätsprinzips

Die experimentelle Bestätigung des Relativitätsprinzips;

von A. H. Bucherer.

(Hierzu Taf. VII, Flg. 1 u. Taf. VIII. Fig. 2 und Versuch Nr. 7 u. 15.)

---

Zur Zeit, als ich meine Versuche begann, lagen die Ergebnisse der Kaufmannschen Messungen bereits vor. Die Lorentzsche Theorie schien widerlegt; die Hypothese des starren Elektrons, die auf der ursprünglichen Maxwellschen Theorie basierte und meine Hypothese des bei konstantem Volumen deformierten Elektrons ließen sich damals gleich gut mit dem Experiment in Einklang bringen. Aber die ursprüngliche Form der Maxwellschen Theorie war bereits auf anderen Erfahrungsgebieten endgültig besiegt und andererseits stellten sich meiner Hypothese Schwierigkeiten auf dem Gebiete der Dispersionserscheinungen entgegen. Der Kern dieser Schwierigkeiten war die unvollständige Erfüllung des Prinzips der Relativität der Bewegungen, und so drängte sich die Frage auf, ob sich ein neues Relativitätsprinzip unter Beibehaltung der Maxwellschen Differentialgleichungen ableiten ließe, das mit den Kaufmannschen Messungen in Einklang sein sollte. Da Lorentz nachgewiesen hatte, daß seine Lösung des Problems eindeutig sei, so konnte man nur hoffen, durch eine abweichende Deutung der Gleichungen zum Ziele zu gelangen. In der Tat ist der von mir vorgeschlagene Ausweg^[1] nur eine Rechenvorschrift. Die Kräfte, die bewegte Elektronen in elektromagnetischen Feldern erfahren, weichen von den anderweitig angenommenen ab. So wirkt auf ein Elektron im magnetischen Felde die Kraft:

(1)	$K={\frac {\varepsilon Hu\sin \alpha }{1-{\dfrac {u^{2}}{v^{2}}}\cos ^{2}\alpha }}.$

Hier bedeutet $\alpha$ den Winkel, den die Bewegungsrichtung mit der Feldrichtung bildet. Da das starre Elektron zugrunde gelegt wird, so wird bei $\alpha =R$ die Ablenkung dieselbe sein wie in dem von Kaufmann realisierten Falle. Dagegen müßte bei schief gegen das Feld gerichteten Strahlen eine Abweichung von dem nach anderen Theorien zu erwartenden Verhalten sich zeigen. Es handelte sich deshalb zunächst um die Entwickelung einer Methode, die eine Untersuchung der Ablenkung schief gegen die Feldrichtung fliegender Elektronen gestattete.

§ 1. Die Versuchsmethode.

Das Prinzip der Methode läßt sich wie folgt beschreiben. Becquerelstrahlen, von einer punktförmigen Strahlungsquelle ausgehend, durchfliegen ein Kondensatorfeld $F$, dessen Kraftwirkung durch Überlagerung eines den Platten parallelen gleichförmigen Magnetfeldes $H$ innerhalb des Kondensators kompensiert wird. Nach dem Austritt aus dem Kondensator wirkt das Magnetfeld allein und lenkt die Strahlen ab, die dann auf einen photographischen Film fallen (vgl. Fig. 1, Taf. VII).

Tafel VII: Fig. 1

Damit Kompensation eintritt, muß nach Maxwell und nach Lorentz sein:

$\varepsilon F=\varepsilon Hu\sin \alpha ,$

(2)	${\frac {u}{v}}=\beta ={\frac {F}{vH\sin \alpha }}.$

Hieraus folgt, daß nur bei ganz bestimmter Geschwindigkeit Kompensation eintreten kann, wenn die Feldstärken und $\alpha$ gegeben sind. Hat man also inhomogene Strahlen und ist der Kondensator sehr enge, so tritt eine Art spektraler Zerlegung ein, indem Strahlen einer bestimmten Geschwindigkeit ganz automatisch den Winkel finden, für den Kompensation eintritt, und der ihnen daher gestattet, den Kondensator zu verlassen und nach der Ablenkung im reinen Magnetfeld auf den Film aufzutreffen.

Zur Anwendung kam ein kreisförmiger Kondensator von 8 cm Durchmesser, dessen Platten aus optisch ebenem, versilbertem Glas bestanden (vgl. Fig. 2a, Taf. VIII). Die Dicke dieser Platten war 5 mm. Vier kleine Quarzplättchen von einer Dicke von 0,25075 mm und einem Durchmesser von 5 mm lagen zwischen den Platten als Distanzstücke. Sie wurden so geordnet, daß sie an den Enden zweier aufeinander senkrecht stehender Durchmesser lagen. Mittels einer Feder wurden die Platten zusammengehalten, ohne daß eine Durchbiegung möglich war. Dies wurde (vgl. Fig. 2a, Taf. VIII) dadurch erreicht, daß der Druck der Feder direkt über den beiden Quarzplättchen ausgeübt wurde. Diese Vorrichtung gestattete auch den Druck gleichmäßig auf beide Plättchen zu verteilen, so daß eine Hebelwirkung ausgeschlossen war.

Tafel VIII: Fig. 2abc

Als Strahlungsquelle diente ein kugelförmiges Körnchen von Radiumfluorid, welches zwischen den Platten im Mittelpunkte in einer kleinen Höhlung lag. Der Durchmesser des Körnchens war 0,5 mm.

Der Kondensator ließ sich vermittelst eines hohlen Konus so in eine zylinderförmige Dose aus Messing mit einem inneren Durchmesser von 16 cm und einer Höhe von 8 cm einsetzen, daß die Zylinderachse genau senkrecht auf den Kondensatorplatten stand und durch das Radiumkörnchen ging. Letzteres lag dann in halber Höhe der Achse (vgl. Fig. 2b, Taf. VIII).

Durch zwei bandförmige Federn ließ sich der photographische Film fest anliegend gegen die Zylinderwand pressen: Als Films wurden Lumièresche Kodakfilms verwandt.

Die Dose konnte durch einen aufgeschliffenen Glasdeckel luftdicht verschlossen werden. Vermittelst eines Messingrohres wurde die Dose an die Luftpumpe, eine Gädepumpe, angeschlossen. Die Gädepumpe hat sich vorzüglich bewährt. Sie wurde beständig im Gange gehalten, um das höchstmögliche Vakuum zu erhalten. Bei einigen Versuchen wurde sie ohne auszusetzen 3 Tage benutzt. Das Vakuum wurde während des Versuches durch Entladungen durch ein angeschmolzenes Geisslerrohr geprüft. Bei allen Versuchen war das Vakuum so hoch, daß die Entladungen zwischen den Zuleitungsdrähten übergingen.

Die Dose wurde in ein 103 cm langes Solenoid von rechteckigem Querschnitt geschoben (Fig. 1, Taf. VII). Jede der beiden Wickelungen des Solenoides hatte etwa 10 Windungen pro Zentimeter. Der Rahmen des Solenoides war hohl und wurde während des Versuches zum Zwecke der Kühlung von Wasser durchströmt. In der Mitte des Solenoides war die Feldstärke durch die Formel

$H=23{,}193\ {\dot {J}}$

bestimmt, wo ${\dot {J}}$ in Ampere gemessen ist. Der Apparat war frei von paramagnetischen Substanzen, wie eine Prüfung vermittelst einer empfindlichen Magnetnadel ergab.

Die Apparate wurden mit großem Geschick und Verständnis von der bekannten Firma M. Wolz in Bonn angefertigt.

Zu der beschriebenen Methode ist historisch noch zu bemerken, daß das Prinzip der gekreuzten Felder zuerst von J. J. Thomson angewandt wurde. Später benutzte Hr. Bestelmeyer dieses Prinzip zur Erzeugung und Ablenkung homogener Strahlen, was einen wesentlichen Fortschritt bedeutete. Von mir wurde dann dieses Thomson-Bestelmeyersche Prinzip zur spektralen Zerlegung der Strahlen verschiedener Geschwindigkeiten weiter entwickelt und zur Untersuchung schief fliegender Strahlen angewandt.

§ 2. Die Hilsmessungen.

A. Das elektrische Feld. Zur Erzeugung des Kondensatorfeldes diente eine Akkumulatorenbatterie von 320 Elementen. Die Spannung wurde vermittelst der bekannten Kompensationsmethode für jede Abteilung von 40 Akkumulatoren einzeln bestimmt und zwar nach jedem Versuch; bei länger dauernden Versuchen auch vorher. Das Westonelement diente als Vergleichselement. Seine Spannung wurde gemäß dem Prüfungsschein der Reichsanstalt als 1,0191 Volt angenommen und bei den unten folgenden Berechnungen verwandt. Bei der Berechnung der in der Physik. Zeitschr. angegebenen $\beta$-Werte wurde die frühere Angabe der Reichsanstalt nämlich 1,020 Volt zugrunde gelegt. Zusammen mit anderen sehr geringfügigen Korrekturen macht dies die $\beta$-Werte um 1,3 Promille kleiner. Bei der Berechnung der Kondensatorspannung wurde berücksichtigt, daß der Widerstand des Kondensators nicht unendlich groß ist und wegen des hohen Vorschaltwiderstandes die Spannung kleiner macht als die Klemmspannung der Akkumulatorenbatterie. Der Vorschaltwiderstand war 660000 Ohm und der Kondensatorwiderstand $10^{9}$ Ohm.

Die Dicke der vier Quarzplättchen, die den Abstand der Kondensatorplatten bestimmen, wurde auf folgende Weise gemessen. Der Wagebalken einer feinen Wage wurde als Hebel benutzt, dessen Drehachse die Schneide war. Das andere Ende ruhte vermittelst einer angekitteten kleinen polierten Stahlkugel auf einer optisch ebenen Platte.

Der Hebelarm, d. h. der Abstand der Schneide von dem Berührungspunkt der Kugel mit der Platte, war 270,7 mm. Auf den Hebel war ein optisch ebener Spiegel in vertikaler Stellung befestigt, in dem sich ein 6149,3 mm entfernter feiner Platindraht spiegelte. Ein feines Wolzsches Kathetometer wurde in demselben Abstand aufgestellt und auf das Bild des Platindrahtes eingestellt. Die Achse des Fernrohres, der Platindraht und die Mitte des Spiegels lagen angenähert in derselben horizontalen Ebene. Es wurde zunächst abgelesen und alsdann zwei Quarzplättchen zwischen Stahlkugel und optische Platte geschoben. Dann wurde wieder abgelesen. Die Differenz betrug für jedes Plattenpaar 22,785 mm. Die Dicke eines Plättchens ist daher:

$d={\frac {22{,}785\times 270{,}7}{2\times 2\times 6149{,}3}}=0{,}25075\ \mathrm {mm.}$

Dieser Wert ist bis auf 1 Promille genau.

B. Das Magnetfeld. Die Intensität des Solenoidfeldes wurde mit derjenigen einer genau ausmeßbaren Standardspule verglichen. Diese Spule bestand aus einem mit einer Lage von 136 Windungen bewickelten Marmorkranze. Der äußere Durchmesser des Marmors war 412,7 mm, die Breite 41,2 mm.

Das magnetische Feld einer solchen Spule ist bekanntlich durch die Formel gegeben:

$H_{\mathrm {Sp.} }={\frac {J\,2\,n\,\pi }{R\left(1+{\dfrac {1}{8}}{\dfrac {b^{2}}{R^{2}}}\right)10}}=4{,}1205\ J,$

wo $b$ die Breite der Spule bedeutet.

Diese Spule wurde so über das Solenoid geschoben, daß die Windungsebenen und die Achsen beider zusammenfielen. Im Innern des Solenoides befand sich genau im Zentrum der Spule ein an einem Quarzfaden aufgehängter empfindlicher kleiner Magnet. Kompensiert man dann die Feldwirkung des Solenoides durch die entgegengesetzte der Spule, so ergibt eine einfache Rechnung die Konstante des Solenoides. Jede der beiden Wickelungen wurde einzeln untersucht und zwar für drei Punkte auf der Achse des Solenoides, für die Mitte $C$ und für zwei Punkte $A$ und $B$, die 8 cm entfernt zu beiden Seiten von $C$ lagen. Für $C$ ergab sich, wie schon erwähnt,

$H=2319{,}3\ {\dot {J}},$

während für $A$ und $B$

$H=(2319{,}3\pm 5){\dot {J}}$

war.

Der Strom wurde von der städtischen Zentrale geliefert und beständig vermittelst eines Siemensschen Präzisionsamperemeters und eines Konstantanwiderstandes reguliert. Die Konstanz des Stromes war im allgemeinen so gut, daß man sicher sein konnte, daß das Magnetfeld auf 1 Promille konstant blieb.

§ 3. Die Versuche.

Die Untersuchung zielte zunächst darauf hin, die Ablenkung schief gegen das Feld fliegender Elektronen zu messen, um die Formel (1) auf ihre Richtigkeit zu prüfen. Wäre nämlich (1) richtig, so müßte statt (2) die Beziehung bestehen:

(3)	$\beta ={\frac {F\left(1-\beta ^{2}\cos ^{2}\alpha \right)}{vH\sin \alpha }}.$

Wählt man daher $F$ und $H$ so, daß $F/vH={\tfrac {1}{2}}$, so wird

(4)	$\beta ={\frac {1}{1+\sin \alpha }}.$

Für $\beta =1$ ist die Ablenkung der kompensierten Strahlen gleich Null. Die Beziehung (4) besagt daher, daß die radiographische Kurve von dem Punkte auf dem Film, der $\alpha =0$ entspricht, anfangen muß. Hingegen folgt aus Gleichung (2), wenn $F/vH={\tfrac {1}{2}}$

(5)	$\beta ={\frac {1}{2\sin \alpha }}.$

Die den kompensierten Strahlen entsprechende Kurve beginnt bei 30°; denn bei diesem Winkel ist $\beta =1$ und daher die Ablenkung Null. Da der Umfang des Films rund 50 cm beträgt, so liegt der Anfang der den kompensierten Strahlen entsprechenden Kurve 4,2 cm von dem durch (4) bestimmten Anfang. Wäre der Schnittpunkt der Kurve mit der durch die $\gamma$-Strahlen erzeugten geraden Linie (vgl. Photographie, Taf. VIII) nur durch die kompensierten Strahlen bedingt, so ließe sich auf den ersten Blick zwischen (4) und (5) entscheiden.

Aber die Theorie der nichtkompensierten Strahlen beweist, daß der Anfang der Kurve von diesen hauptsächlich gebildet wird. Hier ist die Kurve nur nach der konvexen Seite zu scharf begrenzt, während zwischen dieser Begrenzung und der $\gamma$-Linie auch viele Elektronen auftreffen und die Photographie verdunkeln. Hält man sich an die Begrenzungslinie der konvexen Seite, so läßt sich für ihren Schnittpunkt der Ort angeben und dieser entspricht ohne allen Zweifel der Beziehung Gleichung (5).

Sobald als ich dies festgestellt, und damit die Ungültigkeit meines Relativitätsprinzips bewiesen hatte, wandte ich mich der weiteren Aufgabe zu, die Beziehung der elektromagnetischen Masse zu ihrer Geschwindigkeit zu untersuchen und damit zwischen den einzelnen Theorien zu unterscheiden.

Wie ich bereits in meinem vorläufigen Bericht in der Physik. Zeitschrift bemerkt hatte, liefert jede einzelne Kurve die Geschwindigkeitsfunktion der elektromagnetischen Masse. Wenn nun auch die Auswertung einer einzelnen Kurve durchaus zu klaren, eindeutigen Resultaten führen muß, so ist doch die Berechnung so kompliziert, daß die Beweiskraft darunter leiden muß. Da mir daran gelegen ist, in dieser Abhandlung den endgültigen Beweis für die Gültigkeit der Lorentzschen Formel zu erbringen, so beschränke ich mich wiederum auf die Verwertung der maximalen Ablenkungen. Bezeichnet man die transversale Masse mit $m$, den Krümmungsradius der Bahn des Elektrons im Magnetfelde mit $r$, die maximale Ablenkung auf dem Film mit $z$, so gelangt man zu folgenden Beziehungen:

(6)	${\frac {mu^{2}}{r}}=\varepsilon Hu.$

Wie aber eine einfache Rechnung zeigt, ist

(7)	$r={\frac {a^{2}}{2z}}\left(1+{\frac {z^{2}}{a^{2}}}\right),$

wenn $a$ den Abstand des Kondensatorrandes vom Film bezeichnet. Nach Lorentz ist nun

(8)	${\frac {\varepsilon }{m}}={\frac {\varepsilon }{m_{0}}}\left(1-\beta ^{2}\right)^{\tfrac {1}{2}}.$

Dies liefert mit Hilfe der beiden vorstehenden Gleichungen

(9)	${\frac {\varepsilon }{m_{0}}}={\frac {2vz}{\left(a^{2}+z^{2}\right)H}}\tan \operatorname {arc} \sin \beta .$

Hingegen liefert die Abrahamsche Formel für das starre Elektron:

(10)	${\frac {\varepsilon }{m_{0}}}={\frac {2vz}{\left(a^{2}+z^{2}\right)H}}\left\{{\frac {3}{4\beta }}{\frac {2\delta -\tan h2\delta }{\tan h2\delta }}\right\},$

wo $\beta =\tan h\delta$.

Offenbar ist diejenige Theorie die gültige, für die $\varepsilon /m_{0}$ innerhalb der Beobachtungsfehler für beliebige Werte von $\beta$ eine wirkliche Konstante ist.

Die Versuche wurden in der Weise angestellt, daß zuerst in der Dunkelkammer der Film angelegt und dann der Apparat an die Luftpumpe angeschlossen wurde. Es war notwendig, so bald als möglich ein hohes Vakuum zu erzielen, weil das Radiumkorn in Gegenwart von Luftresten stark fluoresziert und dadurch den Film verschleiert. Deshalb war eine Fleusssche Pumpe eingeschaltet, vermittelst welcher das Vorvakuum der Gaedepumpe in einer Minute den normalen Wert erhielt. Dann wurde die Fleusssche Pumpe abgestellt und die Wasserstrahlpumpe versah den Dienst bei der Erhaltung des Vorvakuums. In etwa 20 Min. war volles Röntgenvakuum erreicht und dann wurden die Feldstärken angesetzt. In kurzer Zeit stieg das Vakuum so hoch, daß kein Strom mehr durch das Geisslerrohr ging. Die Dauer der Exposition richtete sich nach dem Geschwindigkeitsbereich der Strahlen. Für einen Bereich von $\beta =1$ bis $\beta =0{,}7$ genügten 4½ Stunden, während für $\beta =1$ bis $\beta =0{,}32$ mindestens 60 Stunden erforderlich waren. Da, wie erwähnt, beständig das magnetische Feld reguliert wurde, so waren die Versuche zum Teil sehr mühsam. Bei abnorm laugen Versuchen war die Gefahr nicht ausgeschlossen, daß die Regulierung im Durchschnitt nicht so exakt war wie bei Versuchen kürzerer Dauer. In der unten angegebenen Tabelle sind solche Versuche unter der Nummer 10 und 11 aufgeführt. Es wurde aus den Ablenkungen dieser beiden Versuche das Mittel genommen.

Tafel VIII: Versuch Nr. 15 (mit Schutzring)

Tafel VIII: Versuch Nr. 7

Nach Beendigung der Exposition wurden die Films entwickelt und dann ausgemessen. Die Ablenkungen waren so genau meßbar, daß man mit bloßem Auge vermittelst eines Normalmaßstabes auf 1/10 mm genau abmessen konnte. Hiervon kann man sich sogar überzeugen, wenn man die reproduzierten Bilder der Kurven ausmißt (vgl. diese). Zum Zweck einer genaueren Ausmessung wurden die Ablenkungen mit einem feinen Kathetometer abgelesen. Einen Vergleich der $z$-Werte, die mit bloßem Auge, und derjenigen, die mit dem Kathetometer gemessen wurden, gestatten die beiden Tabellen.

$z$ in mm
mit dem Auge	mit Kathetometer
06,25 13,50 14,40 16,30 10,15	06,23 13,50 14,45 16,35 10,18

Da die Versuchsmethode gestattet, sämtliche Größen, von denen $\varepsilon /m_{0}$ abhängt, mit großer Genauigkeit zu bestimmen, so müßte sich für die gültige Formel eine haarscharfe Konstanz ergeben. Bevor wir die Formeln anwenden, müssen wir uns aber die Frage vorlegen, ob tatsächlich die Formeln genau der Theorie der Versuchsanordnung entsprechen, und da ergibt eine Prüfung aller in Betracht kommenden Faktoren, daß eine gewisse zugrunde gelegte Annahme nicht vollständig zutrifft. Die Formeln setzen nämlich den idealen Fall voraus, daß das elektrische Feld durch den Rand des Kondensators scharf begrenzt wird. Tatsächlich ist das elektrische Feld nicht auf den Raum zwischen den Platten beschränkt und deshalb ist zu untersuchen, wie die Streuung der Kraftlinien außerhalb des Kondensators die Ablenkung im Magnetfelde beeinflußt.

Die Korrektur für die Randwirkung des Kondensators.

Eine Untersuchung der Frage, in welcher Weise die Streuung der Kraftlinien die Bahn des Elektrons beeinflußt, und welche Korrektur dafür anzubringen ist, führt zu folgenden Ergebnissen.

Fig. 3.

Wir verfolgen die Bahn des Elektrons vom Punkt $O$ aus, der zwischen den Platten und so weit vom Rande entfernt liegt, daß die Feldstärke noch durch den normalen Wert $V/d$ bestimmt ist, wo $V$ die Potentialdifferenz und $d$ den Abstand der Platten bedeutet. Nachdem das Elektron den Punkt $O$ passiert hat, ändert sich etwas seine Bewegungsrichtung, da sich die Kräfte nicht mehr genau kompensieren. Die Zeit, die das Elektron gebraucht, um von $O$ nach $S$ zu gelangen, ist, da die Krümmung der Bahn bis $S$ als sehr gering angenommen ist,

${\frac {u}{OP}}={\frac {u}{x}}.$

Während dieser Zeit erteilt die elektrodynamische Kraft den Impuls

$\varepsilon Hu{\frac {x}{u}}=\varepsilon Hx,$

während die elektrische Kraft den entgegengesetzten Impuls:

${\frac {\varepsilon }{u}}\int \limits _{0}^{x}E\,dx$

erteilt. Der resultierende Impuls ist daher

$M={\frac {\varepsilon }{u}}\int \limits _{0}^{x}E\,dx-\varepsilon Hx.$

Setzt man nun

${\frac {d}{V}}\int \limits _{0}^{x}E\,dx=h,$

so wird

$M={\frac {\varepsilon }{u}}{\frac {Vh}{d}}-H\varepsilon x={\frac {\varepsilon }{u}}{\frac {V}{d}}(h-x).$

Bezeichnet man den Winkel, den die Tangente im Punkte $S$ mit der ursprünglichen Richtung des Elektrons macht, mit $\gamma$, so ist:

$mu\gamma ={\frac {\varepsilon }{u}}{\frac {V}{d}}(h-x),$

(11)	$\gamma ={\frac {\varepsilon }{m}}{\frac {H}{u}}(h-x).$

Hieraus schließt man, daß die Streuung so wirkt, als ob der Radius der Kondensatorplatten um die Strecke $h=p$ vergrößert, und am Rande die elektrische Kraft plötzlich Null geworden wäre.

Es muß daher in den Gleichungen (9) und (10) der wirkliche Abstand $a$ des Kondensatorrandes vom Film durch $a-p$ ersetzt werden, wo $p$ aus der geometrischen Konfiguration des Kondensators zu berechnen ist. So erhält man denn:

(9a)	${\frac {\varepsilon }{m_{0}}}={\frac {2vz}{H\left\{(a-p)^{2}+z^{2}\right\}}}\tan \operatorname {arc} \sin \beta ,$

(10a)

${\frac {\varepsilon }{m_{0}}}={\frac {2vz}{H\left\{(a-p)^{2}+z^{2}\right\}}}\left\{{\frac {3}{4\beta }}{\frac {2\delta -\tan h2\delta }{\tan h2\delta }}\right\}.$

In meiner Veröffentlichung in der Physik. Zeitschrift habe ich den Einfluß von $p$ auf die Größe von $\varepsilon /m_{0}$ unterschätzt, wenn mir auch von vornherein klar war, daß diese Korrektur die Konstanz der $\varepsilon /m_{0}$-Werte nur unwesentlich ändern, also den Nachweis der Gültigkeit des Relativitätsprinzips nicht beeinträchtigen konnte.

Im allgemeinen wird die Konfiguration eines Kondensators nicht so einfach sein, daß man $p$ ohne Hilfsversuche genau angeben könnte. In dem vorliegenden Falle läßt sich aber ein angenäherter Wert von $p$ angeben. Wir betrachten zunächst die Verteilung der Kraftlinien an dem Kondensator ohne den Schutzring. Untersuchungen über diese Frage verdankt man Kirchhoff, Maxwell, J. J. Thomson und J. G. Coffin.^[2]

Der Wert ist hauptsächlich durch die Kraftlinien bedingt, die von den vertikalen Seitenflächen und den horizontalen Außenflächen ausgehen. Letztere waren bis $s=15$ mm vom Rande versilbert. — Bezeichnet man die Dicke der Platten mit $b$ und ihren Abstand mit $d$, so läßt sich aus den Resultaten Coffins, die aber strenge nur für einen geradlinigen Kondensatorrand gelten, mittels des Prinzips der elektrischen Bilder ableiten, daß $p_{1}$, derjenige Teil von $p$, der von den Vertikalflächen herrührt, durch den Ausdruck:

(12)	$p_{1}={\frac {d}{\pi }}\log m$

gegeben ist, wo:

$m={\frac {2b}{d}}+1+{\sqrt {{\frac {2b}{d}}\left({\frac {2b}{d}}+2\right)}}=81{,}52.$

Setzt man ferner, um die Kreisform der Außenflächen zu berücksichtigen, $s'={\tfrac {2}{3}}s=10$ mm, so ist angenähert:

(13)	$p_{2}={\frac {d}{2\pi }}\log \left[1+{\frac {2\pi ms'}{d}}+{\frac {m^{2}}{2}}\log \left(4+{\frac {8\pi ms'}{d}}\right)-m^{2}\log m\right].$

Einen kleinen Beitrag zu $p$ liefert die erhöhte Flächendichte in der Nähe der Kondensatoröffnung:

(14)	$p_{3}={\frac {d}{\pi }}(1-\log 2).$

Man erhält so den Annäherungswert:

(14a)

$p=p_{1}+p_{2}+p_{3}=0{,}77$ mm.

Dieser Wert von $p$ liefert, wenn er nebst den Daten eines Versuches in Gleichung (9a) eingesetzt wird, den Wert von $\varepsilon /m_{0}$. So ergibt Versuch Nr. 13 (vgl. § 4):

${\frac {\varepsilon }{m_{0}}}=\mathbf {1{,}763\times 10^{7}} .$

Dieser Wert ist richtig bis auf ½ Proz.

Bei Verwendung eines Schutzringes wird die Streuung der Kraftlinien, und danach $p$ wesentlich verringert. Eine Wiederholung des Versuches Nr. 13 mit einem Schutzring (vgl. Fig. 2c, Taf. VIII), dessen Abstand vom Kondensator 1 mm, und dessen Spaltbreite 0,9 mm betrug, gestattet $p$ zu berechnen. Setzt man die Versuchsdaten und den Wert $\varepsilon /m_{0}=1{,}763\times 10^{7}$ in Gleichung (9a) ein, so ergibt sich $p=0{,}47$. Der Schutzring beseitigt demnach nur etwa die Hälfte der Streuung. —

Im folgenden Paragraphen ist für jeden Versuch der Wert von $\varepsilon /m_{0}$ unter Zugrundelegung des $p$-Wertes aus Gleichung (14a) berechnet.

§ 4. Die Resultate.

Die Tabelle gibt eine Übersicht über die Resultate.

Nummer des Versuches	$\beta$	$H$	$z$ in mm	${\frac {\varepsilon }{m_{0}}}\times 10^{-7}$ nach Lorentz	${\frac {\varepsilon }{m_{0}}}\times 10^{-7}$ nach Maxwell
10 und 11 8 7 13 15 mit Schutzring 3	,3173 ,3787 ,4281 ,5154 ,5154 ,6870	104,55 115,78 127,37 127,55 127,55 127,55	16,37 14,45 13,50 10,18 10,35 06,23	1,752 1,761 1,760 1,763 – 1,767	1,726 1,733 1,723 1,706 – 1,642

Ein Vergleich der nach der Lorentzschen Formel berechneten $\varepsilon /m_{0}$-Werte mit den nach der Abrahamschen Formel berechneten ergibt die Gültigkeit der Lorentzschen Theorie.

In der Tat ist die Konstanz der $\varepsilon /m_{0}$-Werte eine solche, daß auch die Möglichkeit entfällt, durch Annahme anderer $\beta$-Werte eine Übereinstimmung mit der Abrahamschen Formel zu erzielen. Daß der Wert für $\beta =0{,}317$ etwas abweicht, rührt von der langen Versuchsdauer — 70 Stunden im Durchschnitt — her.

Es ist von Interesse, zu untersuchen, wie die Konstanz sich gestaltet, wenn die Streuung der Kraftlinien vernachlässigt wird, d. h. wenn $p=0$ gesetzt wird. Die Versuche Nr. 8, 7, 13 und 3 liefern dann:

$\beta$	${\frac {\varepsilon }{m_{0}}}\times 10^{-7}$ nach Lorentz	${\frac {\varepsilon }{m_{0}}}\times 10^{-7}$ nach Maxwell
0,3787 0,4281 0,5154 0,6780	1,701 1,699 1,700 1,701	1,675 1,663 1,645 1,580

Aus dieser Zusammenstellung ersieht man, daß der Wert von $\varepsilon /m_{0}$ in weiten Grenzen variieren kann, ohne die Konstanz der nach der Lorentzschen Formel berechneten Werte untereinander wesentlich zu beeinflussen.

Experimentell läßt sich der Wert von $p$ und somit von $\varepsilon /m_{0}$ genau dadurch feststellen, daß man bei den Versuchen mit einem passend modifizierten Apparat den Abstand $a$ des Kondensators vom Film variiert und aus verschiedenen Versuchen nach den Gleichungen (9a) und (10a) $p$ berechnet. Unter meiner Leitung werden im hiesigen Institut von Hrn. stud. math. K. Wolz Versuche in dieser Richtung unternommen.

§ 5. Die Rolle der nicht kompensierten Strahlen.

Oben wurde bereits erwähnt, daß die Schnittpunkte der Kurven mit der $\gamma$-Linie von den innerhalb des Kondensators nicht kompensierten Strahlen herrühren. In der Tat leuchtet ein, daß je mehr die Ablenkung $z$ mit der Breite der Kondensatoröffnung vergleichbar wird, auch Strahlen zur radiographischen Fixierung kommen müssen, die eine größere oder kleinere Geschwindigkeit haben als die kompensierten. Die relative Intensität der Strahlen verschiedener Geschwindigkeiten spielt bei der Erzeugung des Kurvenbildes auch eine wichtige Rolle. Die kompensierten Strahlen erzeugen eine Kurve, deren Breite ¾ mm beträgt, wie sich aus der Berücksichtigung des Plattenabstandes und der Entfernung des Kondensatorrandes vom Film ergibt. Diese Breite ist aber nicht gleich intensiv, denn der mittlere Teil von ¼ mm ist, wie man aus optischer Analogie schließt, bei weitem der intensivste. Die Wirkung der nicht kompensierten Strahlen wird außer von ihrer relativen Intensität davon abhängen, ob ihre Auftreffstelle mit derjenigen der kompensierten Strahlen zusammenfällt oder nicht. Fallen sie damit zusammen, so bleibt die Breite der Kurve unverändert ¾ mm, und es handelt sich nur darum, den Mittelpunkt des Kurvenstreifens festzulegen. Fallen sie nicht zusammen, so ist zu untersuchen, welchen Bereich sie auf dem Film bedecken und in welcher Weise sie die Schwerpunktslinie der Kurve verschieben.

Nun ist wohl zu beachten, daß im allgemeinen die relative Anzahl der nicht kompensierten Elektronen gegenüber den kompensierten eine sehr beschränkte ist und daß daher ihre radiographische Wirkung gering ist, besonders wenn sie sich außerdem über eine größere Fläche verteilen, d. h. wenn die Ablenkung der extremen nicht kompensierten Strahlen sich weit von derjenigen der kompensierten Strahlen entfernt. In zwei Fällen werden die nicht kompensierten Strahlen das Kurvenbild der kompensierten stören. Ist $\beta _{0}$ nahe gleich Eins, so wissen wir, daß die Intensität der Strahlen eine sehr geringe ist und daß daher ihre Wirkung auf den Film verschwindend ist. Hingegen werden die nicht kompensierten Strahlen, deren Geschwindigkeit viel geringer, wenn auch immer noch groß ist, und deren Austritt aus dem Kondensator durch ihre geringe Bahnkrümmung begünstigt wird, in großer Anzahl auf den Film auftreffen und ein Bild erzeugen. In Übereinstimmung mit der Theorie erstreckt sich ihre Ablenkung $z$ über eine große Strecke, so daß ein breites Band entsteht, welches bis zur $\gamma$-Linie reicht und nur auf der konvexen Seite ziemlich scharf begrenzt ist. Diese Erscheinung zeigen sämtliche Aufnahmen in der Nähe des Schnittpunktes der Kurve mit der $\gamma$-Linie. Die nicht kompensierten Strahlen gelangen auch da zur Wirkung, wo sie einem Geschwindigkeitsbereich angehören, der einer erheblich größeren Intensität als derjenigen der normalen Strahlen entspricht, vorausgesetzt daß der Ablenkungsbereich nicht sehr groß ist und daß er nicht zu sehr außerhalb desjenigen der kompensierten Strahlen liegt. In diesem Falle wird sich die Wirkung dann zeigen, daß an der betreffenden Stelle die Kurve verwaschen und breiter als der normale Wert von ¾ mm wird. Ich habe meine Kurvenbilder sorgfältig nach den hier dargelegten Gesichtspunkten geprüft und keine Veranlassung gefunden, eine Korrektur für die Wirkung nicht kompensierter Strahlen anzubringen. Sämtliche Maxima sind wohl definiert und zeigen die normale Kurvenbreite.

In seiner schönen und verdienstvollen Arbeit^[3] hat Hr. Bestelmeyer zum Zwecke der Bestimmung des Kathodenstrahlwertes $\varepsilon /m_{0}$ eine nicht unbedeutende Korrektur wegen der nicht kompensierten Strahlen angebracht und auch später bei der Diskussion meines Vortrages^[4] darauf hingewiesen, daß meine Resultate dadurch vielleicht modifiziert würden. Dies veranlaßt mich, hier näher auf die Theorie dieser Strahlen einzugehen.

Im folgenden beschränke ich mich auf die Untersuchung des Einflusses der nicht kompensierten Strahlen beim Maxiumm.

Fig. 4.

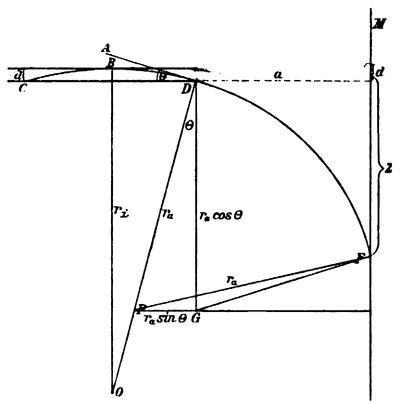
In der Fig. 4 bedeuten die beiden horizontalen Linien mit dem Abstand $d$ die Kondensatorplatten. Bei $C$ liege das Radiumkorn. $CD$ sei der Radius der Kondensatorplatten. Im Abstände $CD=a$ von $D$ befindet sich der Film $M$. Ein Strahl, der nicht kompensiert sei, verlasse das Radiumkorn bei $C$ und beschreibe eine Bahn $CBDF$ mit dem Krümmungsradius $r_{i}$ innerhalb der Platten, und dem Radius $r_{a}$ nach dem Eintritt in das Magnetfeld. Da der Strahl die obere Platte bei $B$ berührt, so ist es ein Strahl größter Krümmung, bei dem die vom Magnetfelde herrührende elektrodynamische Kraft überwiegt. Es muß dann sein:

(15)	${\frac {mu^{2}}{r_{i}}}=\varepsilon (Hu-F).$

Außerhalb des Kondensators gilt dagegen

(16)	${\frac {mu^{2}}{r_{a}}}=\varepsilon Hu.$

Beide Beziehungen liefern

${\frac {r_{a}}{r_{i}}}=1-{\frac {F}{\beta vH}}.$

Bezeichnet man die Geschwindigkeit der kompensierten Strahlen mit $\beta _{0}$, so ist bekanntlich

$\beta _{0}={\frac {F}{vH}}.$

Folglich wird:

(17)	${\frac {r_{a}}{r_{i}}}=1-{\frac {\beta _{0}}{\beta }}$

und vermittelst Gleichung (16)

(18)	${\frac {mv\beta }{r_{i}\,\varepsilon H}}=1-{\frac {\beta _{0}}{\beta }}.$

Nach Lorentz ist:

(19)	${\frac {m}{\varepsilon }}={\frac {m_{0}}{\varepsilon }}\left(1-\beta ^{2}\right)^{-1/2}.$

Die Gleichungen (18) und (19) liefern

(20)	${\frac {\varepsilon }{m_{0}}}={\frac {v}{Hr_{i}}}{\frac {\beta ^{2}}{\left(\beta -\beta _{0}\right){\sqrt {1-\beta ^{2}}}}}.$

Durch die Lösung dieser Gleichung findet man $\beta$; $r_{i}$ ergibt sich aus den Dimensionen des Kondensators. Zieht man dann die Kurve

$y={\frac {\beta ^{2}}{\sqrt {1-\beta ^{2}}}}$

und die Gerade

$y={\frac {\varepsilon }{m_{0}}}{\frac {H}{v}}\left(\pm r_{i}\right)\left(\beta -\beta _{0}\right),$

so liefern die Abszissen der Schnittpunkte der Geraden mit den Kurven die Werte von $\beta$. Der positive Wert von $r_{i}$ entspricht den Strahlen für die $\beta _{0}<\beta$, während der negative den Strahlen entspricht, deren Geschwindigkeit kleiner als die der kompensierten Strahlen ist. Im allgemeinen ergeben sich drei Werte für $\beta$. Ist $\beta$ auf diese Weise gefunden, so setzt man den Wert in Gleichung (17) ein und erhält den Krümmungsradius $r_{a}$ des betreffenden nicht kompensierten Strahles im reinen Magnetfelde. Die nächste Aufgabe besteht nun darin, vermittelst des Wertes von $r_{a}$ und der Dimensionen des Apparates die Ablenkung $z$ zu berechnen. Hierzu dient Fig. 4. Man findet leicht:

$z\mp {\frac {d}{2}}=r_{a}\cos \theta -{\sqrt {r_{a}^{2}-\left(a+r_{a}\sin \theta \right)^{2}}}.$

Da aber nach der Figur $\sin \theta =a/2r_{i}$, und annähernd $\cos \theta =1$, so folgt nach einer leichten Umformung:

$z\mp {\frac {d}{2}}={\frac {2a^{2}\left({\dfrac {1}{2r_{a}}}+{\dfrac {1}{2r_{i}}}\right)}{1+{\sqrt {1-a^{2}\left({\dfrac {1}{r_{a}}}+{\dfrac {1}{2r_{i}}}\right)^{2}}}}}.$

Setzt man:

(21)	${\frac {a}{r_{a}}}+{\frac {a}{2r_{i}}}=\sin \varphi ,$

so findet man:

$z\mp {\frac {d}{2}}=2a\tan {\frac {\varphi }{2}}-{\frac {a^{2}}{2r_{a}}}\sec ^{2}{\frac {\varphi }{2}}.$

Ohne Berücksichtigung der Kleinheit von $\theta$ erhält man die strenge Formel:

(22)	$z\mp {\frac {d}{2}}=a\tan {\frac {\varphi +\theta }{2}}.$

In dem Ausdruck $z\mp d/2$ gilt das negative oder positive Vorzeichen, jenachdem $r_{i}$, also auch $\theta$, positiv oder negativ ist. Mit den Gleichungen (20), (17) und (22) ist alles gegeben, was zur Berechnung der Ablenkung der nichtkompensierten Strahlen erforderlich ist.

Wir wollen nun diese Gleichungen auf einen der Bestelmeyerschen Versuche anwenden. Ich greife den Versuch Nr. 4 heraus. Hier ist $\beta _{0}=0{,}322$. Gleichung (20) liefert durch graphische Lösung $\beta _{1}=0{,}292;\ \beta _{2}=0{,}374$ als die Grenzwerte der nichtkompensierten Strahlen. Mit diesen Werten wird nach Gleichung (17)

$r_{a_{1}}=9{,}93;\quad r_{a_{2}}=13{,}2$, da $r_{i}=96$ cm.

Dann ist

$\varphi _{1}=39^{\circ }25';\quad \theta _{1}=-1^{\circ }59';\quad {\frac {\varphi _{1}+\theta _{1}}{2}}=18^{\circ }43'$

und daher

$z_{1}=6{,}65\tan 18^{\circ }43+{\frac {d}{2}}=22{,}24\ \mathrm {mm} ,$

während die Ablenkung $z_{2}$ der Grenzstrahlen für $\beta _{2}$ sich wie folgt berechnet:

$\varphi _{2}=32^{\circ }40';\quad \theta _{2}=1^{\circ }59';\quad {\frac {\varphi _{2}+\theta _{2}}{2}}=17^{\circ }19';$

$z_{2}=20{,}73+0{,}29=21{,}02\ \mathrm {mm} .$

Zunächst ergibt sich der Geschwindigkeitsbereich der extremen Strahlen als 91 - 114 Proz. der kompensierten Strahlen. Die Ablenkung $z$ der letzteren ist

${\begin{array}{l}z=a\tan {\dfrac {\varphi }{2}}=6{,}65\times 0{,}333\ \mathrm {cm} ,\\\\z=22{,}15\ \mathrm {mm} .\end{array}}$

Von diesem Wert weicht die Ablenkung der langsameren Strahlen um $+0{,}09$ mm ab, während die der größeren Geschwindigkeit entsprechende Ablenkung um $-1{,}13$ mm abweicht. Letztere Strahlen können, weil sie sich über eine so große Fläche ausbreiten, die radiographische Fixierung der kompensierten Strahlen nicht stören, und was die langsameren Strahlen betrifft, so ist ihre Wirkung die, daß die obere Begrenzungslinie der Kurve wenig mehr als 1/10 mm von der Begrenzungslinie der von den kompensierten Strahlen erzeugten Kurve abweicht^{[WS 1]}. Selbst wenn diese langsameren Strahlen mit bedeutend größerer Intensität erzeugt würden, könnten sie den Wert von $\varepsilon /m_{0}$ höchstens um ½ Proz. ändern.

Es ist noch zu bemerken, daß Hr. Bestelmeyer nicht $z=22{,}15$ mm gemessen hat, wie man aus seinen übrigen Daten schließen würde, sondern 22,65. Der richtig berechnete Wert für $\varepsilon /m_{0}$ würde demgemäß größer werden, etwa $1{,}76\times 10^{7}$, abgesehen von einer kleinen Korrektur für die Randwirkung seines Kondensators, und für die Vertikalkomponente der Geschwindigkeit.

Nachdem ich, wie ich glaube, den Nachweis der Gültigkeit des Lorentz-Einsteinschen Relativitätsprinzips erbracht habe, möchte ich in ganz kurzen Zügen von dem neugewonnenen Standpunkte aus die Wandlungen beleuchten, die die Theorie des Elektromagnetismus seit Maxwell erfahren hat. Es wird sich so erweisen, daß die Geschichte des Elektromagnetismus die erkenntnistheoretische Geschichte des Äthers ist.

Nach der Auffassung Maxwells war der Äther der große Vermittler und Träger aller elektromagnetischen Erscheinungen und an dieses Bild knüpfen sich die glänzendsten Entdeckungen der Neuzeit. Bei dem weiteren Ausbau der Theorie lehnten sich die Physiker immer wieder an dieses Bild an, besonders auch in ihrer Anwendung auf die Elektrodynamik bewegter Körper. Bei der Behandlung dieses wichtigen Problems trat die Frage, ob der Äther sich mit der Materie bewegt oder nicht, in den Vordergrund. In dieser Fragestellung dokumentiert sich ein Dualismus von Äther und Materie. Dem Äther wird die Rolle einer Quasimaterie zuerteilt.

Auf der Grundlage des ruhenden Äthers baute Lorentz seine ältere Elektronentheorie auf. In diesem Werke vollzieht sich bereits eine Abschwenkung von der Hauptidee Maxwells, indem den aus Elementarquanten zusammengesetzten Ladungen, die bei Maxwell lediglich singuläre Stellen in der Verteilung des elektrischen Vektors darstellen, bei den elektromagnetischen Erscheinungen die wichtigere Rolle zuerteilt wird. So entstand die Elektronentheorie. Der von Lorentz übernommene Dualismus von Äther und Materie zeitigte dann Schwierigkeiten, deren Überwindung einen so fundamentalen Fortschritt im Gefolge haben sollte. Es ist ja bekannt, daß die Annahme einer Relativbewegung von Äther und Materie zu einer theoretischen Beeinflussung der terrestrischen Optik durch die jährliche Bewegung der Erde führt. Das Experiment widerlegte diese Konsequenz. Damit war die Notwendigkeit einer Umgestaltung der Maxwell-Lorentzschen Theorie gegeben.

Es ist nun bedeutsam, daß bei allen dahin zielenden Versuchen sich die Überzeugung kund gab, daß die Maxwellschen Gleichungen den wahren Ausdruck der elektromagnetischen Gesetzmäßigkeiten darstellten und daß nur die richtige Deutung dieser Gleichungen zu suchen sei. Es ist das große Verdienst von Lorentz, den Nachweis erbracht zu haben, daß durch gewisse Transformationen der unabhängigen Variabeln, bei welchen die Form der Gleichungen erhalten bleibt, eine vollständige Übereinstimmung zwischen Theorie und Erfahrung erzielt wird, und daß vor allem der Einfluß translatorischer Bewegung auf die in einem System stattfindenden Vorgänge verschwindet. Lorentz ist damit der Begründer des Relativitätsprinzips geworden, wenn er auch noch an der Hypothese einer absoluten Bewegung, d. h. einer Bewegung der Materie relativ zum Äther festhält.

Letztere Hypothese gibt zu schwerwiegenden Bedenken Anlaß; sie setzt voraus, daß sich in einem strukturlosen homogenen unbegrenzten Medium ein Bezugssystem festlegen lasse. Eine derartige Festlegung ist mathematisch undenkbar.

Frei von diesen — allerdings nur formalen — Bedenken ist die Einsteinsche Fassung des Relativitätsprinzips. Sein Verfahren ist rein phänomenologisch. Die Problemstellung ist diese: Gegeben die Maxwellschen Gleichungen und die experimentelle Tatsache, daß elektromagnetische Erscheinungen durch eine gleichförmige Translation nicht beeinflußt werden. Welche Transformation ist mit den unabhängigen Variabeln vorzunehmen? Die erwähnte Nichtbeeinflussung läßt sich in dieser Form ausdrücken: Ordnet man in dem betrachteten System einem Raumpunkt einen Zeitwert zu, so erfolgt die Übermittelung eines elektromagnetischen Signals zwischen zwei beliebigen Punkten stets mit derselben Geschwindigkeit $v$, der Lichtgeschwindigkeit, unabhängig von dem gleichförmigen Bewegungszustand des Systems. Bezeichnet man daher den Zeitwert eines Ereignisses im Punkte $A$ mit $t_{A}$ und in dem in der Entfernung $r$ liegenden Punkte $B$ mit $t_{B}$, so ist

$r=v\left(t_{B}-t_{A}\right).$

Alles andere folgt auf rein formalem Wege. Um zunächst die Raumkoordinaten mit der gegebenen Zeitdefinition in Einklang zu bringen, betrachtet Einstein zwei Systeme $S$ und $S'$, die mit der Geschwindigkeit $u$ in gleichförmiger Relativbewegung zueinander begriffen sind.

Ist dann ein Punktereignis als zu dem System $S$ gehörig durch die Variabeln $x,\ y,\ z,\ t$ bestimmt, und als zu dem System $S'$ gehörig durch $x',\ y',\ z',\ t'$, dann wird der obigen Zeitdefinition genügt, wenn die Beziehungen bestehen:

${\begin{array}{l}t'=\alpha \left(t-{\dfrac {u}{v^{2}}}x\right),\\\\x'=\alpha (x-ut),\\\\y'=y,\\\\z'=z,\end{array}}$

wo

$\alpha ={\frac {1}{\sqrt {1-{\dfrac {u^{2}}{v^{2}}}}}}.$

Die Folgerungen, die sich aus der Einsteinschen Theorie für das Experiment und die Erfahrung ergeben, sind mit denjenigen der Lorentzschen Theorie identisch. Da aber, wie erwähnt, die Einsteinsche Ableitung sich auf keine physikalischen Hypothesen stützt, und vor allem die Ätherhypothese in ihrem dualistischen Gewande vermeidet, so ist dadurch die Möglichkeit gegeben, ein ganz neues Bild von dem Wesen der Materie und des Äthers und ihren wechselseitigen Beziehungen zu konstruieren.

Dieses Bild wird sich nur auf monistischer Grundlage entwerfen lassen, auf der Annahme einer Wesensgleichheit von Äther und Materie. Vielleicht gelingt es in Zukunft, die Schwierigkeiten zu überwinden, die sich bisher der Ätherwirbeltheorie entgegengestellt haben. In diesen Wandlungen betätigt sich die Lebenskraft der Ätherhypothese. Nachdem sie den Angelpunkt in einer glänzenden Epoche des Elektromagnetismus gebildet hatte, sank sie allmählich zu geringerer Bedeutung, ja zum Verschwinden herab, um von neuem zu erhöhter Bedeutung zu steigen. —

Es drängt sich nunmehr die Frage auf: in welchem Lichte erscheinen gewisse Probleme, deren Lösung auf Grund der früheren Theorien unbefriedigend war? Wie bereits bemerkt wurde, werden unsere bisherigen Erfahrungen durch das Relativitätsprinzip vollständig erklärt. Formale Bedenken, die gegen die frühere Form der Maxwellschen Theorie geltend gemacht wurde, nehmen aber zum Teil nur ein anderes Gewand an. Ein derartiges Bedenken richtet sich gegen die Nichterfüllung des Prinzips der Gleichheit von Aktion und Reaktion. Bekanntlich trat diese Schwierigkeit der älteren Lorentzschen Theorie in doppelter Gestalt auf. Erstlich übte ein ruhender Körper auf einen bewegten eine andere Kraft aus als umgekehrt. Dann ferner traten unter gewissen Umständen Kräfte im Äther auf, welche diesen, entgegen der Grundannahme, selbst in Bewegung setzen würden.

Der erstere Einwand verliert viel von seinem Gewicht durch die Erwägung, daß zwar je nach dem Standpunkt des Beobachters auf einem der beiden Systeme der eine oder der andere Körper die größere Kraftwirkung erfährt, daß aber diese Wechselwirkung von einem passend gewählten dritten System aus betrachtet ganz unabhängig davon ist, ob der eine oder der andere der beiden Körper als ruhend angenommen wird.

Der andere Einwand läßt sich, wie ich zeigen möchte, durch eine besondere Hypothese über die Lokalisierung der Angriffspunkte der auf elektromagnetische Massen wirkenden mechanischen Kräfte beseitigen. Transformiert man nämlich den Ausdruck für die mechanische Kraft in der von Lorentz angegebenen Weise, so erhält man bekanntlich eine Flächenkraft und eine an den Volumenelementen des Raumes angreifende Kraft:

(1)	$\int {\mathfrak {F}}\varrho d\tau =\int {\mathfrak {G}}df+{\frac {1}{4\pi vdt}}\int [{\mathfrak {HE}}]d\tau .$

In vielen Fällen verschwindet der erste Term, wenn die begrenzende Fläche ins Unendliche gerückt wird und die ganze Kraft ${\mathfrak {K}}$ ist dann gleich der zeitlichen Änderung der Bewegungsgröße:

(2)	${\mathfrak {K}}={\frac {d}{dt}}{\frac {1}{4\pi v}}\int [{\mathfrak {HE}}]d\tau .$

Das Objekt der Kraft ist die elektromagnetische Masse, die sich nach mechanischen Prinzipien aus der durch Gleichung (2) angegebenen Bewegungsgröße ableiten läßt.

Wir führen nun die Hypothese ein, daß die elektromagnetische Masse, die sich als Tensortripel ergibt:

$m=\left(s^{-3/2},\ s^{-1/2},\ s^{-1/2}\right)m_{0},$

wo $s=1-\left(u^{2}/v^{2}\right)$ ist, tatsächlich so verteilt ist, wie dies dem Volumintegral (2) entspricht und daß die mechanische Kraft an diesen Massenelementen angreift.

Wie ich bereits l. c. p. 456 bemerkt hatte, läßt sich der Satz von der Erhaltung des Schwerpunktes auch in strahlenden Systemen aufrecht erhalten, wenn man mit dem Poyntingschen Strahlvektor eine Ausstrahlung von träger Masse verknüpft. Dem Poyntingschen Vektor entspricht bekanntlich eine ihm proportionale Bewegungsgröße und diese kompensiert die Änderung der Bewegungsgröße ${\mathfrak {M}}$ des strahlenden Körpers, so daß die Beziehung besteht:

$\delta {\mathfrak {M}}+{\frac {1}{4\pi v}}\int [{\mathfrak {EH}}]d\tau =0.$

Die Auswertung des Zahlenwertes des Integrals liefert pro Volumeneinheit $E/v$, wenn man mit $E$ die im durchstrahlten Raum pro Volumeinheit enthaltene elektromagnetische Energie bezeichnet. Dies bedeutet, daß der „Strahlungsmasse“ pro Volumeinheit der Wert $E/v^{2}$ zukommt.

Mir scheint die Erweiterung des Begriffes der Masse von weittragender Bedeutung, denn sie führt in ihren letzten Konsequenzen zu der Auffassung der ponderablen Materie als einer Form des Äthers, sie führt zur Entmaterialisierung der Materie.

(Eingegangen 21. Dezember 1908.)

---

1. A. H. Bucherer, Phil. Mag. April 1907. p. 413.
2. J. G. Coffin, Proceed. of the Amer. Acad. 39. Nr. 19. 1903.
3. A. Bestelmeyer, Ann. d. Phys. 22. p. 429. 1907.
4. A. H. Bucherer, Physik. Zeitschr. 9. p. 760. 1908.

Anmerkungen (Wikisource)

1. Vorlage: ahweicht