Konstanz der Lichtgeschwindigkeit
Wenn eine Lichtquelle eine Geschwindigkeit u hat, sagen wir in der Richtung der positiven X–Achse, so ist nach der Theorie von Ritz die Geschwindigkeit des ausgesandten Lichtes in derselben Richtung C+u, wo C die Geschwindigkeit des von einer ruhenden Quelle ausgesandten Lichtes ist. In anderen Theorien (Lorentz, Einstein) ist die Lichtgeschwindigkeit immer konstant gleich C, unabhängig von der Bewegung der Quelle. Nun ist sehr einfach einzusehen, daß die von Ritz angenommene Abhängigkeit der Lichtgeschwindigkeit von der Bewegung der Quelle absolut unzulässig ist.
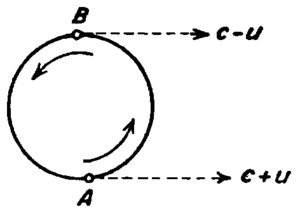
Man denke sich einen Doppelstern, und einen Beobachter in einer großen Entfernung Δ in die Bahnebene. Das vom Stern im Punkte A (siehe Figur) ausgesandte Licht wird gemäß der Theorie von Ritz beobachtet nach einer Zeit Δ/(C+u), das von B ausgesandte Licht nach einer Zeit Δ/(C–u). Nennen wir T die halbe Umlaufszeit des Sterns (dessen Bahn einfachheitshalber als kreisförmig gedacht ist), so ist das Zeitintervall zwischen den beiden Beobachtungen . Geht der Stern in der zweiten Hälfte seiner Periode von B nach A, so ist das beobachtete Zeitintervall . In der gewöhnlichen Theorie sind beide Intervalle gleich T. Wenn nun von derselben Größenordnung ist wie T, so würde es, wenn die Ritzsche Theorie wahr wäre, unmöglich sein, die Beobachtungen mit den Keplerschen Gesetzen in Einklang zu bringen. Bei allen spektroskopischen Doppelsternen ist nun in der Tat nicht nur von derselben Größenordnung wie T, sondern wahrscheinlich in den meisten Fällen sogar viel größer. Nimmt man z. B. u = 100 , T = 8 Tage, = 33 Jahre (d. i. eine Parallaxe von 0,1″), so hat man annähernd . All diese Größen sind von einer Ordnung, die bei den bestbekannten spektroskopischen Doppelsternen sehr häufig ist. (Die meisten Parallaxen werden wohl kleiner als 0,1″ sein.)
Die Existenz der spektroskopischen Doppelsterne und der Umstand, daß in weitaus den meisten Fällen die beobachtete Radialgeschwindigkeit vollständig durch die Keplersche Bewegung repräsentiert wird, ist also ein kräftiger Beweis für die Konstanz der Lichtgeschwindigkeit. Es mag noch daran erinnert werden, daß in vielen Fällen die aus den Radialgeschwindigkeiten abgeleitete Bahnbewegung durch visuelle Beobachtungen (wie bei δ Equulei, ζ Herculis usw.) oder durch die Beobachtung der Verfinsterung der einen Komponente des Doppelsternes durch die andere (wie bei den Algol-variabeln) bestätigt wird.
Leiden, Februar 1913.






