Der Sagnac-Effekt: ein Experimentum crucis zugunsten des Äthers?
1. Der gemeinsame Grundgedanke derjenigen wirklich ausgeführten oder ausgeführt gedachten optischen Experimente, welche die Existenz oder Nichtexistenz des „Äthers“ entscheiden sollen, ist der folgende:
Gibt es einen Äther, so müssen die optischen Vorgänge in allen Systemen, die sich relativ zum Äther bewegen, abweichend verlaufen; insbesondere muß in allen derartigen Systemen ein anderer Wert der Lichtgeschwindigkeit gemessen werden als der Standardwert .
Den zu erwartenden Betrag dieser Änderung bestimmt, abgesehen von der Bewegungsrichtung, die Größe der Relativgeschwindigkeit des Systems zum Äther (oder, umgekehrt betrachtet, die Geschwindigkeit des relativen „Ätherstromes“ oder „Ätherwindes“).
Die größten Relativgeschwindigkeiten, die man bisher hat in Rechnung setzen können, sind von der Größenordnung 30 km/sec gewesen, der zu erwartende Effekt demzufolge durch das Verhältnis = etwa gegeben.
Indessen hat man bisher die Überzeugung gehabt, daß der Effekt von dieser Größenordnung, also der ersten, sich der Messung entziehen müsse, hauptsächlich, weil er Beobachtungen an zwei verschiedenen Punkten des Systems nötig mache.
So gelangte die Entscheidung an die Effekte zweiter Ordnung (also im günstigsten Fall = etwa ). Schon Maxwell hatte nachgewiesen, daß Glieder zweiter Ordnung durch Messung an einem und demselben Punkt festgestellt werden können müßten; das Experimentum crucis ist der Versuch von Michelson geworden.
Das negative Ergebnis dieses Versuches ist es hauptsächlich gewesen, was viele Physiker, besonders die Anhänger des neueren Relativitätsprinzips, endgültig dazu geführt hat, auf den Äther zu verzichten.
2. Nun hat neuerdings Herr Sagnac[1] einen neuen optischen Effekt zwecks Entscheidung der Ätherfrage angegeben.
Dieser neue Effekt ist bemerkenswerterweise von der ersten Ordnung; trotzdem finden alle Messungen an einem und demselben Punkt des Systems statt.
Der Effekt läßt sich daher auch bei nur kleinen Translationsgeschwindigkeiten sehr wohl mittels Interferenzerscheinungen beobachten, und Herr Sagnac hat das auch getan.

Der Effekt hat sich in der Tat gezeigt, Größenordnung und Sinn der Verschiebung stimmt, und überdies stehen die beobachteten Streifenverschiebungen sogar zahlenmäßig in auffallend guter Übereinstimmung mit den berechneten.
Herr Sagnac zieht daher aus Theorie und Experiment den Schluß:[2] Die Streifenverschiebung mißt die Relativgeschwindigkeit des Systems zum Äther (oder den relativen Ätherwind, vent relatif de l’éther), beweist also die Existenz des Äthers.
3. Die Arbeit von Herrn Sagnac ist demnach von sehr großer Wichtigkeit.
Ich denke nun nicht daran, den experimentellen Teil der Arbeit im geringsten in Zweifel zu ziehen, im Gegenteil halte ich die Methode selber noch in verschiedenen Richtungen für entwickelungsfähig.
Dagegen erscheinen mir die theoretischen Grundlagen und demgemäß auch die Schlußfolgerungen nicht mit Notwendigkeit die von Herrn Sagnac gegebene Deutung zu erfordern.
4. Ich gestatte mir, den Grundgedanken der Versuchsanordnung in einer etwas schematisierten Form wiederzugeben, mit dem Bemerken, daß die Sache dadurch nicht geändert wird.
Gegeben ist (Fig. 1) ein auf der Innenseite spiegelnder Kreis mit dem Halbmesser .
An einem Randpunkt wird ein Lichtstrahl geteilt, der eine Teil geht rechts herum, der andere Teil links herum.
 |
 |
Beide Teile beschreiben eben dasselbe, mit einmaligem Umlauf geschlossene Polygon (in der Fig. 1 ein Achteck).
Bezeichnet den Umfang des Polygons, dann ist dasselbe also der Lichtweg für beide Strahlen; die Umlaufzeit ist:
beide Strahlen kommen gleichzeitig wieder in an.
Jetzt denke man dem Beobachtungspunkt eine Translationsgeschwindigkeit erteilt, und zwar soll das geschehen, indem der Kreis mit der Tourenzahl gedreht wird, es soll also sein:
Ebensowohl[3] kann man sich auch den Punkt und den ganzen Kreis dauernd in Ruhe gehalten denken, es herrscht dann an der Stelle wie an jedem Randpunkt des Kreises ein entgegengesetzt gerichteter Ätherwind (vent relatif de l’éther) mit demselben Absolutbetrag
| 1) |
der relativen Äthergeschwindigkeit.
Die gedachte Drehung des Systems erfolge links () herum,
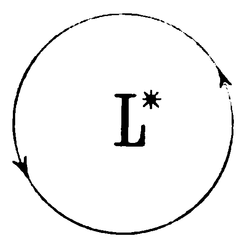
dann geht der relative Ätherwind im Verhältnis zu dem ruhend gedachten System rechts () herum.

Von den beiden mit und bezeichneten, rechts und links herumlaufenden Lichtstrahlen wird daher der eine, nämlich der Strahl , zunächst schneller von weg, dann in gleichem Maße schneller um den ganzen Kreis herum und ebenso schneller wieder zu dem Punkt hingeführt, der andere, , wird in gleicher Weise zurückgehalten. —
Wenn irgend eine Welle durch eine relative Strömung des wellentragenden Mediums schneller befördert oder zurückgehalten wird, dann ist bekanntlich in erster Annäherung die Zeit der Verfrühung oder Verspätung gegenüber der bei der Standardgeschwindigkeit gebrauchten Normalzeit bestimmt durch
falls die Richtungen von und genau zusammenfallen bzw. genau entgegengesetzt sind; statt der Zeit kann man auch die (scheinbare) Wegverkürzung oder -verlängerung einführen, dann ist im Verhältnis zum Normalweg („wirklichen“ Weg) bestimmt durch:
| 2) |
und die Phasenänderung ist bei der Wellenlänge gegeben durch:
| 3) |
Diese Formel ist auch in unserem Fall anzuwenden, nur ist zu berücksichtigen, daß die Richtung der Translationsgeschwindigkeit (Tangente)

und des Lichtes (Polygonseite) nicht zusammenfallen, es ist also, wie sich aus Fig. 2 leicht ergibt, statt einzusetzen:
wenn den zu einer Polygonseite gehörigen Zentriwinkel bezeichnet.
Führt man diesen Wert ein, so wird die Phasendifferenz , die die Strahlen und infolge des relativen Ätherstromes gegeneinander erfahren:
| 4) |
Schließlich kann man für die Geschwindigkeit des relativen Ätherstromes noch den Wert 1) einsetzen mit Tourenzahl und Kreisradius , dann ergibt sich:
| 5) |
Herr Sagnac läßt zwecks Messung den Apparat sich erst in dem einen und dann in dem anderen Sinn herumdrehen, er mißt also , und seine Endformel[4] lautet demnach:
| 6) |
Nach dieser Formel 6) berechnet Herr Sagnac die zu erwartende Streifenverschiebung; daß der Effekt in der Tat von der ersten Ordnung ist, zeigt die Gestalt 4) derselben Formel.
Wie gesagt, stimmen dann die beobachteten Werte mit den berechneten durchaus befriedigend überein.
Der Kreisdurchmesser beträgt dabei 50 cm; die Tourenzahl ist von der Größenordnung 1 oder 2 Umdrehungen pro Sekunde; die Interferenzbilder werden auf photographischem Wege festgehalten; photographische Platte, Lichtquelle usw. nehmen an der Rotation teil.
5. Es fragt sich nun, ob Herrn Sagnacs Schlußfolgerung: der Effekt entscheidet die Alternative „Äther oder Relativitätsprinzip“, und zwar gegen das Relativitätsprinzip und für den Äther, zwingend ist.[5]
Mir scheint die folgende Deutung möglich zu sein:
a) Daß der Effekt zustande kommt, liegt nicht an der Translationsgeschwindigkeit des Beobachtungspunktes , sondern an der Rotationsbewegung des ganzen Systems (und damit natürlich auch des Punktes ).
b) Weil der Effekt aber durch Rotation bedingt wird, ist er nicht nur vom Standpunkt der Äthertheorien, sondern ebensowohl auch vom Anti-Ätherstandpunkt ein notwendiges Postulat.
c) Der Effekt beweist also die Existenz des Äthers nicht.
6. Die Richtigkeit der Behauptung a) ergibt sich ohne weiteres, indem man dem ganzen System anstatt des Rotationsvorganges irgend eine geradlinig gleichförmige Translation erteilt denkt.[6] Der Effekt bleibt dann aus.
Von dem leicht allgemein zu führenden Beweis sehe ich ab, weil mir eine Bemerkung von Herrn Sagnac selber in einer älteren

Arbeit[7] dafür zu sprechen scheint, daß in diesem Punkt seine Ansicht meiner Anschauung nicht widerspricht.
7. Auch bei der Behauptung b) wird eine schematisierende Andeutung genügen.
Zunächst ergibt sich leicht: Das Auftreten des Effektes ist auch dann ein notwendiges Postulat, wenn man den Vorgang bei der Rotation nicht in der Auffassung des § 4 (rotierende Scheibe, ruhend gedacht, ringsherum relativer Ätherwind), sondern vom Standpunkt des vorher ruhenden Systems betrachtet (Äther „ruhend“, Scheibe dagegen rotierend).
Zur Veranschaulichung diene Fig. 3: Das Polygon sei beim Ruhevorgang ein geschlossenes Quadrat, für den Lichtstrahl und für den Lichtstrahl ; sei der Bogen , den der Punkt während des normalen Lichtumlaufes beschreibt, wenn der Apparat wie oben rotiert (Pfeilrichtung ). Dann tritt bei dieser Auffassung für den Lichtweg eine reale Verkürzung ein, für den Lichtweg eine reale Verlängerung, denn die Lichtwege sind in derselben Annäherung wie oben und . Rechnet man die Phasenverschiebung aus, so ergibt sich derselbe Betrag wie oben (Formel 6).
Weiterhin ergibt sich in bekannter Weise vom Standpunkt der Anti-Äthertheorie (Relativitätsprinzip) das gleiche,[8] man hat nur für Äther das Wort „ein Inertialsystem“ zu setzen.
Der Effekt muß daher auch vom Standpunkt des Relativitätsprinzips gefordert werden, und zwar ist der Grund für sein Zustandekommen, daß der Apparat relativ zu einem „Inertialsystem“ rotiert, und daß dadurch, von dem Inertialsystem betrachtet, objektive Verkürzungen bzw. Verlängerungen erster Ordnung bei den Gesamtlichtwegen eintreten.
Dieselben Folgerungen gelten dann natürlich vom Relativitätsstandpunkt aus für jedes beliebige Inertialsystem.[9]
8. Infolgedessen ist auch die Behauptung c) richtig: Der Effekt beweist die Existenz des Äthers nicht.
Der rotierende relative Ätherwind des § 4 darf vom Anti-Ätherstandpunkt aus überhaupt nicht herangezogen werden, das rotierende System ist im Sinne der Relativitätsterminologie überhaupt kein „berechtigtes“ System, d. h. man kann natürlich niemandem verbieten, den tatsächlich eintretenden Effekt durch einen „relativen Ätherwind“ zu illustrieren, aber das ist dann eben vom Relativitätsstandpunkt nur ein Bild, etwa wie: die Sonne geht auf.
Für die Entscheidung: Äther oder Nicht-Äther? fallen nach relativitätstheoretischer Auffassung sämtliche Rotationssysteme überhaupt aus. Die Existenz des Äthers ist bewiesen, sobald bewiesen wird: ein Inertialsystem ist vor den anderen Inertialsystemen ausgezeichnet; sobald man also beim Vergleich von Inertialsystemen untereinander einen „Effekt“ der besprochenen oder einer ähnlichen Art findet. Vor Rotationssystemen dagegen ist gerade vom Relativitätsstandpunkt aus jedes Inertialsystem ausgezeichnet, und umgekehrt; beim Vergleich von Inertial- mit Rotationssystemen oder von Rotationssystemen untereinander kann und muß man daher immer „Effekte“ erhalten.
Braunschweig, Technische Hochschule, im Januar 1914.
- ↑ G. Sagnac, L’éther lumineux démontré par l’effet du vent relatif d’éther, C. R. 157, 708, 27. Oktober 1913; Sur la preuve de la réalité de l’éther lumineux, ebenda S. 1410, 22. Dezember 1913.
- ↑ A. a. O., S. 710 u. 1413.
- ↑ G. Sagnac, a. a. O., S. 709 u. 1411.
- ↑ A. a. O., S. 710 u. 1412.
- ↑ Nur auf diese Alternative gehe ich im folgenden ein. Bezüglich einer anderen wichtigen Alternative, nämlich „Emissions- oder Nicht-Emissionstheorie“ scheint mir der Effekt sehr wohl als Experimentum crucis herangezogen werden zu können (gegen die Emissionstheorien), er ist dann ein sehr wertvolles terrestrisches Gegenstück zu den bekannten astronomischen Beweisen.
- ↑ Z. B. diejenige (fortwährend wechselnde), welche der Punkt allein in jedem Augenblick angenähert ausführt (Richtung Kreistangente, Geschwindigkeit das oben angegebene ).
- ↑ G. Sagnac, Congrès International de Radiologie et d’Électricité, S. 221, Brüssel 1911.
- ↑ Es ist zu berücksichtigen, daß die jeweilige Translationsgeschwindigkeit der Spiegel in der Spiegelebene liegt. Von einem eventuellen Einfluß einer etwaigen zeitlichen Dauer des Reflexionsvorgangs selber ist dabei natürlich abgesehen (wie das auch Herr Sagnac tut). Auch liegt meinen Folgerungen die Annahme zugrunde, daß der mehrfach umstrittene Vorgang der Rotation eines festen Systems für das Relativitätsprinzip als solcher keine Schwierigkeit einschließt.
- ↑ Z. B. auch für dasjenige (fortwährend wechselnde), in welchem sich der Punkt in jedem Augenblick gerade befindet (Richtung Kreistangente, Geschwindigkeit relativ zu dem „Ruh“-Inertialsystem das obige ).

















































