MKL1888:Elektrische Schwingungen

Elektrische Schwingungen, wie sie bei der oszillierenden Entladung eines Kondensators entstehen, pflanzen sich nach der Entdeckung von Hertz (s. Induktion, Bd. 17, S. 451) in der Luft oder andern diëlektrischen Substanzen (Nichtleitern der Elektrizität^{[WS 1]} als elektrische Wellen oder als „Strahlen elektrischer Kraft“ mit einer Geschwindigkeit fort, welche derjenigen des Lichtes nahezu gleich ist. Auch in anderer Hinsicht verhalten sich die elektrischen Strahlen wie Lichtstrahlen; sie werden an Spiegeln zurückgeworfen, durch Prismen gebrochen, sie zeigen Interferenz- und Polarisationserscheinungen. Erregt man z. B. e. S. in der Brennlinie eines cylindrischen Hohlspiegels aus Zinkblech, dem ein zweiter solcher Hohlspiegel gerade gegenübersteht, so werden die an dem ersten Spiegel unter sich parallel zurückgeworfenen Strahlen in der Brennlinie des zweiten wieder gesammelt. Es entstehen dann in einem hier aufgestellten Leiter wieder e. S., welche sich dadurch verraten, daß an einer Unterbrechungsstelle dieses „sekundären Leiters“ zwischen einer Kugel und einer Spitze kleine Funken überspringen. Diese Fünkchen sind aber so schwach, daß sie nur ganz in der Nähe und mit Hilfe einer Lupe beobachtet werden können. Man kann aber ihr Auftreten auch einem größern Zuschauerkreis auf folgende von Boltzmann angegebene Weise wahrnehmbar machen: Man verbindet die Kugel mit einem Goldblattelektroskop, die Spitze mit dem einen Pol einer passenden galvanischen Batterie oder einer Zambonischen Säule, deren anderer Pol zur Erde abgeleitet ist, oder auch mit dem Knopf einer schwach geladenen Leidener Flasche. Solange keine Fünkchen übergehen, bleibt das Elektroskop ungeladen; die Fünkchen aber bilden sofort nach ihrem Erscheinen eine leitende Brücke zwischen Kugel und Spitze und bringen das Elektroskop zum Ausschlag, welcher, wenn man das vergrößerte Bild des beleuchteten Elektroskops mittels einer Linse auf einem Schirme entwirft, weithin wahrgenommen werden kann.

Eine neue Methode, e. S. in Drähten zu beobachten und die sich bildenden stehenden Wellen zu messen,

Fig. 1.

Fig. 2.

Elektrische Schwingungen in Drähten.

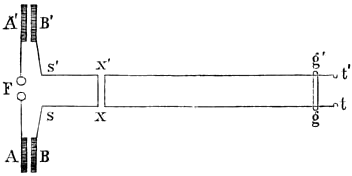
wurde von Lecher (1890) angewendet, A und A′ (Fig. 1) sind quadratische Blechplatten von ca. 40 cm Kantenlänge; sie sind mittels eines 100 cm langen Drahtstückes verbunden, das in der Mitte durchschnitten ist und daselbst bei F zwei Messingkugeln trägt. Dieselben stehen durch dünne Drähte mit den Polen eines Funkeninduktors in Verbindung. Den Platten A und A′ gegenüber stehen in einer Entfernung von etwa 4 cm zwei gleichgroße Platten B und B′. Von diesen führen zwei Drähte zuerst nach s und s′ und von da parallel auf eine Länge von 600 cm und mit einem Abstand von ca. 30 cm bis t und t′. Über die Drahtenden t und t′ wird eine Geißlersche Röhre ohne Elektroden gg′ gelegt; dieselbe beginnt infolge der elektrischen Schwingungen in den Drähten zu leuchten. Legt man jetzt, während die Röhre hell leuchtet, einen Drahtbügel xx′ quer über die parallelen Drähte, so verschwindet im allgemeinen das Licht der Röhre augenblicklich. Verschiebt man nun den Querbügel xx′ längs der Drähte, so findet man einige sehr scharf bestimmte Stellen, wo die Röhre plötzlich wieder aufleuchtet. Diese Stellen sind die Schwingungsbäuche der stehenden elektrischen Wellen, welche durch die Interferenz der nach t gehenden und der bei t zurückgeworfenen Wellen in den Drähten entstehen. Die Erscheinung beruht übrigens auf elektrischer Resonanz. Legt man nämlich den Querbügel über xx′, so stellt sich zunächst eine Hauptschwingung her, welche von B über sxx′s′ nach B′ geht. Diese erste Schwingung erzeugt durch Induktion eine zweite Schwingung in xx′, welche sich von t′ über x′x nach t fortpflanzt. Daß die Erscheinung thatsächlich in dieser Weise durch Resonanz zu stande kommt, beweist der folgende Versuch: Man macht den Querbügel aus zwei voneinander isolierten parallelen Drähten, bringt ihn an die Stelle xx′, wo die Röhre hell aufleuchtet, lötet ihn an dieser Stelle fest und spaltet jetzt durch Durchschneiden der Hauptdrähte den Bügel xx′ der ganzen Länge nach entzwei (Fig. 2). Nun ist der erste Stromkreis Bsxx′s′B′ metallisch geschlossen, und daneben, von ersterm vollständig isoliert, liegt der sekundäre Leiter txx′t′. Die Röhre aber leuchtet ganz so wie früher. Durch Aufsuchen der Schwingungsbäuche wurde die Länge der elektrischen Wellen und daraus ihre Fortpflanzungsgeschwindigkeit in Drähten bestimmt. Lecher fand sie bis auf 2 Proz. der Lichtgeschwindigkeit (300,000 km) gleich, während Hertz nur 200,000 km gefunden hatte.

Indem Sarasin und de la Rive (1889 und 1890) die Versuche von Hertz über die Fortpflanzung elektrischer Wellen längs Metalldrähten wiederholten und sich dabei wie dieser zum Nachweis der Bäuche und Knoten kreisförmiger sekundärer Leiter mit einer Unterbrechungsstelle, sogen. Resonatoren, bedienten, fanden sie, daß die ermittelten Wellenlängen sehr wesentlich von den Dimensionen der Resonatoren abhängen, indem jeder andre Resonator auch eine andre Schwingung anzeigt. Sie schlossen daraus, daß das im primären Leiter erregte System elektrischer Schwingungen alle möglichen Wellenlängen zwischen bestimmten Grenzen enthalte, von welchen jeder Resonator diejenige Schwingung gleichsam aussucht und nachweist, deren Periode seiner eignen entspricht. Sie nannten diese Erscheinung multiple Resonanz der elektrischen Schwingungen.

Anmerkungen (Wikisource)

1. Vorlage: Elekrizität