Auszug aus den Anfangs-Gründen aller Mathematischen Wissenschaften/Die Astronomie
Die Astronomie ist eine Wissenschaft von dem grossen Weltgebäude, und den darinnen sich ereignenden Veränderungen.
2. Man theilet die Astronomie in zwey Theile. In dem ersten wird gezeiget, wie das Weltgebäude sich unseren Sinnen vorstellet, wenn wir auf dem Erdboden stehen. In dem anderen Theile untersuchet man die Natur und Eigenschaften der Weltcörper, die wahre Beschaffenheit des Weltbaues, und die wahren Gesetze der Bewegung. Der erste Theil ist bisher Spaerica, der andere aber Theorica genennet worden.
3. Wenn ihr des Nachts den gestirnten Himmel ansehet, so scheinen alle Sterne von euch in gleicher Weite weg zu seyn.
4. Hütet euch aber, daß ihr nicht schliesset, alle Sterne sind gleich weit weg. Denn ihr wisset, daß Sachen neben einander zu stehen scheinen, da die eine euch viel näher ist, als sie andere (§. 55. Optic.).
[374]5. Derowegen siehet die Welt wie eine hohle Kugel aus, in deren Mittelpuncte ihr stehet, und in deren Fläche die Sterne als helle Puncte angeheftet sind (§. 178. Geom.).
6. Weil ihr in dem ersten Theile der Astronomie nur zu wissen verlanget, was für Erscheinungen sich in dem Weltgebäude in Ansehung der Inwohner des Erdbodens ereignen (§. 2.), die Haupt-Erscheinung aber diese ist, daß es euch wie eine Kugel vorkommet (§. 5.); so nehmet an, die Welt sey eine hohle Kugel, in deren Mittelpuncte ihr stehet, und forschet nach, was aus diesem Satze folge; so werdet ihr die Ursache der übrigen Erscheinungen wahrnehmen.
7. Weil ihr in dem Mittelpuncte der Weltkugel stehet; so könnet ihr auch nur auf einmal einen Theil derselben sehen, der andere aber ist vor euren Augen verborgen.
8. Wenn ihr des Nachts auf die Sterne Acht gebet; so werdet ihr wahrnehmen, daß keiner seine Weite von dem andern, hingegen alle zusammen ihren Stand gegen die Erde ändern. Denn die bey eurem Scheitel stunden, sind von ihm in einer Stunde weg, und andere an ihrer Stelle, die vorhin nicht bey ihm waren. Einige sind gar verschwunden, und hingegen an einem andern [375] Orte sehet ihr Sterne, die vorher nicht da waren.
9. Weil ihr immer auf einer Stelle des Erdbodens bleibet; so scheinet es, als wenn die ganze Weltkugel mit allen Sternen sich um die Erde herum bewegete.
10. Da ihr euch nun in dem ersten Theile der Astronomie nur um Erscheinungen bekümmert (§. 2.); so könnet ihr abermals in demselben ohne Verletzung der Wahrheit annehmen, als wenn die Weltkugel sich mit allen Sternen um die Erde herum beweget.
11. Man machet Kugeln aus Kupfer, Messing und Papier, darauf die Sterne in so proportionirter Weite von einander gezeichnet sind, wie sie in dem Himmel erscheinen, nebst einigen Circuln, die man sich auf der Fläche der Weltkugel einbildet, damit man alles dasjenige, was aus der Bewegung der gesamten Sterne erfolget, auf eine leichte Art denen zeigen kan, die entweder nicht nachdenken können, oder nicht wollen. Dergleichen Kugeln nennet man Himmelskugeln (Globos coelestes).

12. Die beiden Puncte P und Q, an welchen sich die Weltkugel um die Erde herum zu bewegen scheinet, nennet man die Weltpole: [376] und zwar insbesondere denjenigen, welcher in dem uns sichtbaren Theile des Himmels ist, P den Nordpol (Polum Arcticum); den ihm entgegengesetzten Q aber, den Süderpol (Polum Antarcticum).[Fig. 1]
13. Die Linie PQ, welche von einem Pole P bis zum andern Q gezogen wird, ist die Welt-Axe (Axis Mundi)..
14. Der Aequator AD ist ein Circul, welcher auf der beweglichen Fläche der Weltkugel in Gedanken beschrieben wird, und von jedem Pole P und Q überall 90 Grade entfernet ist.
15. Der Zenith ist ein Punct Z über eurer Scheitel in der unbeweglichen Fläche der Weltkugel: das Nadir aber der entgegengesetzte Punct N unter den Füssen in eben dieser Fläche.
16. Also hat ein jeder auf dem Erdboden sein besonderes Zenith und Nadir. Und wenn er seine Stelle ändert, so bekommet er ein anderes Zenith und Nadir.
17. Weil die Weltkugel in Ansehung der Erde sehr groß ist: so wird das Zenith nicht merklich verändert, wenn man gleich ein wenig seine Stelle ändert. Dannenhero giebet man einer ganzen, obgleich grossen Stadt nur Ein Zenith.
[377]18. Der MERIDIANVS ist der Circul PZQNP, welcher durch die Weltpole P und Q, und durch das Zenith und Nadir Z und N in der unbeweglichen Fläche der Weltkugel beschrieben wird. [Fig. 1]
19. Gleichwie man einer ganzen Stadt nur Ein Zenith zueignet; so eignet man ihr auch nur Einen Meridianum zu. Bey den Himmelskugeln machet man den Meridianum entweder aus Meßing, oder aus Holz, theilet jeden Quadranten in 90 Grade ein, und hänget innerhalb demselben die Kugel beweglich auf in ihren Polen. Wenn man nun an das Mittel des Meridiam zwischen den Polen einen Stift hält und die Kugel herumwendet: so beschreibet er darauf den Aequatorem (§. 14.). Daher unterscheidet man auch diesen Circul, wenn er beschrieben worden, von den übrigen, die auch darauf stehen, daß er, wenn die Kugel gewendet wird, beständig durch den neunzigsten Grad von dem Pole gehet.
20. Der wahre Horizont HR ist ein Circul in der unbeweglichen Fläche der Weltkugel, welcher von dem Zenith in allen Puncten 90 Grad weg stehet. [Fig. 1]
21. Zu den Himmelskugeln wird der Horizont von Holze etwas breit gemacht und von dem Gestelle getragen. Man kan die Kugeln innerhalb demselben mit dem Meridiano nach Gefallen verschieben, und dadurch den Pol enhöhen und erniedrigen.
22. Der scheinbare Horizont hr ist ein Circul, welcher den Theil der Himmelskugel [378] hZr abschneidet, so auf der Erdfläche in M gesehen werden kan.
23. Die gerade Linie Mr, die aus dem Puncte der Erdfläche M mit dem Diameter des Horizonts HR parallel gezogen wird, heisset die Mittagslinie. [Fig. 1]
24. Wenn ein Stern in dem Horizont erscheinet, da er vorher unter ihm verborgen war, so gehet er auf. Hingegen wenn er in dem Horizont verschwindet, da er vorher über ihn gestanden, gehet er unter.
25. Der Ort, wo die Sterne aufgehen, heisset Morgen, und insbesondere führet diesen Namen der Punct des Horizonts, welcher von dem Meridiano 90 Grad weg ist. Der ihm entgegengesetzte Punct in dem Theile des Horizonts, wo die Sterne untergehen, wird der Abend genennet. Wenn ihr den Morgen zur Rechten und den Abend zur Linken habet; so zeiget die Mittagslinie vor euch den Punct im Meridiano, den man Mitternacht heisset: hinter dem Rücken aber den Punct im Meridiano, den man Mittag nennet. Alle zusammmen bekommen den Namen der vier Hauptgegenden der Welt.
26. Die Tage-Circul (Circuli diurni) sind [379] Circul, welche die Sterne in ihrer Bewegung um die Erde in der unbeweglichen Fläche der Weltkugel beschreiben.
27. Die Mittagslinie zu finden.

1. Beschreibet auf einer Horizontalfläche aus einem Puncte C etliche Circul.[Fig. 2]
2. Richtet in C einen Stift winkelrecht auf, in der Grösse eines halben, oder auch ganzen Schuhes.
3. Vormittags von 9 bis 11 Uhr, und Nachmittags von 1 bis 3 Uhr gebet Acht, in welchen Puncten vor und nach Mittage eines jeden Circuls der Schatten des Stiftes aufhöret, und merket die Puncte H und I, F und G, D und E.
4. Theilet die Bogen DE, FG, HI in zwey gleiche Theile in L, K und B (§. 94. Geom.) und
5. zieht durch den Mittelpunct C und die Puncte L, K und B eine gerade Linie.
Wenn dieses angehet, so habet ihr die verlangte Mittagslinie.
Weil der Stift im Mittelpuncte C stehet; so sind die Schatten von Einer Länge, welche sich in der Peripherie eines Circuls enden (§. 27. Geom.), und dannenhero stehet die Sonne in beiden Fällen gleich hoch, folgends stehet die Sonne gleich weit von dem Meridiano weg. Nun fället der Schatten jederzeit in den Ort der Sonnen gleich über (§. 34. Optic.); darum sind die Punkte D [380] und E; ingleichen F und G, H und I von der Mittagslinie AB gleich weit entfernt. W. Z. E.
28. Es wäre zwar an Einem Circul genug. Allein wenn ihr viel Circul beschreibet, so könnet ihr desto mehr gewiß seyn, daß ihr recht observiret, wenn die Linie durch alle Theilungs-Puncte und den Mittelpunct der Circul gehet. Weil man aber das Ende des Schattens nicht wohl wahrnehmen kan, und doch die Mittagslinie der Grund zu den meisten astronomischen Observationen ist; so pfleget man sie noch auf andere Weise zu finden.
29. Wenn ihr mit einer Perpendicularlinie die Mittagslinie durchschneidet (§. 70. Geom.); so zeiget dieselbe Morgen und Abend (§. 25.).
30. Wenn der Schatten der Mittagslinie decket, und ihr habet an andern Orten Stifte eingeschlagen; so dürfet ihr nur in ihrem Schatten zwey Puncte merken, und ihr könnet durch dieselben auch die Mittagslinie ziehen.
31. So oft der Schatten des Stifts auf die Mittagslinie fället, ist Mittag (§. 34. Optic.).
32. Daher brauchet man die Mittagslinie, die Uhren zu stellen, damit sie mit dem Laufe der Sonne übereinkommen.
33. Wenn der Schatten der Sonne auf die Linie fället, die Abend und Morgen zeiget; so gehet sie recht im Morgen auf.
34. Der Schatten des Stiftes auf der Mittagslinie [381] bleibet nicht beständig von einer Länge, sondern eine Weile nimmet er zu, darnach wieder ab. Derowegen stehet die Sonne nicht alle Tage gleich hoch über den Horizont (§. 39. Optic.); Welches ihr auch an der Sonne selbst mit blossen Augen wahrnehmen könnet.
35. Wenn also die Sonne sich würklich alle Tage um die Erde bewegen sollte; so beschriebe sie nicht wie die andern Sterne ihre Tagecircul mit dem Aequatore parallel, sondern müste sich in Schraubengängen um die Erde bewegen.
36. Eben dergleichen nehmet ihr von dem Monde wahr, als von der Sonne (§. 34.) angemerket worden. Derowegen müste auch dieser sich in Schraubengängen um die Erde bewegen, wenn er würklich alle Tage um die herumgienge.
37. Wenn ihr des Nachts Acht gebet, bey welchen Sternen der Mond stehet, und sehet die folgende Nacht wieder nach; so werdet ihr ihn nicht mehr bey den gestrigen Sternen, sondern bey andern stehen sehen, die in der vorhergehenden Nacht weiter von ihm gegen Morgen stunden, und nach ohngefehr 27 Tagen werdet ihr ihn abermals bey den ersten Sternen antreffen.
38. Demnach scheinet der Mond innerhalb 27 Tagen um den ganzen Himmel herumzulaufen.
[382]39. Daher geschiehet es auch, daß er bald mit der Sonne auf- und untergehet, bald wieder aufgehet, wenn sie untergehet, und untergehet, wenn sie aufgehet.
40. Gebet Acht auf die Sterne, welche in dem Horizont gegen Abend stehen, wenn die Sonne erst untergegangen, und gegen Morgen, kurz vor ihrem Aufgange. Wenn ihr diese Betrachtung des Himmels eine Zeitlang fortsetzet; so werdet ihr wahrnehmen, daß nach einiger Zeit die Sterne nach dem Untergange der Sonne an dem Abendhorizont stehen, die vorher weiter gegen Morgen stunden: hingegen vor der Sonnen Aufgang um den Morgenhorizont Sterne sind, die man vorher nicht sehen konte. Nach Verlauf eines Jahres werdet ihr an dem Abend- und Morgenhorizont wieder die vorigen Sterne antreffen.
41. Also scheinet sich auch die Sonne von Abend gegen Morgen innerhalb einem Jahre um die Erde zu bewegen.
42. Ausser der Sonne und dem Mond werdet ihr auch noch fünf Sterne antreffen, welche nicht immer bey einerley Sternen stehen bleiben, sondern nach einiger Zeit bey Sternen gesehen werden, die vorhin [383] weit von ihnen gegen Morgen stunden. Sie heissen Saturnus, Jupiter, Mars, Venus und Mercurius, und werden mit folgenden Zeichen geschrieben: ♄♃♂♀☿; der Mond und die Sonne aber ☾☉. Saturnus kommet beynahe in 30; Jupiter in 12; Mars in 2 Jahren; Venus und Mercurius mit der Sonne in einem Jahre um den Himmel herum.
43. Die Bewegung, welche von Morgen gegen Abend innerhalb 24 Stunden um die Erde zu geschehen scheinet, nennet man die gemeine Bewegung: die andere aber, welche von Abend gegen Morgen in verschiedener Zeit um den Himmel herum zu geschehen scheinet, heisset die eine Bewegung.
44. Weil die gemeine Bewegung von Morgen gegen Abend, und die eigene von Abend gegen Morgen geschiehet; so können unmöglich beide zugleich wirklich geschehen.
45. Der Weg, welchen die Sonne in ihrer eigenen Bewegung durchzulaufen scheinet, wird die Ecliptick genennet. Da nun die Sonne des Jahres zweymal in den Aequatorem kommet, die übrige Zeit aber entweder über dem Aequatorem in die Höhe, oder wieder unter den Aequatorem niedersteiget, und beynahe eben so lange über ihm, als unter ihm sich aufhält; so bildet man sich [384] die Ecliptick als einen Circul in der unbeweglichen Fläche der Weltkugel ein, welcher den Aequatorem in zwey Puncten durchschneidet, und zwar in zwey halbe Circul theilet.
46. Es wird zwar die Ecliptick wie alle andere Circul in 360 Grade getheilet: doch mit diesem Unterscheide, daß man die Grade nicht in einem fortzählet, wie sonst gewöhnlich. Denn man theilet die Ecliptick in zwölf Theile ein, welche man die zwölf himmlische Zeichen zu nennen pfleget. Und zwar führet jedes Zeichen einen besondern Namen von dem Gestirne, welches vor Zeiten ihm nahe war. Sie heissen nemlich: Widder, Stier, Zwillinge, Krebs, Löwe, Jungfrau, Wage, Scorpion, Schütze, Steinbock, Wassermann, Fische, welche Namen man in folgende Verse gebracht, um sie leichter zu behalten.
- Sunt Aries, Taurus, Gemini, Cancer, Leo, Virgo,
- Libraque, Scorpius, Arcitenens, Caper, Amphora, Pisces.
Man schreibet sie auch auf besondere Art, nemlich


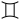

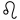
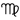


 :[WS 1]
:[WS 1] 

 .
.
Jedes Zeichen hat dreyßig Grade.
47. Die Sterne, welche immer Eine Weite von einander behalten, heissen die Fixsterne: die übrigen aber, welche bald bey diesem, bald bey jenem gesehen werden, die Planeten (§. 42.).
48. Weil man wahrgenommen, daß die Planeten sich nicht in der Ecliptick bewegen, [385] sondern nur zuweilen einmal hineinkommen, gleichwie die Sonne in den Aequatorem, sonst aber bald über die Ecliptick weiter herauf gegen den Nordpol, bald unter die Ecliptick weiter hernieder gegen den Süderpol steigen; so hat man beiderseits in der Weite von 10 Graden zwey Circul mit der Ecliptick parallel gezogen, welche den Raum einschliessen, in welchem die Planeten sich beständig befinden. Diesen Streifen um die Weltkugel nennet man den Thierkreis (Zodiacum) und theilet ihn wie die Ecliptick in 12 himmlische Zeichen.

49. Durch den Anfang des Krebses L und den Anfang des Steinbockes O werden auf der unbeweglichen Fläche der Weltkugel mit dem Aequatore AD zwey Circul LI und KO parallel gezogen, welche man die Tropicos nennet, und zwar LI den Tropicum Cancri, KO den Tropicum Capricorni. [Fig. 1]
50. Es sind also die Tropici Tagecircul, welche die Sonne um die Erde zu beschreiben scheinet, wenn sie in den Krebs und Steinbock tritt (§. 26.).
51. Diese Circul solten von Rechtswegen nicht auf die bewegliche Fläche der Himmelskugel gezeichnet werden. Weil sie aber auf den Erdkugeln nothwendig seyn müssen: so hat man sie auch bloß zu dem Ende auf die Himmelskugel gebracht, damit man sie desto besser gegen die Erdkugel halten kan; welches auch von der Ecliptick zu merken.
[386]52. Die Tagecircul, welche die Pole der Ecliptick um die Weltpole in der unbeweglichen Fläche der Weltkugel beschreiben, heissen die Polarcircul, und zwar der um den Nordpol beschrieben wird, der arctische Polarcircul; der aber um den Süderpol beschrieben wird, der antarctische Polarcircul.
53. Was von den Tropicis erinnert worden (§. 51.), das gilt auch von den Polarcirculn.

54. Ein Verticalcircul ist, welcher durch das Zenith Z und Nadir N um die Weltkugel beschrieben wird. [Fig. 3]
55. Die Höhe eines Sternes ist der Bogen des Verticalcirculs TS, welcher zwischen dem Sterne T und dem Horizint HR enthalten ist. [Fig. 3]
56. Derowegen ist die Mittagshöhe eines Sternes der Bogen des Meridiani MR, der zwischen seinem Mittelpuncte M und dem Horizont HR enthalten ist.
57. Wenn ihr die Sonne recht im Morgen aufgehen sehet (§. 33.), und nach einer guten Uhr die Zeit merket, welche von ihrem Aufgange bis zu ihrem Untergange vorbeystreichet: [387] so werdet ihr inne werden, daß sie völlig 12 Stunden über dem Horizont gewesen. Ihr werdet gleichergestalt befinden, daß die Sterne, welche im Aequatore sind, 12 Stunden über dem Horizont bleiben.
58. Derowegen kommen in Ansehung der Fixsterne und der Sonne der scheinbare Horizont hr und der wahre HR mit einander überein; folgends ist der halbe Diameter der Erde TM, ja der ganze Diameter, und also die ganze Erde in Ansehung der Weite der Sonne und der Fixsterne für einen Punct zu halten. [Fig. 1]
59. Wenn ihr demnach die Sonne und die Fixsterne, folgends auch die Planeten, so nicht niedriger als die Sonne stehen, von der Fläche der Erdkugel ansehet; so ist es eben so viel, als wenn ihr sie aus dem Mittelpuncte T sehen soltet.
60. Die Höhe eines Sternes zu messen.

1. Richtet den Quadranten QCN dergestalt, daß die Linie CN horzontal stehet. [Fig. 4]
2. Verschiebet ihn hin und her, und erhöhet die an seinem Mittelpuncte C befestigte Regel CM so lange, bis ihr durch die an ihr befestigten Dioptern den Stern A erblicket.
Ich sage, der Bogen NM zeiget die Höhe des Sternes.
[388]Wenn der Mittelpunct des Quadrantens C im Mittelpuncte der Erde T stünde; so hätte der Bogen AR so viel Grade als der Bogen NM (§. 28. Geom.). Nun ist es aber in Ansehung der Sonne und Fixsterne gleich viel, ob ihr auf der Fläche der Erde in C, oder in ihrem Mittelpuncte T stehet (§. 59.). Derowegen muß auch in diesem Falle der Bogen AR so viel Grade haben, als der Bogen NM. Der Bogen AR aber ist die Höhe des Sternes (§. 55.). Also wisset ihr, wie viel Grade der Stern über den Horizont erhaben ist. W. Z. E.
61. Wenn ihr die Mittagshöhe eines Sternes verlanget, müsset ihr den Quadranten QCN auf der Mittagslinie perpendicular aufrichten: so stehet er im Meridiano.

62. Die Höhe des Aequatoris AR machet mit der Polhöhe PH 90 Grad. [Fig. 1]
Denn HZR hält 180° (§. 20.) und PA = 90° (§. 14.). Derowegen ist HZR — PA = HP + AR = 90°. W. Z. E.
63. Die Polhöhe an einem Orte zu finden.
1. Wenn des Winters die Nacht länger als 12 Stunden ist, und also der Polarstern zweymal [389] in dem Meridiano gesehen werden kan, nemlich einmal über dem Pole in H, das andere mal unter demselben in K (§. 9. 12.), messet (§. 60.) so wohl die grosse Höhe IH als die kleine IK. [Fig. 4]
2. Ziehet diese von jener ab, und
3. was übrig bleibet, HK, dividiret durch 2; so kommet die Weite des Polarsternes von dem Pole PK heraus.
4. Diese addiret zu der kleinen Höhe des Polarsternes KI.
Die Summe PI ist die verlangte Polhöhe. Z. E. es hat Couplet der jüngere zu Lissabon 1697 gegen das Ende des Decembers observiret
| HI = 41° 5’ 40’’ | |
| KI = 36 28 0 | |
| HK = 4 37 40 | |
| PK = 2 18 50 | |
| KI = 36 28 0 | |
| Polhöhe zu Lissabon. | PI = 38 46 50 |
64. Wenn ihr die Polhöhe von 90° abziehet: bleibet die Höhe des Aequatoris übrig (§. 62.).
| 89° 59’ 60’’ | |
| Polhöhe | PI = 38 46 50 (§. 63.) |
| Höhe des | Aeq. = 51 13 10. |
65. Einen Stern im Meridiano zu oberservieren.
[390]
1. Richtet auf der Mittagslinie BC aus einem Puncte A einen Faden perpendicular auf, und aus D ziehet einen andern Faden DE bis an die Mittagslinie; so ist der Triangel ADE im Meridiano. [Fig. 5]
2. Haltet hinter ihm das Auge, daß der Faden DE den andern AD decket; so ist es gleichfalls im Meridiano.
Derowegen, so bald due Fäden den Stern eurem Auge verdecken, nehmet ihr wahr, daß der Stern in den Meridianum kommet; welches man verlangete.
66. Der Bogen AO des durch die Pole und den Stern beschriebenen Circuls ANHZ, welcher zwischen dem Puncte des Aequatoris A und dem Sterne O enthalten ist, heisset die Declination des Sternes. [Fig. 3]
67. Die Declination eines Sternes zu finden.

1. Messet die Mittagshöhe des Sternes OR oder MR (§. 61.). [Fig. 3]
2. Suchet zwischen ihr und der Höhe des Aequatoris AR (§. 64.) durch die Subtraction der kleineren von der grösseren den Unterscheid AO, oder AM; dieser ist die verlangte Declination.
Z. E. Tycho hat zu Uranienburg die Höhe des Schwantzes im Löwen observiret [391]
| 50° 59’ 0’’ | |
| die Höhe des Aequat. | 34 5 20 |
| Declination des Sternes. | 16 53 40 |
Auf der Himmelskugel führet man den Stern unter dem Meridianum, und zählet daran die Grade unter dem Aequatore bis zu dem Sterne.
68. Wenn ihr die Observationen der alten Astronomorum mit den neuern vergleichet, so werdet ihr finden, daß die Declinationen der Fixsterne veränderlich sind.
69. Wenn euch die Declination eines Sternes bekannt ist, und ihr seine Mittagshöhe observiret (§. 61.); so könnet ihr daraus die Höhe des Aequatoris (§. 67.), und folgends die Polhöhe (§. 62.) finden.
70. Die gröste Declination der Ecliptick zu finden.
1. Wenn die Sonne in den Krebs treten soll, so observiret etliche Tage nach einander ihre Mittagshöhen.
2. Von der grösten ziehet die Höhe des Aequatoris ab; so bleibet (§. 66.) die gröste Declination der Ecliptick, oder der Winkel, den sie mit dem Aequatore machet, und der die Schiefe der Ecliptick genennet wird, übrig.
[392] Z. E. Ricciolus hat A. 1646. die Mittagshöhen der Sonne observiret.
| d. | 20 Jun. | 68° | 59’ | 45’’ | |
| 21 | 69 | 0 | 0 | ||
| 22 | 68 | 59 | 45 | ||
| Also war die gröste Mittagshöhe | 69° | ||||
| 69° | 0’ | 0’’ | |||
| die Höhe des Aequat. | 45 | 31 | 30 | ||
| gröste Declination der Sonne. |
23 | 29 | 30 | ||
71. Die heutigen Astronomi machen sie nur 23° 29’. Insgemein nimmet man sie 23° 30’ an. Derowegen, wenn man von dem Weltpole im Meridiano, darein die Himmelskugel hänget, 23° 30’ gegen den Aequatorem zu zählet; so kan man die Pole der Ecliptick darauf verzeichen. Wenn man nun die Kugel in den gefundenen Polen der Ecliptick einhänget; so lässet sich darauf die Ecliptick eben so wie der Aequator (§. 19.) beschreiben.
72. Eines jeden Puncts der Ecliptick Declination zu finden.
Führet den Grad der Ecliptick auf der Himmelskugel unter den Meridianum; so zeiget sich seine Declination wie bey den Sternen (§. 67.).
73. Wenn ihr die nordische Declination der Sonne von ihrer observirten Mittagshöhe abziehet; so bleibet die Höhe des Aequatoris übrig (§. 67.), und folgends könnet ihr auch die Höhe des Poles (§. 62.) finden. Ihr müsset aber den Ort der Sonne in der Ecliptick wissen. Die südliche Declination wird addiret.
[393]
74. Hingegen wenn euch die Declination der Sonne gegebenen ist, und die Höhe des Aequatoris AR; so könnet ihr die Mittagshöhe der Sonne MR oder OR finden, wenn ihr die nordische Declination zu der Höhe des Aequatoris addiret, oder die südische von ihr subtrahiret. [Fig. 3]
| Z. E. Höhe des Aequatoris Bononien | 45° 30’ 30’’ |
| Declination der |
20 24 57 |
| Mittagshöhe der Sonne | 25 5 33. |
75. Aus der gegebenen Höhe des Aequatoris und der Mittagshöhe der Sonne ihren Ort in der Ecliptick zu finden.
1. Zählet in dem Meridiano von dem Aequatore an gegen Pol zu, gegen welchen die Sonne von ihm abstehet, so viel Grade ab, als ihre Declination gefunden wird.
2. Wendet die Himmelskugel, bis ein Grad der Ecliptick in dem letzten abgezählten Grade zu stehen kommet. Dieser ist der Ort der Sonne.
76. Der Punct des Aequatoris, welcher mit der Sonne oder einem Sterne duch den Meridianum gehet, heisset die gerade Ascension.
77. Die gerade Ascension der Sonne zu finden.
[394]Führet den Grad der Ecliptick auf der Himmelskugel, darinnen die Sonne ist, unter den Meridianum; so stehet der Grad des Aequatoris, den ihr zu wissen begehret, mit darunter.
78. Die schiefe Ascension eines Sternes ist der Punct des Aequatoris, welcher mit einem Sterne durch den Horizont gehet. Hingegen die schiefe Descension ist der Punct des Aequatoris, mit welchem der Stern untergehet.
79. Die Ascensionaldifferenz ist der Unterscheid zwischen den beiden Ascensionen. Die Descensionaldifferenz ist der Unterscheid zwischen der geraden und der schiefen Decension.
80. Aus der gegebenen Polhöhe und dem Orte der Sonne ihre schiefe Ascension zu finden.
Führet den Grad der Ecliptick auf der Himelskugel, in welchem sich die Sonne befindet, in den Morgenhorizont, und darauf in den Abendhorizont; so zeiget sich im ersten Falle die schiefe Ascension, im andern die schiefe Descension, wenn ihr vorher den Pol über den hölzernen Horizont so viel erhöhet, als er über eurem Horizont erhaben ist.
[395]81. Aus dem gegebenen Orte der Sonne in der Ecliptick die Länge des Tages und der Nacht, wie auch den Auf- und Untergang der Sonne zu finden.
1. Erhöhet den Pol der Himmelskugel so viel Grade über den höltzernen Horizont, als er über eurem Horizont erhaben ist.
2. Führet den Grad der Ecliptick, darinnen die Sonne ist, unter den Meridianum, und stellet den Zeiger auf 12. Nachdem also die Kugel auf 12 Uhr zu Mittage gestellet,
3. führet eben diesen Grad in den Morgenhorizont; so zeiget der Stundenzeiger die Zeit, wenn die Sonne aufgehet, und zugleich die halbe Nachtlänge.
4. Führet ihn gleichfalls in den Abendhorizont; so weiset der Stundenzeiger die Zeit, wenn die Sonne untergehet, und zugleich die halbe Tageslänge.

82. Das Azimuth ist der Bogen des Horizonts HS oder SR, welcher zwischen dem Verticularcircul ZS, darinnen die Sonne oder ein anderer Stern sich befindet, und dem Meridiano eines Ortes HZR enthalten. Die Weite aber des Punctes, da die Sonne aufgehet oder untergehet, SO, von dem wahren Morgen oder Abend O, wird AMPLITUDO ORTIVA oder OCCIDUA genennet. [Fig. 3]
[396]83. Daher findet ihr zugleich die Amplitudinem ortivam und occiduam, nebst dem Azimuth mit der schiefen Ascension und Descension (§. 80.).
84. Aus der gegebenen Polhöhe und dem Orte der Sonne ihre Höhe auf jede gegebene Stunde des Tages zu finden.
1. Stellet die Kugel auf 12 Uhr zu Mittage, wie oben (§. 81.).
2. Wendet sie, bis der Zeiger die gegebene Stunde zeiget.
3. Schraubet an das Zenith, das ist, den neunzigsten Grad des Meridiani, von dem Horizont an gerechnet (§. 20.), den Höhen-Quadranten, und wendet ihn, bis er durch den Grad der Ecliptick gehet, darinnen sich Sonne befindet.
4. Zählet die Grade in dem Quadranten zwischen dem Orte der Sonne und dem Horizont.
Wenn man keinen Höhen-Quadranten hat, darf man nur einen Faden dafür nehmen, und den Theil des Fadens zwischen dem Orthe der Sonne und dem Horizont auf dem Aequatore messen.
85. Aus der gegebenen Polhöhe, dem Orte der Sonne und ihrer Höhe, die Stunde des Tages zu finden.
1. Stellet die Kugel auf 12 Uhr zu Mittage (§. 81.).
[397] 2. Befestiget an dem Zenith den Höhen-Quadranten.
3. Wendet sowohl die Kugel als den Quadraten, bis er durch den Ort der Sonne gehet; so weiset der Zeiger die verlangte Zeit.
86. Die Weite zweyer Sterne ist ein Boges eines grösten Circuls der Weltkugel, welcher zwischen ihren beiden Mittelpuncten enthalten.

87. Die Weite zweyer Sterne S und N zu messen. [Fig. 6]
1. Hänget einen Octanten oder Sextanten, dessen Bogen AB der achte oder sechste Theil von einem Circul, dergestalt vertical auf, daß er sich um seinen Mittelpunct C bewegen lässet, und der Bogen ADB gegen den Horizont gekehret ist.
2. Schiebet den Octanten oder Sextanten fort, bis ihr durch die Dioptern an dem Radio BC den Stern S erblicket.
3. Schiebet gleichfalls die bewegliche Regel CD mit ihren Dioptern fort, bis ihr dadurch den Stern N erblicket.
Der Bogen BD ist die verlangte Weite der Sterne S und N.
88. Die gerade Ascension der Fixsterne zu finden.
[398]Führet den Stern unter den Meridianum; so sehet ihr den Grad des Aequatoris, mit dem er darunter kommet, das ist, seine gerade Ascension.

89. Wenn durch die Pole der Ecliptick H und I und den Mittelpunct eines Sternes S ein Circul um die Weltkugel beschrieben wird; so heisset der Bogen von diesem Circul TS, welcher zwischen dem Sterne S und der Ecliptick EL enthalten ist, die Breite des Sternes; hingegen der Bogen der Ecliptick, welcher von dem Anfange des Widders bis zu dem Puncte T gehet, wo der gedachte Circul die Ecliptick durchschneidet, wird die Länge des Sternes genennet. [Fig. 7]
90. Die Länge und Breite eines Sternes zu finden.
Leget den Höhenquadranten an den Pol der Ecliptick dergestalt, daß er durch den Mittelpunct des Sternes gehet; so wird er den Grad der Länge in der Ecliptick abschneiden, und die Breite könnet ihr an dem Quadranten sehen. Hieraus erhellet zugleich, wie man aus der gegebenen Länge und Breite die Sterne auf die Himmelskugel hat zeichnen können.
[399]91. Damit die Sterne in einem Catalogum gebracht, und von den Liebhabern der Sternkunst auch am Himmel unterschieden werden könten; so hat man das ganze himmlische Heer in verschiedene Gestirne vertheilet, und ihnen theils Namen der Thiere, theils gewisser Personen beygeleget. Durch den Thierkreis sind 12 Gestirne zertheilet: der Widder, der Stier, die Zwillinge, der Krebs, der Löwe, die Jungfrau, die Wage, der Scorpion, der Schütze, der Steinbock, der Wassermann, die Fische. Ausser diesen Gestirnen sind in dem nordischen Theile der Weltkugel anzutreffen: der kleine und grosse Bär, der Drache, Cepheus, Bootes, die Nordische Krone, Hercules, die Leyer, der Schwan, Cassiopea, Perseus, Andromeda, der Triangel, der Fuhrmann, Pegasus, das kleine Pferd (Equuleus), der Delphin, der Pfeil, der Adler, der Schlangenmann (Ophiuchus), die Schlange: worzu hernach kommen sind Antinous und das Haar der Barenices. In dem südlichen Theile der Weltkugel sind: der Wallfisch, der Fluß Eridanus, der Haase, Orion, der grosse Hund, der kleine Hund, das Schiff Jasons (Argonavis), die Wasserschlage (Hydra), das Gefässe (Crater), der Rabe. Centaurus, der Wolf, der Altar, die südliche Krone, der südische Fisch, Phoenix, der Kranich, der Indiander, der Pfau, die Indianische Biene, der südliche Triangel, die Fliege, Chamaleon, der fliegende Fisch, Toucan oder die americanische Gans, die Wasserschlange (Hydrus) und Doredo. Von diesen Gestirnen sind die letztern 15 mit dem grösten Theile des Schiffes, des Centauri und des Wolfes, über unserm Horizont, wo die Polhöhe nicht über 51° ist, niemals zu sehen.
92. Es sind einige Sterne, die besondere Namen führen, als Arcturus zwischen den Beinen des Bootis; Gemma der mittlere helle Stern in der Krone; Capella cum boedis an [400] der Schulter des Fuhrmanns; Aldebaran, oder Palilitium, das Auge des Ochsens; Plejades, oder das Siebengestirne auf dem Rücken, und Hyades auf dem Gesichte des Ochsens; Castor und Pollux auf den Köpfen der Zwillinge; Praesepe und Asini auf dem Krebse; Regulus, oder das Herze des Löwens; Spica Virginis in der Hand der Jungfrauen, und Vindemiatrix auf ihrer Schulter; Antares, oder das Herze des Scorpions; Pomahant in dem Maule des südlichen Fisches; Regel in dem Fusse des Orions, und Alcor, das kleine Sternlein über dem mittleren Schwanze des grossen Bärens.
93. Die Poeten der Griechen und Römer haben von dem Ursprunge der Gestirne viele abgeschmackte Mährlein erdichtet, die ihr in des Hygini Poetico Astronomico und Natalis Comitis Mytologia finden könnet.
94. Ausser den Gestirnen der Alten hat man auch einige Unförmige Sterne, aus welchen die neunen Astronomi neune Gestirne zusammengesetzet. Z. E. Hevel setzet zwischen den Löwen und grossen Bären den kleinen Löwen, zwischen den grossen Bären und Fuhrmann über die Zwillinge den Luchs, unter dem Schwantz des grossen Bärens die Jagdhunde Asterion und Chara, in die Hand des Herculis bey Medusens Haupte Cerberum, oder die dreyköpfige Schlange, bey den Pfeiler über dem Adler den Fuchs mit der Gans, zwischen dem Fuß des Pegasi und der Hand der Andromedae die Heydexe (Lacertam), zwischen den Schlangenmann und Antinoum des Sobieskische Schild, Scutum Sobiescianum, unter den Füssen des Löwens Sextantem, den Sextanten. Andere haben vor ihm dazu gesetzt Camelopardalum, Monocerotem, oder das Eichhorn, den kleinen Triangel (Triangulum minus) neben dem grossen, die Carlseiche (Robur Caroli).
[401]95. Unter die Gestirne rechnet man die Milchstrasse, welche um den ganzen Himmel herum durch die Cassiopeam, den Perseum, Fuhrmann, die Füsse der Zwillinge, die Keule des Orions, den Schwanz des grossen Hundes, das Schiff Argus, die Füsse des Centauri, den Altar, den Schwanz des Scorpions, den Fuß des Schlangenmanns, den Bogen des Schützens, und den Schwan gehet, in der Gesalt eines hellen Streifens. Nachdem man den Himmel durch Ferngläser[WS 2] zu betrachten angefangen, hat man gefunden, daß sie von dem Glanze unzähliger kleinen Sternen entstehe, wie vor diesem Democritus (bey dem Plutarcho lib. 3. de placitis Philos. e. 1.). und Ptolemaeos (Almag. lib. 8. c. 2.) wohl gemuthmasset.
96. Nach der scheinbaren Grösse werden die Sterne eingetheilet von der ersten, von der andern, von der dritten, von der vierten, von der fünften und von der sechsten Grösse. Doch kommen nicht alle Sternkundige mit einander darin überein, zu welcher Classe jeder Stern zu rechnen sey. Nach diesen sind die nebelichten Sterne (stellae nebulosae), welche einem hellen Flecken gleichen, durch die Ferngläser aber einen Haufen kleiner Sterne bey einander zeigen. So hat z. E. Galilaeus in dem nebelichten Sterne des Krebses 36 Sterne durch des Fernglas deutlich unterscheiden können.
97. Wenn ihr den Himmel durch Ferngläser betrachten wollet; so werdet ihr viel mehr Sterne als mit blossen Augen sehen. So hat Hugenius durch ein Fernglas von 23 Schuhen anstatt des mittleren Sternes im Schwerdt des Orions 12. (System. Saturn. p. 8.) und Galilaeus im Siebengestirne mehr als 40, in einem kleinen Theile des Orions mehr als 400 Sterne wahrgenommen; wovon ihr ein mehreres in seinem Nuncio sidereo findet. Ja Antonius Maria Schyrlaeus de Rheita (in Oculo Enochi atque Eliae lib. 4. cap. I. memb. 7. f. 197.) hat durch ein holländisches Fernglas in dem Orion allein bis 2000 Sterne gezählet.
[402]98. Hipparchus (wie Ptolemaeus Almag. lib. 7. cap. I. erzählet) muthmassete, daß die Fixsterne ihre Länge ändern, als er mit den Observationen des Arystilli und Tymocharidis die seinen verglich. Ptolemaeus, der beynahe 300 Jahre nach dem Hipparcho lebete, und daher ältere Observationen vor sich hatte, erwiese sie (l. c. cap. 2. & 3.) unwidersprechlich. Er befand aber, daß sie in 100 Jahren einen Grad fortrücketen. Nach diesem hat man die Grösse der Bewegung noch genauer ausgemachet, und kan man füglich für ein Jahr 50’’ zählen, und also für 70 Jahr einen Grad. Die Breite bleibet unveränderlich.
99. Die schiefe Ascension und Descension eines Sternes zu finden.
1. Erhöhet den Pol der Himmelskugel, wie es der gegebene Ort erfordert.
2. Führet den Stern in den Morgen- und Abendhorizont; so sehet ihr seine Ascensionem und Descensionem obliquam (§. 78.).
100. Die Zeit zu finden, welche ein Stern über dem Horizont bleibet.
1. Erhöhet den Pol der Himmelskugel wie vorhin (§. 96.).
2. Führet den Stern in den Morgenhorizont, und richtet den Stundenzeiger auf 12.
[403] 3. Wendet die Kugel, bis der Stern in den Abend-Horizont kommet; so weiset der Stundenzeiger, wie viel Stunden er über dem Horizont bleibet.
101. Aus dem gegebenen Orte der Sonne in der Ecliptick die Zeit zu finden, da ein Stern in den Meridianum kommet, und da er auf- und untergehet.
1. Stellet die Himmelskugel auf 12 Uhr (§. 81.).
2. Führet den Stern unter den Meridianum; so zeiget der Zeiger die Zeit, wenn er darein kommet.
3. Führet ihn gleichergestalt in den Morgen- und Abendhorizont; so weiset der Zeiger die Zeit, wenn er auf- und untergehet.
102. Den Punct der Ecliptick zu finden, mit welchem der Stern in den Meridianum kommet.
Führet den Stern auf der Himmelskugel unter den Meridianum; so sehet ihr den verlagten Grad der Ecliptick.
103. Wenn ihr also wisset, zu welcher Zeit die Sonne in diesen Grad der Ecliptick kommet; so wisset ihr auch, wenn der Stern mit der Sonne durch den Meridianum gehet. Z. E. in dem 1710ten Jahre war die Sonne den 29. Jul. im 7° ![]() [404] anzutreffen. Derowegen ging Sirius diesen Tag um den Mittag durch den Meridianum.
[404] anzutreffen. Derowegen ging Sirius diesen Tag um den Mittag durch den Meridianum.
104. Zu finden, ob der Stern unter einer gegebenen Polhöhe aufgehe, oder nicht.
1. Erhöhet den Pol der Himmelskugel gebührend über den Horizont.
2. Wendet sie herum; so werdet ihr sehen, ob ein Stern auf- oder untergehe, oder ob er immer über oder unter dem Horizont bleibe.
105. Den Punct der Ecliptick zu finden, mit welchem der Stern aufgehet.
Erhöhet den Pol der Himmelskugel gebührend über den Horizont, und führet den Stern in den Horizont; so sehet ihr den Grad der Ecliptick, mit welchem er aufgehet.
106. Wenn ihr den Tag in den Ephemeridibus oder Calendern aufsuchet, an dem die Sonne in denselben Grad der Ecliptick tritt; so wisset ihr, wenn sie mit dem Sterne aufgehet.
107. Suchet ihr aber auf, wenn die Sonne in den entgegengesetzten Grad kommet; so wisset ihr den Tag, an welchem die Sonne untergehet, indem derselbe Stern aufgehet.
[405]108. Eben so könnet ihr den Punct der Ecliptick finden, mit welchem der Stern untergehet; und daher auch den Tag wissen, an welchem er mit der Sonne untergehet; ingleichen den Tag, an welchem er untergehet, indem die Sonne aufgehet.
109. Der Aufgang eines Sternes mit der Sonne, und sein Untergang, indem die Sonne aufgehet, wird ORTVS und OCCASVS COSMICVS genennet. Hingegen der Aufgang und Untergang mit der untergehenden Sonne heisset ORTUS und OCCASUS ACRONYCTUS.
110. Weil es nicht bald finster wird, wenn die Sonne untergehet: so können auch die Sterne nicht bald nach ihrem Untergange gesehen werden. Eben so weil es lichte wird, ehe die Sonne aufgehet, werden die Sterne vor ihrem Aufgange unsichtbar. Derowegen wenn gleich ein Stern etwas eher aufgehet, oder etwas später untergehet als die Sonne, nachdem er vorher mit ihr auf- und untergegangen war; kan er deswegen doch nicht bald gesehen werden, sondern die Sonne muß viel oder wenig nach der scheinbaren Grösse des Sternes unter dem Horizont seyn, ehe der Stern gesehen werden kan. Die Tiefe der Sonne erachtet man aus dem Bogen eines Verticalcirculs, welcher zwischen dem Horizont und der Sonne enthalten ist, und nennet man ihn in diesem Falle ARCUM VISIONIS, oder den Sehungsbogen. Die kleinesten Fixsterne erfordern 18°, die von der sechsten Grösse 17°, die von der fünften 16°, die von der vierten 15°, die von der dritten 14°, die von der andern 13°, die von der ersten 12°, ![]() 11°,
11°, ![]() 11° 30’,
11° 30’, ![]() und
und ![]() 10°,
10°, ![]() 3°. Wenn der Stern aus den Sonnenstrahlen hervorrückt, oder unter dieselbe sich verbirget: nennet man es ORTUM und OCCASUM HELIACUM.
3°. Wenn der Stern aus den Sonnenstrahlen hervorrückt, oder unter dieselbe sich verbirget: nennet man es ORTUM und OCCASUM HELIACUM.
111. Aus dem gegebenen Sehungsbogen und dem Puncte der Ecliptick, mit welchem der Stern aufgehet, den Punct der Ecliptick zu finden, in welchem die Sonne ist, wenn man ihn zuerst im Anfange siehet.
1. Erhöhet gebührend den Pol der Himmelskugel, und führet den Stern in den Morgenhorizont.
2. Befestiget den Höhenquadranten an das Zenith, und suchet dadurch den Grad der Ecliptick, der so viel über den Horizont erhaben, als der Sehungsbogen beträget, als in unserem Exempel 12° (§. 110.); der entgegengesetzte Grad ist der verlangte.
112. Wenn euch der Punct gegeben wird, mit welchem der Stern untergehet; könnet ihr auf gleiche Art finden, in welchem Orte die Sonne ist, indem er sich unter die Sonnenstahlen verbirget.
113. Derowegen wenn ihr den Tag in den Ephemeridibus oder Calendern aufsuchet, an welchem die Sonne in diesen Ort kommet; wisset ihr auch den Tag, an dem der Stern sich unter die Sonnenstrahlen verbirget, oder auch aus denselben zuerst wieder hervorrücket.
[407]114. Der Tagesanbruch (Crepusculum matutinum) wird genennet das Licht, welches vor der Sonnen Aufgang es anfänget helle zu machen. Die Abenddemmerung (Crepusculum vespertinum) ist das Licht, welches nach dem Untergange der Sonne es über unserm Horizont noch helle machet.
115. Weil das Licht durch gerade Linien fortgehet (§. 4. Optic.); so können keine Sonnenstrahlen auf unsern Erdboden von der Sonne fallen, so lange sie unter dem Horizont ist. Doch können sie unsere Luft erreichen, die über der Erde erhaben ist. Derowegen muß die Luft die Sonnenstrahlen auf unsern Erdboden bringen, die sonst vorbey streichen würden, theils indem die von ihr gebrochen (§. 14. Optic.), theils indem sie von den Luftstäubchen zurücke geworfen werden (§. 10. Optic.).
116. Da man erfahren, daß die Sonne höchstens 18 bis 19, nach dem Cassini nur 15° unter dem Horizont seyn muß, wenn die Abenddemmerung aufhören soll, so folget, daß wenn der Unterscheid zwischen der Höhe des Aequatoris und der nordlichen Declination der Sonne nicht über 17° bis 18° ist, der Tag die ganze Nacht durchschimmern muß. Es ist noch eine andere Ursach des Tages und der Abenddemmerung, nemlich der Glanz, der um die Sonne in ihrer Luft erreget wird, gleichwie wir in unserer Luft um jedes Licht [408] einen hellen Glanz antreffen (§. 57. Optic.): dieses aber wird sich erst unten erweisen lassen. Daher scheinet uns der anbrechende Tag wie ein heller Circul vor der Sonne über den Horizont zu fahren.
117. Aus der gegebenen Höhe des Aequatoris zu finden, wie lange an einem Orte der Tag die ganze Nacht durchschimmert.
Ziehet von der Höhe des Aequatoris, oder seiner Tiefe an dem nordlichen Theil des Meridiani 18° ab; so bleibet die geringste Declination der Sonne übrig, welche sie haben kan, wenn der Tag die ganze Nacht durchzuschimmern anfänget und aufhöret.
Z. E. in Halle ist die Höhe des Aequatoris 38° 22’, und also die verlangte Declination der Sonne 20° 22’. Nach dem de la Hire[WS 3] (Tab. Astron. p. 7.) ist die Declination der Sonne 20° 22’ 49’’ wenn die Sonne im 1° ![]() und im 29°
und im 29° ![]() ist. Derowegen muß die Zeit über, das ist, von dem 21 Maji bis den 22 Julii, der Tag daselbst die ganze Nacht durchschimmern.
ist. Derowegen muß die Zeit über, das ist, von dem 21 Maji bis den 22 Julii, der Tag daselbst die ganze Nacht durchschimmern.
118. Aus der gegeben Polhöhe den Anbruch des Tages und das Ende der Abenddemmerung zu finden.
1. Richtet die Himmelskugel auf 12 Uhr (§. 81.).
2. Wendet sie so lange, bis der dem Orte der Sonne [409] entgegengesetzte Grad der Ecliptick 18 Grad über den Abendhorizont erhaben ist; so weiset der Zeiger die Zeit, wenn der Tag anbricht.
3. Wendet die Kugel, bis gedachter Grad über den Morgenhorizont erhöhet ist; so weiset der Zeiger die Zeit, wenn die Abenddemmerung aufhöret.
119. Wenn ihr den Aufgang der Sonne suchet (§. 81.); so giebet der Unterschied zwischen ihm und dem Tagesanbruche die Länge der Morgenröthe. Und auf eine gleiche Art könnet ihr die Länge der Abenddemmerung finden.
120. Aus der gegebenen Polhöhe, der Höhe eines Sternes, und dem Orte der Sonne, die nächtliche Stunde zu finden.
Die Auflösung ist wie oben (§. 85.).

121. Wenn ihr einen Stern S auf der Erdfläche in V ansehet; so sehet ihr ihn in L. Soltet ihr ihn aus dem Mittelpuncte der Erde T sehen; würde er auch in M erscheinen. Der Unterscheid der beiden Oerter, nemlich der Bogen LM, wird PARALLAXIS genennet. [Fig. 8]
122. Der Winkel, den die Linien TS und VS (deren eine aus dem Mittelpuncte der Erde T, die andere von der Erdfläche V in [410] den Mittelpunct des Sternes gezogen wird) mit einander machen, ist der Parallaxi gleich.
Die Parallaxis LM ist der Unterscheid zwischen den Bogen ZM und ZL. Der Bogen ZM ist das Maaß des Winkels MTZ, und weil die Erde in Ansehung der obersten Fläche der Weltkugel, wo ihr euch den Bogen ZH einbilden müsset, ein Punct ist (§. 58.), so ist der Bogen ZL das Maaß des Winkels LVZ (§. 16. Geom.). Demnach ist der Unterscheid dieser Winkel der Parallaxi gleich. Es ist aber TSV der Unterscheid de Winkel MTZ und LVZ (§. 74. Geom.). Derowegen ist der Winkel TSV der Parallaxi gleich. W. Z. E.
123. Wenn ihr demnach die wahre Höhe der Sterne auf eine gegebene Zeit suchet, und sie mit der observirten vergleichet: so könnet ihr ihre Parallaxin finden.
124. Z. E. Philipp Lansberg (Observat. Astronom. Thesaur. fol. 90.) hat An. 1600 d. 1. Mart. nach Mittag um 6 Uhr die Höhe des obern Randes des Mondes in dem Meridiano observiret 64° 7’ 30’’. Den halben Diameter des Mondes befand er 16’ 30’’. Daher war die Höhe des Mittelpuncts im Mond 63° 51’. Die wahre Höhe desselben fand er durch Rechnung 64° 17’ 30’’. Derowegen war die Parallaxis 26’ 30’’. Die Erfahrung hat gelehret, daß die Fixsterne keine merkliche Parallaxin haben, auch der übrigen Planeten Parallaxis so klein sey, daß man sie auf diese Art nicht ausmachen kan.
125. Wenn ein Stern von der Erde weiter weg ist, als ein anderer; so muß seine Parallaxis kleiner seyn, als des anderen.
[411]Es sey der eine Stern in S, der andere in L; so ist des näheren Parallaxis dem Winkel TSV; des weiteren aber dem Winkel TLV (§. 122.) gleich. Nun ist TSV grösser als TLV (§. 74. Geom.). Derowegen ist die Parallaxis des näheren grösser, als die Parallaxis des weiteren. W. Z. E. [Fig. 8]
126. Da nun die Parallaxis immer abnimmet, je weiter der Körper von der Erde weggehet; so muß sie auch endlich unmerklich werden, und ehe dieses geschiehet, so klein, daß man sie auf die (§. 123.) vorgeschriebene Art nicht mehr finden kan, nemlich von wenigen Secunden.
127. Wenn ein Stern im Horizont gesehen wird, so hat er die gröste Parallaxin, die er haben kan.
Verlängert LV in R, und lasset aus dem Mittelpuncte der Erde T die Perpendicularlinie TR herunterfallen. So verhält sich wie der Sinus Totus zu TK, so der Sinus des Winkels K zu TV, und wie der Sinus Totus zu TL, so der Sinus des Winkels L zu TR (§. 19. Trig.). Da nun TK = TL; so ist auch der Sinus des Winkels K zu dem Sinu des Winkels L wie TV zu TR. Und weil TV grösser als TR (§. 144. Geom.); so muß der Winkel K grösser als der Winkel L, folgends die Horizontalparallaxis die gröste seyn (§. 122.). W. Z. E. [Fig. 8]
[412]128. Der Schwanz des Löwens und die Aehre der Jungfrauen sind stets von einander 35° 2’, wenn man sie nahe bey dem Meridiano zu messen pfleget. Allein wenn der erste nur 34° über dem Horizont erhoben ist, stehet die andere beynahe in eben dem Verticalcircul schon in dem Horizont, da sie doch beynahe Grad unter demselben ist. So haben die Holländer, als sie den Winter über hinter der Tartary verblieben, nach einer Nacht von drey Monaten zu Mittage die Sonne gesehen, da sie doch etliche Grade unter dem Horizont war. Keplerus Epit. Astron. lib. I. part. 3. p. 60. 61.
129. Weil die Strahlen der Sterne und der Sonne in unsere Augen fallen, wenn sie noch unter dem Horizint sind, und doch nach geraden Linien fortgehen (§. 6. Optic.); so müssen sie in der Luft gebrochen werden (§. 14. Optic.), und zwar merklich, da sie nicht allein das Bild des Sternes, sondern der ganzen Sonne über dem Horizont erheben können.
130. Da nun wegen der Refraction die Sonne höher gesehen wird, als sie würklich stehet; müsset ihr von den durch den Quadranten gemessenen Höhen der Sonne und Sterne die gehörige Refraction erst abziehen, wenn ihr die wahre Höhe haben wollet.
[413]131. Wie hoch ein Stern in einer observirten Höhe durch die Refraction erhoben worden, auszumachen.
1. Weil die Fixsterne keine merkliche Parallaxin haben (§. 124.); so erwählet euch einen Stern, der im Meridiano dem Zenith sehr nahe kommet, und merket die Zeit, wenn dieses geschiehet, nach einer accuraten Perpendiculuhr, die bey Tage nach der Mittagslinie gestellet worden.
2. Suchet die Höhe des Sternes, und
3. ziehet diese von der observirten Höhe ab. Das übrige zeiget an, wie viel der Stern durch die Refraction gehoben worden.
132. Wenn ihr auf alle Grade die Höhe des Sternes die Grösse der Refraction solchergestalt suchet: so werdet ihr die Tabulam Refractionis bekommen, daraus ihr die observirten Sonnen- und Sternenhöhen corrigiren könnet.
der Astronomie.
So bald die Sonne aufgehet, wird es auf unserm Erdboden lichte, und die Körper, welche ihr entgegengesetzet sind, bekommen einen hellen Glanz. Und so ihr in die Sonne sehen wollet, werden eure Augen geblendet. So bald sich die Wolken vor die Sonne ziehen; verlieren die Körper ihren Glanz, und die Sonne selbst siehet durch die dünnen Wolken unterweilen nur wie ein silberner Teller aus. Wenn die Sonne untergehet, verlieret sich auch der Glanz an den Körpern, und das Licht verschwindet nach und nach gar.
134. Die Sonne ist also die Quelle des Lichtes, welches wir den Tag über auf dem Erdboden geniessen; und daher unserer Erde ein grosses Licht, weil sie es nemlich sehr helle machet.
[415]135. Die Sonne ist ein würkliches Feuer.
Sie leuchtet sehr helle (§. 134.), ihre Strahlen machen warm, ja zünden an und schmelzen die härtesten Sachen, wenn sie entweder durch die Reflexion (§. 24. 25. Catoptr.), oder durch die Refraction (§. 11. Dioptr.) in einem engen Raume zusammengebracht werden. Da nun dieses eben die Würkungen sind, daraus man das Feuer erkennet; so hat man nicht zu zweifeln, daß auch die Sonne ein würkliches Feuer sey. W. Z. E.
136. Als A. 1611. Johann Fabricius zu Anfange des Jahres, und bald darauf im May Christoph Scheiner, ein Jesuit zu Ingolstadt, durch ein Fernglas die Sonne beschaueten; nahmen sie zuerst einige Flecken in der Sonne wahr: welche nach ihnen auch Galilaeus und viele andere Astronomi wahrgenommen, und noch heute zu Tage alle Jahre observiren. Es sehen aber diese Flecken schwarz aus: ihre Figur ist irregulär und veränderlich, wie auch ihre Grösse und Dauer. Scheiner setzet die gröste, welche er im Jenner 1612. observiret, der Veneri gleich. Ricciolus (Almag. Nov. lib. 3. c. 8. f. 96.) hat niemals einen grösseren als den zehenten Theil des Diameters der Sonne gesehen. Sie haben 1. 2. 3. 10. 15. 20. 30. und einige wenige 40 Tage gedauret. Sie bewegen sich an der Sonne, und im [416] Rande verschwindtn sie, nach 13 Tagen kommen sie unterweilen auf der andern Seite wieder hervor. Ihre Bewegung ist im Diameter am stärksten; je weiter sie von demselben weg sind, je schwächer. Auch werden sie an dem Rande schmäler, und viele öfters in eins zusammengezogen, da sie mitten in der Sonne viel breiter und von einander abgesondert erscheinen. Hevelius (Cometogr. lib. 7. f. 424.) erzehlet von zwey Flecken, daß sie im Anfang sehr klein und dünne gewesen, innerhalb zwey Tagen aber zehenmal so groß, und dabey viel dichter und dunkler als vorhin worden. Die meisten Flecken sind mitten dichte, um den Kern herum dünner, und endlich gleichsam mit einem Nebel umgeben. Hevel (l. c. f. 408. seqq.) merket an, daß der Kern wächset und abnimmet, auch meist beständig mitten im Flecken bleibe, und wenn der Flecken bald verschwinden will, in viel Stücke zergehe: gleichwie auch unterweilen in einem Flecken viele Kerne gesehen werden, die öfters in einen zusammen gehen. Kircher hat A. 1684. von dem 6ten April an bis zu dem 17. Jun. einen Flecken in der Sonne gesehen, den auch zu gleicher Zeit Cassini zu Paris observiret. Ja die Flecken, welche der P. Jartoux zu Peckin in China A. 1701. von dem 1. bis zu dem 12. Nov. an der Sonne angetroffen, hat der jüngere Cassini zu Montpellier von [417] dem 31. Oct. bis zu dem 11. Nov. darinnen gesehen. Vid. Acta Erudit. A. 1705. p. 483. & Memories de l’Acad. Royale des Sciences 1701. p. m. 345. Hevel, welcher in seinem Mercurio in Sole viso f. 106. wahrgenommen, daß Mercurius, als er in der Sonne erschien, 27’’ niedriger stund, da die Sonne untergehen wolte, als wie sie hoch über dem Horizont war, hat dergleicher bey den Sonnenflecken nicht verspüret.
137. Weil Mercurius durch die Parallaxin in dem Horizont gesehen worden (§. 136.); so haben die Sonnenflecken in Ansehung der Weite der Sonne von der Erde keine Parallaxin, müssen also derselben sehr nahe, und von unserer Erde weit weg seyn (§. 125.).
138. Und da sie nicht allein ihre Figur und Grösse verändern, sondern auch bald dichter, bald dünner werden, ja mitten in der Sonne entstehen und verschwinden; so ist zu schließen, daß sie aus den Ausdünstungen der Sonne entstehen, und so zu reden, Sonnenwolken sind.
139. Da nun die Ausdünstungen der Sonne über sie steigen, und in einer gewissen Höhe über ihr stehen bleiben; so muß um die Sonne, wie um unsere Erde, Luft seyn, die unten dicker, oben aber dünner, folgends schwerer ist, und eine ausdehnende Kraft hat (§. 20. Aërom.).
[418]140. Wiederum weil nicht allein Ausdünstungen aus dem Sonnenkörper aufsteigen, sondern auch in dem Flecken wieder zerfahren und vergehen, und in die Sonne zurücke herabfallen; so muß nicht allein Materie von verschiedener Art in der Sonne seyn, sondern es müssen auch allerhand Veränderungen in ihr vorgehen.
141. Und weil die Bewegung nicht allein sehr regulär, sondern auch durch den Diameter geschwinder, als durch eine Sehne gehet; so erkennet man, daß die Sonne sich mit ihrer Luft von Morgen gegen Abend innerhalb 27 Tagen und 9 bis 10 Stunden um ihre Axe herum beweget.
142. Da nun aber ihre Figur einmal wie das andere aussiehet, und zwar beständig wie ein Circul; so muß sie beynahe kugelrund seyn.
143. Es reden auch viele von Fackeln in der Sonne, das ist, einigen Theilchen derselben, die viel heller als die andern leuchten. Hevel will (Selenogr. prolegom. f. 87.) den 20. Jul. 1634. einige observiret haben, die den dritten Theil des Diameters der Sonne eingenommen. Auch will er wahrgenommen haben, daß die Flecken sich öfters in Fackeln, selten aber die Fackeln in Flecken verwandelt. Vid. Appendix ad Selenograph. [419] f. 505. 509. Hugenius erinnert in seinem Cosmoth. lib. 2. p. m. 107. daß er niemals dergleichen finden können, sondern nur in der wölkichten oder nebelichten Materie um die Flecken, dergleichen auch bisweilen sich allein sehen lässet, einige Theile heller als die Flecken erblicket. Auch schreibet er die kleine Ungleichheit, welche zuweilen an dem Rande der Sonne sich zeiget, der Bewegung der Dünste in unserer Luft zu.
144. Ich halte demnach das Bildniß der Sonne für erdichtet, welches Scheiner und Kircher abgemahlet, und Zahn nebst anderen aus ihnen genommen.
145. Die Sonnenflecken zu observiren.
Nehemet zwey gefärbte Gläser, und leget sie auf einander, darzwischen aber ein weisses Papier, darein ihr mit einer Nadel ein Löchlein gestochen; so könnet ihr ohne Verletzung des Gesichtes in die Sonne sehen, und die Flecken, so einige vorhanden, entdecken.
Lasset das Augenglas in einem Fernglase über dem Lichte schwarz anlaufen, oder auch ein Fernglas aus Glase von verschiedener Farbe machen, als aus grünem, rothen, blauen, gelben; so könnet ihr abermal unverletzet in die Sonne sehen.
[420]Lasset durch ein Fernglas in ein verfinstertes Zimmer das Bild der Sonne auf eine mit weissem Papier überzogene Tafel fallen; so werden sich darauf die Flecken zugleich mit abmahlen, und ihr könnet ihren rechten Ort, ihre Figur und Grösse ohne Mühe bekommen. Weil aber das Bild der Sonne sich verkehret darstellet; so dürfet ihr nur die Peripherie der Flecken mit einer subtilen Nadel durchstechen, und sie erscheinen auf der andern Seite des Papieres recht.
146. Unterweilen verlieret die Sonne bey hellem Himmel ihren Schein nach und nach, meistens nur in einem Theile. Es lässt aber nicht anders, als wenn eine schwarze Scheibe von Abend gegen Morgen in die Sonne hinein rückete. Und zwar geschiehet solches zu der Zeit, wenn die Sonne und der Mond in Einem Orte des Himmels gesehen werden, oder im Neumond. Absonderlich ist merkwürdig, daß der verfinsterte Theil der Sonne nicht an allen Orten gleich groß. Auch ist wohl zu behalten, daß denen, die weiter gegen Abend liegen, die Sonne eher scheinet ihr Licht zu verlieren, als denen gegen Morgen: hingegen auch in dem ersten Orte ihr Licht geschwinder wieder bekommet, als in dem andern.
147. Weil die Sonne nicht an allen Orten [421] des Erdbodens zu gleicher Zeit, auch nicht gleich viel von ihrem Lichte verlieret; so kan es keine würkliche Beraubung des Lichtes seyn, sondern es muß nur ein dichter und schattichter Körper zwischen unser Auge und die Sonne treten, welcher die Sonnenstrahlen nicht durchlässet, und so weit als die Sonne von uns zu seyn scheint, ob er gleich in der That von ihr weit weg seyn kan (§. 55. Opic.).
148. Dieser Körper muß rund seyn, weil er sich als eine Scheibe auf der Sonne darstellet.
149. Da nun der Mond sich von Abend gegen Morgen beweget (§. 37.), und zu der Zeit, da die Sonne ihr Licht verlieret, zwischen die Erde und die Sonne kommet (§. 146.), er auch, wenn er voll ist, wie eine runde Scheibe aussiehet; so ist kein Zweifel, daß nicht der Mond derjenige Körper sey, welcher uns auf eine Zeit des Sonnenlichtes beraubet. Und muß daher der Mond das Licht der Sonne nicht duchfallen lassen, und also ein dichter schattichter Körper seyn.
150. Die Sonnenfinsterniß ist eine Bedeckung der Sonne von dem Mond, welcher zwischen der Erde und der Sonne stehet.
151. Als die Sonne A. 1706. verfinstert [422] ward, sahe man einen Ring um den Mond, der mit seinem Rande parallel war, nahe an dem Monde dichte aussahe, aber immer dünner wurde, bis er sich in einer völligen Peripherie unvermerkt verlohr. Der Herr von Tschirnhausen in Dreßden hat durch ein sechzehenschuhiges Fernglas wahrgenommen, daß kurz vor dem Anfange der Finsterniß das Sonnenlicht an dem Orte zu zittern angefangen, wo der Mond eingerücket. Eben dergleichen hat er in dem letzten Zolle des Sonnenlichtes angemerket, als er verfinstert war: und ich habe es zu anderer Zeit in dem Rande der Sonne durch ein achtschuhiges Fernglas observiret, da sie aus den Wolken an dem Horizont hervorbrach, und nach langem Regen die Luft voller Dünste war; welches aber verschwand, als die Sonne höher stieg, und die Dünste in der Luft zertheilete. Dergleichen Ring hat man auch in England A. 1711. in einer grossen Sonnenfinsterniß observiret.
152. Wenn der Mond nach dem Untergange der Sonne nahe bey dem Horizont gesehen wird, so ist nur ein kleiner Theil erleuchtet. Je weiter er von der Sonne wegrücket, je ein grösserer Theil wird lichte. Wenner 180 Grad, oder den halben Himmel, von der Sonne weg ist, und ihr in Ansehung unserer Erde gegenüber stehet; so [423] hat der ganze Mond Licht. Gehet er weiter fort, und kommet der Sonne wieder näher; so nimmet das Licht wieder ab, bis er es endlich ganz verlieret, wenn er wieder zu der Sonne kommet. Es ist aber, so lange das Licht zunimmet, der lichte Theil gegen Abend; wenn es abnimmet, gegen Morgen gekehret. Absonderlich ist merkwürdig, daß man auch den finstern Theil des Mondes sehen kan, wenn er noch nicht die Hälfte Licht hat, und siehet er wie ein sehr blasses Wölklein aus.
153. Wenn der Mond zu der Sonne kommet und kein Licht hat, nennen wir ihn den Neumond; wenn die Hälfte gegen Abend Licht hat, das erste Viertel; wenn er ganz hell ist, den Vollmond; endlich wenn die Hälfte gegen Morgen scheinet, das letzte Viertel.
154. Der Mond verlieret zuweilen bey hellem Himmel, wenn er mit vollem Lichte scheinen soll, sein Licht entweder ganz, oder zum Theil. Es lässet aber nicht anders, als wenn eine dunkele Scheibe von Morgen gegen Abend in den Mond einrückete. Und ist merkwürdig, daß an allen Orten ein grosser Theil des Mondes verfinstert wird: auch der Mond zu selbiger Zeit entweder in der Ecliptick, oder sehr nahe bey derselben ist.
[424]155. Wenn der Mond mit vollem Lichte scheinet; so stehet die Erde zwischen ihm und der Sonne (§. 152.). Die Erde wirfet einen Schatten der Sonne gegen über (§. 34. Optic.). Da sie nun in der Ecliptick stehet (§. 45.); so fället ihr Schatten gegen den Grad der Ecliptick, welcher von dem Orte 180° entfernet ist. Derowegen da bey diesem Grade sich der Mond befindet, wenn er sein Licht verlieret; so ist keinesweges zu zweifeln, daß die Ursache der Beraubung des Mondenlichtes daher rühre, weil er in den Schatten der Erde kommt.
156. Weil der Mond in dem Schatten der Erde des Lichtes beraubet wird, damit er die Erde erleuchtet; so kan dieses Licht nicht sein eigen seyn, sondern er muß es anders woher haben, und zwar von der Sonnen, massen der erleuchtete Theil beständig gegen sie gekehret wird (§. 152.).
157. Die Mondfinsterniß ist eine Verdunkelung des Mondes durch den Schatten der Erde, darein er kommt.
158. In einigen Finsternissen ist der Mond bey hellem Himmel, da man die kleinesten Fixsterne gar wohl sehen konnte, ganz verschwunden, so daß man den Ort auch durch die besten Ferngläser nicht finden können, wo er gestanden. Dergleichen hat Kepler [425] An. 1580. und 1583. (Astron. Optic. p. 227.) An. 1601. (l. c. p. 279.) und 1620. (Astron. Copernic. lib. 5. p. 825.) ingleichen Hevel (Selenogr. cap. 6. f. 117.) observiret. Als eben dieses in einer Mondfinsterniß An. 1642. d. 14. Apr. RICCIOLUS mit vielen Jesuiten zu Bononien, ingleichen viele durch ganz Holland wahrnahmen; wurde der Mond doch zu Venedig und Wien gesehen, und zwar sahe er in dem ersten Orte ganz roth aus. (Vid. Ricciolus Almag. Nov. lib. 4. c. 6. Schol. 4. f. 203.) In der Mondfinsterniß, welche sich den 23 Decem. 1703 ereignete, sahe der Mond in der gänzlichen Verfinsterung zu Arles dunkelroth und braun, zu Avignon hingegen hellroth aus, ja so helle, als wenn er durchsichtig wäre, und die Sonne von der andern Seite durchschiene. Zu Marseille sahe er gegen Nordwest röthlich, und gegen Südost ganz dunkel aus, und verschwand völlig bey ganz hellem Himmel.
159. Weil die Farben des Mondes nicht beständig einerley sind in seiner Verfinsterung, ja zu einer Zeit an verschiedenen Orten nicht einerley Farben, und in einigen gar keine gesehen werden; so können sie dem Mond nicht eigenthümlich seyn.
160. Da nun keine Farben seyn können, wo kein Licht ist (§. 46. & seqq. Optic.); so muß der [426] Mond auch in dem Erdschatten noch einiges Licht haben. Und da die Strahlen dieses Lichtes in der Luft gebrochen werden, dadurch sie in unsere Augen fallen (§. 129.); so müssen sie an verschiedenen Orten auf verschiedene Art gebrochen werden, denn sonst könnten sie nicht in verschiedene Farben verwandelt werden. Derowegen entstehen die verschiedenen Farben des Mondes in seiner Verfinsterung von der verschiedenen Beschaffenheit der Luft an verschiedenen Orten.
161. Weil die Strahlen der Sonne in unserer Luft gebrochen werden; so fahren sie auch hin und wieder durch den Erdschatten durch, und zwar um so viel mehr, je stärker die Refraction ist; folgends hat der Mond in dem Erdschatten viel oder wenig Licht, nach der Beschaffenheit der Luft, die von der Sonne erleuchtet wird. Derowegen können die Farben an einem Orte in verschiedenen Zeiten unterschieden seyn, ob gleich die Luft daselbst einerley Beschaffenheit hat.
162. Der Mond siehet sowol den blossen Augen, als durch ein Fernglas, an einem Orte heller, als in dem andern aus. Wenn ihr durch ein Fernglas den zu- und abnehmenden Mond betrachtet; so siehet die Peripherie, darinnen sich das Licht endet, in den hellen Orten höckericht, in den dunkelen aber gleich und eben aus. In den grossen Flecken findet man hin und wieder kleine hellleuchtende [427] Theile. Absonderlich aber sind zwey Dinge merkwürdig: nemlich 1. daß einige Theile in dem Mond erleuchtet werden, die von dem erleuchteten Theile abgesondert sind, und in dem noch finsteren liegen; 2. daß ausser den grossen Flecken, die man mit blossen Augen sehen kan, durch die Ferngläser noch andere kleine entdecket werden, welche von Tage zu Tage, ja von Stunde zu Stunde ihre Grösse, Figur uns Stelle ändern, sich in die Runde herum bewegen, und stets der Sonne entgegengesetzt sind. Dieses alles wird von Hevelio in seiner Selenographia umständlich gewiesen.
163. Alle Theile des Mondes werden von der Sonne auf gleiche Art erleuchtet. Da sie nun aber nicht gleich helle aussehen; können sie nicht auf einerley Art die Sonnenstrahlen zurücke werfen, und sind dannenhero auch selbst von verschiedener Art.
164. Weil die Peripherie, darinnen sich das Licht endet, in den Flecken gleich und eben ist; so müssen die Theile des Mondes, welche weniger Licht als die anderen zurücke werfen, auch selbst gleich und eben seyn.
165. Die Theile, welche eher erleuchtet werden, als andere, die dem erleuchteten Theile des Mondes näher liegen, müssen höher als sie seyn.
[428]166. Die veränderlichen Flecken haben alle Eigenschaften des Schattens (§. 35. 39. 43. 44. 45. Optic.).
167. Hevel (Cometograph. lib. 7. f. 363.) hat zu verschiedenen malen wahrgenommen, daß der Mond und seine Flecken nicht klar und helle, wie zu anderer Zeit, ausgesehen: unerachtet er einerley Weite von der Erde und einerley Höhe über dem Horizont gehabt, und der Himmel allenthalben so helle gewesen, daß er die Sterne von der sechsten und siebenten Grösse sehen können, über dieses sich eben des Fernglases bedienet, damit er sonst den Mond zu observiren gewohnt gewesen.
168. Aus den Umständen der Observation erhellet, daß die Ursache, warum der Mond zu einer Zeit dunkeler ausgesehen als zu einer andern, in etwas zu suchen sey, welches nahe um den Mond gewesen, und gehindert, daß man deutlich durchsehen können.
169. CASSINI (Memoires de l’Acad. Royale des Sciences An. 1706. p. m. 327.) hat öfters observiret, daß, wenn Saturnus, Jupiter und einige Fixsterne von dem Mond bedecket worden, die Figur etwas länglicht worden, indem sie dem Rande des Mondes [429] nahe kommen, sowol auf der erleuchteten als finsteren Seite desselben. Hingegen hat er auch sehr oft ihre Figur unverändert gesehen.
170. Weil die Figur der runden Körper durch die Refraction der Strahlen, die von ihnen in das Auge fallen, in ein Oval verwandelt wird; so muß in dem ersten Falle eine dichte Materie um den Mond gewesen seyn, darinnen die Strahlen der Sterne gebrochen worden: in dem andern Falle aber muß sie sich nicht mehr daselbst anzutreffen gewesen seyn.
171. Wollet ihr zweifeln, ob diese Veränderung der Figur von der Refraction verursachet werden könne; so kleibet einen runden Circul von Papier mit Wachs inwendig an ein Glas, oder an ein anderes Gefässe, und giesset Wasser darein. Durch das Wasser wird euch der Circul wie ein Oval aussehen. Daraus verstehet ihr zugleich, warum die Sonne und der Mond im Horizont wie ein Oval aussehen, wenn die Luft daselbst sehr dunstig ist.
172. Der Mond ist ein dichter und dunkeler Körper, der viele Berge, Thäler und Meere hat.
In den Sonnenfinsternissen tritt der Mond zwischen die Sonne und die Erde (§. 146.), und wird also von ihr auf der von uns weggekehrten Seite beschienen. Wenn er nun durchsichtig wäre, würden die Strahlen der Sonne durchdringen [430] und einen hellen Glanz in dem Mond verursachen. Er siehet aber vielmehr in gänzlichen Verfinsterungen der Sonne ganz schwarz aus (§. 151.). Derowegen muß er ein dichter und dunkeler Körper seyn. Welches das erste war.
An der Mondfläche sind einige Theile über die andern erhaben (§. 165.), und zwar merklich, denn sonst könnten wir sie in der Weite nicht sehen (§. 25. Optic.). Die erhabenen Theile nennen wir Berge, die tiefen Thäler. Derowegen sind in dem Monde Berge und Thäler. Welches das andere war.
Wir finden in dem Monde grosse Plätze, die weniger Licht als die andern zurücke werfen, und dabey gleich und eben sind (§. 146.). Nun haben die flüßigen Körper eine ganz gleiche und ebene Fläche, und werfen weniger Licht zurücke als die Erde, weil sie durchsichtig sind, und einen Theil der Strahlen durchfallen lassen. Derowegen müssen die beständigen Flecken des Mondes eine flüßige Materie, und zwar, weil sie keine Farbe haben, auch sich niemals ändern, Wasser seyn. Demnach giebt es Meere im Monde. Welches das dritte war.
173. Solchergestalt sind die hellen Plätze in dem Meere Insuln.
174. Da man aber auch erhabene Oerter in den Meeren des Mondes und an den Ufern observiret; so sind darinnen grosse Steinklippen und Vorgebürge.
[431]175. Ihr werdet diesen Schlüssen desto sicherer trauen, wenn ihr euch mit Heveln (Selenogr. cap. 6. p. 148.) auf einem hohen Thurme oder Berge umsehen wollet. Denn wo das Land eben ist, wird der Horizont auch gleich und eben; wo jenes aber bergicht und felsicht ist, wird dieser ungleich und zackicht seyn.
176. Ihr könnet nicht zweifeln, daß die veränderlichen Flecken, welche lauter Eigenschaften des Schattens haben (§. 166.), würklicher Schatten der Berge und Felsen sind.
177. Weil die Berge in dem Monde einen Schatten werfen; so siehet man auch daraus, daß er ein vor sich finsterer und undurchsichtiger Körper sey.
178. Derowegen wirfet er auch beständig einen Schatten hinter sich der Sonnen gegen über. (§. 34. Optic.).
179. Wenn also eine Sonnenfinsterniß ist; so kommet die Erde in den Schatten des Mondes (§. 150.), gleichwie der Mond in seiner Verfinsterung in den Schatten der Erde tritt (§. 155.). Demnach ist die sogenannte Sonnenfinsterniß in der That eine Erdfinsterniß.
180. Um den Mond herum ist eine schwere Luft, die eine ausdehnende Kraft hat, und [432] darinnen die Dünste aufsteigen, und durch Regen oder Thau wieder herunter fallen.
Wenn das Sonnenlicht durch eine gänzliche Verfinsterung uns entzogen wird, kan man um den Mond einen breiten hellen Glanz sehen, der mit seiner Peripherie ganz parallel ist (§. 151.). Derowegen muß um den Mond eine flüßige Materie seyn, die sich nach seiner Figur accommodiret, und die Strahlen der Sonne, so hineinfallen, brechen und zurückewerfen kan. Diese Materie muß unten dichter und oben dünner seyn; weil der Glanz an dem Rande des Mondes stärker ist als gegen ihr Ende, ja immer nach und nach abnimmt (§. cit.). Dergleichen flüßige Materie, die unsere Erde umgiebet, ist die Luft (§. 20. Aërometr. & §. 129. Astron.). Derowegen ist auch um den Mond herum Luft. Und da wir befinden, daß unsere Luft unten dicker, oben dünner ist, wegen ihrer Schwere und ausdehnenden Kraft (§. 15. 20. Aërom.); so schliessen wir auch billig, daß die Mondluft schwer sey, und eine ausdehnende Kraft habe. Welches das erste war.
Es ist aber die Mondluft nicht immer gleich durchsichtig (§. 167. 168.), verursachet ein Zittern im Lichte der Sonne (§. 151.) und verwandelt zuweilen die runde Figur der Sterne in eine Oval-Figur (§. 169.). Da nun dieses alles in unserer Luft geschiehet, wenn viele Dünste in ihr anzutreffen (§. 151.); so ist kein Zweifel, daß nicht auch die [433] Mondluft zu der Zeit mit vielen Dünsten angefüllet sey, wenn man dergleichen Dinge in ihr wahrnimmet. Welches das andere war.
Allein da die Luft zu anderer Zeit wiederum reine ist (§. 170.); so müssen die Ausdünstungen aus ihr wieder in den Mond herabgestürzet werden, und also fället entweder ein Thau oder Schnee, oder er regnet. Welches das dritte war.
181. Der Mond ist eben ein solcher Körper wie unsere Erde.
Denn er ist vor sich dunkel und undurchsichtig (§. 172. 177.), hat Berge, Thäler und Meere (§. 172.), Insuln, Steinklippen und Vorgebürge (§. 173. 174.). Er wird von einer schweren Luft umgeben, die eine ausdehnende Kraft hat, und darinnen die Ausdünstungen aufsteigen, und Regen, Schnee und Thau erzeugen (§. 180.). Derowegen ist er ein solcher Körper, wie unsere Erde. W. Z. E.
182. Ein MICROMETRUM, das ist, ein Instrument zu machen, dadurch man die Kleinigkeiten in dem Himmel messen kan.

1. In dem Orte eines Astronomischen Fernglases, wo der Brennpunct des Objectivglases ist, befestiget einen Ring von Meßing AB. [Fig. 10]
2. Durch diesen schraubet zwey Schrauben C und D gleichfalls von Meßing mit sehr engen und [434] gleichen Gängen, die im Mittelpuncte des Fernglases zusammenstossen. So ist das Instrument fertig.
Zählet nach einer accuraten Perpendiculuhr die Secunden und Minuten, welche vorbey fliessen, ehe ein Stern, der im Aequatore ist, in dem unbeweglichen Fernglase von dem Ende der einen Schraube bis zu dem andern kommet, und verwandelt sie durch Hülfe der Regel Detri in Minuten und Secunden des Aequatoris; so wisset ihr, wie viel Gewinde von der Schraube auf eine Minute gehen, und könnet daher ein Täfelein ausrechnen, darinnen einer jeden Zahl der Gewinde ihre zugehörige Secunden zugeeignet werden. Wenn ihr nun z. E. nach dem verfinsterten Monden sehet, und die Schrauben dergestalt richtet, daß sie beiderseits die äussersten Puncte an der Peripherie des Mondes berühren, da das Licht sich endet; so dürfet ihr nur zählen, wie vielmal die Schrauben umgewendet werden müssen, ehe sie im Mittelpuncte zusammenstossen. Diese Zahl zeiget in dem verfertigten Täfelein die Größe der Sehne des verfinsterten Theiles in Minuten und Secunden. Solchergestalt könnet ihr durch dieses Instrument die Kleinigkeiten im Himmel messen, die sich durch Quadranten, Sextanten und Octanten nicht messen lassen. W. Z. E.
183. Durch dieses Instrument könnet ihr die scheinbare Länge der Schatten, den die Berge in [435] dem Monde werfen, und der Meere, ingleichen die Weite der Spitze eines Berges, die erleuchtet wird, von dem erleuchteten Theile des Mondes messen.
184. Hevel (Selenogr. c. 8. f. 266.) hat sie in verschiedenen Bergen in andern nur ja des scheinbaren Diameters des Mondes, und an einigen noch geringer gefunden.
185. Wenn ihr die ![]() durch ein Fernglas beschauet, so werdet ihr meistens nur einen Theil derselben erleuchtet sehen, wie in dem Monde, wenn er nicht voll ist. Und zwar ist der erleuchtete Theil beständig der Sonne zugekehret (Hevelius in Prolegom. Selenogr. f. 68. & seqq.) Auch werdet ihr den
durch ein Fernglas beschauet, so werdet ihr meistens nur einen Theil derselben erleuchtet sehen, wie in dem Monde, wenn er nicht voll ist. Und zwar ist der erleuchtete Theil beständig der Sonne zugekehret (Hevelius in Prolegom. Selenogr. f. 68. & seqq.) Auch werdet ihr den ![]() meistens nur zum Theil erleuchtet sehen, und zwar viel oder wenig, nachdem er gegen der Sonne stehet. (Hevelius l. c. f. 74. 75.). Ja auch im
meistens nur zum Theil erleuchtet sehen, und zwar viel oder wenig, nachdem er gegen der Sonne stehet. (Hevelius l. c. f. 74. 75.). Ja auch im ![]() werdet ihr dergleichen wahrnehmen. (Hevelius l. c. f. 66. 67.)
werdet ihr dergleichen wahrnehmen. (Hevelius l. c. f. 66. 67.)
186. Petrus Gassendus hat A. 1631. d. 7. Nov. zuerst, und nach ihm andere zu verschiedenen malen, den ![]() unter der Sonne gesehen, welcher wie ein schwarzer runder Flecken sich durch den Sonnenteller durch zu bewegen schien. Auf solche Art hat Jeremias HOROCCIUS An. 1639. d. 24. Nov. die
unter der Sonne gesehen, welcher wie ein schwarzer runder Flecken sich durch den Sonnenteller durch zu bewegen schien. Auf solche Art hat Jeremias HOROCCIUS An. 1639. d. 24. Nov. die ![]() in der Sonne gesehen: welche Begebenheit, so lange die Welt stehet, sonst nie observiret
[436] worden, auch nicht eher wiederkommen wird, als 1761. den 25 May.
in der Sonne gesehen: welche Begebenheit, so lange die Welt stehet, sonst nie observiret
[436] worden, auch nicht eher wiederkommen wird, als 1761. den 25 May.
187. Wenn ihr aber ordentlich einige Zeit nach einander die ![]() observiret: werdet ihr mit Heveln (Selenogr. Proleg. f. 68. 69.) befinden, daß, wenn sie bald nach dem Untergange der Sonne gesehen wird, sie mit vollem Lichte scheinet; je weiter sie aber von der Sonne wegrücket, immer mehr und mehr von ihrem Lichte verlieret, bis sie endlich in ihrer grösten Entfernung (welche niemals über 47° ist) nur halb erleuchtet erscheinet. Indem sie nach dieser Zeit sich der Sonne wieder nähert, nimmet ihr Licht noch immer mehr und mehr ab, je näher sie der Sonne kommet. Und so bald sie wieder kurz vor der Sonnen Aufgang gesehen wird, ist sie nur ganz wenig erleuchtet. Doch indem sie von der Sonne weggehet, nimmet ihr Licht immer zu, bis sie in dem grösten Abstande von ihr abermal die Hälfte erleuchtet ist. Wenn sie aber zu der Sonne wieder zurücke kehret, nimmet ihr Licht immer zu, daß sie endlich mit vollem Lichte scheinet, wenn sie sich unter die Strahlen der Morgensonne verbergen will.
observiret: werdet ihr mit Heveln (Selenogr. Proleg. f. 68. 69.) befinden, daß, wenn sie bald nach dem Untergange der Sonne gesehen wird, sie mit vollem Lichte scheinet; je weiter sie aber von der Sonne wegrücket, immer mehr und mehr von ihrem Lichte verlieret, bis sie endlich in ihrer grösten Entfernung (welche niemals über 47° ist) nur halb erleuchtet erscheinet. Indem sie nach dieser Zeit sich der Sonne wieder nähert, nimmet ihr Licht noch immer mehr und mehr ab, je näher sie der Sonne kommet. Und so bald sie wieder kurz vor der Sonnen Aufgang gesehen wird, ist sie nur ganz wenig erleuchtet. Doch indem sie von der Sonne weggehet, nimmet ihr Licht immer zu, bis sie in dem grösten Abstande von ihr abermal die Hälfte erleuchtet ist. Wenn sie aber zu der Sonne wieder zurücke kehret, nimmet ihr Licht immer zu, daß sie endlich mit vollem Lichte scheinet, wenn sie sich unter die Strahlen der Morgensonne verbergen will.
188. Die ![]() beweget sich um die Sonne herum, und muß also bald über, bald unter der Sonne, folgends der Erde bald näher, bald weiter von ihr weg seyn, als die Sonne.
beweget sich um die Sonne herum, und muß also bald über, bald unter der Sonne, folgends der Erde bald näher, bald weiter von ihr weg seyn, als die Sonne.
189. Eben dergleichen hat Hevel (l. c. f. 74. & seqq.) von dem ![]() angemerket, welcher niemals weiter als 28° von der Sonne weggehet.
angemerket, welcher niemals weiter als 28° von der Sonne weggehet.
190. Der ![]() beweget sich um die Sonne, muß aber ihr näher sein als die
beweget sich um die Sonne, muß aber ihr näher sein als die ![]() seyn, weil er niemals so weit von ihr, wie sie, weggehet; er ist aber auch unterweilen von der Erde weiter weg, als die Sonne.
seyn, weil er niemals so weit von ihr, wie sie, weggehet; er ist aber auch unterweilen von der Erde weiter weg, als die Sonne.
191. Die Venus heisset der Morgenstern, (Phosphorus oder Lucifer), wenn sie vor der Sonne hergehet; hingegen der Abendstern (Hesperus), wenn sie ihr nachfolget.
192. De la Hire hat An. 1700 (Memoires de l’Academie Royale des Sciences An. 1700 p. 288. & seqq.) durch ein sechzehnschuhiges Fernglas in der ![]() grössere Berge als im Monde observiret. Sie sahe aber durch sein Fernglas dreymal so groß aus, als der Mond mit blossen Augen gesehen wird. In den übrigen Planeten hat man keine Berge wahrnehmen können.
grössere Berge als im Monde observiret. Sie sahe aber durch sein Fernglas dreymal so groß aus, als der Mond mit blossen Augen gesehen wird. In den übrigen Planeten hat man keine Berge wahrnehmen können.
193. Cassini hat zu verschiedenen malen in der ![]() zwey Flecken observiret. Eben so hat er An. 1666. den 3. Martii zu Bononien im
zwey Flecken observiret. Eben so hat er An. 1666. den 3. Martii zu Bononien im ![]() vier dunkele Flecken durch ein Fernglas
[438] von 16 Schuhen; und den 24. Febr. zwey andere viel grössere gesehen, welche letztere zu eben der Zeit Campani zu Rom duch ein Fernglas von 35 Schuhen entdecket. Er hat auch An. 1665. in dem
vier dunkele Flecken durch ein Fernglas
[438] von 16 Schuhen; und den 24. Febr. zwey andere viel grössere gesehen, welche letztere zu eben der Zeit Campani zu Rom duch ein Fernglas von 35 Schuhen entdecket. Er hat auch An. 1665. in dem ![]() zwey Flecken, An. 1690. zwey andere kleinere, und An. 1691. noch zwey andere weisse wahrgenommen. In dem
zwey Flecken, An. 1690. zwey andere kleinere, und An. 1691. noch zwey andere weisse wahrgenommen. In dem ![]() aber, welcher der Sonne sehr nahe ist, hat man wegen seines hellen Lichtes, und in dem
aber, welcher der Sonne sehr nahe ist, hat man wegen seines hellen Lichtes, und in dem ![]() wegen seiner allzugrossen Weite von der Erde noch keine Flecken entdecken können. In dem
wegen seiner allzugrossen Weite von der Erde noch keine Flecken entdecken können. In dem ![]() sah Hugenius An. 1656. einen breiten dunkelen Streif, der mitten durchging, und beynahe den dritten Theil des Diameters durchgehends breit war. Sonst trifft man beständig in dem Jupiter Steifen an, wiewohl nicht immer auf einerley Art. Denn zuweilen ist nur einer, zuweilen sind drey und mehrere, insgemein zwey: auch werden sie nicht immer an einem Orte gefunden, und verändern ihre Weite gegen einander.
sah Hugenius An. 1656. einen breiten dunkelen Streif, der mitten durchging, und beynahe den dritten Theil des Diameters durchgehends breit war. Sonst trifft man beständig in dem Jupiter Steifen an, wiewohl nicht immer auf einerley Art. Denn zuweilen ist nur einer, zuweilen sind drey und mehrere, insgemein zwey: auch werden sie nicht immer an einem Orte gefunden, und verändern ihre Weite gegen einander.
194. Aus den Observationen der Flecken hat Cassini geschlossen, daß sich ![]() innerhalb 9 Stunden 56 Minuten,
innerhalb 9 Stunden 56 Minuten, ![]() innerhalb 24 Stunden 40 Min. und
innerhalb 24 Stunden 40 Min. und ![]() innerhalb 24 Stunden um ihre Axe bewegen, und daher die Gestalt einer Kugel haben.
innerhalb 24 Stunden um ihre Axe bewegen, und daher die Gestalt einer Kugel haben.
195. Derowegen ist glaublich, daß auch die übrigen beiden Planeten ![]() und
und ![]() sich um ihre
[439] Axe herum bewegen, unerachtet man noch keine Observationen vor sich hat, daraus man dieses gewiß schliessen, und die Zeit, innerhalb welcher solches geschiehet, determiniren könte.
sich um ihre
[439] Axe herum bewegen, unerachtet man noch keine Observationen vor sich hat, daraus man dieses gewiß schliessen, und die Zeit, innerhalb welcher solches geschiehet, determiniren könte.
196. Von dem Monde hat man dafür gehalten, daß er sich nicht um seine Axe beweget, indem er beständig immer Eine Seite der Erde zukehret. Allein Newton hat zuerst dafür gehalten, daß er sich in so langer Zeit um seine Axe einmal herum beweget, als er braucht, um die Erde herum zu kommen. Dann dadurch geschiehet es, daß er der Erde beständig Eine Seite zukehret, ausser daß er zuweilen einen Schwung bekommet, welchen man daraus siehet, daß auf der einen Seite einige Berge und Flecken verschwinden, auf der andern aber andere zum Vorschein kommen. Es wird aber durch diesen Schwung (den die Astronomi motum librationis nennen) gar wenig von der andern Seite des Mondes zu Gesichte gebracht.
197. Simon Marius hat zuerst A. 1609. gegen das Ende des Novembris kleine Sternlein um den Jupiter wahrgenommen, die er Anfangs für Fixsterne gehalten, bis er gemerket, daß sie mit dem Jupiter fortrücketen, und doch zugleich in Ansehung des Jupiters ihre Stelle veränderten. Da er also inne worden, daß es Jupiters Monden wären, hat er von dem 29 Decembris an, seine Observationen aufzuschreiben angefangen; wie er in der Vorrede über seinen Mundum Jovialem, der zu Nürnberg 1614. in 4. herauskommen, erzehlet. Bald darauf, nemlich den 7. Jan hat Galilaeus Galilaei [440] eben dieselben Sterne gesehen und noch im selbigen Jahre in seinem Nuncio sidereo, den er zu Florenz in 4, herausgab, seine Observationen bekannt gemachet.
198. Diese Jupiters-Monden werden auch seine Trabanten (Satellites Jovis) genennet. Galilaeus hieß sie Sidera Medicaea. Man pfleget auch insbesondere mit dem Mario den ersten den Jupiters-Mercurium, den andern die Jupiters-Venerem, den dritten den Jupiters-Jupiter, und den vierten den Jupiters-Saturnum zu nennen.
199. Cassini hat nach vielen mit grossem Fleisse angestellten Observationen endlich gefunden, daß unter den Trabanten des Jupiters der erste in 1 Tage 18 Stunden 28 Minuten und 36 Secunden; der andere in 3 T. 13 St. 18 M. 52 Sec. der dritte in 7 T. 3 St. 59 Min. 40 Sec. und der vierte in 16 T. 18 St. 5 Min. und 6 Sec. um ihn herum gehe.
200. Galilaeus und Marius haben angemerket, daß der erste nicht weiter als 3, der andere höchstens 5, der dritte 8, der vierte 14 Diameter des Jupiters von ihm weggehe, wiewol Marius für den letzten nur 13 setzet.
201. Die Jupiters-Monden werden auf eine Weile unsichtbar, wenn sie dergestalt zu stehen kommen, daß durch den Jupiter [441] und sie aus der Sonne eine gerade Linie gezogen werden kan. Eben dieses hat Maraldi und der jüngere Cassini zuerst A. 1715. von den Saturnus-Monden observiret. Memories de l’Acad. Roy. des Scienc. A. 1715. p. m. 57.
202. Sie werden also ihres Lichtes bey hellem Himmel beraubet, wenn die Sonne sie nicht bestrahlen kan, das ist, verfinstert (§. 157.).
203. Derowegen werden sie von der Sonne erleuchtet, und sind demnach finstere Körper, wie der Mond.
204. Weil Jupiter und Saturnus ihnen kein Licht geben; so müssen sie auf der Seite, die von der Sonne weggekehret ist, auch kein Licht haben.
205. Wenn dem Jupiter seine Monden, entweder unter ihm, oder über ihm, zu nahe kommen, kan man sie für seinen Glanze eine Weile nicht sehen. Wenn sie zwischen der Sonne und dem Jupiter stehen, bemerket man einen kleinen runden Flecken auf ihm. A. 1707. d. 26. Martii hat Maraldi durch ein Fernglas von 34. Schuhen den vierten Mond durch den Jupiter in Gestalt eines dunkelen Fleckens sich bewegen gesehen. So bald er aber durchkommen, hat er ihn an dem Rande des Jupiters auf [442] gewöhnliche Art erblicket. Eben dergleichen Flecken hat er im Jupiter den 4 April durch ein Fernglas von 17 Schuhen observiret, als sich der dritte Mond durch ihn beweget, oder vielmehr vor ihm vorbeygestrichen. Hingegen den 11 April, da eben dieser Mond vor dem Jupiter vorbeystrich, konte er keine Flecken wahrnehmen. (Memoires de l’Academ. Royale des Sciences An. 1707. p. m. 375. & seqq.).
206. Weil die Jupitersmonden finstere Körper sind, und ihr Licht nur von der Sonne bekommen (§. 203.); so müssen sie einen Schatten der Sonne gegenüber werfen (§. 34. Optic.). Derowegen sind die Flecken, welche man an dem Jupiter siehet, wenn sie zwischen ihm und der Sonne stehen, ihre Schatten.
207. Weil nun ihr Schatten Circulrund aussiehet, müssen sie die Gestalt einer Kugel haben (§. 44. 45. Optic.).
208. Wenn sie sich aber selbst auf dem Jupiter als ein dunkeler Flecken darstellen, da sie doch von der Sonne bestrahlet werden; müssen nothwendig Veränderungen in ihrer Luft vorgehen, welche verhindern, daß das Sonnenlicht nicht auf einerley Art reflectiret werden kan. Dergleichen auch geschehen muß, wenn ihr Schatten auf dem Jupiter grösser als sie selbst aussiehet.
[443]209. Durch grosse Ferngläser siehet man 5 kleine Sterne um den ![]() sich herum bewegen. Den ersten hat Cassini durch ein Fernglas von 70. den andern durch ein Fernglas von 35 Schuhen A. 1684 entdecket, nachdem er schon vorher den dritten A. 1672. und den fünften A. 1671. gefunden hatte. (Du Hamel Phil. Vet. & Nov. Tom. 5. Phys. part. 2. tract. 1. diff. 3. c. 9. p. m. 113.) Den vierten hat Hugenius 1655. zuerst gesehen. (Vid. Systema Saturninum p. 3.).
sich herum bewegen. Den ersten hat Cassini durch ein Fernglas von 70. den andern durch ein Fernglas von 35 Schuhen A. 1684 entdecket, nachdem er schon vorher den dritten A. 1672. und den fünften A. 1671. gefunden hatte. (Du Hamel Phil. Vet. & Nov. Tom. 5. Phys. part. 2. tract. 1. diff. 3. c. 9. p. m. 113.) Den vierten hat Hugenius 1655. zuerst gesehen. (Vid. Systema Saturninum p. 3.).
210. Cassini hat aus vielen Observationen erlernet, daß der erste von den Saturnusmonden in 1 Tage, 21 Stunden, 18 Minuten und 31 Secunden, der andere in 2 T. 17 St. 41 M. 27 Sec. der dritte in 4 T. 13 St. 47 M. 16 Sec. der vierte in 15 T. 22 St. 41 M. 11 Sec. und der fünfte in 74 T. 7 St. 53 M. 57 Sec. um den ![]() herumkommen.
herumkommen.

211. Durch die Ferngläser erscheinet ![]() in so seltsamer und veränderlicher Gestalt, daß man eine gute Zeit nicht gewust, was man daraus machen solte. Hugenius hat befunden, 1. daß er unterweilen, wie die übrigen Planeten, rund erscheine, und mitten durch ihn ein dunkeler Strich gehe:[Fig. 13, N 1] 2. daß er unterweilen zwey helle Armen habe, die zu beiden Seiten angesetzet erscheinen, wo vorhin der dunkele Strich durchging, [Fig. 13, N 2] und nach einer
[444] geraden Linie ausgedehnet, an dem Körper aber des Saturni breiter als hinten sind, und spitzig zulaufen, der dunkele Strich hingegen in dem Saturno etwas höher stehe als die Arme; 3. daß die Arme sich spalten, und in zwey Henkel verwandelt werden, der Strich aber unter dem untersten Theile der Henkel in dem Körper des Saturni herunter trete. [Fig. 13, N 3] Vid. Systema Saturninum p. 9. & seqq. Es ist nicht zu vergessen, daß man innerhalb den Henkeln die Fixsterne sehen kan.
in so seltsamer und veränderlicher Gestalt, daß man eine gute Zeit nicht gewust, was man daraus machen solte. Hugenius hat befunden, 1. daß er unterweilen, wie die übrigen Planeten, rund erscheine, und mitten durch ihn ein dunkeler Strich gehe:[Fig. 13, N 1] 2. daß er unterweilen zwey helle Armen habe, die zu beiden Seiten angesetzet erscheinen, wo vorhin der dunkele Strich durchging, [Fig. 13, N 2] und nach einer
[444] geraden Linie ausgedehnet, an dem Körper aber des Saturni breiter als hinten sind, und spitzig zulaufen, der dunkele Strich hingegen in dem Saturno etwas höher stehe als die Arme; 3. daß die Arme sich spalten, und in zwey Henkel verwandelt werden, der Strich aber unter dem untersten Theile der Henkel in dem Körper des Saturni herunter trete. [Fig. 13, N 3] Vid. Systema Saturninum p. 9. & seqq. Es ist nicht zu vergessen, daß man innerhalb den Henkeln die Fixsterne sehen kan.
212. Hieraus hat Hugenius geschlossen, daß um den ![]() sich ein runder und etwas breiter aber dünner Ring bewege, welcher überall von ihm gleich weit abstehet, aber gegen die Ecliptick incliniret ist. Cassini setzet seinen Diameter zu dem Diameter des Planetens wie 11 zu 5.
sich ein runder und etwas breiter aber dünner Ring bewege, welcher überall von ihm gleich weit abstehet, aber gegen die Ecliptick incliniret ist. Cassini setzet seinen Diameter zu dem Diameter des Planetens wie 11 zu 5.
213. Der erste Mond des Saturni ist nach dem Cassini kaum einen Diameter des Ringes von seinem Mittelpuncte weg, der andere 1 , der dritte 1, der vierte 4, der fünfte 10 (du Hamel Physic. Part. 2. Tract. 1. Diss. 3. c. 6. p. m. 113. Tom. 5. Phil. Vet. & Nov.)
214. Saturnus, Jupiter, Mars, Venus und Mercurius sind solche Körper, wie der Mond.
Denn sie sind finster, und haben vor sich kein Licht, als was sie von der Sonne bekommen; welches in der ![]() , dem
, dem ![]() und
und ![]() daraus klar ist, weil beständig nur der Theil erleuchtet, welcher
[445] der Sonne entgegen gekehret ist (§. 185.), auch die ersten beiden Planeten wie ein dunkeler Flecken in der Sonne erscheinen (§. 186.). Von
daraus klar ist, weil beständig nur der Theil erleuchtet, welcher
[445] der Sonne entgegen gekehret ist (§. 185.), auch die ersten beiden Planeten wie ein dunkeler Flecken in der Sonne erscheinen (§. 186.). Von ![]() und
und ![]() ist es schon oben (§. 204.) erwiesen worden, und könnet ihr es daraus abnehmen, weil jener den Schatten seiner Trabanten (§. 206.) auffänget, dieser aber ein sehr schwaches Licht hat. Weil das Sonnenlicht durch den
ist es schon oben (§. 204.) erwiesen worden, und könnet ihr es daraus abnehmen, weil jener den Schatten seiner Trabanten (§. 206.) auffänget, dieser aber ein sehr schwaches Licht hat. Weil das Sonnenlicht durch den ![]() und die
und die ![]() nicht durchfället, wenn sie in der Sonne gesehen werden (§. 186.): so sind sie feste und dichte Körper. Eben dieses erkennet ihr aus dem Schatten von dem Jupiter und Saturnus, dadurch sie ihre Trabanten verfinstern (§. 201. 202.). Durch die veränderlichen Flecken und Streifen in der
nicht durchfället, wenn sie in der Sonne gesehen werden (§. 186.): so sind sie feste und dichte Körper. Eben dieses erkennet ihr aus dem Schatten von dem Jupiter und Saturnus, dadurch sie ihre Trabanten verfinstern (§. 201. 202.). Durch die veränderlichen Flecken und Streifen in der ![]() , dem
, dem ![]() und
und ![]() erkennet man, daß eine Luft um diese Weltkörper sey, die Veränderungen unterworfen, und Dünste aus ihnen in ihr aufsteigen, und bald wieder herunter gestürzet werden, wie aus dem Beweise des dritten Lehrsatzes ganz deutlich abzunehmen (§. 180.). Derowegen können wir auch dieses von den übrigen Planeten annehmen. Eben so, da wir in der
erkennet man, daß eine Luft um diese Weltkörper sey, die Veränderungen unterworfen, und Dünste aus ihnen in ihr aufsteigen, und bald wieder herunter gestürzet werden, wie aus dem Beweise des dritten Lehrsatzes ganz deutlich abzunehmen (§. 180.). Derowegen können wir auch dieses von den übrigen Planeten annehmen. Eben so, da wir in der ![]() grosse Berge antreffen (§. 192.), werden wir nicht irren, wenn wir auch in die übrigen Planeten Berge setzen, unerachtet wir sie durch unsere jetzigen Ferngläser nicht entdecken können, zumal in dem
grosse Berge antreffen (§. 192.), werden wir nicht irren, wenn wir auch in die übrigen Planeten Berge setzen, unerachtet wir sie durch unsere jetzigen Ferngläser nicht entdecken können, zumal in dem ![]() und
und ![]() , die nicht allein von der Erde gar zu weit weg sind, sondern auch stets mit vollem Lichte scheinen.
, die nicht allein von der Erde gar zu weit weg sind, sondern auch stets mit vollem Lichte scheinen.
Da nun sowol die drey oberen, als die beiden unteren Planeten dichte, undurchsichtige [446] und vor sich finstere Körper sind, die ihr Licht einig und allein von der Sonne haben; über dieses grosse Berge in ihnen, und eine veränderliche Luft um sie, auch in der Luft zuweilen starke Dünste, folgends in den Planeten selbst Gewässer angetroffen werden; so sind sie alle zusammen solche Körper wie der Mond (§. 172.). W. Z. E.
215. Weil der Mond eben ein solcher Cörper wie unsere Erde ist (§. 181.); so können wir mit Recht auch die drey oberen und zwey unteren Planeten, nebst des ![]() und
und ![]() Trabanten für Erdkugeln halten.
Trabanten für Erdkugeln halten.
216. Jupiter hat A. 1563. den Saturnum, Mars A. 1591. den 9. Januar. den Jupiter, Venus A. 1590. den 3. Octobr. den Martem, und A. 1599. den 8. Jun. den Mercurium der Erde verdecket. (Kepler in Astron. Optic. p. 305.). Copernicus führet an (Revolut. coelest. l. 5. c. 23.), daß der Mond A. 1529. die ![]() verdecket. Und Ricciolus (Almag. Nov. lib. 7. Sect. 6. c. 14. f. 721.) bringet Exempel von Bedeckung der Fixsterne durch den
verdecket. Und Ricciolus (Almag. Nov. lib. 7. Sect. 6. c. 14. f. 721.) bringet Exempel von Bedeckung der Fixsterne durch den ![]() und
und ![]() bey.
bey.
217. Derowegen muß wenigstens damals, wie die Verdeckungen geschehen, Saturnus weiter als Jupiter, Jupiter weiter als Mars, Mars weiter als Venus, Venus weiter als der Mond, und der verdeckte Fixstern weiter als Jupiter und Mars von der Erde gewesen seyn.
[447]218. Den scheinbaren Diameter der Sterne zu messen.
Dieses geschiehet am füglichsten durch das Micrometrum (§. 182.): nun müsset ihr merken, daß das Augenglas über dem Lichte schwarz anlaufen muß, nicht allein wenn ihr nach der Sonne sehet, sondern auch (wie Hugenius in System Saturnino p. 84. aus eigener Erfahrung erinnert) wiewol viel weniger, wenn ihr den ![]() und die
und die ![]() observiren wollet, damit der allzugrosse Glanz benommen werde, auch die letzteren beide recht rund erscheinen. Imgleichen ist die rechte Bedeckung des Objectivglases in Acht zu nehmen (§. 36. Dioptr.).
observiren wollet, damit der allzugrosse Glanz benommen werde, auch die letzteren beide recht rund erscheinen. Imgleichen ist die rechte Bedeckung des Objectivglases in Acht zu nehmen (§. 36. Dioptr.).
219. Ihr werdet finden, daß der scheinbare Diameter der Sonne, des Mondes und der übrigen Planeten nicht immer von Einer Grösse sey. Derowegen ist klar, daß sie der Erde einmal näher seyn müssen, als das andere (§. 23. Optic.).
220. Hugenius, welcher mit sonderbarer Geschicklichkeit die Grösse des scheinbaren Diameters der Planeten untersuchet, hat folgendes herausgebracht (System. Saturn. p. 77 & seqq.). In der kleinesten Weite von der Erde ist der Diameter des Ringes 1’8”, des Saturni selbst 30”, des Jupiters 1’4”, des Martis 30”, der Veneris 1’25”. In der mittleren Weite setzet er den Diameter der Sonne 30’30”. Von dem Mercurio und dem Monde hat er nichts aufgezeichnet.
221. Wenn ihr durch ein Fernglas auch die grösten Fixsterne [448] betrachtet; so sehen sie nur wie ein Punct aus, und kan ihr Diameter durch das Micrometrum nicht gemessen werden. Hugenius (Cosmoth. lib. 2. p. m. 115.) schätzet ihn nicht viel über vier Tertien in dem Hundsterne.
222. Der scheinbare Diameter des ![]() ,
, ![]() und
und ![]() siehet grösser aus, wenn die von der
siehet grösser aus, wenn die von der ![]() weit weg sind, als wenn sie ihr nahe stehen, so gar, daß der Diameter des
weit weg sind, als wenn sie ihr nahe stehen, so gar, daß der Diameter des ![]() achtmal so groß aussiehet, wenn er von der Sonne 180° wegstehet, als wenn er mit ihr in Einem Orte des Himmels gesehen wird.
achtmal so groß aussiehet, wenn er von der Sonne 180° wegstehet, als wenn er mit ihr in Einem Orte des Himmels gesehen wird.
223. Derowegen sind diese Planeten, sie mögen in dem Himmel stehen, wo sie wollen, der Erde näher, wenn sie der Sonne entgegengesetzet, als wenn sie ihr sehr nahe sind.
224. ![]() kommt beynahe in 10746,
kommt beynahe in 10746, ![]() in 4350,
in 4350, ![]() in 686 Tagen,
in 686 Tagen, ![]() und
und ![]() mit der Sonne um den ganzen Himmel herum. Doch ist die Bewegung einmal nicht so geschwinde, wie das andere, denn sie laufen gleiche Bogen des Thierkreises in ungleicher Zeit durch. Und zwar befindet man die Bewegung einmal am langsamsten, einmal am geschwindesten. Die Oerter, wo dieses geschiehet, sind 180° von einander entfernet.
mit der Sonne um den ganzen Himmel herum. Doch ist die Bewegung einmal nicht so geschwinde, wie das andere, denn sie laufen gleiche Bogen des Thierkreises in ungleicher Zeit durch. Und zwar befindet man die Bewegung einmal am langsamsten, einmal am geschwindesten. Die Oerter, wo dieses geschiehet, sind 180° von einander entfernet.
225. Wenn ![]() ,
, ![]() und
und ![]() der Sonne nahe
[449] sind; so bewegen sie sich geschwinder, als wenn sie von ihr weg sind. Wenn sie 180° von der Sonne wegkommen, gehen sie zurücke, und ehe sie zurücke gehen, ingleichen wenn sie aufhören zurücke zu gehen, stehen sie stille. Sie gehen aber langsamer zurücke als vor sich. Denn da Mars, wenn er zur Sonne kommet, in einem Tage 47 Minuten durchläufet, laufet er in dem Zurückgehen nicht mehr als 24 Minuten durch.
der Sonne nahe
[449] sind; so bewegen sie sich geschwinder, als wenn sie von ihr weg sind. Wenn sie 180° von der Sonne wegkommen, gehen sie zurücke, und ehe sie zurücke gehen, ingleichen wenn sie aufhören zurücke zu gehen, stehen sie stille. Sie gehen aber langsamer zurücke als vor sich. Denn da Mars, wenn er zur Sonne kommet, in einem Tage 47 Minuten durchläufet, laufet er in dem Zurückgehen nicht mehr als 24 Minuten durch.
226. Vergleichet die Zeiten mit einander, in welcher ein Planete geradeläufig, stillestehend und rückgängig ist; so werdet ihr sie auch in Einem Planeten nicht beständig von gleicher Grösse finden. Absonderlich ist in dem ![]() der Unterscheid sehr merklich. Ingleichen ist der Bogen des Thierkreises in diesen Fällen nicht immer von Einer Grösse. Es ist aber ohngefähr
der Unterscheid sehr merklich. Ingleichen ist der Bogen des Thierkreises in diesen Fällen nicht immer von Einer Grösse. Es ist aber ohngefähr ![]() 244,
244, ![]() 284,
284, ![]() 705 Tage rechtläufig; der erste 8, der andere 4, der dritte 2 Tage stillstehend; der erste 136, der andere 119, der dritte 75 Tage rückgängig: und gehet
705 Tage rechtläufig; der erste 8, der andere 4, der dritte 2 Tage stillstehend; der erste 136, der andere 119, der dritte 75 Tage rückgängig: und gehet ![]() beynahe 7,
beynahe 7, ![]() 10,
10, ![]() 10 bis 12 Grade zurücke.
10 bis 12 Grade zurücke.
227. Hingegen ![]() und
und ![]() laufen geschwinde und gerade fort, wenn sie über der Sonne; aber langsam, wenn sie unter der Sonne sind, und werden rückläufig, wenn sie
[450] unter der Sonne sind, und mit ihr in Einem Orte gesehen werden. Es ist aber
laufen geschwinde und gerade fort, wenn sie über der Sonne; aber langsam, wenn sie unter der Sonne sind, und werden rückläufig, wenn sie
[450] unter der Sonne sind, und mit ihr in Einem Orte gesehen werden. Es ist aber ![]() beynahe 542 Tage geradeläufig, einen stehet sie stille, und 42 gehet sie zurücke. Und
beynahe 542 Tage geradeläufig, einen stehet sie stille, und 42 gehet sie zurücke. Und ![]() gehet beynahe 93 Tage gerade fort, einen halben stehet er stille, und 22 läufet er zurücke.
gehet beynahe 93 Tage gerade fort, einen halben stehet er stille, und 22 läufet er zurücke.
228. Die Planeten haben bald eine südische, bald eine nordische, bald gar keine Breite.
229. Derowegen muß ihre Bahn die Ecliptick in zwey Puncten durchschneiden.
230. Der Mond stehet niemals stille, wird auch nicht rückgängig: doch beweget er sich einmal geschwinder, als das andere, und ist der Unterscheid sehr merklich. Wenn der Mond im ersten oder letzten Viertel die gröste Weite von der Erde hat; ist er weiter weg, als wenn er im Neu- oder Vollmond den grössesten Abstand von ihr erlanget. Auch wird die Bewegung viel ungleicher um die Viertel, als im neuen und vollen Lichte gefunden.
231. Wir sollen nun zeigen, wie das Weltgebäude beschaffen seyn müsse, damit alles auf dem Erdboden uns so erscheine, wie es jetzt aus den Observationen vorgestellet worden.
[451]
232. Es ist nicht glaublich, daß, wie Tycho de Brahe[WS 4] vorgiebt, die Erde im Mittelpuncte der Welt ruhe, der Mond, die Sonne und die übrigen Planeten nebst den Fixsternen sich innerhalb 24 Stunden von Morgen gegen Abend bewegen, und zwar dergestalt, daß diejenigen Planeten langsamer um sie herum kommen, welche einen kleinen Weg zu laufen haben, als die, so weit von der Erde weg sind, und durch einen grossen Raum sich bewegen müssen. [Fig. 14]
Denn, wenn ihr diesen Satz als wahr annehmet, könnet ihr keine Ursache geben, warum dergleichen von der Bewegung der Sterne auf dem Erdboden wahrgenommen wird, als vorhin angemerket worden. Ihr könnet nur obenhin zeigen, woher es komme, daß die Planeten in verschiedener Zeit sich von Abend gegen Morgen um den Himmel herum zu bewegen scheinen. Nemlich, weil die Fixsterne geschwinder herumkommen, als die Planeten, und unter diesen diejenigen am langsamsten, die der Erde am nähesten sind; so können weder die Planeten insgesamt mit den Fixsternen, noch die unteren mit den oberen morgen wieder in den Meridianum kommen, wenn sie heute mit ihnen durch denselben gegangen, sondern bleiben etwas zurücke weiter gegen Morgen stehen. Z. E. setzet, es sey heute Neumond, und gehe der Mond mit der Sonne durch den Meridianum. [452] Da die Sonne von der Erde weiter weg ist, als der Mond; kommet sie geschwinder als er um die Erde herum. Derowegen, wenn sie morgen wieder in den Meridianum kommet, kan der Mond noch nicht da seyn, sondern er stehet etwas zurücke gegen Morgen. Und also scheinet es, als wenn er zurücke gegangen wäre. Allein dieses einige kan den Satz nicht wahrscheinlich machen. Wie viel sind nicht Dinge, die ihr durch den gegenwärtigen Satz gar nicht erklären könnet? Wenn die Sonne, der Mond und die übrigen Planeten sich um die Erde bewegeten; so beschrieben sie Schraubengänge um dieselbe (§. 35. 36. 219.), und da ihre Weite von der Erde nicht immer einerley ist (§. 223.), wären die Schraubengänge bald weit, bald enge. Aus gegenwärtigem Satze könnet ihr nicht die geringste Ursache geben, woher es komme, daß die Planeten bald einen weiten, bald einen engen Gang um die Erde nehmen, noch auch sagen, wie sie den weiten eben so geschwinde als den engen durchlaufen können. Die Sonne schweifet niemals über die Tropicos oder Wendecircul, und die Planeten schweifen niemals über den Thierkreis heraus (§. 48. 49.). Ihr könnet aus dem Tychonischen Weltgebäude abermals keine Ursache anzeigen, warum sie ihre Schraubengänge nicht bis gegen die Pole fortführen, und was sie wiederum umkehren heisse. Man hat wahrgenommen, daß der Ort, wo der Planete am weitesten von der Erde weg ist, sich verrücket. Daraus folget, daß, wenn der Planete [453] einmal seine Schraubengänge zu Ende gebracht, und er sie wieder von neuen anfänget, er nicht mehr die alten wiederholet, sondern ganz neue beschreibet. Daher müste er, so lange die Welt stehet, alle Tage einen andern Weg um die Erde genommen haben. Wie ihr dieses aus dem Tychonischen Weltbaue erklären wollet, daran ist nicht einmal zu gedenken. Eben so wenig könnet ihr sagen, warum die Schraubengänge bloß um deßwillen enger werden, als sie sonst seyn würden, weil der Planete auf unserer Erde um einen grösseren Theil des Himmels von der Sonne entfernet zu seyn scheinet (§. 223.). Fraget man ferner, wie es zugehe, daß die Planeten bald stille stehen, bald gar zurücke zu gehen scheinen, das ist, ihre Schraubengänge um die Erde bald in gleicher Zeit mit den Fixsternen, bald geschwinder zu Ende bringen; so weiß man auch hier nicht die geringste Ursache zu geben. Am allerwenigsten kan man zurechte kommen, wenn man die besonderen Umstände dieser Erscheinungen, die oben (§. 225. seqq.) angeführet worden, erkläret wissen will. Also sehet ihr, daß durch den Tychonischen Weltbau nichts begriffen werden kan, was in der Welt vorgehet. Derowegen ist nicht glaublich, daß ihn Tycho recht beschrieben. W. Z. E.
233. Weil man aus dem Tychonischen Weltbaue keine Ursachen der Himmelsbegebenheiten ersehen kan; so ist er auch in der Astronomie zu gar nichts nütze. Denn in dieser Wissenschaft [454] suchen wir die Gesetze der Bewegung der Planeten (§. 2.), damit wir die Himmelsbegebenheiten voraus berechnen können; aus den Tychonischen Schraubengängen aber wird sich niemand in dieser Arbeit zurechte finden, weil man keine Ursache von ihren Veränderungen geben kan.
534. Man will insgemein den Tychonischen Weltbau aus der Schrift behaupten. Z. E. man berufet sich darauf, daß Josua der Sonne befohlen, sie solle stille stehen, und sie sey stille gestanden, Jos. X. 12. 13. Wenn ihr nun fraget, was Josua bey diesen Worten für Gedanken hat haben können; so werdet ihr befinden, er habe verlanget, die Sonne und der Mond solten ihre Stelle in Ansehung der Erde nicht ändern. Daher heisset stille stehen hier so viel, als seinen Stand gegen die Erde nicht ändern, und könnet ihr aus dem Stillstehen der Sonne, welches in der Bibel beschrieben wird, nicht schliessen, daß sie wirklich sich um die Erde bewege. Man führet ferner an, daß gleichwohl die Schrift (Eccles. 1, 5.) mit ausdrücklichen Worten saget: Die Sonne gehet auf und gehet unter, und laufet an ihren Ort, daß sie wieder daselbst aufgehe. Allein weil die Schrift sich nirgends erkläret, was sie durch den Auf- und Untergang der Sonne wolle verstanden haben; so erfordert sie keinen andern Begriff, als den wir insgemein davon haben. Wenn ihr nun auf die auf- und untergehende Sonne Acht habet; so könnet ihr nichts anders wahrnehmen, als daß euch auf eurer Stelle, wo ihr stehet, die Sonne in dem Horizont erscheinet. Und also, wenn die Schrift saget: die Sonne gehet auf und unter; dürfet und könnet ihr euch weiter nichts gedenken, als daß sie in dem Morgen- und Abendhorizont von euch gesehen wird. Eben so, wenn ihr fraget, was ihr euch bey den Worten gedenken sollet: die Sonne läuft an ihren Ort; werdet ihr finden, daß um die Erde laufen nichts anders heisse, als seinen Stand gegen die Erde beständig ändern.

235. Die Sonne lieget beynahe mitten in dem Weltgebäude, und wendet sich daselbst [455] nur um ihre Axe. Um sie bewegen sich ☿, ♀ und die Erde, jener am geschwindesten, diese unter den dreyen am langsamsten, nemlich in einem Jahre. In 24 Stunden aber wendet sich die Erde, wie die übrigen Planeten, um ihre Axe herum. In einer grösseren Weite als sie, beweget sich um die Sonne, und also um sie zugleich, ♂, in noch einer weiteren ♃, und endlich in einer noch weiteren ♄. Die Fixsterne aber sind oben im Firmamente unbeweglich, ausser daß sie sich sonder Zweifel um ihre Axe bewegen. Der ☽ beweget sich um die Erde innerhalb 27 Tagen, aber zugleich mit der Erde in Jahresfrist um die Sonne: gleichwie die Jupiters- und Saturnus-Monden sich um den ♃ und ♄, aber zugleich mit ihnen um die Sonne, bewegen. [Fig. 15]
Wenn ihr euch den Weltbau auf solche Art vorstellet; könnet ihr auf einmal begreifen, woher es komme, daß ihr von der Bewegung der Planeten wahrnehmet, was aus den Observationen angeführet worden. Denn weil die Erde sich innerhalb 24 Stunden um ihre Axe herum beweget; so muß ein Stern nach dem andern um den ganzen Himmel herum in eurem Horizont erscheinen. Und also sehet ihr die Sterne nach einander auf- und untergehen. Und aus eben dieser Ursache gehet die Sonne alle Tage auf und unter, und scheinet sich um die Erde herum zu bewegen.
[456]
Wenn die Erde in 7 ist, sehet ihr die Sonne in ![]() . Kommet sie in 6, so sehet ihr die Sonne in
. Kommet sie in 6, so sehet ihr die Sonne in ![]() . Ist die Erde in 4, so erscheinet die Sonne im
. Ist die Erde in 4, so erscheinet die Sonne im ![]() ; hingegen im
; hingegen im ![]() , wenn jene in 1; in
, wenn jene in 1; in ![]() , wenn sie in 10 ist. Solchergestalt scheinet sich die Sonne innerhalb einem Jahre um die Erde herum zu bewegen. [Fig. 16]
, wenn sie in 10 ist. Solchergestalt scheinet sich die Sonne innerhalb einem Jahre um die Erde herum zu bewegen. [Fig. 16]
Bildet euch ein, es sey die Erde, wo vorhin die Sonne war, und der Mond bewege sich um sie aus 7 in 6, und aus 6 in 5 u. s. w. So sehet ihr ihn auf der Erde anfangs im ![]() , hernach im
, hernach im ![]() , in
, in ![]() u. s. w. Folgends scheinet er auch in 27 Tagen den ganzen Thierkreis durchzulaufen.
u. s. w. Folgends scheinet er auch in 27 Tagen den ganzen Thierkreis durchzulaufen.
Wenn die Erde einen weiteren Weg um die Sonne nimmet, als die ![]() und
und ![]() ; so müssen die beiden Planeten stets entweder vor der Sonne hergehen, oder ihr nachfolgen. Sie können aber nur auf eine gewisse Weite von ihr zu gehen scheinen, und zwar
; so müssen die beiden Planeten stets entweder vor der Sonne hergehen, oder ihr nachfolgen. Sie können aber nur auf eine gewisse Weite von ihr zu gehen scheinen, und zwar ![]() weniger als
weniger als ![]() , dieweil er der Sonne näher als diese ist. Indem aber die Erde sie sowohl als die Sonne umgehet; müssen wir sie gleichfalls in einem Jahre den Thierkreis durchlaufen sehen, unerachtet sie in der Zeit, da sie um die Sonne herumkommen, in der That ihren Lauf um den ganzen Himmel herum vollenden.
, dieweil er der Sonne näher als diese ist. Indem aber die Erde sie sowohl als die Sonne umgehet; müssen wir sie gleichfalls in einem Jahre den Thierkreis durchlaufen sehen, unerachtet sie in der Zeit, da sie um die Sonne herumkommen, in der That ihren Lauf um den ganzen Himmel herum vollenden.
Die Planeten, welche der Sonne näher sind, kommen geschwinder herum, als die weiter von ihr weg sind: denn jene haben nur einen kleinen, diese aber einen viel weiteren Weg zu laufen. Da aber die Planeten sich nicht in Circuln bewegen, in deren Mittelpunct die Erde anzutreffen; so scheinet uns ihre Bewegung einmal geschwinder als
[457]
das andere, und zwar langsamer; wenn sie von der Erde weit weg, als wenn sie ihr nahe sind. Denn setzet z. E. der Planete bewege sich aus Q durch N in S; so wird es euch auf der Erde in T vorkommen, als wäre er den halben Thierkreis LAO durchlaufen, da er doch in der That mehr als die Hälfte seines Weges zurücke geleget. Setzet ferner, er bewege sich aus S durch M in Q; so bildet ihr euch in T ein, er sey den halben Thierkreis OPL durchlaufen, da er doch in der That weniger als die Hälfte seines Weges vollendet. Nun ist NC = CM (§. 27. Geom.) und daher NT grösser als TM. Derowegen scheinet sich der Planete langsamer zu bewegen, wenn er von der Erde weit weg ist, als wenn er ihr nahe ist. [Fig. 17]
Wenn die Erde z. E. in N ist und ![]() in A,
in A, ![]() in B,
in B, ![]() in C; so scheinen euch diese Planeten mit der Sonne an Einem Orte des Himmels zu stehen. Ist aber die Erde in T, und die Planeten sind in den vorigen Oertern; so scheinen sie euch von der Sonne 180° entfernet zu seyn. Eben so verhält sichs, wenn die Erde in N, und die Planeten in D, E, F sind. Darum müssen die oberen Planeten allerdings viel weiter von der Erde weg seyn, wenn sie bey der Sonne sind, als wenn sie weit von ihr weggehen. [Fig. 15]
in C; so scheinen euch diese Planeten mit der Sonne an Einem Orte des Himmels zu stehen. Ist aber die Erde in T, und die Planeten sind in den vorigen Oertern; so scheinen sie euch von der Sonne 180° entfernet zu seyn. Eben so verhält sichs, wenn die Erde in N, und die Planeten in D, E, F sind. Darum müssen die oberen Planeten allerdings viel weiter von der Erde weg seyn, wenn sie bey der Sonne sind, als wenn sie weit von ihr weggehen. [Fig. 15]
Wenn die Erde in N, ![]() in G,
in G, ![]() in H ist; so sind diese beide Planeten ihr näher als die Sonne; ist aber die Erde in T, und die beiden Planeten sind in G und H; so ist die Sonne der Erde näher als sie.
in H ist; so sind diese beide Planeten ihr näher als die Sonne; ist aber die Erde in T, und die beiden Planeten sind in G und H; so ist die Sonne der Erde näher als sie.

Es sey die Erde in A, Jupiter in I, so sehet ihr ihn in a, und mit der Sonne in Einem Orte. Die
[458] Erde komme in B; so rücket ![]() in 2 und ihr sehet ihn in b. Gleichergestalt sehet ihr ihn, wenn er in 3 ist, aus C in c. Darum scheinet er euch in dem Thierkreise gerade fort zu gehen. Hingegen komme die Erde bis in D und der Planete bis in 4; so sehet ihr ihn in d, und aus E, wenn er in 5 ist, in e. Derowegen scheinet er zurückzulaufen, wenn er der Sonne entgegen stehet. Eben so verhält sich die Sache, wenn ihr anstatt des Jupiters den
in 2 und ihr sehet ihn in b. Gleichergestalt sehet ihr ihn, wenn er in 3 ist, aus C in c. Darum scheinet er euch in dem Thierkreise gerade fort zu gehen. Hingegen komme die Erde bis in D und der Planete bis in 4; so sehet ihr ihn in d, und aus E, wenn er in 5 ist, in e. Derowegen scheinet er zurückzulaufen, wenn er der Sonne entgegen stehet. Eben so verhält sich die Sache, wenn ihr anstatt des Jupiters den ![]() und
und ![]() nehmen wollet. [Fig. 18]
nehmen wollet. [Fig. 18]

Allein wenn die Erde in A, ![]() in 1 ist, sehet ihr ihn in a. Kommet sie bis in B und er in 2, so sehet ihr ihn in b, ingleichen aus C, wenn er in 3 ist, in c u. s. w. Darum scheinet er durch den Thierkreis gerade durchzulaufen. Hingegen, kommet die Erde bis D,
in 1 ist, sehet ihr ihn in a. Kommet sie bis in B und er in 2, so sehet ihr ihn in b, ingleichen aus C, wenn er in 3 ist, in c u. s. w. Darum scheinet er durch den Thierkreis gerade durchzulaufen. Hingegen, kommet die Erde bis D, ![]() bis 4; so sehet ihr ihn in d und er scheinet euch rückgängig zu werden, unerachtet er in seinem Wege immer gerade fortgehet. Derowegen wird er rückläufig, wenn er unter der Sonne ist, und mit ihr beynahe an Einem Orte des Thierkreises gesehen wird. Eben so kan man es von der
bis 4; so sehet ihr ihn in d und er scheinet euch rückgängig zu werden, unerachtet er in seinem Wege immer gerade fortgehet. Derowegen wird er rückläufig, wenn er unter der Sonne ist, und mit ihr beynahe an Einem Orte des Thierkreises gesehen wird. Eben so kan man es von der ![]() erweisen. Aus diesem sehet ihr, wie ohne Schwierigkeit die Ursachen von den Himmelsbegebenheiten aus gegenwärtigem Lehrsatze gegeben werden können, und ihr werdet aus dem folgenden ersehen, daß auch die allergenauesten Umstände daraus sich determiniren. Also ist wol nicht zu zweifeln, daß das Weltgebäude in gegenwärtigem Lehrsatze richtig beschrieben sey. W. Z. E. [Fig. 19]
erweisen. Aus diesem sehet ihr, wie ohne Schwierigkeit die Ursachen von den Himmelsbegebenheiten aus gegenwärtigem Lehrsatze gegeben werden können, und ihr werdet aus dem folgenden ersehen, daß auch die allergenauesten Umstände daraus sich determiniren. Also ist wol nicht zu zweifeln, daß das Weltgebäude in gegenwärtigem Lehrsatze richtig beschrieben sey. W. Z. E. [Fig. 19]
236. Weil sich die Polhöhe auf der Erde nicht verändert; so muß die Axe der Erde, indem sie um [459] die Sonne herum gehet, mit der Weltaxe beständig parallel bleiben. Und daher ist eine besondere Bewegung von nöthen, dadurch dieses erhalten wird.
237. Copernicus nennet diese Bewegung motum reflexionis. Damit ihr euch dieselbe desto füglicher einbilden könnet; so setzet, es sey auf eine Flagge eine Kugel dergestalt gemahlet, daß ihre Axe mit der Weltaxe parallel ist. Fahret mit dem Schiffe um eine Insul. Wenn der Südwind bläset; so wird die Flagge beständig gegen Norden stehen, und also die Axe der daran gemahlten Kugel unverändert mit der Weltaxe parallel erhalten werden.
238. Wiederum, indem die Erde sich um ihre Axe beweget, suchet alle Materie, die ihr zugehöret, sich von dem Mittelpuncte des Circuls, in dessen Peripherie sie sich befindet, zu entfernen, und zwar unter dem Aequatore am meisten, gegen die Pole weniger: wie ich in meinen Element Mech. erwiesen. Da nun eben diese Materie vermöge ihrer Schwere gegen den Mittelpunct der Erbe getrieben wird; so muß die vorige Kraft ihr widerstehen (§. 12. Hydrost.). Derowegen muß die Materie leichter über dem Aequatore, als gegen die Pole seyn.
239. Auch dieses hat die Erfahrung bekräftiget. Denn als man die Perpendiculuhren von Paris in die Insul Cayenne in America gebracht, welche nicht über 4 bis 5 Grad von dem Aequatore entfernt ist; hat man befunden, es müsse daselbst das pendulum 1 Linie kürzer als zu Paris [460] seyn, wenn es eine Secunde schlagen soll. Nun ist aber bekannt, daß, wenn im Pendulo die Länge des Fadens unverändert bleibet, die Kugel leichter werden müsse, so es langsamer als vorhin gehet. Hieraus erkennet, wie genau der beschriebene Weltbau mit der Erfahrung übereinstimme.
240. Man nennet den beschriebenen Weltbau den Copernicanischen, weil ihn Copernicus in den neuern Zeiten wieder in Aufnehmen gebracht: denn unter den Alten haben schon Philolaus und andere ihn vertheidiget. Es hat zur Zeit niemand etwas erhebliches wider ihn einwenden können. Was insgemein von Unverständigen angeführet wird, die entweder die Eigenschaft der Schwere vergessen, oder nicht bedenken, daß zugleich die Luft mit der Erde sich innerhalb 24 Stunden um ihre Axe bewege; verdienet nicht beantwortet zu werden. Dergleichen ist, daß ein Stein nicht unten bey dem Thurm fallen könte, wenn er von oben herunter geworfen würde. Der einige Zweifel kan hier entstehen, daß, wenn die Erde einmal in O, das anderemal in M ist, der Fixstern S in Ansehung des Diameters der Erdbahn OM eine merkliche parallaxin haben müste. Dergleichen aber aus den Observationen nicht zu erweisen gewesen. Hierauf hat schon Copernicus geantwortet, es wäre der Diameter der Erdbahn OM in Ansehung der Entfernung des Sternes von der Erde OS oder SM nur für ein Punct zu halten, und daher der Winkel OSM oder die Parallaxis des Fixsternes unmerklich. Man darf nicht einwenden, als wenn solchergestalt der Fixstern beynahe einen so grossen Diameter haben müsse, als die Erdbahn; denn man siehet ihn wegen seines starken Lichtes, und nicht wegen seiner Grösse (§. 298.).
241. Cassini (wie Gregorius in Element. Astronom. Schol. prop. 54. f. 274. anmerket) hat observiret, daß der erste Stern im Widder zuweilen in zwey zertheilet erscheine, dergleichen er auch von dem einen Haupte der Zwillinge gefunden. Einige andere in den Plejadibus und der mittlere in dem Orions-Schwerdte sind ihm zuweilen dreifach, ja vierfach [461] erschienen; dessen Ursache sich gar wohl aus der Bewegung der Erde um die Sonne begreifen lässet. Denn wenn sie in O ist, könnet ihr zwey Sterne, deren einer niedriger ist als der andere, in Einem Orte sehen, die ihr aus M in verschiedene Örter setzet.

242. Die Erde und alle übrigen Hauptplaneten als ![]() ,
, ![]() ,
, ![]() ,
, ![]() und
und ![]() bewegen sich in einer Ellipsi um die Sonne, welche in ihrem einen Brennpuncte S lieget, und zwar dergestalt, daß die Linie SI, welche aus der Sonne in den Mittelpunct des Planetens gezogen wird, in gleicher Zeit gleiche Theile von der Ellipsi beschreibet, so daß der Theil von der Ellipsi ASI sich zu der ganzen Ellipsi verhält, wie die Zeit, da der Planete den Bogen AI durchläufet, zu der Zeit, da er die ganze Peripherie durchwandert. [Fig. 20]
bewegen sich in einer Ellipsi um die Sonne, welche in ihrem einen Brennpuncte S lieget, und zwar dergestalt, daß die Linie SI, welche aus der Sonne in den Mittelpunct des Planetens gezogen wird, in gleicher Zeit gleiche Theile von der Ellipsi beschreibet, so daß der Theil von der Ellipsi ASI sich zu der ganzen Ellipsi verhält, wie die Zeit, da der Planete den Bogen AI durchläufet, zu der Zeit, da er die ganze Peripherie durchwandert. [Fig. 20]
243. Durch die Ellipsin verstehen wir eine krumme Linie, in deren Axe PA zwey Puncte S und F angenommen werden können, daraus man gegen jeden Punct in der Peripherie der Ellipsis zwey Linien ziehen kan, die so groß sind als die Axe PA. Die gedachten Puncte S und F werden die Brennpuncte genennet.
244. PERIHELIUM ist der Punct P, wo der Planete der Sonne S am nähesten ist; APHELIUM aber der Punct A, in welchem er von der Sonne am weitesten wegstehet. [Fig. 20]
245. Diejenigen, welche den Planeten mit der Sonne eine Bewegung um die Erde zueignen, nennen den Punct [462] P das Perigaeum; den Punct A aber das Apogaeum, indem sie in S die Erde setzen.
246. Die Linie PA, welche aus dem Perihelio in das Aphelium gezogen wird, heisset LINEA APSIDVM. [Fig. 20]
247. Die Weite des Brennpunctes S, wo die Sonne ist, von dem Mittelpuncte C, wird die ECCENTRICITaet genennet.
248. Die Linie SI, welche aus dem Mittelpuncte der Sonne S in die Peripherie der Ellipsis oder die Bahn des Planetens gezogen wird, heisset die Distanz oder Weite, im Lateinischen auch INTERVALLUM.
249. Die mittlere Anomalie ist die Zeit, welche der Planete zubringet, indem er von dem Apogaeo oder Aphelio A bis zu einem gewissen Puncte I in seiner Bahn fortgehet.
250. Also schicket sich zu ihrem Maasse das Stücke von der elliptischen Fläche ASI, welches die Linie, so aus der Sonne S in den Planeten I gezogen wird, währender Zeit beschrieben (§. 242.).
251. Zu dem Ende theilet Kepler, dem wir diese Theorie zu danken haben, die ganze Ellipsin in 360 gleiche Theile, und jeden Theil in 60 Scrupel, wie man den Circul einzutheilen pfleget; und durch die Theile und ihre Scrupel spricht er die mittlere Anomalie aus.
[463]252. Durch die mittlere Bewegung verstehet man diejenige, vermöge welcher der Planete in gleicher Zeit gleiche Stücke von seiner Bahn beschreibet.
253. Hingegen durch die wahre Bewegung verstehen wir diejenige, welche wir dem Planeten zueignen, indem wir auf der Erde auf ihn Achtung geben.
254. Der Eccentrische Circul ist derjenige, welcher mit der halben Axe CA durch das Aphelium A und Perihelium P beschrieben wird. [Fig. 20]
255. Die Eccentrische Anomalie ist der Bogen des Eccentrischen Circuls AK, zwischen der Linea Apsidum PA und der Linie KL, die durch den Mittelpunct des Planetens I auf die Linie PA perpendicular gezogen wird, und oben in K den Eccentrischen Circul durchschneidet, wenn man sie verlängert.
256. Die coäquirte Anomalie ist der Winkel ASI, welchen die beiden Linien, so aus dem Mittelpuncte der Sonne S in das Aphelium A und den Planeten I gezogen werden, mit einander machen, das ist, der Winkel, unter welchem der Bogen zwischen dem [464] Aphelio und dem Planeten aus der Sonne gesehen wird.
257. Daher nennet man sie auch Angulum ad Solem, oder den Winkel an der Sonne. Ihr könnet euch auch einbilden, als wenn aus A über den Fixstern ein grosser Circul beschrieben würde. Alsdenn wäre die Anomalia coaequata ein Bogen von diesem Circul zwischen dem Aphelio und dem Orte, wo der Mittelpunct des Planetens gesehen wird.
258. Die Aequation oder PROSTAPHAERESIS ist der Unterscheid der mittleren und coaequirten Anomalie.
259. Man pfleget sie auch Aequationem Centri zu nennen. Und Kepler (Epit. Astron. Copern. lib. 5. part. 2. c. 4. p. 691.) theilet sie in zwey Theile; nemlich Aequationem Opticam & Physicam. Er setzet nemlich, daß nicht allein wegen der verschiedenen Weite von der Sonne die Bewegung des Planetens ungleich erscheine, sondern auch würklich ungleich sey in seiner Bahn. Und nennet er partem aequationis physicam den Triangel CSI, oder welcher ihm gleichgültig ist, den Triangel CSK, (den er sonst Triangulum aequatorium heisset); hingegen den Winkel CIS partem opticam. Wie man alle diese Sachen finden, und dadurch die Bewegung der Planeten um die Sonne ausrechnen kan, zeige ich in den Anfangs-Gründen.
260. Weil die übrigen Planeten ausser der Erde sich nicht in der Ecliptick bewegen, sondern in einer Bahn, welche gegen die Ecliptick unter einem gewissen Winkel incliniret ist; so hat man in Ansehung ihrer noch folgende Kunstwörter nöthig.
[465]261. Die NODI oder Knoten sind die beiden Puncte der Ecliptick, in welchen die erweiterte Bahn des Planetens sie durchschneidet.
262. Die Ecliptick wird in der äussersten Fläche der Weltkugel über den Fixsternen angenommen (§. 45.). Die Bahn des Planetens wird von seinem Mittelpunct beschrieben, indem er sich um die Sonne herum beweget, und ist solchergestalt von der Ecliptick entfernet. Bildet euch aber ein, als wenn der Circul, oder vielmehr die Ellipsis, darinnen sich der Planete beweget, dergestalt erweitert würde, daß er gleichfalls bis über die Fixsterne gienge; so werdet ihr euch nicht allein besser einbilden können, als sonst, wie die Bahn des Planetens gegen die Fläche der Ecliptick incliniret ist, und sie in zwey Puncten durchschneidet; sondern auch das übrige, was von der Ausschweifung der Planeten von der Ecliptick gesagt werden soll, desto leichter verstehen.
263. Von dem einen Nodo fänget der Planete an über die Ecliptick heraufzusteigen in die nordischen Zeichen: von dem andern aber steiget er herunter in die südischen Zeichen. Jener wird Nodus ascendens, dieser descendens genennet. Zuweilen heisset auch jener Nodus Borealis; dieser aber Australis. Jenen deutet man an durch ![]() ; diesen aber durch
; diesen aber durch ![]() . In dem Mond nennet man jenen den Drachenkopf; diesen aber den Drachenschwanz.
. In dem Mond nennet man jenen den Drachenkopf; diesen aber den Drachenschwanz.

264. Die INCLINATION wird genennet der Bogen PR eines Circuls, der durch den Planeten P und die Ecliptick dergestalt aus der Sonne S beschrieben wird, daß er mit ihr in R einen rechten Winkel machet, oder [466] der Winkel an der Sonne PSR, dessen Maaß der Bogen PR ist. [Fig. 21]
265. Das Argument der INKLINATION ist der Bogen von der erweiterten Bahn des Planetens NP, welcher zwischen seinem aufsteigenden Knoten und dem Orte P, wo der Planete aus der Sonne S gesehen wird, enthalten ist. [Fig. 21]
266. Der Eccentrische Ort des Planetens ist der Punct P in seiner erweiterten Bahn, in welchem er aus der Sonne S gesehen wird.
267. Daher nennet man auch die Eccentrische Länge des Planetens den Bogen der Ecliptick NR, welcher zwischen dem ![]()
![]() und der Inclination des Planetens PR enthalten ist.
und der Inclination des Planetens PR enthalten ist.
268. Die Reduction der Ecliptick ist der Unterscheid zwischen der Eccentrischen Länge und dem Argument der Inclination.
269. Die curtirte oder verkürzte Weite des Planetens ist die Linie SR, welche zwischen dem Mittelpuncte der Sonne S und der Perpendicularlinie PR aus dem Planeten P auf der Fläche der Ecliptick enthalten ist. Der Unterscheid zwischen der curtirten Weite SR und wahren PS von der [467] Sonne S heisset die Curtirung oder Verkürzung. [Fig. 21]
270. Der heliocentrische Ort des Planetens ist der Punct der Ecliptick, wo der Planet aus der Sonne gesehen wird: der geocentrische aber, wo er von der Erde gesehen wird.
271. Der Commutationswinkel oder Winkel an der Sonne ESR ist der Unterscheid zwischen dem wahren Orte der Sonne E, wo sie nemlich von der Erde T gesehen wird, und dem zur Ecliptick reducirten Orte des Planetens R. Einige nennen sie Anomaliam Orbis. [Fig. 21]
272. Der Elongationswinkel ETR (welcher auch der Winkel an der Erde genennet wird) ist der Unterscheid zwischen dem wahren Orte der Sonne E und dem wahren Orte des Planetens, wo er von der Erde gesehen wird. [Fig. 21]
273. Die PARALLAXIS der Erdbahn ist der Winkel SRT, oder der Unterscheid zwischen dem Commutations- und Elongationswinkel. [Fig. 21]
274. Es ist abermals ein herrlicher Beweis für die Bewegung der Erde um die Sonne, daß diese Parallaxis grösser [468] ist im Marte als im Jupiter, und grösser im Jupiter als im Saturno: denn der erste ist der Erde näher als der andere, der andere aber näher als der dritte. Die Grösse der Parallaxis aber richtet sich allezeit nach der Weite (§. 125.).
275. Die Breite des Planetens ist die Weite von der Ecliptick PR, wie sie von der Erde gesehen wird, das ist der Winkel RTP. [Fig. 21]
276. Also ist der Unterscheid zwischen der Inclination und der Breite des Planetens leicht zu erachten. Jene nemlich ist der Winkel PSR, unter welchem des Planetens Abstand von der Ecliptick aus der Sonne gesehen wird: diese aber der Winket RTP, unter welchem oben dieser Abstand aus der Erde erscheinet.
277. Es scheinet nicht undienlich zu seyn, hieher zu setzen, wie die Astronomi die tägliche Bewegung der Planeten um die Sonne und des Mondes um die Erde, ihre Aphelia,, Knoten, Eccentricitates &c. in solchen Theilen, deren der Radius eccentrici 100000 hat, gefunden.
| Tägliche Bewegung der Planeten. | ||||
| 2’.11’’ | Erde | 59’8” | der | |
| 4.59 | 1°.36.8 | 13°.10’.35” | ||
| 31.27 | 4.5.32 | |||
[469]
Im Mond bewegen sich die Knoten zurücke, nemlich aus dem Widder in die Fische u. s. w. in den übrigen aber gehen sie vor sich fort, nemlich aus dem Widder in den Stier u. s. w.
278. Aus der Theorie der Bewegung der Planeten hat man durch Trigonometrische Rechnung gefunden, daß, wenn die Weite der Erde von der Sonne 10 ist, die Weite des ![]() von der
von der ![]() 4, der
4, der ![]() 7, des
7, des ![]() 15, des
15, des ![]() 52, des
52, des ![]() 95. sey.
95. sey.

279. Aus der gegebenen Parallaxi des Monds TLV und seiner Höhe KL seine Weite von der Erde zu finden. [Fig. 8]
[470]1. Da in dem Triangel TLV der Winkel L, ingleichen wegen des Winkels LVZ, dessen Maaß die Entfernung des Mondes von dem Zenith ist, der Winkel LVT (§. 38. Geom.) und der halbe Diameter der Erde TV = 1 bekannt sind; so könnet ihr die Seite TL finden (§. 20. Trig.).
2. Wenn euch die Horizontal-Parallaxis TKV gegeben wird; so ist TVK ein rechter Winkel, und ihr verfahret wie vorhin.
Z. E. die gröste Horizontal-Parallaxis TKV ist nach dem de la Hire (Tab. Astr. XVIII. p. 27.) 1° 1’ 25” und demnach
| Log. Sin. TKV | 8.2519888 |
| Log. TV | 0.0000000 |
| Log. Sin. tot. | 10.0000000 |
| Log. TK | 1.7480112 |
welchem in den Tafeln 55, das ist beynahe 56 halbe Diametri der Erde zukommen.
280. Die Weite der Sonne von der Erde zu finden.
1. Ohngefehr 6 Stunden vor dem ersten Viertel, oder 6 Stunden nach dem letzten, observiret durch ein gutes und mit einem Micrometro versehenes Fernglas den Mond, dadurch ihr ihn ganz auf einmal übersehen könnet.
2. Merket die Zeit, da der Mond halb erleuchtet ist, nach einer guten Perpendiculuhr, und messet [471] ohne Verzug seine Weite von zwey Fixsternen, deren Länge und Breite bekannt ist (§. 87.).
3. Suchet die Länge des Mondes durch die sphärische Trigonometrie, und den wahren Ort der Sonne durch die Astronomischen Tafeln.

4. Ziehet die Länge der Sonne von der Länge des Mondes ab; so bleibet die Elongation des Mondes von der Sonne DS übrig. [Fig. 22]
5. Da ihr nun bey dem in L rechtwinkelichten Triangel TLS den Winkel LTS, dessen Maaß die Elongation des Mondes ist, und eben des Mondes Weite von der Erde (§. 279.) wisset; könnet ihr die Weite der Sonne von der Erde TS finden (§. 20. Trig.). W. Z. T. W.
281. Je genauer man die Weite der Sonne zu suchen sich bemühet, je grösser kommet sie heraus, also, daß sie die alten Astronomi alle unstreitig viel zu klein ansetzen. Wendelinus hat die Weite der Sonne von der Erde 13751 halbe Diametros der Erde, und daraus ihre Paralaxin 15 Secunden gefunden, und Cassini auf seine Art nur 10 Secunden, mit welchem Flammstädt übereinkommet, da sie Ricciolus selbst noch 25 machet. Ja de la Hire setzet sie nur 6”.
282. Da ihr die Verhältniß der Weite der Planeten zu der Weite der Sonne von der Erde haben könnet (§. 278.); könnet ihr auch aller übrigen Planeten Weite von der Erde finden.
[472]283. Nach dem Cassini (wie Ozanam in seinem Cours de Mathematique Tom. Trait. de Geogr. part. 1. c. 2. p. 64. 65. berichtet) sind die Weiten der Planeten und der Sonne von der Erde in halben Diametern der Erde in folgender Grösse:
| Gröste | Mittlere | Kleineste | |
| Weite. | Weite. | Weite. | |
| 244000 | 210000 | 176000 | |
| 143000 | 115000 | 87000 | |
| 59000 | 33500 | 8000 | |
| 22374 | 22000 | 21626 | |
| 38000 | 22000 | 6000 | |
| 33000 | 22000 | 11000 | |
| 61 | 57 | 53 |
Aus des de la Hire Sonnen-Parallaxi kommen sie noch grösser heraus, wie ich in meinen Elementis Astronomiae zeige.

284. Aus der gegebenen Weite eines Sternes von der Erde TK; oder TS, seine Horizontal-Parallaxin TKV, imgleichen seine Parallaxin TSV in einer gegebenen Höhe zu finden. [Fig. 8]
In dem bey V rechtwinkelichten Triangel TKV könnet ihr aus den beiden Seiten TK und TV den Winkel TKV; ingleichen im Triangel TSV aus dem Winkel STV und den beiden Seiten TS und TV den Winkel TSV (§. 23. 28. Trigon.) finden.
[473]285. Aus der gegebenen Weite eines Sternes von der Erde und seinem scheinbaren Diameter den wahren Diameter zu finden.

In dem bey A rechtwinkelichten Triangel ACO wisset ihr den Winkel O, als den scheinbaren halben Diameter, und die Weite des Sternes CO. Derowegen könnet ihr seinen wahren halben Diameter AC (§. 20. Trigon.) finden. [Fig. 11]
Z. E. es sey die geringste Weite des Mondes CO 55 (§. 279.) und AOC nach dem de la Hire (Tab. Astron. XVII. p. 27.) 16’ 30”; so ist
| Log. Sin tot. | 10.0000000 | |
| CO | 1.7480112 | |
| Sin. AOC | 7.6812083 | |
| 9.4292195 | ||
| Log. AC | -0.5707805, | |
welchem in den Tafeln am nächsten kommen.
Demnach ist der Diameter des Mondes oder (§. 84. Arithm.) von dem Diameter der Erde.
286. Weil der Diameter der Erde sich zu dem Diameter des Mondes verhält wie 250 zu 67 (§. 59. Arithm.); so verhält sich die Fläche der Erde zu der Fläche des Mondes, wie 62500 zu [474] 4489 (§. 131. Geom.); hingegen die ganzen Körper verhalten sich gegen einander wie 15625000 zu 300763 (§. 212. Geom.).
287. Derowegen ist die Fläche der Erde beynahe 14mal so groß, als die Fläche des Mondes: hingegen die ganze Erde ist beynahe 52mal so groß, als der Mond (§. 52. Arithm.).
288. Da nun unsere Erde das Sonnenlicht, damit sie bestrahlet wird, eben so wohl als der Mond zurücke wirfet; so muß sie 14mal so viel Licht in den Mond, als der Mond auf die Erde werfen.
289. Daher ist nicht zu zweifeln, daß das schwache Licht, welches man um den Neumond in dem von der Sonne weggekehrten Theile des Mondes stehet, von der Erde sey, indem es dem erleuchteten Theile der Erde entgegengesetzet ist.
290. Wie der Erddiameter sich zu dem Diameter der übrigen Planeten, und seine Grösse in ihrer Grösse verhält, ist aus beygefügtem Täfelein zu ersehen.
[475]

291. Aus dem halben Diameter des Monds AC und der Weite der Spitze eines Berges, die erleuchtet wird, von dem erleuchteten Theile des Mondes AB, die Höhe desselben Berges zu finden. [Fig. 12]
1. Addiret die Quadrate von AB und AC.
2. Aus der Summe ziehet die Quadratwurzel (§. 77. Arithm.); so habet ihr BC (§. 144. Geom.).
3. Ziehet von BC den halben Diameter des Mondes DC ab; so bleibet die Höhe des Berges BD übrig.
Z. E. in einigen Bergen ist AB = AE (§. 184.). Wenn ihr nun AC 67 oder AE 134 dergleichen Theile gebet, als der halbe Diameter der Erde 250 hat, (§. 286.); so ist AB = 5 [476] (§. 85. Arithm.), folgends zu AC wie 5 zu 67, oder wie 67 zu 871.
| AC² = 758641 | BC = 873 | |
| AB² = 4489 | DC = 871 | |
| BC² = 763130 | BD = 2. |
Nehmet ihr nun ferner den halben Diameter der Erde, wie insgemein geschiehet, 860 deutsche Meilen an; so findet ihr AC 231 Meilen, oder beynahe 482 halbe Meilen (§. 85. Arithm.), und endlich, da sich BD zu AC wie 2 zu 871 verhält, BD etwas über eine halbe deutsche Meile.
292. Da man die Höhe der Berge im Monde mit solcher Gewißheit ausrechnen kan; dürfet ihr euch um so viel weniger befremden lassen, daß man jeden Berg und jedes Meer mit seinem besondern Namen nennen kan. Hevel hat die Namen der Gebürge und Meere auf unserer Erde angenommen, und sie denen im Monde gegeben, weil er eine Gleichheit zwischen der Charte über den Mond und der Charte über die halbe Erdkugel bemerket (Selenograph. c. 8. f. 225. &seqq.). Ricciolus hat nach Langreni Exempel den Bergen und Flecken Namen der Personen gegeben. (Almag. Nov. lib. 4. c. 7. f. 204. & Astron. Reform. lib. 3. c. II. f. 168.) Es hat aber die Charte über den Mond einen grossen Nutzen in Observirung der Mondfinstenisse.
293. Den scheinbaren Diameter der Erde im Monde zu finden, das ist, den Winkel, unter welchem die Erde im Monde gesehen wird.
[477]Wenn der halbe Diameter der Horizontal-Parallaxi des Mondes gleich ist; so habet ihr nur nöthig, diese zu suchen (§. 284.). Da sie nun in der geringsten Weite 1° 1’ 25” hält; so ist der scheinbare Diameter der Erde im ![]() niemals grösser als 2° 3’ oder 123’.
niemals grösser als 2° 3’ oder 123’.
294. Daher siehet der Diameter der Erde beynahe viermal so groß im Monde aus, als der Diameter des Mondes auf der Erde.
295. Weil aber die Erde unter einem so kleinen Winkel im Monde gesehen wird; so kan man nichts deutlich davon sehen (§. 26. Optic.). Und daher stellet sie sich den Seleniten nicht anders als ein runder hellleuchtender Teller vor.
296. Solchergestalt siehet die Erde den Seleniten eben so wie uns der Mond aus, und wird dannenhero mit Recht von ihnen, wie von uns der Mond, unter die Zahl der Sterne, und zwar der Planeten gesetzet. Denn sie ist ein Körper, welcher ihnen des Nachts am Himmel leuchtet.
297. Ihr könnet leicht erachten, daß, wenn die Erde aus einem Planeten gesehen wird, der weiter von ihr weg ist, als der Mond, sie auch viel kleiner aussehen müsse (§. 23. Optic.), und also in einigen Orten auch würklich wie ein Stern erscheine.
[478]298. Hugenius in seinem Cosmotheoro lib. 2. p. m. 114. merket an, daß durch die vortrefflichsten Ferngläser die Fixsterne nur wie ein heller Punct ohne alle Breite erscheinen.
299. Daher haben wir keinen gewissen Grund, daraus wir ihre wahre Grösse ermessen können.
300. Die Fixsterne können ihr Licht nicht von der Sonne haben.
Sie sind weiter von der Senne weg, als Saturnus (§. 217.): und doch ist ihr Licht viel heller, wird auch nicht schwächer, als das Licht der Planeten, wenn man sie durch Ferngläser ansiehet. Derowegen können sie es nicht von der Sonne haben. W. Z. E.
301. Also haben sie ihr eigenes Licht, und sind demnach lauter Sonnen.
302. Daher ist glaublich, daß sie auch ihre Planeten haben, die sich um sie bewegen. Woraus denn eine unendliche Grösse des Weltgebäudes entspringen, und eine unzählige Zahl der vernünftigen Creaturen, die ihren Schöpfer loben.
303. Eben so hat man Ursache zu glauben, es sey Sirius nicht kleiner, als die Sonne: und hierauf hat sich Hugenius gegründet, als er in seinem Cosmotheoro p. 115. die Weite der Fixsterne von der Erde einiger massen ermessen wollen, welche [479] er 27664 mal grösser, als die Weite der Sonne von der Erde setzet.
304. Zuweilen erscheinen einige Sterne, die man vorhin nicht sahe; über eine Weile verschwinden sie, und zu anderer Zeit kommen sie wieder. Dergleichen Stern ist auf der Brust des Schwanes, welcher von den Astronomis Mira oder der Wunderbare genennet wird. Andere hingegen kommen nicht mehr wieder, wenn sie sich einmal sehen lassen. Dergleichen ist der Stern, welcher zu Tychonis Zeiten in dem Gestirne der Cassiopejae erschien, viel grösser und heller als alle übrige Sterne, so daß er auch des Nachts durch die Wolken, und des Tages bey hellem Sonnenschein von scharfen Augen gesehen wurde. Seine Grösse und Helle nahm nach und nach ab, bis er endlich ganz verschwand. Vid. Tycho Progymnasm. Tom. 1. c. 3. & seqq.
305. Die Sterne, welche bald erscheinen, bald verschwinden, sind vielleicht einige Planeten, die sich um die Fixsterne als ihre Sonnen bewegen (§. 302.); wiewohl ihr starkes Licht entgegen zu seyn scheinet, und man also nichts zuverläßiges bestimmen kan.
306. Unter den Sternen, die sich nur zuweilen sehen lassen, haben einige eine Bewegung [480] in Ansehung der Fixsterne, und öfters einen langen Schweif. Dieselben werden Cometen genennet. Sie bewegen sich über dieses auch wie das ganze übrige himmlische Heer in 24 Stunden um unsere Erde. Nach ihrer eigenen Bewegung aber folgen sie nicht wie die Planeten den Zeichen des Thierkreises: sondern gehen wol von Mittage gegen Norden. Durch gute Ferngläser haben sie Heveln (Cometogr. lib. 8. f. 476.) wie unsere Wolken ausgesehen. Und da Weigel A. 1664. den Cometen zugleich mit dem Monde und einem Wölklein, so von der Sonne am Abendhorizont erleuchtet wurde, durch ein Fernglas betrachtete, nahm er wahr, daß das Licht des Mondes in einem fortging, das Licht der Wolken und des Cometens aber überall unterbrochen war. Es sahe das Licht des Mondes gegen das Licht der Wolken und des Cometens aus, wie eine ebene polirte Fläche gegen eine andere, die hin und wieder kleine Grüblein hat. Vid. die Fortsetzung des Himmelsspiegels c. II. §. 5. p. 96. Die Köpfe der Cometen sehen in der Mitten dichter aus, als um den Rand; welchen mittleren Theil man den Kern nennet. Dieser Kern wird nach und nach kleiner, zerfähret in viele Stücke, ja endlich gar in eine Materie, die der übrigen gleich siehet. Vid. Hevelii Cometogr. lib. 9. f. 562. & lib. 7. f. 409. Es [481] ist aber der Kopf der Cometen A. 1665. und 1680. ganz erleuchtet gewesen, als sie nur 22 bis 23 Grad von der Sonne wegstunden. Der Schweif hingegen ist so dünne, daß man die Firsterne dadurch sehen kan, wie Hevel Cometogr. lib. 8. f. 516. & 517. anmerket, und der Sonne jederzeit entgegengesetzet. Die Bewegung der Cometen ist überaus ordentlich, wie der Planeten, ob sie zwar einen besondern Thierkreis haben, den Cassini in folgende Verse eingeschlossen:
Antinous, Pegasusque, Andromeda, Taurus, Orion,
Procyon atque Hydrus, Centaurus, Scorpius, Arcus.
Auch hat man befunden, daß der Comet, welchen Tycho A. 1577. observiret, eben so geschwinde und in eben dem Wege sich beweget, wie der, welcher A. 1680 erschien. Den letzteren hat man noch durch ein Fernglas erblicket, da er mir blossen Augen nicht mehr gesehen wurde.
307. Weil die Cometen die erste Bewegung um die Erde mit dem ganzen himmlischen Heere gemein haben; so können sie sich nicht in der Luft aufhalten, wie Aristoteles geglaubet, sondern müssen in dem Himmel unter den Planeten, oder über denselben seyn.
[482]308. Da sie aber sonderlich durch Ferngläser bloß wie eine von der Sonne erleuchtete Wolke aussehen; so ist glaublich, daß sie für sich kein Licht haben, sondern es wie die Planeten von der Sonne bekommen.
309. Derowegen, da die Cometen A. 1664. und A. 1683. ganz erleuchtet waren, wie sie von der Sonne nur 22° wegstunden: so müssen sie über der Sonne gewesen, das ist, weiter von der Erde gestanden seyn, als die Sonne.
310. Da nun der Schweif von der Sonne erleuchtet wird, unerachtet er hinter dem Kopfe des Cometens, und also in seinem Schatten stehet; so muß das Sonnenlicht durch des Cometens Kopf durchfallen können, oder es müste innerhalb dem Cometen ein Licht seyn.
311. Der Schweif muß aber einem dünnen Nebel gleichen, weil sich die Sterne dadurch sehen lassen.
312. Weil die Cometen eine so ordentliche Bewegung haben, auch wieder kommen; so müssen sie beständige Weltkörper seyn.
313. Kepler hält sie für Himmelswolken, die in der subtilen Himmelsluft erzeuget würden; welche Meinung absonderlich Hevel in seiner Cometographia ausführet.
[483]314. Es mögen aber die Cometen entweder Weltkörper seyn, die von GOtt im Anfange der Welt erschaffen worden, oder auch aus den Ausdünstungen der Planeten, oder auf andere Weise von neuem entstehen; so kan man daher nicht erweisen, daß sie den Inwohnern der Erde entweder etwas Gutes oder etwas Böses bedeuten, wenn Sie von ihnen gesehen werden. Denn in beiden Fällen hätte der Schluß keinen richtigen Grund. Ja in der Bibel hat sich GOtt nirgends erkläret, daß er die Cometen zum Zeichen seines Zorns oder auch seiner Gnade gesetzet. Vielmehr hat er uns warnen lassen, daß wir uns für den Zeichen des Himmels nicht fürchten sollen, wie die Heiden, Jer. 10. Und es wäre auch ungereimt, daß die Cometen Boten des göttlichen Zorns seyn solten, da die meisten von den wenigsten Menschen gesehen werden: wie denn von A. 1699. an bis 1709. fast alle Jahre, aber nur von wenigen Astronomis bey nächtlicher Weile Cometen gesehen worden. Vid. Histoire de l’Academie Royale des Sciences A. 1699. 1700. 1701. &c. Aus der Erfahrung kan man nicht schliessen, daß die Cometen eine böse Bedeutung haben. Denn es ist keine Folge: auf die Erscheinung des Cometens ist einer gewissen Nation ein grosses Unglück begegnet, derowegen hat der Comete dieses bedeutet. Zu geschweigen, daß man aus der Historie nicht erweisen kan, es sey jederzeit auf die Erscheinung eines Cometens eine grosse Veränderung in den Reichen der Welt erfolget. Ja, wenn GOtt einem gewissen Volke durch ein Zeichen vom Himmel seinen Untergang ankündigen wolte; müste er es in unsere Luft setzen, daß es über dem Lande oder der Stadt stehen bliebe, dem der Untergang angedeutet wird: wie man von dem Cometen erzählet, der über Jerusalem durch das ganze jüdische Land vor der Verstöhrung gesehen ward.
315. Wenn der Planete mit der Sonne in einem Orte des Himmels gesehen wird, oder von ihm um den sechsten, vierten, dritten, oder halben Theil des Himmels wegstehet, so nennet man es einen Adspect, und zwar insbesondere in dem ersten Falle eine CONJUNCTION [484] oder Zusammenkunft; in dem anderen den Gesechstschein (Sextilem); in dem dritten den Geviertschein (Quadratum); in dem vierten den Gedrittschein (Trigonum); und in dem letzten die Entgegensetzung oder OPPOSITION.
316. Die Zeichen, damit sie bemerket werden, sind folgende: ![]()
![]()
![]()
![]()
![]() . Z. E. wenn Saturnus und Jupiter im Geviertscheine gegen einander stehen, schreibet man
. Z. E. wenn Saturnus und Jupiter im Geviertscheine gegen einander stehen, schreibet man ![]()
![]()
![]() . Hingegen wenn das Zeichen des Adspects nur zu Einem Planeten gesetzt wird, verstehet man zugleich mit dabey den Mond. Also bedeutet
. Hingegen wenn das Zeichen des Adspects nur zu Einem Planeten gesetzt wird, verstehet man zugleich mit dabey den Mond. Also bedeutet ![]()
![]() den Gesechstschein der
den Gesechstschein der ![]() mit dem
mit dem ![]() , das ist, daß der Mond von der
, das ist, daß der Mond von der ![]() 60° wegstehet.
60° wegstehet.
317. Die Conjunction des ![]() und
und ![]() wird die grosse CONJUNCTION genennet, ja gar die größte CONJUNCTION, wenn sie im Anfange des Widders geschiehet, welches sich alle 794 Jahre einmal zuträget, da die grossen beynahe nach 20 Jahren wieder kommen. Die Astrologi haben ihnen diese Benennung zugeleget, weil sie selbige von grosser Würkung zu seyn erachtet: wie denn sie das ganze Wesen mit den Adspecten auf die Bahn gebracht, und daher nicht allein die Ursachen der Witterung auf unserem Erdboden, sondern auch andere Einflüsse in die Körper auf der Erde, ja den Menschen selbst, herholen wollen. Allein da man weder aus der Natur des Adspectes, noch durch gegründete Erfahrung einigen Einfluß behaupten kan: so haben heute zu Tage alle verständige Astronomi diesen albern Kram verlassen. Es ist allerdings kein Schluß: Saturnus stehet von dem Jupiter 90° weg in Ansehung unserer Erde, derowegen muß eine Veränderung des Wetters oder auch in den Körpern auf dem Erdboden erfolgen. Eben so wenig schliesset es: heute ist der Adspect gewesen, das ist, der oder jener Planete hat uns auf der Erde 60, 90, 120 oder 180° von einem
[485] andern weg zu stehen geschienen, und es hat geregnet; derowegen ist die Ursache des Regens gewesen, daß sie uns so weit von einander zu stehen auf der Erde geschienen. Keine ander Erfahrung, als diese, kan jemand anführen.
wird die grosse CONJUNCTION genennet, ja gar die größte CONJUNCTION, wenn sie im Anfange des Widders geschiehet, welches sich alle 794 Jahre einmal zuträget, da die grossen beynahe nach 20 Jahren wieder kommen. Die Astrologi haben ihnen diese Benennung zugeleget, weil sie selbige von grosser Würkung zu seyn erachtet: wie denn sie das ganze Wesen mit den Adspecten auf die Bahn gebracht, und daher nicht allein die Ursachen der Witterung auf unserem Erdboden, sondern auch andere Einflüsse in die Körper auf der Erde, ja den Menschen selbst, herholen wollen. Allein da man weder aus der Natur des Adspectes, noch durch gegründete Erfahrung einigen Einfluß behaupten kan: so haben heute zu Tage alle verständige Astronomi diesen albern Kram verlassen. Es ist allerdings kein Schluß: Saturnus stehet von dem Jupiter 90° weg in Ansehung unserer Erde, derowegen muß eine Veränderung des Wetters oder auch in den Körpern auf dem Erdboden erfolgen. Eben so wenig schliesset es: heute ist der Adspect gewesen, das ist, der oder jener Planete hat uns auf der Erde 60, 90, 120 oder 180° von einem
[485] andern weg zu stehen geschienen, und es hat geregnet; derowegen ist die Ursache des Regens gewesen, daß sie uns so weit von einander zu stehen auf der Erde geschienen. Keine ander Erfahrung, als diese, kan jemand anführen.
318. Wenn der Mond in seiner Opposition entweder in dem Knoten, oder nahe dabey anzutreffen ist: so wird er verfinstert.
Wenn der Mond im Knoten ist, so stehet sein Mittelpunct in der Ecliptick; hält er sich aber nahe bey dem Knoten auf, so ist er auch der Ecliptick nahe (§. 261.). Nun wird er verfinstert von dem Erdschatten, wenn er der Sonne entweder in der Ecliptick, oder nahe bey derselben, entgegengesetzet ist (§. 155.). Derowegen ist eine Mondfinsterniß, wenn der Mond entweder im Knoten, oder nahe dabey voll wird. W. Z. E.
319. Es ist also in einer Mondfinsterniß die Summe aus dem halben scheinbaren Diameter des Mondes und des Erdschattens grösser, als seine Breite.
320. Hieraus erhellet, warum nicht alle Vollmond eine Mondfinsterniß ist; imgleichen warum eine Finsterniß grösser ist, und länger dauret, als die andere.
321. Eine Mondfinsterniß zu observiren.
[486]1. Stellet eine Perpendiculuhr nach der Sonne (§. 32.), oder corrigiret die Zeit, die ihr darnach angemerket, aus observirten Höhen der Sterne.
2. Richtet ein Fernglas mit einem Micrometro gegen den Mond, und merket die Zeit, wenn seine Peripherie die Rundung zu verlieren beginnet; so wisset ihr den Anfang der Finsterniß.
3. Merket gleichfalls die Zeit, da der Erdschatten die aus der Mondbeschreibung bekannten Flecken erreichet, imgleichen da er den ganzen Mond verlässet; so sehet ihr, wie die Finsterniß von Zeit zu Zeit zu- und abgenommen, und wenn sie aufhöret.
4. Ziehet das Ende von dem Anfange ab; so wisset ihr, wie lange sie gewähret: welche Zeit, in zwey Theile getheilet, das Mittel der Finsterniß bekannt machet.
5. Durch Hülfe des Micrometri messet die Grösse des verfinsterten Diametri (§. 182.).
322. Die auf dem Erdboden eine Sonnenfinsterniß sehen, stehen entweder im Schatten oder Halbschatten des Mondes.
Wir sehen eine Sonnenfinsterniß, wenn uns der Mond die Sonne decket (§. 149.). Denen [487] nun, die im Schatten des Mondes, oder in seinem Halbschatten stehen, wird die Sonne wenigstens zum Theil verdecket, nemlich um so viel mehr, je näher sie dem Schatten sind. Derowegen sehen sie eine Sonnenfinsterniß. W. Z. E.
323. Da nun der Schatten des Mondes der Sonne gegen über geworfen wird, die Erde aber den der Sonne entgegengesetzten Ort in der Ecliptick einnimmet (§. 235.); so muß der Schatten und Halbschatten des Mondes gegen die Ecliptick fallen, wenn auf dem Erdboden eine Sonnenfinsterniß sich begeben soll, und demnach der Neumond entweder in dem Knoten, oder sehr nahe dabey seyn (§. 261.).
324. Derowegen sehen die Seleniten eine Erdfinsterniß, wenn wir eine Sonnenfinsterniß haben.
325. Der Halbschatten ist in dem Orte, wo nicht von allen Theilen der Sonne Strahlen hinfallen können.
326. Eine Sonnenfinsterniß zu observiren.
1. Fanget in einem verfinsterten Gemache das Bild der Sonne, welches ihr durch ein Fernglas hineinfallen lasset, mit einem weissen Papiere auf, und theilet es in seine 12 Zolle. Nemlich der [488] halbe Diameter wird in 6 gleiche Theile getheilet, und durch jeden Theilungspunct wird aus dem Mittelpuncte ein Circul gezogen.
2. Merket vermittelst einer richtig gestellten Perpendiculuhr die Zeit an, da die Finsterniß sich anfänget und aufhöret, auch ein jeder Zoll verfinstert erscheinet und wieder helle wird.
3. Corrigiret die Zeit, wenn die Uhr nicht recht gehet, aus den observirten Höhen der Sonne, oder durch Hülfe der Mittagslinie.
Anmerkungen (Wikisource)
- ↑ Das Symbol für Schütze (Sagittarius) ist im Orginal ein vertikaler Pfeil nach oben.
- ↑ im Original: Ferngälser
- ↑ vgl. Philippe de La Hire
- ↑ vgl. Tycho Brahe
















