Auszug aus den Anfangs-Gründen aller Mathematischen Wissenschaften/Die Mechanick
Die Bewegungs-Kunst oder Mechanick ist eine Wissenschaft, entweder mit Vortheil der Kraft, oder der Zeit etwas zu bewegen, das ist, eine grössere oder geschwindere Bewegung hervorzubringen, als sonst der gegebenen Kraft von sich möglich wäre.
2. Die Bewegungs-Kunst (Mechanica) handelt zwar eigentlich von allen Gesetzen der Bewegung, wie auch einige dieselbe in ihren mechanischen Schriften zu erklären sich bemühen. Insgemein aber redet man in der Mechanick nur von den Maschinen, dadurch die bewegende Kraft entweder vermögender gemacht wird, eine grössere Last als sonst zu bewegen, oder die Bewegung geschwinder als sonst zu verrichten.
3. Alles, was die Bewegung verursachet, nennen wir eine Kraft; was aber beweget wird, oder der Bewegung widerstehet, eine Last.
4. Daher werden sowohl die lebendigen, als leblosen Creaturen, unter die bewegenden Kräfte gerechnet, [194] deren man sich, eine Bewegung hervorzubringen, bedienet, als Menschen, Vieh, Luft, Wasser, Feuer, Gewichte, Federn.
5. Da nun die Mechanick lehret, wie man mit einer gegebenen Kraft eine vortheilhafte Bewegung hervorbringen kan (§. 1.); so muß darinnen auch gezeiget werden, wie man sich der Menschen, der Thiere, der Luft, des Wassers, des Feuers, der Gewichte, der Federn zu vortheilhaften Bewegungen bedienen kan.
6. Wenn die Bewegung wirklich geschiehet, heisset es eine lebendige Kraft; wenn aber die Last nur erhalten wird, nennet man es eine todte, oder auch eine erhaltende Kraft.
7. Dasjenige, so die Kraft vermögend machet, eine vortheilhafte Bewegung hervorzubringen, nennet man eine Maschine.

8. Der Hebel ist eine gerade steife Linie AB, so in einem Puncte C auflieget, an deren einem Puncte B die Kraft, an einem andern A aber die Last appliciret werden kan.[Fig.1]
9. Es ist hier überhaupt zu merken, daß, wenn man das Vermögen des Rüstzeuges untersuchet, man Anfangs die Materie, daraus es bestehet, und die Eigenschaften der Materie, wie auch die äussere Figur, welche der Rüstzeug gewisser Umstände wegen bekommet, aus den Augen setzet, und nur dasjenige [195] betrachtet, was ihn zu einem Rüstzeuge machet, damit man weiß, was ihm als enenm Rüstzeuge zukommet. Hindert hernach die Materie, daraus er bestehet, sein wesentliches Vermögen, so ist solches insbesondere auszumachen.
10. Wo ihr euch also bey einer Bewegung drey Puncte einbilden könnet, um deren einen die Bewegung geschiehet, an dem andern die Kraft, an dem dritten aber die Last appliciret ist; daselbst treffet ihr einen Hebel an.
11. Wenn ihr dieses wohl merket; so werdet ihr aus den Gesetzen des Hebels nicht allein von den meisten Instrumenten und andern Werken der Kunst, sondern auch von den wunderbaren Bewegungen in den Körpern der Thiere und der Menschen richtigen Grund zeigen, und beiderseits ihr Vermögen ausrechnen können. Auf diesem Grunde beruhet, was Borellus von der Bewegung der Thiere geschrieben.

12. Ein Rad an einer Axe (Axis in peritrochio) ist nichts anders, als ein an einer Welle befestigter Circul AFDA, welcher zugleich mit der Welle BIKB um ihren gemeinen Mittelpunct C beweget werden kan. Ja es ist genug, wenn man sich einen Circul nur gedenken kan, der in der Bewegung der Welle um ihre Axe beschrieben wird.[Fig.2]

13. Ihr treffet demnach ein Rad an einer Axe an, wo ihr euch gedenken könnet, daß ein grösserer Circul, als der Durchschnitt einer Welle ist, beschrieben werde, wenn sie sich um ihre Axe beweget.[Fig.3] Z. E. im mechanischen Verstande gehören [196] die gewöhnlichen Winden FGHI mit unter die Räder an einer Axe, weil die Stange IH, die in der Bewegung der Welle um ihre Axe FG fortgestossen wird, einen Circul beschreibet (§. 11. Geom.).
14. Wenn es zu der Ausübung kommet, müssen die Räder auf verschiedene Art verfertiget werden, nachdem entweder die Kraft ist, welche an sie appliciret wird, oder nachdem sie die Bewegung einem andern Theile mittheilen sollen.


15. Wenn ein Rad anderswo eingreiffen soll, wird es mit Zähnen oder Kammen besetzet, entweder oben an der Stirne,[Fig.5] oder nur zu der Seiten unweit der Peripherie.[Fig.4] In dem ersten Falle nennet man es ein Stirn-Rad oder Stern-Rad; in dem andern aber ein Kamm-Rad.
16. Dasjenige Rad, welches beweget wird, indem ein anders mit seinen Kammen in dasselbe eingreiffet, wird das Getrieb genennet.
17. Wenn es aus zwey Scheiben KL und MN zusammengesetzet wird, und anstatt der Kammen cylindrische Stöcke eingeschlagen werden, pfleget man es auch einen Trilling zu nennen.

18. Ein Circul, oder eine Scheibe AB, die um ihren Mittelpunct C beweget wird, [197] wenn die Kraft in D das Gewichte E in die Höhe ziehet, wird eine Rolle oder Scheibe des Klobens (Trochlea) genennet.[Fig.6]

19. Eine schiefliegende Fläche AC wird genennet, welche mit der Horizontallinie BC einen schiefen Winkel ACB machet.[Fig.7]

20. Wenn dergleichen Fläche um eine Welle IK im Kreise herumgeführet wird, entstehet eine Schraube: die Welle aber, darum sie geführet wird, nennet man die Spindel.[Fig.8]
21. Eine Schrauben Muttern LM wird genennet, welche ihre Gänge inwendig in der Fläche einer ausgehöleten Welle hat.[Fig.8]
22. Der Punct C, um welchen sich die Maschine bewegen kan, wird der Ruhepunct oder auch der Bewegungspunct genennet.[Fig.1]
23. Die Directionslinien (Linea directiones) ist eine gerade Linie, nach welcher die Kraft und die Last entweder wirklich beweget werden, oder sich bewegen würden, wenn nicht etwas die Bewegung hinderte.[Fig.1] Z. E. Wenn das Gewichte O nach der Linie AO herunter fallen würde, wenn man es in A abschneiden solte; so heisset die Linie AO seine Directionslinie. Wiederum, wenn [198] eine Kraft in H nach der Linie HB ziehet; so ist gleichfals HB ihre Directionslinie.
24. Die Entfernung (nemlich von dem Ruhepunct) ist eine Linie CD, welche aus dem Ruhepuncte C auf die Directionslinie BH perpendicular gezogen wird.[Fig.1]
25. Also haben die Kraft und die Last die gröste Entfernung, wenn sie unter einem rechten Winkel an die Maschine appliciret werden. Denn wenn die Directionslinie BE mit der Maschine AB einen rechten Winkel machet; so ist die Entfernung CB. Machet sie aber einen schiefen Winkel CBH; so ist die Entfernung CD. Nun ist aber in dem rechtwinkelichten Triangel CBD die Linie CB grösser als CD (§.144. Geom.).
26. Der Mittelpunct der Schwere (Centrum gravitatis) ist derjenige, dadurch ein Körper in zwey gleichwichtige Theile getheilet wird.
27. Der Mittelpunct der Grösse (Centrum magnitudinis) ist derjenige, dadurch ein Körper in zwey gleichgrosse Theile getheilet wird.
28. Die Horizontallinie ist diejenige, in welcher ein jeder Punct von dem Mittelpuncte der Erde gleich weit weg ist.
[199]29. Die Horizontal-Linie ist eigentlich ein Circulbogen, der aus dem Mittel-Puncte der Erde beschrieben wird (§. 13. Geom.).

30. Allein weil die Sehnen kleiner Bogen, sonderlich in grossen Circuln, mit den Bogen beynahe übereinkommen, oder nicht merklich von ihnen unterschieden sind (§. 126. Geom.); so kan man die gerade Linie MP, welche die wahre Horizontallinie in dem gegebenen Orte C berühret, für die Horizontallinie annehmen.[Fig.9]
31. Die gerade Linie MP, welche die wahre Horizontallinie in einem gegebenen Punkte C berühret, wird die scheinbare Horizontallinie genennet.[Fig.9]
32. Die Schwere ist eine Kraft, durch welche der Körper gegen den Mittelpunct der Erde getrieben wird.

33. Wenn ein Körper DE dergestalt aufgehänget wird, daß die Linie, nach welcher man ihn aufhänget, AB durch seiner Schwere Mittelpunct gehet, oder er auch in dem Mittelpunct der Schwere auflieget; so hänget oder lieget er stille.[Fig.10]
Denn weil derselbe durch den Mittelpunct der Schwere in zwey gleichwichtige Theile getheilet [200] wird (§. 26.); so drucket auf der einen Seite der Theil E so viel darnieder, als auf der andern der Theil D. Und dannenhero ist keine Ursache, warum eher der Theil D, als der Theil E gehoben werden solte. Derowegen kan keiner gehoben werden, und solchergestalt hanget oder lieget der Körper stille. W. Z. E.
34. Was demnach den Mittelpunct der Schwere unterstützet, das träget die Schwere des ganzen Körpers.
35. Und darum kan man sich einbilden, als sey die ganze Schwere in dem einigen Mittelpuncte der Schwere bey einander.
36. Wenn ein Körper durchaus aus einerley Materie bestehet, und einerley Breite und Dicke behält; so kommet der Mittelpunct der Schwere mit dem Mittelpuncte der Grösse überein.
Denn in diesem Falle ist keine Ursache, warum Theile gleicher Grösse nicht gleichwichtig seyn solten, und daher sind sie gleichwichtig. Da nun der Körper durch den Mittelpunct der Grösse in zwey gleichgrosse (§. 27.), durch den Mittelpunct der Schwere aber in zwey gleichwichtige Theile (§. 26.) getheilet wird: so muß der Mittelpunct der Schwere mit dem Mittelpuncte der Grösse übereinkommen. W. Z. E.
[201]37. Den Mittelpunct der Schwere in einem jedem Körper zu finden.

1. Schiebet den Körper HI auf einer ausgespanneten Saite, oder einem scharfschneidigen dreyeckigten Prismate FG so lange hin und wieder, bis er drauf stille liegen bleibet; so ist der Linie LK, wo er auflieget, der Mittelpunct der Schwere (§. 34).[Fig.11]
2. Wenn ihr ihn nun auf eben dieses Seil oder Prisma gleichergestalt nach einer andern Linie MN auflegt; so ist abermals in derselben der Mittelpunct der Schwere (§. 34), folgendes in O, wo die beiden Linien einander durchschneiden.
Unterweilen könnet ihr den Mittelpunct der Schwere finden, wenn ihr den Körper auf einem spitzigen Stifte hin und wieder verschiebet, z. E. einen Teller auf der Spitze einer Gabel.
38. Wenn die Directionslinie innerhalb den Grund fället, darauf der Körper ruhet; so muß er stille liegen und kan nicht fallen. So bald sie aber ausserhalb diesen Grund verrücket wird, muß er gegen die Seite fallen, wo die Directionslinie von dem Grunde ausweichet.
Die Directionslinie ist eine gerade Linie, nach welcher sich der Körper in einem gegebenen Falle [202] entweder würklich beweget, oder bewegen würde, wenn nichts seine Bewegung hinderte (§. 23.). Fället nun diese innerhalb den Grund des Körpers, darauf er ruhet; so kan der Körper sich nach dieser Linie nicht bewegen. Daher muß er stille liegen oder stehen. Welches das erste war.
Hingegen wenn die Directionslinie ausserhalb den Grund des Körpers fället; so hindert nichts, daß er sich nicht nach derselben bewegen könte. Und dannenhero muß er fallen. Welches das andere war.
39. Je breiter der Grund ist, darauf der Körper ruhet, je mit grösserer Mühe kan er umgeworfen werden: denn die Directionslinie muß durch einen grossen Raum bewegt werden, ehe sie ausserhalb den Grund verrücket wird.

40. Die gerade Linie MP, welche den Circul in C berühret, machet mit dem Radio CL einen rechten Winkel in dem Berührungs-Puncte C.[Fig.9]
Wenn die Linie CL auf MP nicht perpendicular stehet; so kan man aus L eine andere Perpendicularlinie auf MP ziehen (§. 69. Geom.). Es sey dieselbe LP. Weil nun P ein rechter Winkel ist; so muß LC grösser als LP seyn (§. 144. Geom.). Es ist aber LC = LN (§. 27. Geom.). Folgends ist LN grösser als LP. Da nun dieses ungereimt ist; so muß bey C ein rechter Winkel seyn. W. Z. E.
[203]41. Die Directionslinie der schweren Körper stehet auf der scheinbaren Horizontallinie perpendicular.
Die schweren Körper fallen vermöge ihrer Schwere nach dem Mittelpuncte der Erde (§. 32.), und also kommet ihre Dircetionslinie mit dem Radio der Erdkugel CL überein (§. 23. Mech. & §. 13. Geom.). Die scheinbare Horizontallinie MP berühret die Peripherie der Erde in C (§. 31.). Derowegen machet die Directionslinie der schweren Körper mit der scheinbaren Horizontallinie einen rechten Winkel (§. 40.); und stehet demnach auf derselben perpendicular (§. 18. Geom.).[Fig.9] W. Z. E.
42. Weil die Schwere des ganzen Körpers in dem Mittelpuncte der Schwere bey einander ist (§. 35.); so muß die Directionslinie der schweren Körper aus dem Mittelpuncte der Schwere auf die scheinbare Horizontallinie perpendicular gezogen werden.
43. Ob ein schwerer Körper in einer gegebenen Lage vor dem Falle sicher sey, oder nicht, zu finden.
1. Suchet den Mittelpunct der Schwere (§. 37.).
2. Fället aus ihm auf die scheinbare Horizontallinie ein Perpendicul (§. 69. Geom.).
[204] Wenn es innerhalb den Grund des Körpers fället; so ist er vor dem Falle sicher; fället es aber ausserhalb seinen Grund, so muß er auf die Seite fallen. W. Z. E.
Weil der Perpendicul aus dem Mittelpuncte der Schwere auf die scheinbare Horizontallinie gezogen worden; so ist er die Directions-Linie des Körpers (§. 42). Wenn aber diese innerhalb den Grund des Körpers fället, so ist er vor dem Falle sicher: fället sie aber ausserhalb den Grund, so muß er auf dieselbe Seite fallen (§. 38.). W. Z. E.
44. Durch diese Aufgabe kan man die Ursache aller möglichen Posituren finden, und den Gang der Menschen und Thiere erklären, wie Borellus in seinem Werke de motu animalium part. 1. prop. 145. & seqq. gethan.

45. Wenn an den beiden Enden A und C eines Hebels ABC zwey Gewichte G und F angehänget werden, die sich gegen einander verhalten wie die Entfernung des kleinen F zu der Entfernung des grossen G; so müssen sie einander die Wage halten, und keines kan das andere bewegen.[Fig.12]
Es sey zum Exempel F 1 Pf. und G 3 Pf. Es seyn ferner die Directionslinien der beiden Gewichte CF und AG in C und A auf AC perpendicular: so ist BC die Entfernung des Gewichtes F und [205] AB die Entfernung des Gewichtes G (§. 24.), folgends nach unserer Bedingung AB:CD = 1:3.
Weil die Schwere der Körper unverändert bleibet, wenn gleich ihre Figur verändert wird; so bilde man sich ein, daß beide Gewichte in Cylinder von gleicher Dicke verwandelt werden, und zwar dergestalt, daß ein halbpfündiges Stücke die Länge der kleinen Entfernung AB bekommet: so hält der Cylinder IK, in welchen das kleine Gewichte F verwandelt worden, 2; der andere aber HI, der aus dem grossen G entstanden, 6 solcher Theile, als AB ist. Wenn ihr euch demnach ferner einbildet, daß die Linie BC in D verlängert wird, bis CD = AB, und hingegen AB in E, bis AE =BC; so ist die Linie ED der Länge des ganzen Cylinders HK gleich. Es ist aber die Linie ED in dem Puncte B in zwey gleiche Theile getheilet, weil von B bis E 4, von B bis D auch 4 solcher Theile sind, als AB ist. Da nun der Cylinder HK seinen Mittelpunct der Schwere in dem Mittelpuncte der Grösse hat (§. 36.); so gehet die Linie BM, nach welcher er aufgehänget wird, durch den Mittelpunct seiner Schwere, folgends hänget er stille (§. 33.); und kan demnach keiner von den beiden Cylindern HI und IK, folgends auch keines von den gleichgültigen Gewichten G und F das andere überwiegen. W. Z. E.
46. Wenn derowegen die Gewichte F und G einander gleich seyn sollen; so müssen auch die Entfernungen AB und BC einander gleich seyn. Denn [206] F:G = AB:BC. Derowegen, wenn F = G, so ist auch AB = BC (§. 53. Arithm.).
47. Aus diesem einigen Lehrsatze beruhet alles, was in der ganzen Mechanick allhie zu erweisen ist. Daher wird erfordert, daß man sich denselben wohl bekannt mache. Und zu dem Ende will ich noch nach dem Exempel des Jungenickels in seinem Schlüssel zur Mechanica p. 107.108. zeigen, wie man ihn durch eine Erfahrung bestätigen kan.
48. Das Mechanische Fundamentalgesetze, oder den vorhergehenden Lehrsatz, zu probiren.[Fig.13]

1. Lasset euch den Tischer einen viereckigten prismatischen Stab abstossen, der viel breiter als dicker seyn kan, und von demselben 8 Stücke von gleicher Länge, über diese noch eines von doppelter, eines von dreyfacher und eines von vierfacher Länge abschneiden.
2. Leget den Theil von doppelter Länge auf die Schärfe eines dreyeckigten Prismatis; so werdet ihr finden, daß es darauf wagerecht liegen bleibet, wenn die beiden Theile AC und CD einander gleich sind.
3. Leget auf eben dieses Prisma das Stücke von dreyfacher Länge DE dergestalt, daß EF einen Theil und FD zwey derselben bekommet; so werdet ihr noch drey einfache Theile auf EF legen müssen, ehe DE in wagerechten Stand gesetzt wird.
4. Gleichergestalt leget auf die Schärfe des Prismatis das Stücke GH von vierfacher Länge, und [207] zwar so, daß GI drey Theile, IH einen hat; so werdet ihr noch 8 andere auf HI legen müssen, bis GH in wagerechten Stande erhalten wird.
Ich sage, dieses ist dem Fundamentalgesetze, welches in dem vorhergehenden Lehrsatze erwiesen worden, gemäß.
Denn ihr könnet setzen, die Stücke Holz hätten alle gar keine Schwere, und hienge an deren statt in ihrer Schwere Mittelpuncte, welches beiderseits in die Mitte fället (§. 36.), ein Gewichte, so ihr gleich ist (§. 35.). Weil nun im wagerechten Stande AB, DE und GH horizontal sind, und also die Directionslinien der Gewichte, so man in ihrer Mitten sich einbildet, auf den Linien AB, DE und GH perpendicular stehen (§. 41.); so sind ihre Entfernungen von den Ruhepuncten der halben Linien AC und CB, DF und FE, GI und IH gleich. Da nun die Schwere der Theile, die einander die Wage halten, sich vermöge des Versuchs gegen einander verhalten, wie ihre Entfernungen verkehrt genommen, daß, wenn z. E. IG 3 Pf. ist, und HI mit den darauf liegenden Theilen 9 Pf. hält, HI 1 und IG 3 ist; so ist klar, daß dadurch der vorhergehende Lehrsatz bestätiget wird. W. Z. E.
49. Eine Wage wird genennet ein Instrument, dadurch man die Schwere eines Körpers finden kan.

50. Eine richtige Wage zu machen.[Fig.14]
[208]1. Theilet den Wagebalken AB in zwey gleiche Theile in C, und machet nicht allein die beiden Armen AC und CB, sondern auch die Wageschalen D und E von gleicher Schwere.
2. Richtet in C das Zünglein CK perpendicular auf, und machet den Wage-Balke AB innerhalb HI beweglich.
Wenn das Zünglein inne stehet; so sind die Körper in der Wageschale von gleicher Schwere.
Wenn man die Wage in I aufhänget; so stehet HI auf der Horizontallinie perpendicular (§. 41.). Derowegen wenn das Zünglein CK innerhalb HI stehet; so ist der Wagebalken AB horizontal, weil das Zünglein auf ihm perpendicular aufgerichtet worden. Da nun die Directionslinien der Gewichte in D und E gleichfalls mit den Armen AC und CB einen rechten Winkel machen (§. 41.); so sind ihre Entfernungen den Armen AC und CB gleich (§. 24.). Weil nun AC = BC; so sind auch die beiden Gewichte in D und E einander gleich (§. 46.). W. Z. E.
51. Dannenhero ist die Wage falsch, wenn die beiden Armen AC und CB ungleich sind.
52. Eine Wage zu probiren, ob sie richtig oder falsch sey.
Verwechselt die Wageschalen oder die Gewichte, [209] welche sie in dem wagerechten Stande erhalten. Denn so er bey geschehener Verwechselung aufgehoben wird, so ist die Wage falsch: bleibet er aber, so ist sie richtig.
Wenn die Wage falsch ist; so sind die Arme ungleich (§. 51.), und dahero ist die Wageschale an dem kleinen Arme schwerer, als die an dem grossen (§. 45.). Wenn ihr nun die schwere Wageschale an den langen Arm, und die leichtere an den kurzen hänget; so muß der wagerechte Stand gehoben werden. W. Z. E.
53. Eine Schnellwage wird genennet, durch die man mit einem Gewichte Körper von verschiedener Schwere abwiegen kan.
54. Eine Schnellwage zu machen.

1. Theilet den Balken MN in so viel gleiche Theile, als euch beliebet.
2. An dem Ende des ersten Theils O richtet das Zünglein OP perpendicular auf mit seinem Behältnisse, wie in der andern Wage (§. 50.).
3. Machet den kleinen Arm OM so schwer, daß er den grossen ON in wagerechtem Stande erhält.
4. An den grossen Arm hänget ein Gewichte R, welches sich nach Belieben hin und wieder verschieben lässet. So ist die Schnellwage fertig.[Fig.15]
Weil die beiden Aerme MO und NO einander [210] im wagerechten Stande erhalten; so ist es eben so viel, als wenn sie keine Schwere hätten. Derowegen hält das Gewichte R in 1 mit einem, in 2 mit zwey, in 3 mit drey, in 4 mit vier usw. Pfunden in M die Wage (§. 45.). Und daher kan man mit einem Gewichte Körper von verschiedener Schwere abwiegen; also ist MON eine Schnellwage (§. 53.). W. Z. E.
55. Es ist sicherer, daß ihr die Puncte 1, 2, 3, 4, u. s. w. in dem langen Arme ON durch die Erfahrung determiniret, und ist alsdenn auch nicht nöthig, daß der kleine Arm vor sich mit dem langen NO im wagerechten Stande stehet, absonderlich wenn die Wagen grosse Lasten, als z. E. ein Fuder Heu, zu wiegen gebrauchet werden. Denn wenn der lange Arm schwerer ist als der kleine; so kan man mit einem kleinen Gewichte eine desto grössere Last wiegen.

56. Aus der gegebenen Schwere des Hebels AB, der Entfernung des Schwerpunctes CV, der Last CA und der Kraft CB, und der Schwere der Last, die Grösse der todten Kraft zu finden.[Fig. 1]
1. Bildet euch ein, der Hebel habe keine Schwere, und an deren statt hange in seinem Schwerpuncte V ein Gewichte G, so jener gleich ist (§. 35.); so könnet ihr die Last finden, welche ihr in A anhängen müsset, damit der Hebel wagerecht liegen bleibe (§. 45.).
2. Die gefundene Last ziehet von der gegebenen Last ab; so bleibet die Last übrig, welche die Kraft B erhalten muß.
[211] 3. Weil nun dieselbe sich zu der todten Kraft in B verhält wie BG zu CA (§. 45.); so könnet ihr diese durch die Regel Detri finden (§. 85. Arith.). W. Z. F. und Z. E.
Es sey CA = 1, CV = 2, CB = 5, G = 10 Pf., O = 300 Pf.
1–2–10 5–1–280 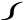
56 Pf. 10 5)25 
Kraft. 20 Pf. 30 300 Last. 30 280 0
57. Aus der gegebenen Schwere des Hebels AB, der Entfernung des Schwerpunctes CV, der Last CA und der Kraft CB, und der todten Kraft, die Schwere der Last zu finden.[Fig. 1]
1. Suchet wie in der vorhergehenden Aufgabe den Theil der Last, welchen der Hebel durch seine Schwere erhalten kan.
2. Suchet ferner auf eben dieser Art den andern Theil der Last, den die in B applicierte Kraft erhalten kan.
3. Addiret beide Theile: so kommet die Schwere der gesuchten Last heraus.
Es sey CA = 1, CV = 2, CB = 5, G = 10 Pf., die todte Kraft 56 Pf.
[212]
1–2–10 10 20 erster Theil der Last.
1––5–56 5 280 anderer Theil der Last. 20 erster Theil der Last. 300 ganze Last.
58. Aus der gegebenen Schwere der Last O und des Hebels G, der todten Kraft und der Länge des Hebels AB nebst dem Schwerpuncte des Hebels V, den gemeinen Schwerpunct C zu finden, wo nemlich der Hebel aufzulegen ist, damit die Kraft die Last erhalten kan.[Fig.1]
1. Suchet erstlich den gemeinen Schwerpunct Z der todten Kraft in B und der Schwere des Hebels G, indem ihr schliesset: wie die Summe der todten Kraft zu der Schwere des Hebels, so verhält sich VB zu ZB, oder der Entfernung der Kraft von dem gemeinen Schwerpuncte (§. 45.).
2. Ziehet ZB von AB ab, so wisset ihr AZ.
3. Bildet euch ein, es hange in Z ein Gewichte, welches der todten Kraft in B und der Schwere des Hebels G zusammen gleich ist (§. 35.); so könnet ihr wie vorhin die Linie CZ finden, folgends den Punct C, den man suchte.
[213]Es sey die Kraft in B = 56, die Schwere des Hebels G = 10, die Last O = 300 Pf. AB = 6, VB = 3.
66–10–3 3 –––30 
3066 
| 366–66– | ||
| das ist | 6111 | (§. 59. 96. Arithm.) |
| 11 | ||
| 1 = AC. | ||

59. Wenn die Last in B zwischen dem Ruhepunct C und dem Orte der Kraft in A appliciret ist; so verhält sich gleichfalls die todte Kraft in A zu der Last in B, wie die Entfernung der Last zu der Entfernung der Kraft CA.[Fig. 16]
Man verlängere CA in D bis DC = CA: so ist klar, daß die Kraft in A eben so viel vermag, als die Kraft in D (§. 46.). Wenn aber die Kraft in D das Gewichte in B erhält; so verhält sie sich zu demselben wie BC zu CD oder CA (§. 45.). Derowegen muß sich auch die Kraft in A zu der Last in B verhalten, wie BC zu CA. W. Z. E.
[214]60. Diesen Hebel wollen wir hinfüro den Hebel von der anderen Art nennen. Im Lateinischen heisset man ihn Vectem homodromum, und den ersten Vectem heterodromum.
61. Aus der gegebenen Schwere eines Hebels von der andern Art E, der Last G, dem Schwer-Puncte F, der Entfernung der todten Kraft CA, die Grösse der todten Kraft in A zu finden.[Fig. 16]
1. Suchet wie viel Kraft in A erfordert werde, den Hebel allein zu erhalten (§. 59.).
2. Suchet ferner, wie viel Kraft in A erfordert werde, die Last G allein zu erhalten (§. 59.).
3. Addiret die beiden einzelen Kräfte; so kommet die Grösse der verlangten Kraft heraus.
Es sey CB = 1, CF = 3, CA = 6, G = 300 Pf. E = 10 Pf.
| 6–3–10 | ||
| oder | 2110 | (§. 59. 96. Arithm.) |
| 1 | ||
| 5 Pf. erster Theil der Kraft. | ||
6–1–300 1 55 Pf. ganze Kraft.
62. Wenn ihr euch diese Aufgaben von dem Hebel, die bisher erkläret worden, wohl bekannt machet, und dabey dessen besinnet, was oben (§. 10.) erinnert worden; so werdet ihr das ganze Werk des Borelli de motu animalium verstehen. Unzählig viel andere Fälle will ich jetzt mit Stillschweigen übergehen, da diese Rechnungen in der Kunst, und keine Bewegung eines Körpers in der Natur, wobey man nicht dieselben anbringen könte.
63. Wenn die Kraft den Hebel aus L in M niederdrücket; so verhält sich der Raum, den die Kraft durchläuft, zu dem Raume, durch welchen die Last beweget wird, wie die Last zu der todten Kraft.[Fig. 17 und Fig.18]
Denn wenn die Kraft sich durch den Bogen LM beweget, so wird die Last durch den Bogen HN gehoben. Demnach verhält sich der Raum der Last zu dem Raume der Kraft, wie der Bogen HN zu dem Bogen LM, das ist, weil die Winkel bey I einander gleich sind (§. 40. Geom.), wie HI zu IL, folgends wie die todte Kraft zu der Last (§. 45.). W. Z. E.
64. Wenn man aus N auf HI das Perpendicul NO, und auf IL aus M das Perpendicul MR fallen lässet; so verhält sich NI zu NO wie MI zu RM (§. 10. Trigon.), folgends NI:MI = NO:RM (§.83. Arithm.). Derowegen verhält sich die Höhe, wodurch sich die Last beweget, zu der Höhe, durch welche die Kraft herunter steiget, wie die todte Kraft zu der Last.[Fig. 17 und Fig.18]
[216]65. Und daher wird so viel Kraft erfordert, 3 Pfund durch 1 Schuh, als 1 Pfund durch 3 Schuh in gleicher Zeit zu bewegen.
66. Weil man die Geschwindigkeit der Bewegung aus dem Raume beurtheilet, der in einer Zeit durchlaufen wird; so verhält sich auch die Geschwindigkeit, mit welcher sich die Kraft beweget, zu der Geschwindigkeit, mit welcher die Last beweget wird, wie die Last in der todten Kraft.
67. Man siehet demnach, daß der Hebel die Kraft nicht vermögender macht, als sie an sich ist, sondern nur in den Stand setzet, daß sie langsamer eine Bewegung hervorbringet, als sonst geschehen würde. Wenn man demnach eine Bewegung beschleunigen will; so muß man die Kraft in H und die Last in I bringen, und alsdenn ist die Kraft grösser als die Last: der Vortheil aber wird in der Zeit gesucht.[Fig.18]

68. Wenn die Directionslinie der todten Kraft mit dem Radio des Rades AC und die Directionslinie der Kraft E mit dem Radio der Welle CB einen rechten Winkel machet; so verhält sich die todte Kraft zu der Last wie der Radius der Welle CB zu dem Radio des Rades AC.[Fig. 2]
Die Kraft würde die Last erhalten, wenn gleich nur die Linie AB zurück bliebe. Da nun in C der [217] Ruhepunct ist, in B die Last, und in A die todte Kraft rechtwinklicht appliciret wird; so verhält sich diese zu jener, wie CB zu CA (§. 10. 45.). W. Z. E.
69. Wenn die Directionslinie der todten Kraft FH mit dem Radio des Rades FC einen schiefen Winkel machet; so ist es eben so viel, als wäre sie in G appliciret. Und dannenhero verhält sie sich zu der Last, wie CB zu CG.
70. Wenn euch der Winkel GFC, den die Kraft mit dem Radio des Rades machet, und der Radius des Rades gegeben sind; so könnet ihr die Linie GC durch die Trigonometrie finden (§. 20. Trigon.).
71. Es vermag die Kraft am meisten, wenn ihre Directionslinie mit dem Radio des Rades einen rechten Winkel machet (§. 25. 45).
72. Weil man sich aber bey der todten Kraft das Rad nicht anders als einen Hebel vorstellen darf (§. 10.); so lassen sich alle Aufgaben von dem Hebel auf das Räderwerk appliciren.

73. Aus der gegebenen Last C und denen Radiis der Axen BH, AD, EF, und der Räder BA, DE, FG die todte Kraft zu finden, welche in G appliciret werden muß.[Fig.19]
1. Suchet zuerst die Kraft, welche an der Peripherie [218] des ersten Rades appliciret werden müste, damit sie das an seiner Welle BH hangende Gewichte C erhalten kan (§. 68.).
2. Diese Kraft sehet als ein Gewichte an, welches an die Welle des andern Rades appliciret worden, und suchet daraus abermals (§. 68.) die Kraft, welche an der Peripherie desselben Rades appliciret werden muß, damit sie solches, folgends auch das Rad A mit seinem Gewichte C aufhalten kan.
3. Mit dieser Arbeit fahret fort, bis ihr auf die Kraft kommet, welche an der äussersten Peripherie appliciret werden muß.
Es sey C = 6000 Pf., BH = 6, AB = 34, AD = 5, DE = 35, EF = 4, FG = 27.
| 34–6–6000 | ||||
| oder | 1733 | |||
| 18000 | ||||
| 1058 oder | ||||
| 1059 Kraft in A | ||||
35–5–1059 2 
151 Kraft in E 71 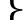

1 27–4–151 4 1 
22 Kraft in G. 605 


74. Wenn die Last gesuchet und die Kraft gegeben würde; so darf man nur von der Kraft in G anfangen, und das Gewichte in E für die Kraft in E annehmen, u. s. w.

75. Wenn eine Kraft eine Last durch Hülfe eines Rades an einer Axe beweget; so verhält sich der Raum der Kraft zu dem Raume der Last, wie die Last zu der todten Kraft.[Fig. 2]
Wenn das Rad einmal herumgedrehet wird, so gehet auch die Welle IBK einmal herum (§. 12.); und also wird die Last E so viel Schuhe herauf gehoben, als die Peripherie der Welle beträget. Derowegen stellet die Peripherie der Welle den Raum der Last, und die Peripherie des Rades den Raum der Kraft vor. Und demnach verhält sich jener zu diesem, wie die Peripherie der Welle zu der Peripherie des Rades, oder (welches gleich viel ist) wie der Radius der Welle CB zu dem Radio des Rades CA, folgends wie die todte Kraft zu der Last (§. 68.). W. Z. E.
76. Wenn viel Räder in einander gehen, so ist zu merken, daß diejenigen, so an einer Welle feste sind, in gleicher Zeit herum kommen: hingegen das kleinere, welches in das grössere greiffet, oder von dem grössern herum getrieben wird, so vielmal herum gehe, indem das grosse einmal herum kommet, wie vielmal die Peripherie des kleinen in der Peripherie des grossen, oder, welches gleich viel ist, die Zahl der Kammen im kleinen in der Zahl der Kammen im grossen enthalten ist.
[220]77. Aus den gegebenen Verhältnissen der Radiorum oder Peripherien der kleinen Räder zu den Radiis oder Peripherien der grossen, zu finden, wie vielmal dasjenige, so am geschwindesten gehet, herumkommet, ehe das, so am langsamsten beweget wird, seinen Lauf einmal vollendet.
1. Dividiret die Peripherien der grossen Räder durch die Peripherien der kleinen.
2. Die herauskommende Quotienten multipliciret in einander.

So ist das Product die Zahl, welche andeutet, wie vielmal das geschwindeste Rad G herumgehet, indem das langsamste A einmal seinen Lauf vollendet (§. 76.)[Fig. 19] W. Z. E.
Es sey die Peripherie des grossen Rades A 24, des kleinen D 12; des andern grossen Rades E 36, des andern kleinen F 9.
Also gehet das letzte Rad G 8mal herum, indem das unterste A einmal herum kommet.
78. Die Peripherien werden auch durch die Zahlen der Kammen gegeben, weil die Kammen in Rädern, die in einander greiffen, von gleicher Grösse sind.
[221]79. Die Zahl der Räder und die Zahl der Kammen an den Rädern und den Getrieben oder den Trillingsstöcken zu finden, wenn angegeben wird, wie vielmal das Rad, so am geschwindesten gehet, herumkommen soll, ehe das langsamste einmal seinen Lauf vollendet.
1. Zerfället die gegebene Zahl in andere kleine Zahlen, durch deren Multiplication sie erwächset: so sehet ihr, wie viel Räder mit Kammen und Getriebe oder Trillinge euch nöthig sind, nemlich so viel, als dergleichen Zahlen herauskommen.
2. Gebet den Getrieben nach Beschaffenheit der Umstände eine gehörige Zahl der Kammen, und multipliciret dadurch die hervor gefundenen Zahlen, so sind die Producte die Zahlen der Kammen in den Rädern, welche in die Getriebe oder Trillinge eingreifen (§. 77. 78.).
Es soll das geschwindeste Rad 40mal herum gehen, ehe das langsamste einmal seinen Lauf vollendet. Weil nun 40 durch Multiplication 5 in 8 entstehet; so sehet ihr, daß zwey Räder mit Kammen und zwey Getriebe oder Trillinge vonnöthen sind. Gebet jedem Trillinge 6 Stöcke, so bekommet das langsameste Rad A 48, das mittlere E 30, das letzte G keine Kammen, sondern dieses wird nach der Bequemlichkeit der bewegenden Kraft eingerichtet.[Fig. 19]
[222]80. Aus der gegebenen Kraft und Last die Zahl der Räder und Verhältnisse ihrer Radiorum gegen die Radios ihrer Axen, oder der kleineren an einer Welle mit ihnen befestigten Räder, zu finden.
1. Dividiret die Last durch die Kraft, so findet ihr, wie vielmal diese in jener enthalten ist.
2. Zerfället den Quotienten in verschiedene kleine Zahlen, durch deren Multiplication er entstehet. Denn soviel habt ihr Räder nöthig, als dergleichen Zahlen herauskomen, und die Diametri der Axen oder Getriebe und Trillinge verhalten sich gegen die Diametros der Räder, die mit ihnen an einer Axe befestiget sind, wie 1 zu denselben Zahlen (§. 73.). W. Z. E.
Es sey die Last 30000 Pf. die Kraft 60 Pf. so ist der Quotiet 500 Pf. Weil nun die Zahl sich in 4 • 5 • 5 • 5 zerfällen lässet, so kan man 4 Räder machen. In dreyen verhält sich der Diameter der Axe zu ihrem Diametro, wie 1 zu 5, im vierten, wie 1 zu 4.
81. Die Zerfällung der Zahlen beruhet auf der Übung. Man kan sie aber am bequemsten verrichten, wenn an die Zahl welche zerfället werden soll, durch kleine Zahlen zu dividiren suchet. Unterweilen gehet es nicht an, daß eine gegebene Zahl in lauter ganze zerfället werden kan. Derowegen muß man in diesem Falle entweder zuletzt einen Bruch beybehalten, oder wenn es die Sache leidet, die Zahl um etwas vermehren, bis sie sich bequem zerfällen lässet.
[223]
82. Wenn eine Kraft eine Last auf einer schiefliegenden Fläche AC erhält, dergestalt, daß ihre Directionslinie DK mit ihrer Länge AC parallel ist, so verhält sie sich zu der Last wie die Höhe AB zu der Länge AC.[Fig. 7]
Es sey die Directionslinie des Gewichtes DH; so kan man sich einbilden, es sey die ganze Schwere der Last in einem Puncte derselben, z. E. in F beysammen (§. 23. 35). Und demnach ist ihre Entfernung von dem Ruhepuncte EF, hingegen die Entfernung der Kraft ist die Perpendicularlinie ED (§. 24.). Da nun DEF einen Hebel vorstellet (§. 10.), dessen Ruhepunct in E; so verhält sich die Kraft in D zu der Last in F, wie EF zu ED (§. 45.). Weil nun DEG ein rechter Winkel ist, und EFG gleichfalls; hingegen der Winkel EGF den beiden Triangeln EFG und DEG gemein ist; so muß auch der Winkel EDF dem Winkel EFG, folgends der Winkel DEF dem Winkel EGF gleich seyn (§. 78. Geom.), und demnach EF:ED = GF:EG (§. 148. Geom.). Wiederum weil die Verticalwinkel bey G einander gleich (§. 40. Geom.), und bey F und H rechte Winkel sind; so ist auch GF:EG = GH:GC (§. 148. Geom.). Endlich ist auch GH:GC = AB:AC (§. 149. Geom.), und demnach EF:ED = AB:AC (§. 57. Arithm.); folgends wie AB zu AC, so die todte Kraft zu der Last. W. Z. E.
[224]
83. Wenn eine Kraft eine Last auf einer schiefliegenden Fläche LN dergestalt erhält, daß ihre Directionslinie RI mit der Grundlinie MN parallel ist; so verhält sie sich zu der Last, wie die Höhe LM zu der Grundlinie MN. [Fig. 20]
Es ist aus dem Beweise des vorhergehenden Lehrsatzes (§. 82.) klar, daß man annehmen könne, als sey in dem Hebel TQS in T die Kraft, in S die Last appliciret: folgends ist die Kraft zu der Last wie QS zu TQ oder RS (§. 45.). Da nun in dem angeführten Beweise ferner dargethan worden, daß die Triangel RQS, SQO, OPN und LNM einander ähnlich sind, so ist QS:RS = SO:QS = OP:PN = LM:NM (§. 148. 149. Geom.). Demnach verhält sich die Kraft zu der Last, wie LM zu MN. W. Z. E.
84. Weil die Schraube nichts anders ist, als eine um eine Welle herumgeführte schiefliegende Fläche (§. 20.), und die Kraft sich mit der Grundlinie parallel beweget; so verhält sich die todte Kraft zu der Last oder dem Widerstande, den sie zu überwinden hat (§. 3.), wie die Weite der Schraubengänge zu der Peripherie der Schraube.
85. Daher haben die Schrauben mit engen Gängen mehr Vermögen, als die mit weiten, wenn sie von gleicher Dicke sind.
[225]86. Wenn die Last von N bis O beweget worden; so hat man sie um OP erhoben, hingegen die Kraft hat sich durch die Linie PN beweget. Derowegen verhält sich der Raum der Kraft zu dem Raume der Last, wie die Last zu der todten Kraft. (§. 83.).[Fig. 20]
87. Eben dieses gilt auch von der Schraube. Denn wenn die Kraft sich durch die Peripherie der Schraube beweget, so wird die Last um die Weite der Schraubengänge niedergedrückt. Darum verhält sich der Raum der Last zu dem Raume der Kraft, wie die Weite zwischen zwey Gängen zu der Peripherie der Schraube, das ist, wie die todte Kraft zu der Last (§. 84.).
88. Aus der gegebenen Kraft, der Peripherie der Schraube, und der Weite der Schraubengänge, den Widerstand zu finden, den die Kraft mit einer Schraube überwinden kan.
Suchet zu der Weite zwischen den Schraubengängen, der Peripherie der Schraube und der Kraft die vierte Proportionalzahl (§. 85. Arithm.) so ist geschehen, was man verlangete.
Es sey die Weite der Schraubengänge 3", die Peripherie der Schraube 25", die Kraft 30 Pf. [226]
3–25–30 (§. 95. Arithm.). 11010 250 Last.
89. Aus der gegebenen Kraft und Last die Eintheilung der Schraube zu finden.
1. Dividiret die Last durch die Kraft; so ist 1 die Weite der Schraubengänge und der Quotient die Peripherie der Schraube (§. 84.).
2. Nehmet nach Erforderung der Umstände die Weite der Schraubengänge in Zollen oder Linien an, und multipliciret dadurch den vorherigen Quotienten; so habet ihr die Peripherie der Spindel in Zollen oder Linien (§. 85. Arithm.) und
3. könnet daraus ihren Diameter (§. 133. Geom.) finden.
Es sey die Last 250 Pf. die Kraft 30 Pf.
1 

8 Weite der Gänge 
3’’’ 25 Peripherie der Spindel.
31–4100–25 100 2500
30 
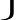
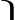
7 oder 7 Diameter der Spindel. 

90. Wenn ihr demnach die gefundene Peripherie der Spindel 25’’’ auf die Linie BC traget, und in B ein Perpendicul aufrichtet (§. 70. Geom.), darauf die Weite der Gänge AB aus B gegen A so vielmahl traget, als Gänge werden sollen, und das Rectangulum ADCB construiret (§. 99. Geom.); so könnet ihr die Gänge B 1, 1.2, 2.3, 3.4. u. s. w. ziehen. Wenn ihr nun diesen Riß um die Spindel klebet; so ist die Eintheilung der Schraube richtig. [Fig. 21]
91. Man beweget öfters die Schrauben durch einen Ziehstengel, welcher mit der Spindel ein Rad an einer Axe formiret (§. 13.), und dannenhero die Kraft noch über das Vermögen der Schraube vermehret (§. 68.)

92. Wenn die Schraube in ein Stirnrad eingreiffet, so nennet man sie die Schraube ohne Ende. [Fig. 22]
93. Die Kammen in dem Stirnrade müssen nach den Schraubengängen eingeschnitten werden, das ist, nach dem Winkel der Spindel.
94. Die Schraube ohne Ende darf nicht mehr als drey Gänge haben.
95. Wenn die Schraube einmal herumgedrehet wird; so windet sich in dem Stirnrade ein Kammen aus, und ist demnach die Bewegung sehr langsam.
[228]
96. Wenn die Kraft D mit einem um eine Rolle C gezogenen Seile eine Last E erhält; so ist sie der Last gleich. [Fig. 6]
Die Kraft D verhält sich zu der Last E, wie BC zu CA (§. 18 45.). Nun ist AC = CB (§. 18.). Derowegen ist die Last der Kraft gleich (§. 53. Ar.). W. Z. E.

97. Wenn die Kraft E eine Last F mit einem um eine Rolle gezogenen Stricke dergestalt erhält, daß die beiden Stricke parallel sind, und die Rolle zugleich mit der Last hinauf gezogen würde, wenn eine Bewegung geschähe, so verhält sich dieselbe zur Last, wie 1 zu 2. [Fig. 23]
Weil der Strick in D feste ist, und das Gewichte F in H hänget; so verhält sich die Kraft zu demselben, wie AH zu AB (§. 59.). Nun ist AH = AB (§. 18.). Derowegen ist auch die Kraft die Hälfte der Last. W. Z. E.
98. Daher vermehren in einem Kloben nicht die oberen, sondern nur allein die unteren Scheiben das Vermögen.

99. Wenn in einem Kloben alle Stricke MN, SX, QR, PO, TV, einander parallel sind; so verhält sich die Kraft in Z zu der Last W, [229] wie 1 zu der Zahl der Seile, die von der Last gezogen werden. [Fig. 24]
Denn weil in diese Falle alle Stricke gleich gedehnet werden; so wird die ganze Last durch dieselbe vertheilet. Dannenhero hat die Kraft in Z nicht mehr zu erhalten, als was auf den Strick N kommet (§. 96.). Solchergestalt verhält sich die Kraft zu der Last, wie 1 zu der Zahl der Stricke, die von der Last gezogen werden. W. Z. E.
100. Wenn ihr durch die Zahl dieser Stricke (5) die Last (500) dividiret; so kommet die Kraft (100) heraus.
101. Hingegen wenn ihr die Kraft (100) durch die Zahl der Stricke (5) multipliciret; so kommet die Last (500) heraus.
102. Und weil die Zahl der oberen und unteren Rollen zusammen in einem Kloben der Zahl der Seile gleich sind; so kommet selbige heraus, wenn ihr die Last (500) durch die Kraft (100) dividiret.
103. Zuweilen setzet man die Scheiben in dem Kloben nicht über, sondern neben einander, absonderlich wenn ihrer viel sind, damit man den Raum ersparet.
104. Wenn eine Last durch einen Kloben beweget wird; so verhält sich der Raum der Kraft zu dem Raume der Last, wie die Last zu der todten Kraft.
[230]Wenn das Gewichte oder die Last um einen Schuh erhöhet werden soll; müssen alle Stricke, die von ihr gedehnet werden, um einen Schuh verkürzet werden. Also muß die Kraft so viel Schuhe herausziehen, als Seile sind. Darum verhält sich ihr Raum zu dem Raume der Last, wie 1 zu der Zahl der Stricke, die von der Last gedehnet werden, das ist, wie die todte Kraft zu der Last (§. 99.). W. Z. E.

105. Bey einem Keile verhält sich die Kraft zu der Last oder dem Widerstande, den die Sache, so zerspaltet werden soll, auf der Seite LN giebet, wie die halbe Dicke ML zu der Länge MN. [Fig. 20]
Der Keil ist aus zwey schiefliegenden Flächen zusammengesetzet. Da es nun gleichviel ist, ob man die Last auf derselben beweget, oder ob man diese mit Gewalt darunter wegstösset, und die Directionslinie der Kraft, die mit einem Keile spaltet, mit der Länge eines Keiles übereinkommt; so verhält sich die Kraft zu der Last auf der Seite LN wie die halbe Dicke ML zu der Länge MN (§. 83.). W. Z. E.
106. Derowegen vermag ein spitziger Keil mehr, als ein stumpfer, weil ML zu MN in jenem eine kleinere Verhältniß, als in diesem hat.
[231]107. Wenn das Wasser, welches eine[WS 1] Maschine treibet, von oben auf das Rad fället und auf ihm liegen bleibet, damit es durch seine Schwere auf der einen Seite das Rad ferner niederdrücket; so nennet man es ein oberschlächtiges Wasser-Rad.
108. Hingegen ein unterschlächtiges Wasser-Rad ist, wenn es über dem Wasser hänget, und durch seinen schnellen Schuß beweget wird.
109. Weil das Wasser selten, ausser in gar grossen Flüssen, einen schnellen Strom hat, daß es Mühlen treiben könte; so muß es durch den Fall wie andere schwere Körper lebend gemachet werden, und daher der Ort, wo das Wasser-Rad stehen soll, viel niedriger liegen, als der Ort, wo es hergeleitet wird.
110. Weil aber das Wasser sein Gefälle von einem Orte bis zum andern nach und nach bekommet; so muß man ihm solches auf einmal geben, wenn es lebend werden soll, und dannenhero wissen, wie viel man Gefälle hat, das ist, wie viel der Ort, wo das Wasser-Rad stehen soll, dem Mittelpuncte der Erde näher ist, als der andere, wo es hergeleitet ist.
111. Das Wasser-Wägen ist eine Kunst, zu [232] finden, wie viel ein Ort dem Mittelpuncte der Erde näher ist, als ein anderer.
112. Weil die Horizontallinie in allen ihren Puncten von dem Mittelpuncte der Erde gleichweit weg ist (§. 28.); so dürfet ihr nur die Horizontallinie des einen Ortes bis an den andern Ort fortziehen, und in dem letzten messen, wie viel er unter der Horizontallinie des ersten lieget.
113. Daher muß im Wasser-Wägen vor allen Dingen die Horizontallinie gefunden werden.

114. Eine Wasser-Wage zu machen, das ist, ein Instrument, damit man die Horizontallinie finden kan. [Fig. 25]
1. Schneidet aus einem wohlgehobelten Brete einen halben Circul ACDB und theilet ihn aus dem Mittelpunct C durch eine zarte Linie DH in zwey gleiche Theile.
2. Schlaget in F und E zwey Haken ein, und
3. hänget aus dem Mittelpuncte an einem zarten Faden oder Pferdehaare eine bleyerne Kugel.
Wenn ihr das Instrument mit dem Haken F und E an einer Schnure aufhänget und der Faden des Bleywurfs fället in die Linie DH; so ist sowohl die ausgespannete Schnure, als die Diameter des Instruments AB ein Theil von der scheinbaren Horizontallinie.
[233]Die Directionslinie der schweren Körper stehet auf der scheinbaren Horizontallinie perpendicular (§. 41.). Nun ist der Faden des Bleywurfes die Dirctionslinie der bleyernen Kugel (§. 23.) und fället auf die Linie AB perpendicular, wenn sie die Linie DH decket (§. 17. 37. Geom.). Derowegen muß in solchem Falle die Linie AB ein Theil der scheinbaren Horizontallinie seyn. W. Z .E.

115. Es hat schon Ricciolus (Geogr. Refor. lib. 6. c. 26. f. 129.) angemerket, daß man mit dieser Wasser-Wage in grossen Weiten leicht fehlen kan, wenn sie nicht sehr groß ist; indem sie den Unterschied von 5 Minuten, ja wol halben Graden kaum andeutet. Wenn sie aber groß ist, kan man sie nicht bequem hin und wieder tragen. Doch pfleget man in diesem Falle an statt des halben Circuls nur ein dünnes Bret EGHF an den Diameter AB rechtwinklicht anzuleimen, damit der Radius CD bis in G verlängert werden kan. Andere Arten der Wasser-Wagen mit Dioptern beschreibe ich in den Anfangs-Gründen. [Fig. 26]
116. Das Gefälle des Wassers ist eine gerade Linie, um welche die Oberfläche desselben in einem Orte dem Mittelpuncte der Erde näher ist, als an einem anderen.

117. Das Wasser zu wägen, oder sein Gefälle zu finden, mit einer Wage, so Dioptern hat. [Fig. 27]
1. Lasset an beiden Orten des Ufers, wo ihr anfanget, [234] und wo ihr aufhöret zu wägen, einen Bleywurf auf die Fläche des Wassers fallen, damit ihr die Höhe des Ufers dadurch zu wissen bekommet: die ihr in euer Memorial eintragen müsset.
2. Setzet die Wasser-Wage an das erste Ufer A, und an dem anderen Ufer B stecket einen Stab perpendicular ein, an welchem ihr eine viereckichte Tafel, die schwarz angestrichen, und nur mitten einen weissen Circul, oder auch ein weisses Creutze hat, auf und nieder nach Belieben verschieben, und durch eine Stellschraube befestigen könnet.
3. Zielet durch die Dioptern nach der Scheibe, und lasset sie so lange erhöhen, oder erniedrigen, bis ihr den Mittelpunct der Scheibe erzielet.
4. Messet von A bis in D die Höhe des Auges AD, und von B bis in C die Höhe des Mittelpunctes der Tafel C.
5. Addiret zu der ersten die Höhe des Ufers in A, zu der andern die Höhe des Ufers in B.
6. Weil ihr nun auf solche Weise wisset, wie weit die Linie DC, welche mit der Horizontallinie in A parallel laufet, an beiden Orten von der Oberfläche des Wassers weg ist; so dürfet ihr nur die erste gefundene Summe von der anderen abziehen; so bleibet das Gefälle übrig, welches ihr finden soltet. Man muß sich hier einbilden, als wenn die Wasser-Wage, so in P ist, anstatt der Tafel D, in A stünde.
[235]| Höhe des Ufers in A 64’’ | Höhe in B 58’’ |
| AD 56 | BC 72 |
| 120 | 130 |
| 120 | |
| Gefälle 10. |
7.Wenn ihr von einem Orte in den andern nicht sehen könnet, so verfahret stückweise, daß ihr nemlich die gegebene Weite in etliche Theile eintheilet. Weil ihr aber unterwegens Oerter antreffen könnet, die höher liegen als der Ort, wo ihr anfanget; so setzet die Wasser-Wage EF zwischen zwey Stäbe AQ und BH, traget die Erhöhungen des Mittelpuncts in der Tafel D zur Linken jederzeit besonders, und die Erhöhungen des Mittelpuncts der Tafel C zur Rechten gleichfalls besondes in euer Memorial. Addiret die ersten zu einander, und die andern auch zu einander; so dürfet ihr nur die beiden Summen von einander abziehen, wenn ihr das Gefälle finden wollet. [Fig. 27]
| Linke Höhe AD 4’’ | Rechte Höhe BC 57’’ |
| BO 68 | MP 102 |
| Höhe des Ufers 64 | Höhe des Ufers 58 |
| 166 | 217 |
| 166 | |
| Gefälle 51. |
Mit der vorhin beschriebenen Wage wird nur der Strick an den Stäben angezogen, und brauchet man keine Tafeln.
[236]
118. Eine Maschine durch den Wind zu bewegen.[Fig. 28]
1. Machet 4 Wind-Flügel aus Schindeln, wie die Figur zeiget. Die Länge EA ist bis 30’, die Breite HI 6’. Sie werden an der Welle FL unter einem Winkel von 45° befestigt. Denn wenn sie nach einem rechten Winkel auf die Axe gesetzet würden, könte sie der Wind nicht herumtreiben. Am besten ist es, wenn man sie unter einem Winkel von 54° auf die Axe setzet; so hat der Wind die gröste Gewalt, sie zu bewegen.
2. Weil nun die Flügel beständig dem Winde entgegen gekehret seyn müssen; so hänget die ganze Maschine beweglich an einer Spindel K dergestalt, daß sie durch einen an ihr Gehäuse befestigten Hebel PQ nach Gefallen herumbeweget werden kan.

1. Führet das Haus von Steinen auf bis unter das Dach, welches ihr nach Belieben müsset herumdrehen können.[Fig. 29]
2. Durch das Dach lasset die Welle mit den Wind-Flügeln gehen, die wie vorhin verfertiget worden.
3. Oben an das Dach befestiget einen Baum AB, der gerade heruntergehet, bis auf den Gang den ihr circulrund um das Gebäude herumgeführet.
[237] 4. Verbindet denselben noch mit einem andern AC, der oben in C gleichfalls an das Dach befestiget ist.
5. Auf dem Gange schlaget hin und wieder eiserne Hacken ein.
Wenn ihr nun das Seil DF an einen Hacken anhänget, und es mit der Winde G aufwindet; so ziehet sich das Dach mit den Wind-Flügeln gegen den Hacken herum.
119. Die erste Manier ist bey uns in Deutschland, die andere aber in Holland bräuchlich. Damit in der Holländischen das Dach sich bequem herumdrehen lässet, müsset ihr oben um das Gebäude einen hölzernen Ring machen, und in denselben einen Canal vertiefen. In den Boden des Canals setzet dergestalt messingene Rollen ein, daß sie ein wenig über denselben hervorgehen. Endlich verbindet das Dach an einen hölzernen Ring, der in den Canal gesenket werden kan.
120. Eine Maschine zu machen, die ein Thier durch Ziehen bewegen kan.
1. Richtet eine Welle auf den Horizont perpendicular auf, und
2. machet an dieselbe eine Deichsel von ohngefehr 7 bis 8 Schuhen, oder auch länger, nachdem es die Umstände erfordern, damit man ein Pferd oder einen Ochsen anspannen kan.
3. Oben an der Welle befestigt horizontal ein etwas grosses Stirnrad, und verbindet es mit der Welle durch starke Hölzer, welche an der Zahl und Länge den Armen des Rades gleichen, aber nur etwan halb so breit und noch einmal so dicke seyn können. Z. E. Es sey die [238] Länge eines Armes 17 Schuhe, die Dicke 2 Zoll, die Breite 7 Zoll, die Zahl derselben 16: so könnet ihr auch 16 Hölzer zum Verbinden nehmen und 7 Schuhe lang, 8 Zoll dicke, 7 Zoll breit machen.
So ist geschehen, was man verlangte.
121. Eine Maschine zu machen, die ein Thier durch Treten bewegen kan.
1. Machet ein grosses Rad, und setzet die Schauffeln wie in einem oberschlächtigen Wasser-Rade ein.
2. Ueber dem Rade bauet einen Stall für den Ochsen, der es treten soll, und schneidet in den Boden ein Loch, wo die Hinterfüsse des Ochsen zu stehen kommen, damit er auf die Schaufeln des Rades treten kan.
3. Weil nun das Rad auf derselben Seite sich niederdrücket; so ziehet der Ochse die Füsse zurücke und tritt auf die folgende Schaufeln. Dergestalt wird das Rad beweget.
122. Wenn ihr kleine Lasten zu bewegen habet, z. E. einen Braten an einem Spiesse; so könnet ihr anstatt der Schaufeln das Rad an der Stirne ganz mit Bretern beschlagen und einen Hund inwendig hineinsetzen, der es mit seinen Füssen herumtreibet.

123. Eine Maschine zu machen, die ein Mensch durch Drücken[WS 2] bewegen kan.[Fig. 30]
[239]Machet an eine horizontalgelegte Welle verschiedene Armen, die durch den Mittelpunct der Axe gehen, oder wenigstens gegen denselben eingesetzet sind. Denn wenn ihr mit der Hand einen Arm DC, AB nach dem andern ergreifet und niederdrücket; so wird die Welle herumbeweget. W. Z. T. W.

124. Eine Maschine durch Drehen zu bewegen.[Fig. 31]
Machet an die Welle entweder eine gerade ABCD (n. 1.), oder eine gekröpfte Kurbe (n. 2.) EFG; so könnet ihr die Welle mit herumdrehen. W. Z. T. W.
125. Eine Maschine durch Stossen zu bewegen. [Fig. 3]

Dieses geschiehet durch Hülfe der Winde FIHG.
126. Eine Maschine durch Treten zu bewegen.
Machet ein grosses Rad, darinnen zwey Kerle stehen können, fast auf eben die Art, wie in der Anmerkung der 21. Aufgabe (§. 122.) angewiesen worden.

1. Leget einen Hebel HF horizontal, dergestalt, [240] daß sein Ruhepunct in F um einen Nagel beweglich ist.[Fig. 32]
2. Hänget ihn durch Hülfe einer Stangen EH an die Kurbe EL, die in eine Welle eingeschlagen ist.
Wenn ihr mit dem Fusse auf G tretet und den Hebel niederdrücket; bald darauf den Fuß wieder in die Höhe hebet u. s. w. so werdet ihr die Welle herumtreiben. W. Z. T. W.
127. Weil in dem letzten Falle die Last, so man in H appliciret zu seyn sich gedenken muß, von dem Ruhepunct F weiter weg ist, als der Fuß, welcher auf G tritt; so muß man mehr Kraft zur Bewegung anwenden, als die Last ist (§. 59.). Und dannenhero ist diese Manier die Bewegung nur zu gebrauchen, wo man eine geringe Last zu bewegen hat. Ihr könnet aber mit Vortheil die Stange in G appliciren und mit der Hand bey H den Hebel bewegen. [Fig. 33]
128. Eine Maschine durch Gewichte zu bewegen.[Fig. 34]
1. Wickelt einen Strick um eine Welle LM, die horizontal lieget, und
2. ziehet ihn um eine Rolle G, die so hoch an einen Balken eingeschraubet, als nur immer möglich ist.
3. An das Ende des Strickes hänget das Gewichte P.
Weil dieses durch seine Schwere hinunter steiget [241] und den Strick abwickelt, so drehet es die Welle herum. W. Z. T. W.
129. Je tiefer das Gewichte zu steigen hat, je langsamer laufet der Strick ab, (als welcher in diesem Fall weit länger, als sonst seyn kan); und je länger dauret dannenhero die Bewegung.
130. Ihr könnet machen, daß der Strick langsam ablaufet, wenn ihr ihn durch einen Kloben ziehet. Denn wenn z. E. der Kloben 4 Rollen hat, so laufen von der Welle 4 Schuh Stricke ab, ehe das Gewichte P einen Schuh niedergestiegen (§. 34. 104.).[Fig. 34]

131. Die bewegende Kraft durch ein Gewichte zu verstärken.[Fig. 35]
Ihr sollet z. E. eine Last E von 100 Pf. in die Höhe ziehen.
1. Bindet die Last E an einen Strick, und
2. Ziehet ihn um die Rolle HF.
3. An das andere Ende hänget ein Gewichte D, welches etwas weniger als die Last E wieget.
Wenn ihr nun mit der Hand den Strick DH herunter ziehet; so brauchet ihr ganz wenig Kraft, die Last E in die Höhe zu ziehen.

132. Eine Maschine durch eine Feder zu bewegen.[Fig. 36]
[242]1. Lasset ein Blech aus Stahle schmieden, und wickelt es in die Runde über einander zusammen; so ist die Feder AB fertig.
2. Schliesset sie in eine Cylindrische Büchse ein, und befestiget daran das eine Ende der Kette oder Saite.
3. Weil nun die Feder, wenn sie aufgezogen ist, anfangs stark, hernach immer schwächer ziehet; so müsset ihr die Welle GLHI, darum die Saite oder Kette gewickelt ist, nicht von gleicher Dicke, sondern auf eine Conische Art machen. Denn wenn die Kraft gleich anfangs stark, gegen das Ende schwächer ist; so ist sie doch im Anfange dem Ruhepuncte E näher, als zu Ende; und also wird ihr Vermögen in dem ersten Falle vergeringert, in dem andern verstärket (§. 45.).
133. Wie viel die Welle GH von G gegen H nach und nach zunehmen soll, hat man bisher durch die Erfahrung ausgemacht, indem man durch das Gehör geurtheilet, ob die Uhren, die man durch die Federn beweget, gleich gehen, oder nicht. Allein Schottus in seiner Technica curiosa lib. 9. cap. 4. prop. 10 p. 641. erfordert mit Recht, man solle nach der Bewegung eines Perpendiculs untersuchen, ob das Rad an einer Uhr, welches sich am längsten beweget, immer in einer Zeit herumkommet.

134. Die Bewegung der Maschinen zu regulieren, daß sie einmal so geschwinde als das andere gehen.[Fig. 33]
[243]Man brauchet hierzu die Schwung-Räder MN, welche entweder an der ganzen Peripherie mit Bley ausgegossen, oder nur an vier Orten mit gleichweit von einander abstehenden Gewichten versehen werden.
An den Uhrwerken appliciret man aus gleicher Absicht einen Perpendicul.
135. Die Schwungräder sind nöthig in Maschinen, welche von Menschen und Thieren bewegt werden, damit sie nicht zuweilen in der Bewegung nachlassen.









































