Mathematische Principien der Naturlehre/Buch1-I
| ← Grundsätze oder Gesetze der Bewegung | Mathematische Principien der Naturlehre (1872) von Isaac Newton, übersetzt von Jakob Philipp Wolfers Buch I. Abschnitt I |
Buch I. Abschnitt II. → |
§. 1. Lehnsatz. Grössen, wie auch Verhältnisse von Grössen, welche in einer gegebenen Zeit sich beständig der Gleichheit nähern und einander vor dem Ende jener Zeit näher kommen können, als jede gegebene Grösse, werden endlich einander gleich.
Wollte man dies bestreiten, so sei ihr letzter Unterschied = D. Sie könnten sich daher der Gleichheit nicht weiter nähern, als bis auf den gegebenen Unterschied, was gegen die Voraussetzung ist.
§. 2. Lehnsatz. Werden in der beliebigen Figur AacE, welche durch die geraden Linien Aa, AE und die Curve acE begrenzt ist, beliebig viel Parallelogramme Ab, Bc, Cd etc. auf gleichen Grundlinien AB, BC, CD, etc. und den Seiten Bb, Cc, Dd, etc. ∥ Aa beschrieben; fügt man hierauf die Parallelogramme
hinzu; vermindert man ferner die Breite AB = BC = CD etc. dieser Parallelogramme und vermehrt man zugleich ihre Anzahl bis ins unendliche: so wird zuletzt die eingeschriebene Figur gleich der umschriebenen, gleich der krummlinigen Figur, d. h.
Der Unterschied der eingeschriebenen und umschriebenen Figur ist nämlich
weil AB = BC = CD = DE. AalB wird aber dadurch, dass man seine Breite AB bis ins Unendliche vermindert, kleiner als jede angebbare Grösse; mithin werden (nach §. 1.) die eingeschriebene und die umschriebene, und noch weit mehr die zwischen beiden liegende krummlinige Figur einander gleich. W. z. b. w.
§. 3. Lehnsatz. Die letzten Verhältnisse dieser drei Figuren werden auch dann einander gleich, wenn die Breiten AB, BC, CD etc. der Parallelogramme ungleich sind und dieselben alle bis ins Unendliche verkleinert werden.
Es sei AF die grösste Breite, und man vollende das Parallelogramm FAKf. Dasselbe wird grösser sein, als der Unterschied zwischen der eingeschriebenen und der umschriebenen Figur, und wenn man seine Breite AF in’s Unendliche vermindert, wird es selbst kleiner als jedes angebbare Rechteck. W. z. b. w.
Zusatz 1. Die letzte Summe der verschwindenden Parallelogramme fällt daher in jeder Beziehung mit der krummlinigen Figur zusammen.
Zusatz 2. Noch weit mehr fällt die geradlinige, von den zu den entsprechenden Bogen gehörigen Sehnen ab, bc, cd etc. eingeschlossene Figur zuletzt mit der krummlinigen zusammen.
Zusatz 3. Dasselbe gilt von der geradlinigen Figur, welche durch die, den Sehnen entsprechenden, Tangenten begrenzt ist.
Zusatz 4. Daher sind diese letzten Figuren, was den Umfang acE betrifft, nicht geradlinige, sondern krummlinige Grenzen gerader Linien.
| Fig. 7. | Fig. 8. |
§. 4. Lehnsatz. Wenn in zwei Figuren AacE, PprT wie vorhin zwei Reihen Parallelogramme, deren Anzahl in beiden gleich, eingeschrieben und ihre Breiten ins Unendliche vermindert werden; wenn ferner die letzten Verhältnisse der einzelnen Parallelogramme in der einen Figur zu den einzelnen in der andern dieselben sind: so stehen beide Figuren AacE und PprT zu einander in demselben Verhältniss.
Da nämlich die Summe der einzelnen Parallelogramme sich wie diese verhalten, so stehen beide Figuren in demselben Verhältniss, indem nach §. 3. die Summe der Parallelogramme in jeder Figur zu dieser selbst im Verhältniss der Gleichheit steht.
Zusatz. Theilt man daher zwei Grössen beliebiger Art in dieselbe beliebig grosse Anzahl Theile, und haben diese bei unendlicher Vermehrung ihrer Anzahl und unendlicher Verminderung ihrer Grösse, zu einander, nämlich der erste zum ersten, der zweite zum zweiten, u. s. w. f. ein gegebenes Verhältniss; so stehen die ganzen Grössen zu einander in demselben Verhältniss. Werden nämlich in den Figuren dieses Lehnsatzes die Parallelogramme untereinander als Theile betrachtet, so sind die Summen der Theile immer als Summen der Parallelogramme anzusehen. Mithin stehen diese Summen, bei unendlicher Vermehrung der Anzahl und unendlicher Verminderung der Grösse der Parallelogramme in demselben Verhältniss wie die Parallelogramme, d. h. nach der Voraussetzung, in dem letzten Verhältniss des einen Theils zum andern.
§. 5. Lehnsatz. Alle einander correspondirenden Seiten ähnlicher Figuren sind proportional, sowohl die krumm- als die gradlinigen, und ihr Flächeninhalt verhält sich wie die Quadrate der Seiten.
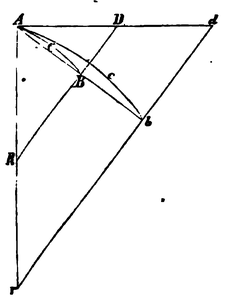
§. 6. Lehnsatz. Wird ein der Lage nach gegebener Bogen ACB durch die Sehne AB unterspannt, und in irgend einem Punkte A, in der Mitte der continuirlichen Krümmung durch die gerade Linie AD berührt; nähern sich hierauf die Punkte A und B einander und treffen sie endlich zusammen: so wird der Winkel BAD, welchen Sehne und Tangente mit einander bilden, in’s Unendliche vermindert und verschwindet zuletzt.
Verschwände der Winkel nicht, so würde der Bogen ACB mit der Tangente AD einen Winkel einschliessen, welcher einem geradlinigen gleich wäre und es würde die Krümmung im Punkte A nicht stetig sein, was gegen die Voraussetzung ist. Oder auch: Verlängert man AB bis b und AD bis d, so muss, wenn A und B zusammenfallen, und kein Theil AB von Ab mehr innerhalb der Curve liegt, die gerade Linie Ab entweder mit der Tangente Ad zusammenfallen, oder zwischen der Tangente und der Curve gezogen werden. Der letzte Fall ist gegen die Natur der Krümmung, daher findet der erstere statt. W. z. b. w.
§. 7. Lehnsatz. Bei denselben Voraussetzungen ist das letzte Verhältniss des Bogens, der Sehne und der Tangente zu einander das der Gleichheit.
Wir verlängern, während B sich A nähert, AB und AD bis nach b und d, und ziehen
und es sei stets Bogen
Fallen nun die Punkte A und B zusammen, so verschwindet nach §. 6. der Winkel dAb; folglich fallen die geraden Linien Ab, Ad und der zwischenliegende Bogen Acb zusammen und sind daher einander gleich. Daher werden auch die denselben proportionalen, geraden Linien AB, AD und der Bogen ACB, verschwinden und als letztes Verhältniss das der Gleichheit haben. W. z. b. w.
Zusatz 1. Zieht man
und schneidet BF die beliebige Linie AF in F, so hat BF zum verschwindenden Bogen AB zuletzt das Verhältniss der Gleichheit. Es ist nämlich nach Vollendung des Parallelogrammes AFBD
Zusatz 2. Werden durch B und A beliebige gerade Linien BD, BE, AF, AG gezogen, welche die Tangente AD und die ihr parallele Linie BF in den Punkten D, E, F, G schneiden; so wird das letzte Verhältniss aller Abscissen AD, AE, BF, BG, der Sehne AB und des Bogens ACB das der Gleichheit.
Zusatz 3. Daher kann bei jedem die letzten Verhältnisse betreffenden Beweise, jede dieser Linien gegenseitig statt der andern gesetzt werden.
§. 8. Lehnsatz. Bilden die gegebenen geraden Linien AB und BR mit dem Bogen ACB, der Sehne AB und der Tangente AD die Dreiecke
und nähern sich die Punkte A und B einander gegenseitig; so wird die letzte Form dieser einander ähnlich und ihr letztes Verhältniss das der Gleichheit.
Man verlängere AB, AD, AR bis b, d, r, ziehe
und
Fallen nun die Punkte A und B zusammen, so verschwindet der Winkel bAd, es fallen daher die Dreiecke
zusammen, und sind einander congruent; folglich werden auch die ihnen ähnlichen Dreiecke
einander congruent. W. z. b. w.
Zusatz. Diese Dreiecke können mithin überall, wo es sich hier um ihre letzten Verhältnisse handelt, statt einander gesetzt werden.
§. 9. Lehnsatz. Die ihrer Lage nach gegebene Curve ABC und gerade Linie AE schneiden sich im Punkte A, und zu den Abcissen AD, AE gehören die Ordinaten DB, EC. Lässt man nun die Punkte B und C dem A sich nähern, so stehen die Dreiecke ADB und AEC zuletzt im doppelten Verhältniss der Seiten.
Man nehme nämlich auf der verlängerten Linie AD die Punkte d und e dergestalt an, dass
und die zugehörigen Ordinaten
Ferner verlängere man AC bis c, und ziehe
und die Tangente Ag an beiden Curven, welche die Ordinaten in
schneidet. Fallen nun die Punkte B und C mit A zusammen, so verschwindet der Winkel cAg, und es fallen die krummlinigen Figuren
mit den geradlinigen
zusammen. Nach §. 5. werden sie sich daher verhalten, wie
Diese Flächen Abd, Ace sind aber stets proportional den Flächen ABD, ACE, und die Seiten Ad, Ae den Seiten AD, AE. Es ergiebt sich daher als letztes Verhältniss
§. 10. Lehnsatz. Die Wege, welche der Körper in Folge der Wirkung irgend einer endlichen regelmässigen Kraft beschreibt, mag diese bestimmt und unveränderlich sein, oder mag sie beständig zu- oder abnehmen, stehen beim Anfange der Bewegung im doppelten Verhältniss der Zeiten.
Werden nämlich die Zeiten durch die Linien AD, AE (vor. Figur) und die erzeugten Geschwindigkeiten durch die Ordinaten DB, EC ausgedrückt; so bezeichnen die Flächen ABD, ACE die mit diesen Geschwindigkeiten oder durch diese Ordinaten beschriebenen Wege, und dieselben stehen beim Anfange der Bewegung (nach §. 9.) im doppelten Verhältniss der Zeiten AD, AE. W. z. b. w.
Zusatz 1. Hieraus kann man leicht Folgendes schliessen: Körper beschreiben ähnliche Theile ähnlicher Figuren in proportionalen Zeiten, und erzeugen vermöge gleicher Kräfte, welche an jenen Theilen auf ähnliche Weise angebracht sind, Abweichungen vom Wege, welche von dem Orte der Figur aus gemessen werden, zu dem diese Körper ohne jene Kräfte in denselben proportionalen Zeiten gelangen würden. Es verhalten sich alsdann diese Abweichungen nahe, wie die Quadrate der Zeiten, in denen sie erzeugt werden.
Zusatz 2. Die Abweichungen aber, welche durch proportionale und ähnlich angebrachte Kräfte erzeugt werden, verhalten sich wie die Kräfte und die Quadrate der Zeiten zusammengenommen.
Zusatz 3. Dasselbe gilt von beliebigen Räumen, welche die Körper, unter der Einwirkung verschiedener Kräfte beschreiben. Diese Räume verhalten sich, im Anfange der Bewegung selbst, wie die Kräfte und die Quadrate der Zeiten zusammengenommen.
Zusatz 4. Daher verhalten sich im Anfange der Bewegung die Kräfte direct wie die beschriebenen Wege, und indirect wie die Quadrate der Zeiten.
Zusatz 5. Ferner verhalten sich die Quadrate der Zeiten direct wie die beschriebenen Wege und indirect wie die Kräfte.
§. 10a. Anmerkung. Werden unbestimmte Grössen verschiedener Art mit einander verglichen und sagt man, irgend eine von ihnen verhalte sich direct oder indirect wie eine andere, so hat man diesen Ausspruch so zu verstehen, dass die erstere in demselben Verhältniss zu- oder abnehme, wie die zweite oder deren Reciprokes. Sagt man ferner, eine von ihnen verhalte sich, wie irgend zwei oder mehrere der andern direct oder indirect; so heisst dies, erstere nehme zu oder ab in einem Verhältniss, welches aus den Verhältnissen zusammengesetzt ist, in denen die andern Grössen oder ihre Reciproke zu- oder abnehmen. Wenn also A sich verhält direct wie B, direct wie C und indirect wie D; so nimmt A zu oder ab in demselben Verhältniss wie
d. h. A und stehen zu einander im gegebenen Verhältniss.
§. 11. Lehnsatz. Die Linie AD sei eine Tangente an der Curve AbB und BD beliebig von B nach D gezogen; alsdann steht BD beim Verschwinden zuletzt im doppelten Verhältniss der zugehörigen Sehne AB.
1. Fall. Es sei BD auf AD perpendikulär, und man ziehe BG senkrecht auf AB und AG senkrecht auf AD, so dass beide Perpendikel einander in G schneiden. Hierauf mögen die Punkte D, B, G nach d, b, g rücken und es sei J der letzte Durchschnittspunkt der Linien AG und BG, wenn die Punkte D und B bis nach A gelangt sind. Offenbar kann GJ kleiner sein, als jede angebbare Grösse.
Es ist aber, wenn man sich Kreise durch A, B, G und durch A, b, g gezogen denkt, in denen AG und Ag, wegen der rechten Winkel bei B und b Durchmesser sind,
mithin
Da nun JG kleiner als jede angebbare Grösse angenommen werden kann, so kann man bewirken, dass AG und Ag ebenfalls um weniger, als jeden angebbaren Unterschied von einander abweichen. Demnach wird nach A. das Verhältniss
von dem einfachen
um weniger als jeder anggebbare Unterschied abweichen. Nach §. 1. hat man daher zuletzt:
2. Fall. Gibt man der Linie BD irgend eine beliebige Lage gegen AD, wie etwa die BD', so wird, wenn bd' ∥ BD'
und daher auch jetzt
3. Fall. Ist der Winkel D nicht gegeben, sondern convergirt die Linie BD nach irgend einem gegebenen Punkte hin, oder ist sie nach irgend einem Gesetze gezogen; so nähern sich doch die Winkel D und d immer mehr der Gleichheit und kommen einander näher, als jeder gegebene Unterschied. Demnach werden sie, nach §. 1. zuletzt einander gleich und es verhalten sich BD und bd wie früher. W. z. b. w.
| Zusatz 1. Da zuletzt die Tangenten | AD | und | Ad |
| die Bogen | AB | und | Ab |
| und die Sinusse | BC | und | bc |
den Sehnen AB und Ab gleich werden; so verhalten sich zuletzt auch ihre Quadrate, wie
Zusatz 2. Da
und zuletzt
so haben wir ebenfalls zuletzt
| und auch D. | ADB : Adb = AD³ : Ad³ = DB3/2 : db3/2 ABC : Abc = BC³ : bc³. |
Zusatz 3. Da zuletzt
so werden die krummlinigen Figuren ADB und Adb, nach der Natur der Parabeln[2], ⅔ der geradlinigen Figuren ADB und Adb, und die Segmente AB, Ab ⅓ derselben Dreiecke. Es verhalten sich demnach so wohl diese krummlinigen Figuren, als auch diese Segmente, wie
§. 12. Anmerkung. Bei allen diesen Behauptungen setzen wir übrigens voraus, dass der Berührungswinkel weder unendlich grösser, noch unendlich kleiner sei, als die Berührungswinkel, welche Kreise mit ihren Tangenten bilden, d. h. dass die Krümmung am Punkte A weder unendlich gross, noch unendlich klein sei und der Abstand AJ eine endliche Grösse habe.
Es kann nämlich DB proportional AD³ genommen werden, in diesem Falle kann kein Kreis durch den Punkt A zwischen der Tangente AD und der Curve AB gezogen werden und der Berührungswinkel wird unendlich kleiner als bei Kreisen sein. Aus einem ähnlichen Grunde erhält man, wenn man nach und nach DB proportional
annimmt, eine Reihe von ins Unendliche fortgehenden Berührungswinkeln entstehen, von denen jeder nachfolgende unendlich kleiner als der vorhergehende ist. Macht man dagegen nach und nach DB proportional
so erhält man eine Reihe von Berührungswinkeln, deren erster mit dem beim Kreise identisch, der zweite unendlich grösser und jeder folgende unendlich grösser als der vorhergehende ist. Aber auch zwischen je zwei von diesen Winkeln kann man eine Reihe anderer einfügen, welche nach beiden Seiten ins Unendliche fortgeht, und von denen jeder folgende unendlich grösser als der vorhergehende ist. Z. B. wenn zwischen den Gliedern AD² und AD³ die Reihe
eingeschaltet wird. Wiederum kann zwischen je zwei Gliedern dieser Reihe eine neue Reihe zwischenliegender Winkel eingeschaltet werden, welche von einander unendlich verschieden sind. Die Natur kennt hierin keine Grenze.
Was von krummen Linien und den durch sie begrenzten Flächen bewiesen worden ist, wird leicht auf die krummen Oberflächen fester Körper und auf diese selbst angewandt. Ich habe diese Lehnsätze vorausgeschickt, um künftig der weitläufigen Beweisführung mittelst des Widerspruchs, nach der Weise der alten Geometer, überhoben zu sein. Die Beweise werden nämlich kürzer durch die Methode der untheilbaren Grössen. Da aber die Methode des Untheilbaren etwas anstössig (durior) ist und daher für weniger geometrisch gehalten wird, so zog ich es vor, die Beweise der folgenden Sätze auf die letzten Summen und Verhältnisse verschwindender und auf die ersten werdender Grössen zu begründen, und desshalb habe ich die Beweise jener Grenzen mit möglichster Kürze vorausgeschickt. Durch sie wird dasselbe geleistet, was man durch die Methode des Untheilbaren erlangt, und wir werden um so sicherer uns der bewiesenen Principien bedienen können.
Wenn ich ferner in der Folge Grössen als aus kleinen Theilen bestehend betrachten, oder statt gerader unendlich kleine krumme Linien annehmen sollte; so wünsche ich, dass man darunter nicht untheilbare, sondern verschwindend kleine theilbare, nicht Summen und Verhältnisse bestimmter Theile, sondern die Grenzen der Summen und Verhältnisse verstehen und dass man den Kern solcher Beweise immer auf die Methode der hervorgehenden Lehnsätze zurückführen möge.
Man kann den Einwurf machen, dass es kein letztes Verhältniss verschwindender Grössen gebe, indem dasselbe vor dem Verschwinden nicht das letzte sei, nach dem Verschwinden aber überhaupt kein Verhältniss mehr stattfinde. Aus demselben Grunde könnte man aber auch behaupten, dass ein nach einem bestimmten Orte strebender Körper keine letzte Geschwindigkeit habe; diese sei, bevor er den bestimmten Ort erreicht hat, nicht die letzte, nachdem er ihn erreicht hat, existire sie gar nicht mehr. Die Antwort ist leicht. Unter der letzten Geschwindigkeit versteht man diejenige, mit welcher der Körper sich weder bewegt, ehe er den letzten Ort erreicht und die Bewegung aufhört, noch die nachher stattfindende, sondern in dem Augenblick, wo er den Ort erreicht, ist es die letzte Geschwindigkeit selbst, mit welcher der Körper den Ort berührt und mit welcher die Bewegung endigt. Auf gleiche Weise hat man unter dem letzten Verhältniss verschwindender Grössen dasjenige zu verstehen, mit welchem sie verschwinden, nicht aber das vor oder nach dem Verschwinden stattfindende. Eben so ist das erste Verhältniss entstehender Grössen dasjenige, mit welchem sie entstehen; die erste und letzte Summe diejenige, mit welcher sie anfangen oder aufhören zu sein (entweder grösser oder kleiner zu werden). Es existirt eine Grenze, welche die Geschwindigkeit am Ende der Bewegung erreichen, nicht aber überschreiten kann; dies ist die letzte Geschwindigkeit. Dasselbe gilt von der Grenze aller anfangenden und aufhörenden Grössen und Proportionen. Da diese Grenze fest und bestimmt ist, so ist es eine wahrhaft geometrische Aufgabe, sie aufzusuchen. Alles Geometrische wird aber mit Fug und Recht bei andern geometrischen Bestimmungen und Beweisen in Anwendung gebracht.
Es kann auch behauptet werden, wenn die letzten Verhältnisse verschwindender Grössen gegeben sind, werde auch ihre letzte Grösse gegeben und es bestehe so jede Grösse aus untheilbaren Stücken, wovon Euklid im 10. Buche seiner Elemente das Gegentheil erwiesen hat. Dieser Einwurf stützt sich jedoch auf eine falsche Veraussetzung. Jene letzten Verhältnisse, mit denen die Grössen verschwinden, sind in der Wirklichkeit nicht die Verhältnisse der letzten Grössen, sondern die Grenzen, denen die Verhältnisse fortwährend abnehmender Grössen sich beständig nähern, und denen sie näher kommen, als jeder angebbare Unterschied beträgt, welche sie jedoch niemals überschreiten und nicht früher erreichen können, als bis die Grössen ins Unendliche verkleinert sind. Deutlicher ist die Sache bei unendlich grossen Grössen einzusehen. Werden zwei Grössen, deren Unterschied gegeben ist, in’s Unendliche vermehrt, so ist ihr letztes Verhältniss gegeben, nämlich das der Gleichheit; jedoch werden damit nicht die letzten oder allergrössten Grössen, deren Verhältniss jenes ist, gegeben.
Wenn ich daher in der Folge, um eine leichte Darstellung der Dinge zu benutzen, von sehr kleinen, verschwindenden oder letzten Grössen sprechen sollte; so verstehe man darunter nicht Grössen, welche ihrer Grösse nach bestimmt sind, sondern solche, die unbegrenzt verkleinert werden müssen.
Bemerkungen und Erläuterungen [des Übersetzers]
- ↑ [578]
No. 2. S. 52. Setzt man den Bogen AB = α, Ab = β, so wird für den Radius AM = 1, BD = AC = sin vers. α = 1 – cos. α = 2 sin ½α² AB = 2 sin AGB = 2 sin ½α und eben so bd = 2 sin ½β²; Ab = 2 sin ½β. Werden nun α und β verschwindend klein, so wird BD = ½α², AB = α, bd = ½β², Ab = β, demnach jetzt: AB² : Ab² = α² : β² = BD : bd.
- ↑ [578] No. 3. S. 52. Weil , so wird AD² = Constans. DB, und daher für AC = DB als Abscisse, BC = AD die zugehörige Ordinate in einer Parabel. Ferner ist nach den Gesetzen der Parabel die krummlinige Figur ABC = ⅔ ACBD und daher die krummlinige Figur ABD = ⅓ ABCD = ⅔ Δ ABD.
Anmerkungen (Wikisource)
| ← Grundsätze oder Gesetze der Bewegung | Nach oben | Buch I. Abschnitt II. → |
| Fertig! Dieser Text wurde zweimal anhand der Quelle Korrektur gelesen. Die Schreibweise folgt dem Originaltext. |