Mathematische Principien der Naturlehre/Buch1-III

← Buch I. Abschnitt II.

Mathematische Principien der Naturlehre (1872) von Isaac Newton, übersetzt von Jakob Philipp Wolfers Buch I. Abschnitt III.

Buch I. Abschnitt IV. →

ABSCHNITT III.

Von der Bewegung der Körper in excentrischen Kegelschnitten.

---

Fig. 24.

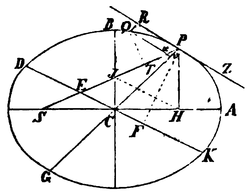
§. 29. Aufgabe. Ein Körper bewegt sich in einer Ellipse; man sucht das Gesetz der nach ihrem Brennpunkt gerichteten Centripetalkraft.

Es sei S der Brennpunkt der Ellipse. Man ziehe SP, welche den Durchmesser DK in E und die Ordinate Qv in x schneidet und vollende das Parallelogramm QxPR. Offenbar ist

EP = AC.

Zieht man nämlich aus dem zweiten Brennpunkte H

HJ ∥ EC,

so wird, weil

CH = CS

auch

EJ = ES,

und

EP	= EJ + JP = ½(2EJ + 2JP)
	= ½(ES + EJ + JP + JP)
EP	= ½(SP + JP).

Da aber

HJ ∥ RP,

so wird

$\scriptstyle \angle$ PJH = JPR = HPZ = PHJ,

also

JP = PH

und

1.     EP = ½(SP + PH) = AC.

Fällt man nun auf SP das Perpendikel QT, und setzt man den Parameter der Ellipse

2.     $\scriptstyle {\frac {2\cdot BC^{2}}{AC}}=L$,

so hat man

L · QR : L · Pv = PE : PC = AC : PC

ferner

L · Pv : Gv · Pv = L : Gv,

also durch Verbindung beider Proportionen

3.     L · QR : Gv · Pv = L · AC : Gv · PC.

Da aber auch

Gv · Pv : Qv² = PC² : CD²

so wird

4.     L · QR : Qv² = L · AC · PC : Gv · CD².

Nach §. 8. wird beim Zusammenfallen der Punkte Q und P

Qv² = Qx²,

daher auch

5.     L · QR : Qx² = L · AC · PC : Gv · CD².

Ferner ist

Qx² : QT² = PE² : PF², wo PF auf CK vertikal,

und nach §. 26.

PE² : PF² = DC² : CB²

demnach

L · QT : QT² = L · AC · PC : Gv · CB²

oder da

L · AC = 2 · BC² (Gl. 2.)

6.     L · QR : QT² = 2PC : Gv.

Fallen die Punkte Q und P zusammen, so wird

2 · PC = Gv,

mithin (nach Gl. 6.) in diesem Falle

7.     L · QR = QT²

und indem man auf beiden Seiten mit $\scriptstyle {\frac {SP^{2}}{QR}}$ multiplicirt.

8.     $\scriptstyle {\frac {SP^{2}\cdot QT^{2}}{QR}}$ = L · SP².

Nach §. 21., Zusatz 1. und 5. ist daher die Centripetalkraft

L · SP²,

oder weil L constant ist,

SP²

indirect proportional.

Zweiter Beweis. Da die nach dem Mittelpunkte der Ellipse gerichtete Kraft, vermöge welcher der Körper P sich auf jener bewegen kann, (nach §. 27., Zusatz 1.) dem Abstande PC des Körpers vom Mittelpunkte proportional ist; so ziehe man CE der Tangente PR parallel. Alsdann wird die Kraft, vermöge welcher derselbe Körper P sich um irgend einen andern Punkt S in der Ellipse bewegen kann, wenn CE und PS sich in E schneiden, (nach §. 22. Zusatz 3.)

$\scriptstyle {\frac {PE^{3}}{PS^{2}}}$,

d. h. wenn S der Brennpunkt der Ellipse, also PE constant ist, indirect

PS²

proportional.

Mit derselben Kürze, mit welcher wir §. 27. auf die Parabel und Hyperbel übertragen haben, könnten wir dies auch bei dem vorliegenden §. ausführen; allein wegen der Wichtigkeit der Aufgabe und ihrer häufigen Anwendung in der Folge wird es nicht unpassend sein, diese andern Fälle durch besondere Beweise zu bestätigen.

§. 30. Aufgabe. Ein Körper bewegt sich in einer Hyperbel, man sucht das Gesetz der nach ihrem Brennpunkte gerichteten Centripetalkraft.

Fig. 25.

Es seien CA und CB die halben Axen der Hyperbel, PG und KD conjugirte Durchmesser, PF ein auf den letzteren gefälltes Perpendikel und Qv die Ordinate des Punktes Q zum Durchmesser GP als Abscissenaxe. Man ziehe SP, welche den Durchmesser DK in E und die Ordinate Qv in x schneidet, und vollende das Parallelogramm QRPx. Offenbar ist

EP = AC.

Zieht man nämlich vom andern Brennpunkt H

HJ ∥ EC,

so wird, weil

CS = CH

auch

ES = EJ;

mithin

EP = ES – PS	= ½(2 · ES – 2 · PS) = ½(EJ + EP – PS – PS)
	=½(PJ – PS).

Da aber

HJ ∥ PR,

also

$\scriptstyle \angle$ PJH = ZPJ = RPH = PHJ

JP = PH

und so

1.     EP = ½(PH – PS) = CA.

Auf SP fälle man das Perpendikel QT, alsdann ist, wenn man den Haupt-Parameter der Hyperbel

2.     $\scriptstyle {\frac {2\cdot BC^{2}}{CA}}=L$

setzt

L · QR : L · Pv = QR : Pv = Px : Pv = PE : PC = AC : PC

ferner

L · Pv : Gv · vP = L : Gv

also

3.     L · QR : Gv · Pv = L · AC : Gv · PC.

Da nun

Gv · Pv : Qv² = PC² : CD²

so wird

4.     L · QR : Qv² = L · AC · PC : Gv · CD²,

und weil nach §. 8., wenn Q und P zusammenfallen,

Qv = Qx,

auch

5.     L · QR : Qx² = L · AC · PC : Gv · CD².

Ferner ist

Qx² : QT² = EP² : PF² = CA² : PF² = CD² : CB² (§. 26.)

also

L · QR : QT² = L · AC · PC : Gv · CB²

und weil

L · AC = 2 · BC² (Gl. 2.)

6.     L · QR : QT² = 2 · PC : Gv.

Fallen die Punkte P und Q zusammen, so wird

2 · PC = Gv,

mithin in diesem Falle (nach GL 6.)

7.     QT² = L · QR,

und indem man auf beiden Seiten durch $\scriptstyle {\frac {SP^{2}}{QR}}$ multiplicirt

8.     $\scriptstyle {\frac {QT^{2}\cdot SP^{2}}{QR}}$ = L · SP².

Nach §. 21., Zusatz 1. und 5. ist daher die Centripetalkraft

L · SP²,

oder weil L constant ist,

SP²

indirect proportional.

Zweiter Beweis. Man suche die Kraft, welche nach dem Mittelpunkte C der Hyperbel gerichtet ist; dieselbe ist dem Abstande CP proportional (§. 27., Zusatz 1.). Alsdann wird (nach §. 22., Zusatz 3.) die nach dem Brennpunkte S gerichtete Kraft

$\scriptstyle {\frac {PE^{3}}{PS^{2}}}$,

d. h. weil PE constant ist,

PS²

indirect proportional.

Eben so wird bewiesen, dass, wenn die Centripetalkraft in eine Centrifugalkraft verwandelt ist, der Körper sich in der entgegengesetzten Hyperbel bewege.

§. 31. Lehnsatz. Der Parameter einer Parabel, welcher sich auf einen beliebigen Scheitelpunct bezieht, ist dem vierfachen Abstand jenes Scheitels vom Brennpunkte gleich.

Bekannt aus der Lehre von den Kegelschnitten.^[1]

Fig. 26.

§. 32. Lehnsatz. Das Perpendikel, welches vom Brennpunkte einer Parabel auf eine Tangente gefällt wird, ist die mittlere Proportinallinie zwischen der Entfernung des Brennpunktes vom Berührungspunkte und der Entfernung des erstern vom Hauptscheitelpunkte.

Es sei AQP eine Parabel, S ihr Brennpunkt, P ein Berührungspunkt, PO die Ordinate desselben, AO die Axe, PM die Tangente, welche die Axe in M schneidet, endlich SN das Perpendikel von S auf PM. Man ziehe AN. Da nun

MS = PS,

MN = NP,

und

MA = AO;^[2]

so ist

AN ∥ PO

und

$\scriptstyle \angle$ SAN = 90°;

also

Δ SAN ∼ SMN ∼ SPN

und

PS : SN = SN : SA.     W. z b. w.

Zusatz 1. Es ist

PS² : SN² = PS : SA.

Zusatz 2. Da SA constant, so ist SN² proportional PS.

Zusatz 3. Der Durchschnittspunkt der beliebigen Tangente PM mit dem aus dem Brennpunkte S auf sie gefällten Perpendikel SN fällt in die gerade Linie AN, welche die Parabel im Hauptscheitelpunkte A berührt.

§. 33. Aufgabe. Ein Körper bewegt sich auf einer Parabel; man sucht das Gesetz der nach dem Brennpunkte gerichteten Centripetalkraft. In der Figur des vorhergehenden Paragraphen sei P der Körper auf dem Umfange der Parabel, und man ziehe vom Punkte Q, wohin er zunächst gelangen wird,

QR ∥ SP

QT senkrecht auf SP

und

Qv ∥ PM,

wobei Qv den Durchmesser YPG in v und den Radius PS in x schneidet. Da nun

Δ Pxv ∼ MSP

und

SM = SP,

so ist auch

1.     Pv = Px = RQ.

Nach §. 31. ist aber

Qv² = 4PS · Pv = 4PS · QR.

Fallen nun die Punkte P und Q zusammen, so wird nach §. 8.

Qv = Qx

und in diesem Falle

2.     Qx² = 4PS · QR.

Da aber

Δ QxT ∼ PSN,

so haben wir

Qx² : QT²	= PS² : SN²
	= PS : AS (§. 32., Zusatz 1.)
	= 4PS · QR : 4AS · QR

also, da nach Gl. 2.

Qx² = 4PS · QR, auch

3.     QT² = 2PS · QR.

Indem man auf beiden Seiten der Gl. 3. durch $\scriptstyle {\frac {SP^{2}}{QR}}$ multiplicirt, wird

4.     $\scriptstyle {\frac {SP^{2}\cdot QT^{2}}{QR}}$ = 4AS · PS²,

also nach §. 21., Zusatz 1. und 5. die Centripetalkraft 4AS · PS²
oder weil

4AS constant ist,

PS²

indirect proportional.

Zusatz 1. Aus den drei letzten Aufgaben (§. 29, 30. und 33.) ergiebt sich Folgendes. Geht ein Körper P vom Punkt P ans längs der beliebigen geraden Linie PR mit irgend einer Geschwindigkeit fort, und wirkt auf ihn zugleich eine Centripetalkraft ein, welche dem Quadrat seines Abstandes vom Mittelpunkte der Kräfte indirect proportional ist; so bewegt sich dieser Körper in einem Kegelschnitte, dessen Brennpunkt im Centrum der Kräfte liegt, und umgekehrt. Ist nämlich der Brennpunkt, der Berührungspunkt und die Lage der Tangente gegeben; so kann man einen Kegelschnitt beschreiben, welcher in jenem letztern Punkte eine gegebene Krümmung hat. Die Krümmung wird aber durch die gegebene Centripetalkraft und die Geschwindigkeit des Körpers bekannt und zwei sich wechselseitig berührende Bahnen können nicht vermöge derselben Centripetalkraft und bei derselben Geschwindigkeit beschrieben werden.

Zusatz 2. Ist die Geschwindigkeit, mit welcher der Körper von seinem Orte P ausgeht, so gross, dass die kleine Linie PR in irgend einem sehr kleinen Zeittheilchen beschrieben werden kann, und die Centripetalkraft vermögend ist, ihn in derselben kleinen Zeit durch den kleinen Raum QR zu bewegen, so beschreibt der Körper einen Kegelschnitt, dessen Parameter

$\scriptstyle ={\frac {QT^{2}}{QR}}$,

von QT und QR beide als in’s Unendliche verkleinert gedacht werden.

Den Kreis zähle ich hier zur Ellipse, und nehme denjenigen Fall aus, in welchem sich der Körper geradlinig gegen das Centrum der Kräfte bewegt.

§. 34. Lehrsatz. Bewegen sich mehrere Körper um ein gemeinschaftliches Centrum, und nimmt die Centripetalkraft indirect im doppelten Verhältniss der Entfernung vom Centrum ab; so stehen die Parameter der Bahnen im doppelten Verhältniss derjenigen Flächen, welche die Körper mit den nach dem Centrum gezogenen Radien gleichzeitig beschreiben.

Nach §. 33., Zusatz 2. ist nämlich der Parameter

$\scriptstyle L={\frac {QT^{2}}{QR}}$,

wo QT und QR die letzten Werthe beim Zusammenfallen der Punkte P und Q haben. Die sehr kleine Linie QR ist aber, bei gegebener Zeit, der sie erzeugenden Kraft, d. h. nach der Voraussetzung

SP²

indirect proportional. Es ist daher

$\scriptstyle {\frac {QT^{2}}{QR}}$ proportional QT² · SP²,

d. h. der Parameter steht im doppelten Verhältniss der Fläche QT · SP.

Zusatz. Hieraus folgt, dass der ganze Flächeninhalt einer Ellipse und das ihm proportionale Rechteck über beiden Axen im zusammengesetzten Verhältniss der Quadratwurzel aus dem Parameter und der Umlaufszeit stehen^[3]. Die ganze Fläche ist nämlich dem Produkt aus der in einer gegebenen Zeit beschriebenen Fläche

QT · SP

in die Umlaufszeit proportional.

§. 35. Lehrsatz. Unter denselben Voraussetzungen wird die Umlaufszeit der 3/2ten Potenz der grossen Axe proportional sein.

Sind 2a und 2b bezüglich die grosse und kleine Axe einer Ellipse, so ist

2a : 2b = 2b : L

also

$\scriptstyle 2b={\sqrt {2aL}}$

2a · 2b = (2a)3/2 $\scriptstyle {\sqrt {L}}$,

also

4ab proportional (2a)3/2 $\scriptstyle {\sqrt {L}}$; aber nach §. 34. Zusatz
4ab auch proportional T$\scriptstyle {\sqrt {L}}$,

mithin ist T proportional (2a)3/2.     W. z. b. w.

Zusatz. Die Umlaufszeiten in Ellipsen sind daher denjenigen in Kreisen gleich, wenn die Durchmesser der letztern den grossen Axen der erstern gleich sind.

§. 36. Lehrsatz. Ist wieder dasselbe vorausgesetzt, zieht man ferner durch den Ort der Körper Linien, welche daselbst die Bahn berühren und fällt man endlich Perpendikel vom gemeinschaftlichen Brennpunkte auf diese Tangenten; so sind die Geschwindigkeiten zusammengesetzt

den Perpendikeln indirect

und der Quadratwurzel aus dem Parameter

direct proportional.

Fig. 27.

Fällt man aus dem Brennpunkt S das Perpendikel SY auf die Tangente PR, so soll die Geschwindigkeit des Körpers

$\scriptstyle {\frac {\sqrt {L}}{SY}}$

proportional sein.

Dieselbe ist nämlich dem sehr kleinen, im gegebenen Zeittheilchen beschriebenen, Bogen PQ, d. h. nach §. 7. der Tangente proportional. Da nun

PR : QT = PS : SY,

so ist jene Geschwindigkeit

$\scriptstyle {\frac {QT\cdot PS}{SY}}$ proportional

und nach §. 34.

QT · PS proportional $\scriptstyle {\sqrt {L}}$.     W. z. b. w.

Zusatz 1. Die Parameter stehen im zusammengesetzten doppelten Verhältniss der Perpendikel auf die Tangenten und der Geschwindigkeiten.

Zusatz 2. Die Geschwindigkeiten der Körper in dem grössten und kleinsten Abstande vom gemeinschaftlichen Brennpunkte, sind indirect den Abständen und direct der Quadratwurzel aus dem Parameter proportional. In diesem Falle sind nämlich Entfernung und Perpendikel identisch.

Zusatz 3. Daher verhält sich die Geschwindigkeit auf dem Kegelschnitt, im grössten oder kleinsten Abstande vom Brennpunkte, zu der Geschwindigkeit auf einem Kreise, dessen Halbmesser gleich diesem grössten oder kleinsten Abstande ist, wie die Quadratwurzel aus dem Parameter zur Quadratwurzel aus dem doppelten Abstande.^[4]

Zusatz 4. Die Geschwindigkeiten solcher Körper, welche sich in Ellipsen bewegen, sind im mittleren Abstande vom gemeinschaftlichen Brennpunkte dieselben, welche Körper besitzen, die sich in Kreisen von diesem mittlern Abstande als Halbmesser bewegen. Nach §. 18., Zusatz 6. sind sie also den Quadratwurzeln aus diesen Abständen indirect proportional.

Die Perpendikel sind nämlich hier gleich den halben kleinen Axen und diese verhalten sich wie die mittlern Proportionalen zwischen den Parametern und den Abständen. Setzt man dieses Verhältniss indirect mit dem halben Verhältniss der Parameter, direct genommen, zusammen, so entsteht das indirecte Verhältniss der Quadratwurzeln aus den Abständen.^[5]

Zusatz 5. In derselben oder in gleichen Figuren, oder auch in ungleichen Figuren, deren Parameter gleich sind, ist die Geschwindigkeit dem vom Brennpunkte auf die Tangente gefällten Perpendikel indirect proportional.

Zusatz 6. In der Parabel verhält sich die Geschwindigkeit indirect, wie die Quadratwurzel aus der Entfernung vom Brennpunkt; in der Ellipse ist das Verhältniss grösser, in der Hyperbel kleiner. Nach §. 32., Zusatz 2. verhält sich nämlich das vom Brennpunkte auf die Tangente gefällte Perpendikel wie die Quadratwurzel aus dem Abstande, in der Hyperbel variirt es weniger, in der Ellipse mehr.

Zusatz 7. In der Parabel verhält sich in einem beliebigen Abstande vom Brennpunkte die Geschwindigkeit eines Körpers zu der in einem Kreise, dessen Halbmesser dem Abstande gleich ist, wie

$\scriptstyle {\sqrt {2}}:1$.

In der Ellipse ist das Verhältniss kleiner und in der Hyperbel grösser. Nach Zusatz 2. steht nämlich die Geschwindigkeit im Scheitel der Parabel in diesem Verhältniss, und nach Zusatz 6., wie auch nach §. 18., Zusatz 6. bleibt das Verhältniss in allen Abständen dasselbe. Daher ist auch die Geschwindigkeit in der Parabel gleich der in einem Kreise, dessen Halbmesser halb so gross als der Abstand in der Parabel ist. In der Ellipse ist sie kleiner, in der Hyperbel grösser.

Zusatz 8. Die Geschwindigkeit in einem beliebigen Kegelschnitt verhält sich zu der in einem Kreise, dessen Halbmesser dem halben Parameter gleich ist, wie dieser Halbmesser zum Perpendikel vom Brennpunkte auf die Tangente des Kegelschnittes. Dies folgt aus Zusatz 5.

Zusatz 9. Da nach §. 18., Zusatz 6. die Geschwindigkeit in diesem Kreise sich zu der in einem andern Kreise indirect wie die Quadratwurzeln aus den Radien verhält, so wird sich auch die Geschwindigkeit in dem Kegelschnitt verhalten zu der Geschwindigkeit in einem Kreise, dessen Halbmesser gleich dem Abstand in jenem ist, wie die mittlere Proportionale zwischen jenem gemeinschaftlichen Abstande und dem halben Parameter zu dem Perpendikel, welches vom gemeinschaftlichen Brennpunkte auf die Tangente des Kegelschnittes gefällt wird.^[6]

§. 37. Aufgabe. Die Centripetalkraft ist indirect dem Quadrate des Abstandes vom Centrum proportional, und man kennt die absolute Grösse jener Kraft; man sucht die Linie, welche ein Körper beschreibt, der von einem gegebenen Orte, mit gegebener Geschwindigkeit und nach gegebener Richtung ausgeht.

Fig. 28.

Die nach dem Punkte S gerichtete Centripetalkraft sei so beschaffen, dass sie der Körper p in der beliebigen Bahn pq wandern lässt und man kenne seine Geschwindigkeit im Punkte p. Vom Punkte P gehe der Körper längs PR mit gegebener Geschwindigkeit aus, und werde dann durch die Centripetalkraft in den Kegelschnitt PQ gebracht. Die letztere Curve wird daher durch PR im Punkte P berührt. Eben so berühre pr die Curve pq in p. Denkt man sich von S auf beide Tangenten Perpendikel gefällt, so steht nach §. 36., Zusatz 1. der Parameter des Kegelschnittes zu dem der gegebenen Curve in einem Verhältniss, welches aus dem Quadrat der Perpendikel und dem der Geschwindigkeiten zusammengesetzt ist; ersterer ist mithin gegeben und sei = L.

Ferner ist der Brennpunkt S des Kegelschnitts gegeben, und setzt man $\scriptstyle \angle$ RPH = 180° – RPS, so ist die Richtung der Linie PH, in welcher der andere Brennpunkt H liegt, bekannt. Zieht man nun SK perpendikulär auf PH, so ist

1.     SH²	= 4CH² = 4BH² – 4BC²
	= (SP + PH)² – L(SP + PH)
	= SP² + 2SP · PH + PH² – L(SP + PH)

Da nun auch

2.     SH² = SP² + PH² – 2PH · PK,

so wird

– 2PH · PK = 2SP · PH – L(SP + PH)

oder

L · (SP + PH) = 2PH (PS + PK)

endlich

3.     SP + PH : PH = 2(PS + PK) : L.

Mithin ist PH der Lage und Grösse nach bekannt. Ist die Geschwindigkeit des Körpers in P so beschaffen, dass

L < 2(PS + PK)

also auch

PH < SP + PH,

so liegt PH auf derselben Seite der Tangente PR, auf welcher die Linie PS liegt, die Figur ist eine Ellipse und die grosse Axe = SP + PH bekannt.

Ist die Geschwindigkeit des Körpers der Art, dass

L = 2(PS + PK)

also auch

PH = PH + PS,

so wird PH = ∞, die Figur eine Parabel, deren Axe

SH ∥ PK

und daher bekannt.

Ist endlich

L > 2(PS + PK),

also auch

PH > PH + PS;

so muss PH auf der andern Seite der Tangente angenommen werden, und da die letztere zwischen beiden Brennpunkten durchgesetzt, wird die Figur eine Hyperbel, deren Hauptaxe

= SP – PH oder PH – PS,

also bekannt.

Bewegt sich nämlich der Körper in diesen Fällen in einem so gefundenen Kegelschnitte; so ist nach §. 29., 30. und 32. die Centripetalkraft dem Quadrat der Entfernung des Körpers vom Centrum indirect proportional. Es wird daher die Linie PQ, welche er vermöge einer solchen Kraft beschreibt, richtig dargestellt, wenn er vom gegebenen Orte P aus mit gegebener Geschwindigkeit längs der ihrer Lage nach gegebenen geraden Linie PR fortgeht.

Zusatz 1. Hiernach wird man in jedem Kegelschnitte aus dem gegebenen Hauptscheitelpunkte D, dem Parameter L und dem Brennpunkte S den andern Brennpunkt H finden können. Die Proportion 3.

SP + PH · PH = 2(PS + PK) : L

wird nämlich in diesem Falle

SD + DH : DH	= 2(PS + DS) : L
	= 4DS : L

und hieraus

SD : DH = 4DS – L : L,

wodurch DH bekannt wird.

Zusatz 2. Ist daher die Geschwindigkeit des Körpers im Hauptscheitelpunkte D gegeben, so findet man leicht die ganze Bahn.

Nimmt man nämlich nach §. 36., Zusatz 3.

L : 2DS

wie das Quadrat der gegebenen Geschwindigkeit zum Quadrate der Geschwindigkeit in einem Kreise, dessen Halbmesser = DS; so erhält man DS. Hierauf aus

SD : DH = 4DS – L : L

auch DH.

Zusatz 3. Bewegt sich der Körper in einem beliebigen Kegelschnitte, und wird er durch irgend einen Anstoss aus seiner Bahn gebracht, so kann man diejenige Bahn kennen lernen, in welcher er nachher seinen Lauf fortsetzen wird.

Setzt man nämlich die eigene Bewegung des Körpers mit derjenigen zusammen, welche der Anstoss allein hervorbringen würde, so erhält man die Bewegung, mit welcher der Körper von dem gegebenen Orte des Anstosses aus, nach einer gegebenen geraden Linie fortgehen wird.

Zusatz 4. Wird der Körper durch irgend eine, von aussen her einwirkende Kraft beständig gestört, so wird sein Lauf sehr nahe bekannt, indem man die Aenderungen bestimmt, welche jene Kraft in einigen Punkten hervorbringt und aus der Analogie der Reihe, die fortwährenden Aenderungen in den zwischenliegenden Punkten abschätzt.

Fig. 29.

§. 37a. Anmerkung. Wenn ein Körper P, vermöge einer nach einem beliebigen Punkte R gerichteten Centripetalkraft, sich auf dem Umfange irgend eines gegebenen Kegelschnittes bewegt, dessen Mittelpunkt in C liegt und man das Gesetz dieser Centripetalkraft sucht; so ziehe man CG dem Radius Vector RP parallel, und verlängere erstere bis sie die in P an der Bahn gezogene Tangente PG in G schneidet. Alsdann ist jene Kraft (nach §. 27., Zusatz 1., §. 28. und §. 22., Zusatz 3.) proportional

$\scriptstyle {\frac {CG^{3}}{RP^{2}}}$.

Bemerkungen und Erläuterungen [des Übersetzers]

1. 

   Fig. 229.

   No. 17. S. 73. Ist A der Hauptscheitelpunkt der Parabel, S ihr Brennpunkt, P ein anderer Scheitelpunkt, x' die Abscisse, y' die Ordinate, beide auf den letzteren Scheitelpunkt bezogen; so hat man bekanntlich $\scriptstyle y'^{2}={\frac {2p}{\sin \ \alpha ^{2}}}x'$. Es ist aber $\scriptstyle tg\alpha ={\frac {p}{b}}$, also $\scriptstyle {\frac {2p}{\sin \ \alpha ^{2}}}=2p\cdot {\frac {b^{2}+p^{2}}{p^{2}}}={\frac {2p\left(2ap+p^{2}\right)}{p^{2}}}=4\left(a+{\frac {p}{2}}\right)$ und da $\scriptstyle r^{2}=b^{2}+\left({\frac {p}{2}}-a\right)^{2}=2ap+{\frac {p^{2}}{4}}-pa+a^{2}=\left(a+{\frac {p}{2}}\right)^{2}$ also $\scriptstyle r=a+{\frac {p}{2}}$, so wird $\scriptstyle {\frac {2p}{\sin \ \alpha ^{2}}}=4r$.
2. No. 18. S. 73. Ist wie vorhin PO = b, AO = a (Fig. 26.), so wird als Subtangente $\scriptstyle MO={\frac {b}{tga}}={\frac {b^{2}}{p}}={\frac {2ap}{p}}=2a$, mithin MA = AO = a. Ferner ist SP = r = a + $\scriptstyle {\frac {p}{2}}$ = AM + AS = MS, endlich da MSP gleichschenklig und SN (Fig. 26.) perpendikular auf MP, so ist MN = NP.
3. No. 19. S. 76. Wegen der Proportionalität zwischen den Zeiten und den in ihnen beschriebenen Flächenräumen, möge die Fläche OT · SP in der Zeiteinheit beschrieben sein, die ganze Fläche E der Ellipse in T solchen Einheiten beschrieben werden; alsdann ist 1 : T = QT · SP : E also E = T · QT · SP = T$\scriptstyle {\sqrt {L}}$.
4. No. 20. S. 77. Ist dieser grösste oder kleinste Abstand = c, so ist die Geschwindigkeit im Kegelschnitt $\scriptstyle {\frac {\sqrt {L}}{c}}$ proportional, im betreffenden Kreise ist der Parameter = 2c, mithin die Geschwindigkeit in demselben $\scriptstyle {\frac {\sqrt {2c}}{c}}$ proportional; es verhält sich daher die erstere Geschwindigkeit zur letzteren, wie $\scriptstyle {\sqrt {L}}:{\sqrt {2c}}$.
5. 

   Fig. 230.

   No. 21. S. 77. Die Abstände Sc und SC sind respective a und A, die Perpendikel Sd und SD b und B, die Parameter l und L hier $\scriptstyle {\frac {2b^{2}}{a}}$ und $\scriptstyle {\frac {2B^{2}}{A}}$, die Geschwindigkeiten v und V; demnach $\scriptstyle v:V={\frac {\sqrt {2}}{b}}:{\frac {\sqrt {L}}{B}}={\frac {b{\sqrt {2}}}{b{\sqrt {a}}}}:{\frac {B{\sqrt {2}}}{B{\sqrt {A}}}}={\frac {1}{\sqrt {a}}}:{\frac {1}{\sqrt {A}}}$ und auch $\scriptstyle b:B={\sqrt {1a}}:{\sqrt {LA}}=b{\sqrt {{\frac {2}{a}}a}}:B{\sqrt {{\frac {2}{A}}A}}$.
6. No. 22. S. 78. Ist der Parameter = p, die Geschwindigkeit im Kegelschnitt = V, die im ersten Kreise = k, die im zweiten = K, der Abstand in diesem und im Kegelschnitt = r, das Perpendikel auf die Tangente = T; so hat man, nach Zusatz 8. V : k = ½p : T nach §. 18., Zusatz 6. $\scriptstyle k:K={\frac {1}{\sqrt {{\frac {1}{2}}p}}}:{\frac {1}{\sqrt {r}}}$, mithin $\scriptstyle V:K={\sqrt {{\frac {1}{2}}p}}:{\frac {T}{\sqrt {r}}}={\sqrt {{\frac {1}{2}}p\cdot r}}:T$.

← Buch I. Abschnitt II.

Nach oben

Buch I. Abschnitt IV. →

{{{ANMERKUNG}}}

Fertig! Dieser Text wurde zweimal anhand der Quelle Korrektur gelesen. Die Schreibweise folgt dem Originaltext.