Die Excentricität der Erde scheint aber etwas grösser zu sein, und vergrössert man sie, so muss diese Gleichung in demselben Verhältniss annehmen. Setzt man daher die Excentricität = 1611/12, so wird die grösste Gleichung = 11′ 51″.
Ich habe auch gefunden, dass im Perihel der Erde das Apogeum und die Knoten des Mondes, wegen der grösseren Kraft der Sonne, geschwinder als im Aphel fortgingen, und zwar im umgekehrten dreifachen Verhältniss des Abstandes der Erde von der Sonne. Hieraus schliesst man, dass die jährlichen Gleichungen dieser Bewegungen der Mittelpunktsgleichung der Sonne proportional sind. Nun steht die Bewegung der Sonne im umgekehrten doppelten Verhältniss des Abstandes der Erde von ihr, und es beträgt die grösste Mittelpunktsgleichung, welche durch diese Ungleichheit hervorgebracht wird, 1° 56′ 20″, was mit der oben erwähnten Excentricität von 0,01611/12 = 0,016917 übereinstimmt.
Stände die Bewegung der Sonne im umgekehrten dreifachen Verhältniss des Abstandes, so würde diese Ungleichheit 2° 54′ 30″[1] als grösste Gleichung hervorbringen. Die grössten Gleichungen, welche durch die ungleichen Bewegungen des Apogeums und der Knoten des Mondes hervorgebracht werden, verhalten sich also zu 2° 54′ 30″, wie die mittlere tägliche Bewegung der zwei letzteren, zur mittleren täglichen Bewegung der Sonne.
Hieraus folgt, dass die grösste Gleichung der mittleren Bewegung des Apogeums 19′ 43″, die grösste Gleichung der mittleren Bewegung der Knoten 9′ 24″ beträgt.[2] Die erstere ist additiv und die letztere subtractiv, wenn die Erde vom Perihel zum Aphel fortschreitet; das Gegentheil findet statt, wenn sie sich im entgegengesetzten Theile der Bahn befindet.
Durch die Theorie der Schwere ist es gewiss, dass die Wirkung der Sonne auf den Mond ein wenig stärker ist, wenn die grosse Axe der Mondbahn durch die Sonne geht, als wenn dieselbe auf die, die Sonne und Erde verbindende gerade Linie senkrecht ist; folglich wird die Mondbahn im ersten Falle etwas weiter sein, als im letzteren.[3] Hieraus erhält man eine andere Gleichung der mittleren Bewegung des Mondes, welche von der Lage des Mond-Apogeums in Bezug auf die Sonne abhängt, und dieselbe hat ihren grössten Werth, wenn jenes Apogeum sich mit der Sonne im Octanten befindet; sie verschwindet hingegen, wenn dasselbe zu den Syzygien oder den Quadraturen gelangt. Sie wird zur mittleren Bewegung addirt, wenn das Mond-Apogeum von der Quadratur der Sonne zur Syzygie übergeht, im entgegengesetzten Falle wird sie subtrahirt. Diese Gleichung, welche ich die halbjährige nennen werde, steigt in den Octanten, wo sie am grössten ist, auf ungefähr 3′ 45″, so weit ich aus den Beobachtungen habe schliessen können. Dies ist ihr Werth in der mittleren Entfernung der Sonne von der Erde, sie muss aber im umgekehrten dreifachen Verhältniss jener Entfernung vermehrt oder vermindert werden, und beträgt daher in der
- ↑ [639] No. 272. S. 444. Der Werth der grössten Mittelpunktsgleichung der Sonne, für den mittlern Abstand der Erde = a, ist im Text = 1° 56′ 20″ = M angesetzt, wobei wir bemerken, dass Hansen a. a. O. M = 1° 55′ 27,″6 hat. Für den Abstand a + x, wird M' = M + Δ'M = M · ; M'' = M + Δ''M = M · also Δ'M : Δ''M = 2 : 3 und Δ''M = 3/2Δ'M. Wenn nun Δ'M die wahre Aenderung von M und Δ''M die hypothetische Aenderung desselben ist, so können wir M + Δ'M = 1° 56′ 20″ oder für M = o, Δ'M = 1° 56′ 20″ setzen und erhalten dann M'' = Δ''M = 3/2(1° 56′ 20″) = 2° 54′ 30″.
- ↑ [639] No. 273. S. 444. Setzt man die grösste Gleichung der mittlern täglichen Bewegung des Apogeums = ΔAp., die des Knotens = ♌, so hat man, auch Hansen a. a. O.
ΔAp. : 2° 54′ 30″ = 6′41,″0 rechtl. : 59′ 8,″3 Δ♌ 3′10,64 rückl. und hieraus ΔAp. = 19′ 43″ rechtl., Δ♌ = 9′ 22″,5 rückl.
- ↑ [640]
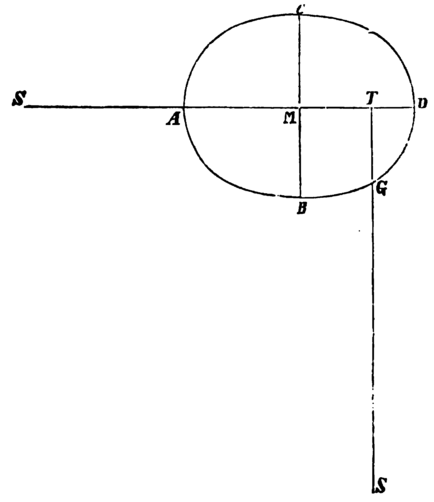
Fig. 264. No. 274. S. 444. Es sei ACDB die Mondbahn, T die Erde, A das Apogeum des Mondes, S die Sonne und deren Abstand von T im Mittel ST = a. Die halbe grosse Axe der Mondbahn sei AM = α, ihre halbe kleine MB = β, die Excentricität MT = αε, also AT = α(1 + ε) und SA = a — α(1 + ε). Ferner wird die Ordinate TG = α(1 - ε²) und SG = a — α(1 - ε²) also TG < AT, SG > AS. Wenn daher der Mond sich im Punkte A befindet, wird die Wirkung der Sonne auf ihn grösser sein, wenn die Sonne sich in der Richtung AD befindet, als die von S ausgehende Wirkung auf den in G befindlichen Mond, wenn die Sonne sich in der auf AD senkrechten Richtung TG befindet und zwar verhält sich die erste Anziehung zur zweiten wie .
Isaac Newton: Mathematische Principien der Naturlehre. Robert Oppenheim, Berlin 1872, Seite 444. Digitale Volltext-Ausgabe bei Wikisource, URL: https://de.wikisource.org/w/index.php?title=Seite:NewtonPrincipien.djvu/452&oldid=- (Version vom 12.5.2018)





