[1039] Zur Theorie der Strahlung bewegter Körper
von
Dr. Fritz Hasenöhrl.
(Mit 2 Textfiguren.)
(Vorgelegt in der Sitzung am 23. Juni 1904.)
Bewegt sich eine strahlende Fläche mit gleichförmiger Geschwindigkeit in derselben Richtung wie die von ihr ausgesandte Strahlung, so muß zur Überwindung des von letzterer ausgeübten Druckes beständig Arbeit geleistet werden. Diese Arbeit verwandelt sich nun gleichfalls in Strahlungsenergie, so daß also von einer in diesem Sinne bewegten Fläche um diesen Betrag mehr Energie ausgeht als von einer ruhenden. Bewegt sich hingegen die Fläche in der der ausgesandten Strahlung entgegengesetzten Richtung, so leistet letztere stets Arbeit und es geht dann von der bewegten Fläche um diesen Betrag weniger Energie aus als von einer ruhenden.
Bewegt sich andrerseits eine absorbierende Fläche so, daß sie vor der auffallenden Strahlung zurückweicht, so leistet letztere beständig Arbeit; die Fläche kann daher nur um das Äquivalent der letzteren weniger Strahlung absorbieren, d. h. in innern Wärmeinhalt verwandeln. Bewegt sich hingegen die absorbierende Fläche der auffallenden Strahlung entgegen, so muß beständig von außen Arbeit gegen den Druck der Strahlung geleistet werden. Diese Arbeit kann nur als Wärme in der absorbierenden Fläche auftreten. Die Wirkung der Bewegung ist also in diesem Falle die, daß die Fläche um den Betrag der geleisteten Arbeit mehr Wärme absorbiert.
[1040] Diese Auffassungsweise ist bereits von verschiedenen Autoren[1] ausgesprochen worden.
Im folgenden habe ich nun versucht, diese Sätze auf die Strahlung in einem bewegten Hohlraum anzuwenden. Außer der von den Wänden desselben gelieferten Strahlung muß sich in demselben auch Strahlungsenergie befinden, die aus mechanischer Arbeit gewonnen ist und wieder in solche verwandelt wird. Dieselbe ist wesentlich durch die Bewegung des Hohlraumes bedingt; ihr Betrag ist, wie sich zeigen wird, dem Quadrat der Geschwindigkeit des Systems proportional (in erster Annäherung), vermehrt also scheinbar die kinetische Energie des Systems. Es liegen also hier Verhältnisse vor, welche der Bewegung eines Elektrons ganz analog sind. Ebenso wie dort der Begriff »elektromagnetische Masse« eingeführt wird, könnte man auch hier von einer »scheinbaren Masse« sprechen, die durch die Strahlung bedingt ist. Ebenso wie die elektromagnetische Masse der statischen Energie des ruhenden Elektrons proportional ist, ist auch die durch Strahlung bedingte scheinbare Masse dem Energieinhalte des ruhenden Hohlraumes proportional. Und zwar ist der Proportionalitätsfaktor in beiden Fällen von derselben Größenordnung. Da nun der Wärmeinhalt jedes Körpers zum Teil aus Strahlungsenergie besteht, muß auch jeder Körper eine solche scheinbare, von der Temperatur abhängige Masse besitzen, die sich zu der Masse in gewöhnlichem Sinn addiert.
1.
Wir betrachten nun einen zylindrischen Hohlraum  , der sich mit konstanter Geschwindigkeit
, der sich mit konstanter Geschwindigkeit  in der Richtung des Pfeiles bewegt (Fig. 1). Sei
in der Richtung des Pfeiles bewegt (Fig. 1). Sei  die Geschwindigkeit des Lichtes und
die Geschwindigkeit des Lichtes und  . Ferner seien
. Ferner seien  und
und  zwei schwarze Flächen. Die Mantelfläche des Hohlraumes sowie die äußere Begrenzung der schwarzen Körper sei durch nach innen vollkommen
[1041] spiegelnde Flächen gebildet. Der Querschnitt des Raumes
zwei schwarze Flächen. Die Mantelfläche des Hohlraumes sowie die äußere Begrenzung der schwarzen Körper sei durch nach innen vollkommen
[1041] spiegelnde Flächen gebildet. Der Querschnitt des Raumes  sei gleich 1, seine Höhe gleich
sei gleich 1, seine Höhe gleich  . Der Außenraum sei ganz frei von Strahlung, also auf der absoluten Temperatur Null, während den Flächen
. Der Außenraum sei ganz frei von Strahlung, also auf der absoluten Temperatur Null, während den Flächen  und
und  eine bestimmte Temperatur zukommen soll.
eine bestimmte Temperatur zukommen soll.

Fig. 1.
Wir haben jetzt zwischen absoluter und relativer Strahlenrichtung zu unterscheiden;[2] es ist bequemer, unserer Betrachtung die letztere zu Grunde zu legen.
Sei nun

die Energiemenge, die  in der Zeiteinheit in der relativen Richtung zwischen
in der Zeiteinheit in der relativen Richtung zwischen  und
und  aussendet, wobei
aussendet, wobei  also der Winkel ist, den die relative Strahlenrichtung mit der Normalen (und mit der Richtung der Geschwindigkeit
also der Winkel ist, den die relative Strahlenrichtung mit der Normalen (und mit der Richtung der Geschwindigkeit  ) einschließt.
) einschließt.  muß dann (bezüglich
muß dann (bezüglich  ) eine Konstante sein, wie ich bereits in einer frühern Arbeit hervorgehoben habe.[3] Diese Strahlung übt nun auf
) eine Konstante sein, wie ich bereits in einer frühern Arbeit hervorgehoben habe.[3] Diese Strahlung übt nun auf  einen Druck aus, dessen in die Richtung der Normalen (im Sinne von
einen Druck aus, dessen in die Richtung der Normalen (im Sinne von  ) fallende Komponente den Wert
) fallende Komponente den Wert

haben möge. Multiplizieren wir diesen Ausdruck mit  , so erhalten wir die Arbeit, die in einer Sekunde von außen gegen diesen Druck geleistet wird, welche nun auch in Strahlung verwandelt wird, so daß also die gesamte Strahlung, welche
, so erhalten wir die Arbeit, die in einer Sekunde von außen gegen diesen Druck geleistet wird, welche nun auch in Strahlung verwandelt wird, so daß also die gesamte Strahlung, welche  in der gegebenen Richtung verläßt, den Wert
in der gegebenen Richtung verläßt, den Wert
[1042] 
hat. Dieser Ausdruck gibt uns nun auch den Betrag der in der Zeiteinheit auf  fallenden Strahlung an. Von derselben wird dort ein Teil absorbiert, ein Teil in Arbeit verwandelt. Falls
fallenden Strahlung an. Von derselben wird dort ein Teil absorbiert, ein Teil in Arbeit verwandelt. Falls  auf der absoluten Temperatur Null befindlich wäre, so wäre die eben betrachtete Strahlung die einzige in
auf der absoluten Temperatur Null befindlich wäre, so wäre die eben betrachtete Strahlung die einzige in  befindliche. Da in diesem Falle keine Widerstandskraft gegen die Bewegung unseres Systems zu erwarten ist, muß in
befindliche. Da in diesem Falle keine Widerstandskraft gegen die Bewegung unseres Systems zu erwarten ist, muß in  und
und  derselbe Druck nach entgegengesetzten Richtungen wirksam sein, so daß im ganzen keine Arbeit geleistet wird. Es wird also in
derselbe Druck nach entgegengesetzten Richtungen wirksam sein, so daß im ganzen keine Arbeit geleistet wird. Es wird also in  die Energiemenge
die Energiemenge

absorbiert und die Energiemenge

in mechanische Arbeit verwandelt.
Denken wir uns nun  auf derselben Temperatur wie
auf derselben Temperatur wie  befindlich, so gibt auch
befindlich, so gibt auch  in einer bestimmten Richtung die Energie
in einer bestimmten Richtung die Energie

ab. Übt diese Strahlung den Druck  aus, so leistet sie Arbeit, um deren Betrag die von
aus, so leistet sie Arbeit, um deren Betrag die von  gelieferte Energie zu vermindern ist, so daß also
gelieferte Energie zu vermindern ist, so daß also  von der Strahlungsmenge
von der Strahlungsmenge

verlassen wird. Dieselbe Energiemenge fällt in  auf und zwar lehrt eine der frühern ganz analoge Betrachtung, daß dortselbst die Energiemenge
auf und zwar lehrt eine der frühern ganz analoge Betrachtung, daß dortselbst die Energiemenge

absorbiert wird, weil gegen die auffallende Strahlung von außen die Arbeit  geleistet werden muß, die sich gleichfalls in Wärme verwandelt.
geleistet werden muß, die sich gleichfalls in Wärme verwandelt.
[1043] Es wird also von beiden Körpern  und
und  gleichviel absorbiert, wie emittiert; auf beiden Flächen lastet (in entgegengesetzter Richtung) derselbe Druck
gleichviel absorbiert, wie emittiert; auf beiden Flächen lastet (in entgegengesetzter Richtung) derselbe Druck

so daß in Summe keine Arbeit geleistet wird. Wenn also keine äußern Kräfte wirken, behält das System seine Geschwindigkeit bei.
Falls der eine der Körper  oder
oder  durch einen vollkommenen Spiegel ersetzt wird, muß der Strahlungszustand in
durch einen vollkommenen Spiegel ersetzt wird, muß der Strahlungszustand in  genau derselbe bleiben,[4] es ist also unter anderm dann auch
genau derselbe bleiben,[4] es ist also unter anderm dann auch  der Druck auf den Spiegel.
der Druck auf den Spiegel.
Wir fragen uns nun nach dem Energieinhalte des Raumes  . Die von
. Die von  nach
nach  gehende Strahlung hat die relative Geschwindigkeit:[5]
gehende Strahlung hat die relative Geschwindigkeit:[5]

Die von  nach
nach  gelangende Strahlung hat die Geschwindigkeit
gelangende Strahlung hat die Geschwindigkeit

beide haben den Weg  zurückzulegen, also ist der gesamte Energieinhalt des Raumes
zurückzulegen, also ist der gesamte Energieinhalt des Raumes 
![{\displaystyle {\overset {\pi /2}{\int _{0}}}{\frac {D}{\cos \phi }}\left[{\frac {2\pi (i_{0}+p_{1}c)\cos \phi \sin \phi \ d\phi }{{\mathfrak {B}}_{-}}}+{\frac {2\pi (i_{0}-p_{2}c)\cos \phi \sin \phi \ d\phi }{{\mathfrak {B}}_{+}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a45db9043be623145200b7bf40e9bda08335575)


|
(1)
|
Der erste der beiden Summanden gibt den Teil der Energie des Raumes  an, der von den schwarzen Körpern
[1044] geliefert wurde. Mit demselben hat sich meine bereits zitierte Arbeit beschäftigt.
an, der von den schwarzen Körpern
[1044] geliefert wurde. Mit demselben hat sich meine bereits zitierte Arbeit beschäftigt.
Der zweite Summand repräsentiert dagegen Strahlungsenergie, welche aus mechanischer Arbeit gewonnen ist. Da bei gleichförmiger Bewegung, wie wir sahen, keine Arbeit geleistet wird, muß dies eine Arbeit sein, welche bei Beschleunigung unseres Systems geleistet werden muß.
Man kann den Betrag dieser Energiemenge auch leicht auf folgende Weise bestimmen. Denken wir uns unser System in absoluter Ruhe, die beiden schwarzen Flächen  und
und  irgendwie am Ausstrahlen gehindert; den Raum
irgendwie am Ausstrahlen gehindert; den Raum  also ganz frei von Strahlung. Es soll nun in einem Augenblicke der Strahlung von
also ganz frei von Strahlung. Es soll nun in einem Augenblicke der Strahlung von  und
und  freie Bahn gelassen werden und gleichzeitig das System in verschwindend kurzer Zeit auf die Geschwindigkeit
freie Bahn gelassen werden und gleichzeitig das System in verschwindend kurzer Zeit auf die Geschwindigkeit  gebracht werden. Von diesem Augenblick an muß gegen die von
gebracht werden. Von diesem Augenblick an muß gegen die von  ausgehende Strahlung die Arbeit
ausgehende Strahlung die Arbeit  in der Zeiteinheit geleistet werden. Es vergeht nun die Zeit
in der Zeiteinheit geleistet werden. Es vergeht nun die Zeit  , bis diese Strahlung in
, bis diese Strahlung in  anlangt und dort ihrerseits das gleiche Arbeitsquantum liefert. Während dieser Zeit ist die von außen gelieferte Arbeit also unkompensiert. Ebenso leistet die von
anlangt und dort ihrerseits das gleiche Arbeitsquantum liefert. Während dieser Zeit ist die von außen gelieferte Arbeit also unkompensiert. Ebenso leistet die von  ausgehende Strahlung gleich von Beginn an die Arbeit
ausgehende Strahlung gleich von Beginn an die Arbeit  und es vergeht jetzt die Zeit
und es vergeht jetzt die Zeit  , bis diese Strahlung in
, bis diese Strahlung in  anlangt und dort die gleiche Arbeit im entgegengesetzten Sinne von außen her geleistet werden muß. Es wurde also von außen her um
anlangt und dort die gleiche Arbeit im entgegengesetzten Sinne von außen her geleistet werden muß. Es wurde also von außen her um

mehr Arbeit geleistet, als aus der Strahlung gewonnen. Integrieren wir diesen Betrag über alle Strahlungsrichtungen, so erhalten wir den obigen Ausdruck.
Falls unser System zu Anfang in Ruhe befindlich, die Flächen  und
und  jedoch nicht gehindert waren, Strahlung zu emittieren, befindet sich auch zu Anfang in
jedoch nicht gehindert waren, Strahlung zu emittieren, befindet sich auch zu Anfang in  Strahlungsenergie in bestimmtem Betrage. Die obige Überlegung deutet
[1045] an, daß diese Energie ganz absorbiert und nicht in Arbeit verwandelt wird. Und zwar läßt sich dies auch direkt zeigen, wenn man für
Strahlungsenergie in bestimmtem Betrage. Die obige Überlegung deutet
[1045] an, daß diese Energie ganz absorbiert und nicht in Arbeit verwandelt wird. Und zwar läßt sich dies auch direkt zeigen, wenn man für  und
und  ihre Werte einführt, die wir im folgenden Abschnitt angeben werden. Um den Gang der Untersuchung nicht zu unterbrechen, verlege ich den Beweis dieses Satzes in den § 4 dieser Abhandlung. Es ist also im Ausdruck (1) der erste Summand die von den strahlenden Körpern gelieferte Energie, der zweite die aus Arbeit entstandene. Wir bezeichnen letztere mit
ihre Werte einführt, die wir im folgenden Abschnitt angeben werden. Um den Gang der Untersuchung nicht zu unterbrechen, verlege ich den Beweis dieses Satzes in den § 4 dieser Abhandlung. Es ist also im Ausdruck (1) der erste Summand die von den strahlenden Körpern gelieferte Energie, der zweite die aus Arbeit entstandene. Wir bezeichnen letztere mit  , setzen also
, setzen also

|
(2)
|
2.
Wir wollen nun für die Größen  und
und  , die wir vorläufig unbestimmt ließen, ihren Wert einführen. Derselbe ist allgemein wohl zuerst von M. Abraham in seinen bereits zitierten Abhandlungen angegeben worden. Und zwar sind diese Werte aus der Lorentz’schen Theorie des Elektromagnetismus abgeleitet. Da man auch auf andrem Wege zu denselben Ausdrücken gelangt (siehe § 3 der vorliegenden Arbeit), erscheint ihre Richtigkeit noch wahrscheinlicher. Nach Abraham ist der Strahlungsdruck auf eine Fläche numerisch gleich der auffallenden oder ausgesandten Strahlung dividiert durch die Lichtgeschwindigkeit, und zwar wirkt dieser Druck in der absoluten Richtung der Strahlung. Sei
, die wir vorläufig unbestimmt ließen, ihren Wert einführen. Derselbe ist allgemein wohl zuerst von M. Abraham in seinen bereits zitierten Abhandlungen angegeben worden. Und zwar sind diese Werte aus der Lorentz’schen Theorie des Elektromagnetismus abgeleitet. Da man auch auf andrem Wege zu denselben Ausdrücken gelangt (siehe § 3 der vorliegenden Arbeit), erscheint ihre Richtigkeit noch wahrscheinlicher. Nach Abraham ist der Strahlungsdruck auf eine Fläche numerisch gleich der auffallenden oder ausgesandten Strahlung dividiert durch die Lichtgeschwindigkeit, und zwar wirkt dieser Druck in der absoluten Richtung der Strahlung. Sei  der Winkel, welchen die absolute Richtung der unter dem relativen Winkel
der Winkel, welchen die absolute Richtung der unter dem relativen Winkel  ausgesandten Strahlung mit der Richtung von
ausgesandten Strahlung mit der Richtung von  einschließt. Dann ist die früher mit
einschließt. Dann ist die früher mit  bezeichnete Größe
bezeichnete Größe

da wir ja unter  die – allein wirksame – normale Druckkomponente verstanden. Eine Beziehung zwischen
die – allein wirksame – normale Druckkomponente verstanden. Eine Beziehung zwischen  und
und  erhält man leicht aus nachstehender Figur 2, welche mit Fig. 1 meiner zitierten Abhandlung im wesentlichen identisch ist und welche wohl keiner weitem Erklärung bedarf.
erhält man leicht aus nachstehender Figur 2, welche mit Fig. 1 meiner zitierten Abhandlung im wesentlichen identisch ist und welche wohl keiner weitem Erklärung bedarf.
[1046] Es ist:


|
|
woraus sich die Beziehungen:

und

|
(3)
|
ergeben.
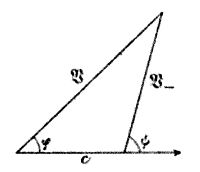
Fig. 2.
Es ist also:

|
(4)
|
setzen wir dies in die Gleichung  ein, so folgt
ein, so folgt

|
(5)
|
und


|
(6)
|
Ganz analog ergibt sich:

|
(7)
|
[1047] und

|
(8)
|
oder


|
(9)
|
Setzen wir dies in (2) ein, so wird:

![{\displaystyle \left[\cos \ \phi \left({\frac {1}{{\mathfrak {B}}_{-}}}-{\frac {1}{{\mathfrak {B}}_{+}}}\right)+\sigma {\sqrt {1-\sigma ^{2}\sin ^{2}\phi }}\left({\frac {1}{{\mathfrak {B}}_{-}}}+{\frac {1}{{\mathfrak {B}}_{+}}}\right)\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2efcc4a057507c4fa263a92d32bdaa8d9a86a5bb)

|
|
Setzen wir noch den Energieinhalt des ruhenden Hohlraumes 

so wird nach Durchführung der Integration
![{\displaystyle L=E_{0}{\frac {c^{2}}{{\mathfrak {B}}^{2}}}{\frac {1}{(1-\sigma ^{2})^{2}}}\left[{\frac {1}{2}}+{\frac {1}{2\sigma ^{2}}}-{\frac {(1-\sigma ^{2})^{2}}{4\sigma ^{3}}}\log {\frac {1+\sigma }{1-\sigma }}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7dbb536e9d251a4b5d5d64f805b32c459b71cd4)
Vernachlässigen wir hierin Größen von der Ordnung  , so wird
, so wird

Dieser Ausdruck hat nun die Form und die Dimension einer kinetischen Energie. Man kann also sagen, daß die kinetische Energie unseres Systems scheinbar um  vergrößert
[1048] wurde oder auch, daß zur mechanischen Masse unseres Systems noch eine scheinbare Masse
vergrößert
[1048] wurde oder auch, daß zur mechanischen Masse unseres Systems noch eine scheinbare Masse

hinzugekommen ist. Und zwar ist die Einführung dieser Masse ganz analog der der elektromagnetischen Masse. Bezeichnen wir für den Augenblick die Energie eines ruhenden Elektrons mit  , so ist die elektromagnetische Masse desselben gleich
, so ist die elektromagnetische Masse desselben gleich  oder
oder  ,[6] je nachdem man es mit Flächen- oder Volumenladung zu tun hat. Der Größenordnung nach ist also das Verhältnis dasselbe. Auch die exakten Ausdrücke haben eine gewisse Ähnlichkeit, da in beiden die Größe
,[6] je nachdem man es mit Flächen- oder Volumenladung zu tun hat. Der Größenordnung nach ist also das Verhältnis dasselbe. Auch die exakten Ausdrücke haben eine gewisse Ähnlichkeit, da in beiden die Größe  eine Rolle spielt.
eine Rolle spielt.
3.
In diesem Abschnitte möchte ich noch einige Bemerkungen über den Wert des Strahlungsdruckes machen.
Der gesamte Druck, der auf einer der Flächen  oder
oder  lastet, gleichgültig, ob dieselbe schwarz oder spiegelnd gedacht ist, hat den Wert
lastet, gleichgültig, ob dieselbe schwarz oder spiegelnd gedacht ist, hat den Wert

|
|
Wir wollen nun hierin die Dichte der Strahlung  einführen, welche etwa auf
einführen, welche etwa auf  fällt. Es ist
fällt. Es ist

(es ergibt sich dies aus (5)).
[1049] Es ist also

Wollen wir nun hierin wieder die absolute Strahlenrichtung einführen, so benützen wir die sich aus Fig. 2 sofort ergebende Relation

Und es wird

ein Ausdruck, der ebenfalls schon von Abraham[7] angegeben wurde.
Es läßt sich nun durch Verallgemeinerung eines Gedankens, den zuerst Larmor[8] ausgesprochen hat, dasselbe Resultat vom Standpunkt der elastischen Lichttheorie ableiten, was ich in Kürze hier zeigen möchte.
Wir betrachten eine Lichtwelle, welche sich unter dem (absoluten) Winkel  gegen die
gegen die  -Achse bewegt. Dieselbe ist gegeben durch
-Achse bewegt. Dieselbe ist gegeben durch

Fällt diese Welle auf einen Spiegel, der senkrecht zur  -Achse liegt, so bildet sich eine reflektierte Welle, die durch
-Achse liegt, so bildet sich eine reflektierte Welle, die durch

gegeben ist. Hierin ist  der Reflexionswinkel.
der Reflexionswinkel.
An der Oberfläche des Spiegels muß  sein. Bewegt sich derselbe mit der Geschwindigkeit
sein. Bewegt sich derselbe mit der Geschwindigkeit  in der Richtung seiner Normalen, also in der Richtung der positiven
in der Richtung seiner Normalen, also in der Richtung der positiven  -Achse, so muß also für
-Achse, so muß also für

sein.
[1050] Dies liefert
![{\displaystyle A\ cos\ m[t({\mathfrak {B}}+c\ \cos \ i)+y\ \sin \ i]+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64df6d059547a78b70842b8ea31b64c83e5df704)
![{\displaystyle +A'\cos \ m'[t(c\ \cos \ r-{\mathfrak {B}})-y\ \sin \ r]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebb9d66d5d0caed488072e8b075771ae1d25349b)
|
|
Diese Gleichung kann nur dann für alle Werte von  und
und  erfüllt sein, wenn
erfüllt sein, wenn

|
|
Diese Gleichungen liefern uns das Reflexionsgesetz

|
(10)
|
und den Dopplereffekt

in voller Übereinstimmung mit Abraham. Gleichung (10) ergibt sich übrigens auch leicht aus Gleichung (12) meiner frühern Abhandlung.[9]
Um nun daraus den Wert des Druckes abzuleiten, müssen wir annehmen, daß die Energiedichte einer Lichtwelle bei gleicher Amplitude der –2. Potenz der Wellenlänge, also der Größe  proportional ist. Wenn wir also mit
proportional ist. Wenn wir also mit  die Dichte der einfallenden Welle, mit
die Dichte der einfallenden Welle, mit  die der reflektierten bezeichnen, so ist
die der reflektierten bezeichnen, so ist

Nun ist die Energie, welche in der Zeiteinheit auf den Spiegel auffällt, im Raume  enthalten; die reflektierte Energie im Raume
enthalten; die reflektierte Energie im Raume  . Es ist also der Betrag der in einer Sekunde einfallenden Energie
. Es ist also der Betrag der in einer Sekunde einfallenden Energie

[1051] und der Betrag der in der gleichen Zeit reflektierten Energie

Die Differenz dieser beiden Ausdrücke muß der Arbeit des Strahlungsdruckes pro Zeiteinheit gleich sein. Es muß also

sein. Oder
![{\displaystyle cP={\mathfrak {B}}\rho (\cos \ i+\sigma )\left[\left({\frac {1+\sigma \cos \ i}{1-\sigma \cos \ r}}\right)^{2}{\frac {\cos \ r-\sigma }{\cos \ i+\sigma }}-1\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fc8d28c702f273a9feb2c78618d660bd6259763)
Mit Hilfe der leicht ableitbaren, bereits von Abraham gegebenen Beziehung:[10]

und der Gleichung:[11]

wird
![{\displaystyle cP={\mathfrak {B}}\rho (\cos \ i+\sigma )\left[{\frac {1+\sigma ^{2}+2\sigma \ \cos \ i}{1-\sigma ^{2}}}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1708b0db8eaeae89fdbbdb2b887b23f89976f02c)
und

Die Übereinstimmung mit dem von Abraham gegebenen Wert ist also eine vollständige ( hat hier das entgegengesetzte Vorzeichen wie früher).
hat hier das entgegengesetzte Vorzeichen wie früher).
Natürlich kann man auf dieser Grundlage auch die einzelnen Werte  und
und  berechnen, wenn man annimmt, daß ein bewegter Körper Wellen aussendet, deren Amplitude dieselbe ist, wie im ruhenden Zustande, während die Dichte der Strahlungsenergie dem Quadrate der Wellenlänge umgekehrt proportional ist.
berechnen, wenn man annimmt, daß ein bewegter Körper Wellen aussendet, deren Amplitude dieselbe ist, wie im ruhenden Zustande, während die Dichte der Strahlungsenergie dem Quadrate der Wellenlänge umgekehrt proportional ist.
[1052] Die Werte von  und
und  sind übrigens auch von Poynting[12] durch eine eigentümliche Betrachtung gewonnen worden. Allerdings beschränkt sich Poynting auf den Fall senkrechter Emission. Setzt man dementsprechend in die hier angegebenen Ausdrücke
sind übrigens auch von Poynting[12] durch eine eigentümliche Betrachtung gewonnen worden. Allerdings beschränkt sich Poynting auf den Fall senkrechter Emission. Setzt man dementsprechend in die hier angegebenen Ausdrücke  , so wird die Übereinstimmung vollständig.
, so wird die Übereinstimmung vollständig.
4.
Wir haben nun noch den Beweis der in § 1 gemachten Behauptung nachzutragen.
Unser durch Fig. 1 gegebenes System soll zu Beginn in Ruhe sein. Dann befindet sich im Raume  die Energiemenge
die Energiemenge

Es fragt sich nun, was mit dieser Energie geschieht, wenn das System plötzlich auf die Geschwindigkeit  gebracht wird. Von vornherein könnte man annehmen, daß nur ein Teil von ihr absorbiert wird, ein andrer Teil dagegen in mechanische Arbeit verwandelt wird.
gebracht wird. Von vornherein könnte man annehmen, daß nur ein Teil von ihr absorbiert wird, ein andrer Teil dagegen in mechanische Arbeit verwandelt wird.
Wir haben nun vor allem zu beachten, daß diese Energie nach den absoluten Richtungen gleichmäßig verteilt ist. Wenn wir also unsere frühere Bezeichnungsweise beibehalten, so ist die Dichte der Energie, deren absolute Fortpflanzungsrichtung mit der Normalen einen Winkel zwischen  und
und  einschließt,
einschließt,

Sobald das System in Bewegung ist, kommt es auf die Verteilung bezüglich der relativen Fortpflanzungsrichtung an. Dann ist offenbar die Dichte der Energie, deren relative Fortpflanzungsrichtung mit der Normalen einen Winkel zwischen  und
und  einschließt:
einschließt:

[1053] Dies wird durch Differentiation von Gleichung (3):


|
|
Da diese Energie in einem Zylinder von der Höhe  befindlich ist, ist die in dieser Richtung auf
befindlich ist, ist die in dieser Richtung auf  fallende Energiemenge gleich:
fallende Energiemenge gleich:

Wir sahen nun früher (§ 1), daß von der auffallenden Strahlung  der Teil
der Teil  absorbiert wird, während der Teil
absorbiert wird, während der Teil  in Arbeit verwandelt wird. Es wird also von der Einheit der auffallenden Energiemenge der Bruch
in Arbeit verwandelt wird. Es wird also von der Einheit der auffallenden Energiemenge der Bruch  absorbiert und der Bruchteil
absorbiert und der Bruchteil  in Arbeit verwandelt.
in Arbeit verwandelt.
Also wird von der jetzt auffallenden Energiemenge der Teil

absorbiert; der Teil

in Arbeit verwandelt.
Auf analoge Weise erkennt man, daß auf  die Energiemenge
die Energiemenge

auffällt und daß wir diese Energiemenge mit  , respektive mit
, respektive mit  zu multiplizieren haben, um die Teile derselben
[1054] zu erhalten, die absorbiert, respektive in Arbeit verwandelt werden.
zu multiplizieren haben, um die Teile derselben
[1054] zu erhalten, die absorbiert, respektive in Arbeit verwandelt werden.
Es wird also in Summe von den beiden Körpern die Energiemenge

absorbiert, während die Energiemenge

in Arbeit verwandelt wird. Und zwar kann man sich auch überzeugen, daß genau dieselben Ausdrücke gültig sind, wenn z. B. die schwarze Fläche  durch einen Spiegel ersetzt wird. Es wird nämlich dann die von
durch einen Spiegel ersetzt wird. Es wird nämlich dann die von  nach
nach  gelangende Strahlung in
gelangende Strahlung in  nicht absorbiert, sondern zum Teil reflektiert und zwar wird von der Einheit der in
nicht absorbiert, sondern zum Teil reflektiert und zwar wird von der Einheit der in  auffallenden Energie dann der Bruchteil
auffallenden Energie dann der Bruchteil  reflektiert; derselbe gelangt nach
reflektiert; derselbe gelangt nach  zurück und dort wird der Bruchteil
zurück und dort wird der Bruchteil  davon absorbiert, so daß endlich wieder der Bruchteil
davon absorbiert, so daß endlich wieder der Bruchteil  der sich anfangs in der Richtung von
der sich anfangs in der Richtung von  nach
nach  fortpflanzenden Strahlung absorbiert wird. Es bleibt also
fortpflanzenden Strahlung absorbiert wird. Es bleibt also  und daher auch
und daher auch  ungeändert.
ungeändert.
Benützt man nun die Gleichungen (4), (5), (7) und (8), so wird

und

![{\displaystyle \cdot \left[\sigma ^{2}\sin ^{2}\phi ({\mathfrak {B}}_{-}^{2}+{\mathfrak {B}}_{+}^{2})+\sigma \cos \phi {\sqrt {1-\sigma ^{2}\sin ^{2}\phi }}({\mathfrak {B}}_{-}^{2}-{\mathfrak {B}}_{+}^{2})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f129d6ca882108a2d93a536bc606d9f2fa9c713d)
|
|
[1055] Durch Ausführung dieser Integrationen überzeugt man sich nun, daß ganz exakt

ist.
Es wurde also die gesamte, ursprünglich in  vorhandene Energie absorbiert. Es werden also die frühern Behauptungen über die zur Beschleunigung notwendige Arbeit bestätigt. Andrerseits sehen wir auch ein, daß vom Energieinhalt eines bewegten Hohlraumes, also im Ausdruck (1) nur der erste Bestandteil vom Wärmeinhalt der strahlenden Körper geliefert wird. Es ist dies eine Annahme, von der ich in meiner zitierten Abhandlung über die Dimensionsveränderungen der Materie infolge ihrer Bewegung durch den Äther[13] ausgegangen bin und welche dort vielleicht nicht genügend begründet war.
vorhandene Energie absorbiert. Es werden also die frühern Behauptungen über die zur Beschleunigung notwendige Arbeit bestätigt. Andrerseits sehen wir auch ein, daß vom Energieinhalt eines bewegten Hohlraumes, also im Ausdruck (1) nur der erste Bestandteil vom Wärmeinhalt der strahlenden Körper geliefert wird. Es ist dies eine Annahme, von der ich in meiner zitierten Abhandlung über die Dimensionsveränderungen der Materie infolge ihrer Bewegung durch den Äther[13] ausgegangen bin und welche dort vielleicht nicht genügend begründet war.
- ↑ Siehe J. H. Poynting, Phil. Trans. 202, p. 525, 1904; Vl. v. Türin, Ann. d. Naturphil., III, p. 270, 1904; M. Abraham, Boltzmann-Festschrift, p. 84, und Drude, Ann. XIV, p. 236, 1904.
- ↑ Siehe darüber F. Hasenöhrl, diese Sitzungsber., CXIII., p. 469; – M. Abraham, l. c.
- ↑ L. c. p. 474.
- ↑ Vergl. J. Larmor, Boltzmann-Festschrift, p. 595, 1904.
- ↑ Vergl. F. Hasenöhrl, l. c.
- ↑ Siehe M. Abraham, Drude’s Ann., X, p. 151, 1903.
- ↑ Boltzmann-Festschrift, p. 91, Gl. 9.
- ↑ Larmor, Report of British Association, 1900.
- ↑ Diese Sitzungsber., CXIII, p. 489.
- ↑ L. c. Gl. 7c.
- ↑ Siehe F. Hasenöhrl, l. c. p. 489, Gl. 12.
- ↑ L. c. p. 551.
- ↑ L. c. p. 474, Fußnote.


























![{\displaystyle {\overset {\pi /2}{\int _{0}}}{\frac {D}{\cos \phi }}\left[{\frac {2\pi (i_{0}+p_{1}c)\cos \phi \sin \phi \ d\phi }{{\mathfrak {B}}_{-}}}+{\frac {2\pi (i_{0}-p_{2}c)\cos \phi \sin \phi \ d\phi }{{\mathfrak {B}}_{+}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a45db9043be623145200b7bf40e9bda08335575)




























![{\displaystyle \left[\cos \ \phi \left({\frac {1}{{\mathfrak {B}}_{-}}}-{\frac {1}{{\mathfrak {B}}_{+}}}\right)+\sigma {\sqrt {1-\sigma ^{2}\sin ^{2}\phi }}\left({\frac {1}{{\mathfrak {B}}_{-}}}+{\frac {1}{{\mathfrak {B}}_{+}}}\right)\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2efcc4a057507c4fa263a92d32bdaa8d9a86a5bb)


![{\displaystyle L=E_{0}{\frac {c^{2}}{{\mathfrak {B}}^{2}}}{\frac {1}{(1-\sigma ^{2})^{2}}}\left[{\frac {1}{2}}+{\frac {1}{2\sigma ^{2}}}-{\frac {(1-\sigma ^{2})^{2}}{4\sigma ^{3}}}\log {\frac {1+\sigma }{1-\sigma }}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7dbb536e9d251a4b5d5d64f805b32c459b71cd4)




















![{\displaystyle A\ cos\ m[t({\mathfrak {B}}+c\ \cos \ i)+y\ \sin \ i]+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64df6d059547a78b70842b8ea31b64c83e5df704)
![{\displaystyle +A'\cos \ m'[t(c\ \cos \ r-{\mathfrak {B}})-y\ \sin \ r]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebb9d66d5d0caed488072e8b075771ae1d25349b)













![{\displaystyle cP={\mathfrak {B}}\rho (\cos \ i+\sigma )\left[\left({\frac {1+\sigma \cos \ i}{1-\sigma \cos \ r}}\right)^{2}{\frac {\cos \ r-\sigma }{\cos \ i+\sigma }}-1\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fc8d28c702f273a9feb2c78618d660bd6259763)


![{\displaystyle cP={\mathfrak {B}}\rho (\cos \ i+\sigma )\left[{\frac {1+\sigma ^{2}+2\sigma \ \cos \ i}{1-\sigma ^{2}}}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1708b0db8eaeae89fdbbdb2b887b23f89976f02c)



























![{\displaystyle \cdot \left[\sigma ^{2}\sin ^{2}\phi ({\mathfrak {B}}_{-}^{2}+{\mathfrak {B}}_{+}^{2})+\sigma \cos \phi {\sqrt {1-\sigma ^{2}\sin ^{2}\phi }}({\mathfrak {B}}_{-}^{2}-{\mathfrak {B}}_{+}^{2})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f129d6ca882108a2d93a536bc606d9f2fa9c713d)
