Auszug aus den Anfangs-Gründen aller Mathematischen Wissenschaften/Die Hydraulick
Die Hydraulick ist eine Wissenschaft von der Bewegung des Wassers und anderer flüßigen Körper.
2. Durch eine Röhre verstehen wir einen jeden hohlen Cylinder.
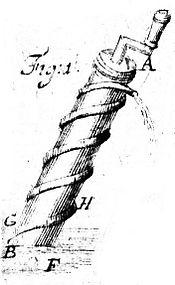
3. Das Wasser durch des Archimedis Wasserschraube in die Höhe zu bringen.[Fig. 1]
1. Um die Spindel AB windet eine bleyerne Röhre auf die Art und Weise, wie die Schraubengänge in einer Schraube (§. 90. Mech.) gemachet werden.
2. An die Spindel befestiget unten einen Zapfen, oben aber eine Kurbe, dabey ihr sie herumdrehen könnet.
3. Endlich leget die Schraube dergestalt, daß sie mit der Horizontallinie höchstens einen Winkel von 45° machet, und die untere Eröffnung unter dem Wasser stehet. So könnet ihr damit das Wasser heraufwinden.
Denn wenn die untere Eröffnung der Röhre [285] im Wasser stehet; so fället es durch seine Schwere hinein bis in F. Wendet ihr nun die Schraube um; so fället es von F bis G. Drehet ihr sie noch einmal herum; so fället es von G bis H u. s. w. bis es endlich oben in A herausfliesset. Also könnet ihr das Wasser bis in A hinaufbringen. W. Z. E.
Man kan durch Hülfe der Wasserschraube zwar mit geringer Kraft viel Wasser, jedoch nicht sehr hoch bringen. Daher wird sie im Grundbaue gebrauchet, wenn man das Wasser heraus haben will. Sie kan auch noch auf andere Art aus dünnen Brettern und Spänen gemachet werden, wie in den Anfangs-Gründen zu finden.

5. Durch ein Paternosterwerk das Wasser in die Höhe zu bringen.[Fig. 2]
1. Setzet eine hölzerne Röhre BL in das Wasser, die so hoch ist, als ihr das Wasser zu bringen gedenket.
2. Unter dem Wasser leget eine Welle ED mit ihren eisernen Zapfen auf ihr Lager.
3. Ueber die Röhre leget eine andere Welle GH gleichfalls auf ihr Zapfenlager.
4. Endlich nehmet ein Seil oder eine Kette mit ledernen Kugeln, die sich in die Röhre genau schicken, ziehet durch die Röhre und um beide Wellen, und bindet es zusammen.
Wenn ihr die obere Welle GH herumdrehet; so wird das Wasser bis in L gehoben werden. W. Z. T.
[286]Weil die Röhre unten in B ein wenig ausgeschnitten ist und im Wasser stehet; so muß das Wasser so hoch hineintreten, als die Röhre in dem Wasser stehet (§. 17. Hydrost.). Wenn ihr nun die obere Welle GH herumdrehet; so wendet sich die untere FD gleichfalls herum, und das Paternoster ziehet sich durch die Röhre BL. So bald nun eine Kugel in die Röhre kommet, lässet sie kein Wasser wieder heraus, und wenn sie in die Höhe gezogen wird, stösset sie es vor sich herauf und endlich oben in L heraus. W. Z. E.

6. Durch ein Schöpfwerk das Wasser in die Höhe zu bringen.[Fig. 3]
1. Leget wie vorhin ein sechseckigte Welle MN unter das Wasser, und oben, wo ihr das Wasser hin haben wollet, eine andere von gleicher Art und Grösse OP.
2. Bindet an zwey Seile oder Ketten Eimer S, und
3. hänget sie um die Wellen.
Wenn ihr die obere Welle OP herumdrehet; so werdet ihr mit den Eimern S das Wasser bis in P heben, und daselbst ausgiessen. W. Z. T.
Denn wenn ihr die Welle PO herumdrehet; so wendet sich die untere MN herum, und die Eimer S ziehen sich in die Höhe. Da nun die Eimer durch das Wasser gezogen werden, schöpfen sie [287] sich voll, und werden also voll heraufgebracht. Oben aber in P werden sie umgekehret, und giessen demnach das Wasser aus. W. Z. E.
7. Die Paternosterwerke sind kostbar zu unterhalten, weil die Kugeln sich leicht zerreiben, und nehmen auch viel Kraft weg, indem sie sich an der Röhre stark reiben. Die Schöpf-Werke sind im Winter nicht gut, weil die eisernen Ketten von der grossen Kälte springen. Seile hingegen zerreissen leicht.

8. Durch ein Schöpf-Rad das Wasser in die Höhe zu bringen.[Fig. 4]
1. Setzet ein Rad aus seinen Felgen und Schauffeln zusammen.
2. Zwischen zwey Schauffeln machet hin und wieder einen Kasten, der oben an der Stirne des Rades ganz zu ist, auf der einen Seite A aber ein paar Löcher hat, dadurch sich das Wasser einschöpfen kan.
3. Auf der einen Seite befestiget den Boden an den Felgen des Rades; auf der andern Seite aber lasset ihn über die Felge etwas vorgehen, damit ein geviertes Loch bleibe, dadurch das Wasser oben ausgeschüttet werden kan.
Wenn ihr dieses Rad ein wenig in das Wasser hänget, und es herumdrehet; so werden die Kasten Wasser schöpfen, indem sie durchgehen, und es oben wieder ausgiessen. Es werden die Schöpfräder auch noch auf viel andere Art gemachet.
[288]
9. Eine Plumpe zu machen, dadurch man das Wasser in die Höhe plumpen kan.[Fig. 5]
1. Setzet eine hölzerne Röhre ABDC ins Wasser.
2. Unten in den Boden DC machet eine Klappe oder Ventil I, welches sich zwar in die Höhe stossen, aber nicht herausdrücken lässet.
3. Befestiget an einer eisernen Stange EL den Plumpstock LK, der sich recht in die Röhre schicket, damit zwischen ihm und der Röhre kein Wasser durchkommen kan; mitten aber hohl ist.
4. Oben in L machet darein eine Klappe.
So werdet ihr das Wasser damit ausplumpen können.
Denn wenn ihr den Plumpstock KL in die Höhe ziehet; so ist in der Röhre ein leerer Raum, und wird von dem Drucken der Luft auf das umstehende Wasser die Klappe I aufgestossen, und das Wasser hineingetrieben (§. 27. Aerometr.). Stosset ihr den Plumpstock KL wieder zurücke; so schliesset sich die untere Klappe I zu, und die obere L thut sich auf: dadurch wird das Wasser über die Klappe L heraufgedruckt. Wenn ihr nun den Plumpstock von neuem in die Höhe hebet; so hebet ihr das Wasser zugleich mit herauf, bis es endlich an die Röhre MH kommet, und daselbst herauslaufet. W. Z. E.
[289]

10. Die schlechtesten Klappen C werden aus Leder gemachet, bekommen eine circulrunde Figur, und werden über das Loch im Boden, und im Plumpstocke auf der einen Seite angenagelt.[Fig. 6] Man machet sie ferner aus küpfernen Platten ED mit Gewinden, und überziehen sie mit dünnem Leder: befestiget daran eine Feder G, damit sie desto gewisser wieder zurück fallen.[Fig. 7]

11. Ein Druckwerk zu machen, dadurch man das Wasser sehr hoch drucken kan.[Fig. 8]
1. Machet zwey Stiefel ABCD aus Meßing, und unten im Boden CD ein Ventil.
2. Löthet an jeden eine Röhre an, die in H und I gleichfalls mit Ventilen versehen, so sich gegen N aufthun lassen.
3. Stosset einen Stempel K hinein, der sich genau in den Stiefel schicket, damit das Wasser zwischen ihm und der Röhre nicht heraufkommen kan.
Wenn ihr den Stempel K in die Höhe ziehet; so thut sich das Ventil im Bogen auf, und die äussere Luft treibet das Wasser in den Stiefel (§. 19. Aërom.). Stosset ihr ihn wieder zurücke; so schliesset sich das Ventil wieder zu, und das Wasser wird durch die Röhre zur Seiten herausgetrieben, welches das Ventil in I aufstösset, und ferner durch die in N angelöthete Röhre fortgestossen wird. Solchergestalt könnet ihr durch diese Maschine das Wasser in die Höhe drucken. W. Z. E.
[290]
12. Ein Ventil kan man auf folgende Art machen. Man höhlet den dicken Boden des Stiefels AC nach der Figur eines abgekürzeten Kegels aus, und schmergelt einen aus Meßing gegossenen abgekürzeten Kegel B hinein. Unten in D machet man einen Nagel vor, daß ihn das Wasser nicht umkehren kan, wenn sich das Ventil eröffnet. Man kan auch den Boden wie eine halbe Kugel aushöhlen, und eine Kugel von Meßing, die genau darein passet, hinein legen.[Fig. 9]
13. Es werden zwey Stiefel gemachet, damit die Maschine hurtig hinter einander das Wasser aussprützen kan, indem man es so anordnet, daß der eine Stempel niedergestossen wird, wenn man den andern in die Höhe ziehet. Man bedienet sich ihrer zu den Feuersprützen, ingleichen zu den Wasserkünsten.[Fig. 8]
14. Durch die Wasserkunst verstehen wir eine Maschine, dadurch das Wasser an alle umliegende Oerter, z. E. in die Brunnen aller Häuser durch die ganze Stadt, hingeleitet werden kan.
15. Eine Wasserkunst zu bauen.
1. Bauet einen Thurm, oder sonst ein Gebäude nach der Höhe der Oerter, wo das Wasser hingetrieben werden soll.
2. Leget darin ein Paternosterwerk (§. 5.), oder ein Schöpfwerk (§. 6.), oder ein Schöpfrad (§. 8.), oder ein Stangenwerk (§. 9.), oder auch ein Druckwerk (§. 11.) an: welches ihr entweder durch Wasser, oder durch Thiere, [291] oder durch Menschen bewegen könnet (§. 109. 110. 120. & seqq. Mech.). So könnet ihr das Wasser auf den Thurm hinaufbringen.
3. Oben sammlet das Wasser in einem Gefässe, an dessen Boden eine Röhre angemacht ist, dadurch es wieder herunter fallen kan.
4. Mit dieser Röhre verknüpfet unten andere, die unter der Erde horizontal, oder Berg an, bis an die Oerter geleget werden, wo man das Wasser hinleiten soll.
5. Endlich, wo das Wasser hingeleitet wird, richtet andere Röhren, so weit ihr wollet, wiederum bleyrecht auf, darein die Eröffnungen der ersteren gehen.
So wird das Wasser in diesen Röhren in die Höhe steigen (§. 15. Hydrost.): und demnach ist die Wasserkunst gebauet (§. 14.). W. Z. T. W.
16. Es ist wohlgethan, wenn man die Röhre in den Häusern fein weit wie einen Brunnen machet, und unten die Horizontal-Röhren mit einem Hahne versiehet, den man durch Hülfe einer langen eisernen Stange nach Gefallen auf- und zuschliessen kan. Denn so darf man nicht das Wasser beständig laufen lassen und kan im Winter die Röhre mit Mist und Stroh verbinden, daß das Wasser nicht gefrieret. Damit nun aber, wenn nur wenig Wasser verthan wird, der Kessel in der Wasserkunst nicht überlaufe, müsset ihr eine Röhre darein machen, dadurch es wieder zurücke in den Fluß laufen kan, wenn er zu voll wird.
17. Weil die Erfahrung lehret, daß das Wasser beynahe wieder so hoch steiget, als es gefallen ist; so könnet ihr Springbrunnen machen, wenn [292] ihr durch eine Wasserkunst das Wasser in die Höhe hebet, und aus dem Kessel durch Röhren zu dem Brunnen in kleine küpferne Röhren leitet, dadurch es springen soll.
18. Es solte vermöge der Hydrostatischen Gründe (§. 15. Hydrost.), das Wasser völlig so hoch steigen, als es heruntergefallen: allein die Erfahrung lehret das Widerspiel, indem es jederzeit etwas weniger in die Höhe steiget, als es gefallen ist; ja wenn die Röhre für den Druck zu weit ist, so springet es gar nicht, sondern laufet nur über. Diese Ursachen wollen wir hier nicht untersuchen.
19. Dem springenden Wasser allerhand Figuren zu geben.
Weil das Wasser im Springen die Figur der Eröffnung der Röhre annimmet, und ihre Richtung behält; so kommet hier alles auf die Figur und die Richtung der Eröffnung der Röhre an. Damit nun
1. Das Wasser wie ein Stab gerade in die Höhe springe; so richtet die Röhre auf der Horizontallinie perpendicular auf. Ist der Trieb stark, so könnet ihr eine hohle küpferne Kugel in das springende Wasser legen; so wird es dieselbe in die Höhe werfen. Weil sie nun nach einer Perpendicularlinie gegen die Horizontallinie zurücke fället; so kommet sie wieder in das Wasser, und wird von ihm von neuen in die Höhe getrieben. Solchergestalt spielet das Wasser mit der Kugel, als mit einem Balle.
[293] 2. Verlanget ihr, daß es zu allen Seiten ausgeworfen werde; so richtet eine Röhre perpendicular auf die Horizontallinie, andere machet selbst horizontal, noch andere lasset mit ihr einen schiefen Winkel machen. Oder könnet ihr auf die Röhre einen Aufsatz in Gestalt einer halben Kugel, oder eines oben verschlossenen Cylinders oder Kegels machen, welche rings herum mit subtilen Löchern durchstochen sind; so wird das Wasser allenthalben in subtilen Ströhmen herausspringen.
3. Wenn die Löchlein so subtil sind, daß kaum ein Haar durchkommen kan, und der Trieb stark genug ist; so formiret das Wasser einen Staubregen, welcher
4. angenehm lässet, wenn er durch die Peripherie einer strahlenden Sonne oder eines Sternes ausdunstet. Woraus ihr zugleich abnehmen könnet, wie das Wasser noch gar viele andere Figuren annehmen kan.
5. Endlich wenn ihr einen subtilen Ritz in dem Aufsatz machet, so wird das Wasser wie ein leinen Tuch sich ausbreiten.
Exempel von allen Aufsätzen findet man in Böcklers Architectura curiosa.

20. Ein Gießfaß zu machen, damit man den Garten begiessen kan.[Fig.10]
1. Machet eine Kugel, oder ein anderes Gefäß DB [294] von Blech, und durchstechet es im Boden mit subtilen Löchern.
2. Löthet eine Röhre an, deren Eröffnung E ihr mit dem Daumen verstopfen könnet.
Wenn ihr das Gefässe bis an die Röhre durch das Wasser stosset, und sie ist in E offen; so laufet es voll Wasser (§. 15. Hydrost.). Verstopfet ihr mit dem Daumen die Eröffnung E, und ziehet das Gefässe heraus; so kan kein Wasser durch die Löchlein herauslaufen, weil es die äussere Luft nicht herauslässet (§. 29. Aërom.). Thut ihr aber den Daumen weg; so drucket die Luft durch die Eröffnung E so viel auf das Wasser, als sie ihm unten und zu den Seiten bey den kleinen Löchern widerstehet. Dannenhero dringet es überall heraus. W. Z. E.

21. Hieraus erhellet zugleich, warum man mit dem Stechheber ACEDBF z. E. den Wein aus einem Fasse heben kan.[Fig. 11] Denn wenn er in F offen ist, und ihr stosset ihn durch das Spundloch in das Faß hinein; so trit in ihm durch E der Wein so hoch, als er im Weine stehet (§. 15. Hydrost.). Leget ihr auf F den Daumen, daß die Luft nicht hinein kan; so lässet auch die Luft unten durch E nichts herausfliessen. Also könnet ihr den Wein ausheben.

22. Wenn ihr den kurzen Theil AB eines Hebers ABC in das Wasser stecket, und durch [295] C die Luft aussauget: so muß das Wasser in dem kleinen Theile AB heraufsteigen, und durch den langen BC so lange herausfliessen, als die Eröffnung A unter dem Wasser, und die Eröffnung C niedriger als A stehet.[Fig.12]
Denn wenn ihr die Luft aus dem Heber ABC aussauget, so wird er leer. Da nun die Luft auf das Wasser drucket (§. 18. Aërom.), und ihr innerhalb dem Heber nichts widerstehet; so muß das Wasser in dem kleinen Theile AB von ihr hinaufgetrieben werden, welches hernach durch den grossen BC vermöge seiner eigenen Schwere herunter fället. Da nun aber die Luft in A so stark drucket als in C, hingegen weil BC höher ist, als AB, das Wasser in BC stärker gegen C, als das in AB gegen A, drucket (§. 17. Hydrost.); so muß das Wasser so lange durch C laufen, bis die Luft durch A in den Heber fahren und den ungleichen Druck aufheben kan (§. 13. Hydrost.). W. Z. E.
23. Es ist nichts daran gelegen, ob einer von beiden Theilen oder auch alle beide schlangenweise in die Krümme gebogen sind, oder nicht, wenn nur die untere Eröffnung C allezeit tiefer stehet, als die obere A (§. 17. Hydrost.).
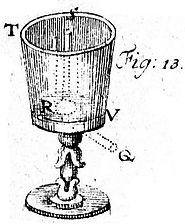
24. Man verändert zuweilen die Gestalt des Hebers, und machet anstatt des kurzen Theiles eine weite Röhre RS, die an den Boden eines Gefässes TV angelöthet ist und nur in R eine Eröffnung hat. Denn wenn das Wasser einmal durch die Röhre PQ zu fliessen anfänget, laufet es so lange, bis die Luft durch R in die weite Röhre RS kommen kan. Und dieser Heber wird Diabetes genennet.[Fig.13]
[296]25. Einen Brunnen zu machen, welcher eine Weile Wasser giebet, über eine Weile zu fliessen aufhöret, und über eine Weile wiederum zu fliessen anfänget.[Fig. 14]

1. Löthet in ein rundes Gefäß AB, so unten rings herum verschiedene kleine Löcher hat, eine Röhre FHM, die unten und oben offen ist, und fast bis an den Deckel des Gefässes L gehet.
2. Löthet das untere Ende der Röhre an eine Schaale CD, daraus durch ein kleines Löchlein in der Mitten das Wasser in ein darunter gesetztes oder befestigtes Gefässe abfliessen kan. Doch muß die Röhre bey dem Löchlein eine Eröffnung M zur Seite behalten.
Wenn nun das obere Gefässe mit Wasser gefüllet wird, so laufet es durch die kleinen Löchlein herab in die Schaale, und versetzet die Eröffnung der Röhre M, daß keine Luft hineinkommen kan. Derowegen muß das Wasser aufhören herabzufliessen. Unterdessen fliesset es aus der Schaale durch das Löchlein in das untere Gefässe, und so bald die untere Eröffnung der Röhre M wieder frey wird, daß die Luft dadurch in das obere Gefässe hinein kan, laufet[WS 1] das Wasser oben von neuem heraus.
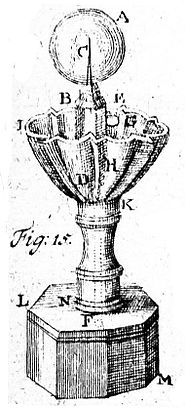
26. Einen Springbrunnen zu machen, darinnen das Wasser durch eine Röhre aus einem niedrigen Gefässe in eine gläserne Kugel springet.[Fig. 15]
[297]1. An eine grosse gläserne Kugel A machet eine breite Schraube BE.
2. Daran befestiget die Röhre CD, welche oben in C sehr enge, unten aber in D weiter ist; ingleichen eine andere EF, die oben an der Schraube in E weit, hingegen unten in F enge und beynahe zweymal so lang, als DC ist.
3. An den Boden des Gefässes IK ist eine Röhre GH angelöthet, damit aus demselben kein Wasser in das untere Gefäß LM laufen kan.
4. Füllet bis an G das Gefässe IK mit Wasser, imgleichen ohngefehr den dritten Theil der Kugel A.
Wenn ihr die Röhre EF durch die Röhre GH stecket, und die Röhre DC, so unten an das Gefässe befestiget worden, in dem Wasser stehet; so wird das Wasser aus der Kugel durch die Röhre EF herunter fallen, und aus dem Gefässe IK durch die Röhre DC in die Kugel springen.
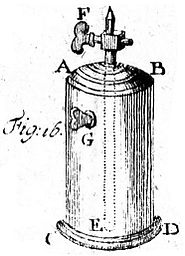
27. Durch die zusammengedruckte Luft das Wasser springend zu machen.[Fig. 16]
1. Machet ein rundes Gefässe aus starkem Kupfer AD, oben und unten mit einem dicken Boden von Meßing.
2. In dem unteren Boden CD machet ein Loch mit einer Schraube, dadurch ihr das Gefässe mit Wasser füllen könnet.
3. An den oberen Boden AB löthet die Röhre EF, [298] welche beynahe bis an den unteren Boden reichet, und oben ausser dem Gefässe AD mit Schraubengängen versehen ist, damit sie nicht allein an die Luftpumpe, sondern auch auf die Fontaine an die Aufsätze angeschraubet werden könne.
Wenn ihr nun die Luft in dem Gefässe AD durch die Luftpumpe oder eine Sprütze zusammendrucket (§. 41. Aërom.), und, nachdem ihr sie wieder ab- und einen Aufsatz angeschraubet, den Hahn aufmachet; so wird die Luft das Wasser durch F mit Gewalt herausjagen.
Denn indem die Luft zusammengedruckt wird, so wird ihre ausdehnende Kraft verstärket (§. 24. Aërom.). Da sie nun stärker drucket, als die äussere in F widerstehet; so muß sie das Wasser durch die Röhre EF herausjagen, bis sie mit der äusseren wieder in wagerechten Stand gesetzet wird (§. 13. Hydrost.). W. Z. E.

Küttet in ein Glas AB eine gläserne Röhre CD, die oben eine sehr subtile Eröffnung hat, und beynahe bis an den Boden des Glases D gehet. Wenn ihr das Glas mit Wasser, doch nicht ganz voll, füllet, und durch die Röhre hineinblaset; so wird, wenn ihr zu blasen aufhöret, das Wasser zu springen anfangen.[Fig. 19]
Der Beweis ist eben wie vorhin.
28. Wenn ihr diese Fontaine füllen wollet, so dürfet ihr nur [299] die Luft durch die Röhre ansaugen, und die Eröffnung behende in das Wasser stecken; so wird die äussere Luft beynahe so viel Wasser hineindrucken, als Luft herauskommet (§. 34. Aërom.).
29. Einen Springbrunnen zu machen, darinnen das herausspringende Wasser das andere nach sich heraustreibet.[Fig. 17]

1. Nehmet zwey Gefässe PR und HQ, deren jedes auf allen Seiten feste zu ist, und setzet sie entweder auf einander, oder eines über das andere, nachdem es euch bequem fället.
2. An den Deckel des obern Gefässes PD, der wie eine Schüssel oder Schale vertiefet worden, löthet eine Röhre DL, die oben und unten offen ist, und beynahe den Boden des unteren Gefässes erreichet.
3. An den Deckel des unteren Gefässes HR löthet eine Röhre FM, die gleichfalls beiderseits offen, und beynahe den Deckel des oberen Gefässes PD erreichet.
4. Endlich löthet mitten an den Deckel des oberen Gefässes die Röhre AC, so beynahe bis an seinen Boden HR gehet, und oben eine ganz subtile Eröffnung A hat.
Wenn ihr das obere Gefässe PR mit Wasser füllet, und anfangs in die Schüssel KO etwas giesset; so wird das Wasser aus dem Gefässe zu springen anfangen, und so lange fortspringen, als etwas in demselben übrig ist.
Denn wenn das Wasser aus der Schüssel KO [300] durch die Röhre DL hinunter fället, jaget es die Luft aus dem Gefässe HQ durch die Röhre FM in das obere Gefässe. Da sie nun etwas zusammengedrucket wird, so wird ihre ausdehnende Kraft vermehret (§. 24. Aërom.). Derowegen weil die äussere Luft bey A weniger Widerstand thut, als die innere auf das Wasser in dem Gefässe PR drucket; so muß das Wasser durch die Röhre CA hinausgetrieben werden. Da nun das herausgetriebene Wasser in der Schüssel KO aufgesammlet wird; fliesset es beständig durch die Röhre DL hinunter, und jaget die Luft aus dem unteren Gefässe HQ durch die Röhre FM in das obere PR. Derowegen springet es so lange, als Wasser in dem Gefässe PR ist. Und solchergestalt jaget das Wasser, was herausspringet, das andere nach sich heraus. W. Z. E.
30. Diesen anmuthigen Brunnen hat Heron von Alexandrien erfunden, daher er auch billig zu seinem Andenken der Herons-Brunnen (Fons Heronis) genennet wird. Es springet aber das Wasser aus eben dem Grunde, wie in dem vorhergehenden (§. 27.), nur daß hier die Luft auf eine besondere Art, nemlich durch die Schwere des Wassers in die Röhre DL zusammengedruckt wird.
31. Einen Springbrunnen zu machen, darinnen das Wasser durch die Wärme zum Springen gebracht wird.[Fig. 18]

1. Setzet zwey Gefässe AD und DE, wie in der vorhergehenden Aufgabe, entweder unmittelbar [301] auf einander, oder sonst nach Gelegenheit auch nur über, ja gar neben einander.
2. An den Deckel des unteren Gefässes CF (oder wie es sonst die Gelegenheit leidet) löthet eine Röhre KI, die beynahe den Deckel des anderen Gefässes AB erreichet.
3. Mitten an diesem Deckel AB löthet die Röhre ML, dadurch das Wasser springen soll, und
4. Endlich machet oben ein Gefässe GB, darinnen das herausspringende Wasser gesammlet werden kan.
Wenn ihr unter das Gefässe CF glüende Kohlen setzet, oder sonst ein Feuer machet: so wird das Wasser in M herausspringen.
Denn durch die Wärme wird die ausdehnende Kraft der Luft in dem Gefässe CF gewaltig vermehret (§. 45. Aërom.). Da sie nun durch die Röhre IK stärker auf das Wasser in dem Gefässe AD, als die äussere Luft durch die Röhre LM drucket; so wird das Wasser durch gedachte Röhre hinausgetrieben.
Anmerkungen (Wikisource)
- ↑ Vorlage: lauet
