Auszug aus den Anfangs-Gründen aller Mathematischen Wissenschaften/Die Optick
Die Optick ist eine Wissenschaft aller sichtbaren Dinge, in so weit sie durch Strahlen, die von ihnen gerades Weges in das Auge fallen, sichtbar sind.
2. Unterweilen verstehet man durch die Optick eine Wissenschaft aller sichtbaren Dinge, in so weit sie sichtbar sind, und begreifet die Catoptrick und Dioptrick mit darunter.
3. Dasjenige, welches alle Dinge um uns sichtbar machet, nennen wir das Licht, den Mangel des Lichts aber Schatten, und die Abwesenheit alles Lichtes Finsterniß.
4. Ohne Licht kan nichts gesehen werden (§. 3.).
5. Je mehr der Zufluß des Lichts an einem Orte gehindert wird, je stärker ist der Schatten.
6. Lasset durch ein kleines Löchlein, in der Grösse einer Linse, das Licht der Sonnen in einen verfinsterten Ort hineinfallen; so werdet [303] ihr wahrnehmen, daß ein heller Strahl in einer geraden Linie fortgehet.
7. Derowegen kan man die Strahlen des Lichts durch gerade Linien vorstellen.
8. Da nun das Licht nach geraden Linien fortgehet; so können wir nichts sehen, was nicht mit dem Auge in einer geraden Linie lieget, es sey denn daß der Strahl unterweges aus seinem Wege gebracht wird (§. 10. 14.).

9. Wenn also viele Strahlen Ab, Ac, Ad, Ae, Af aus einem Puncte A fliessen; so gehen sie immer weiter von einander, je weiter sie kommen, und daher wird das Licht immer schwächer.[Fig. 1]

10. Wenn ihr den Strahl, so in den verfinsterten Ort hineinfället GC, mit einem Spiegel BD dergestalt auffanget, daß er mit ihm einen rechten Winkel GCD machet; so prallet er in sich selbst zurücke. Hingegen wenn ihr den Spiegel BD so haltet, daß der einfallende Strahl FC mit ihm einen schiefen Winkel FCD machet: so prallet er auf der anderen Seite zurücke, und machet der zurückprallende Strahl EC eben so einen grossen Winkel ECB mit dem Spiegel, als der einfallende.[Fig.2]
[304]11. Dieses Zurückprallen der Strahlen wird die Reflexion genennet. Der Winkel FCD, den der einfallende Strahl FC mit dem Spiegel BCD machet, heisset der Einfalls-Winkel (Angelus incidentiae). Der Winkel ECB aber, den der zurückgeworfene Strahl EC mit dem Spiegel machet, der Reflexions-Winkel (Angelus reflexionis).[Fig. 2]
12. Daher ist in einem Spiegel der Reflexionswinkel ECB dem Einfallswinkel FCD gleich (§. 10).[Fig. 2]

13. Füllet ein Conisches Glas HKI mit Wasser, und lasset den Strahl LM in dem verfinsterten Orte schief darauf fallen; so wird er nicht in einer geraden Linie in N hinfahren, sondern, wenn er aus dem Glase wieder in die Luft kommet, nach der Linie MO fortgehen, nicht anders, als wenn der aus P kommen wäre.[Fig. 3]
14. Wenn also der Strahl des Lichtes aus einer dichteren Materie in eine dünnere, oder aus einer dünneren in eine dichtere fähret; so wird er gebrochen.
15. Dieses Brechen der Strahlen, das ist, ihre Abweichung von der vorigen Linie, in welcher sie waren, wird die Refraction genennet.
[305]
16. Der Winkel VSX, den der einfallende Strahl TV mit dem gebrochenen SX machet, heisset der Refractions-Winkel (Angulus refractionis). Der Winkel ZSX, den der gebrochene Strahl SX mit der Linie SZ machet, welche in dem Einfallspuncte S auf der Fläche des Körpers QR, darauf der Strahl fället, perpendicular stehet, wird der gebrochene oder refringirte Winkel (Angulus refractus) genennet. Endlich der Winkel TSY, den der einfallende Strahl TS mit gedachter Perpendicularlinie SY machet, bekommet den Namen des Neigungswinkels oder Inclinationswinkels (Angulus inclinationis.).[Fig. 4]

17. Ein einiger Punct einer Sache A kan an allen Orten b. c. d. e. f. gesehen werden, wohin man aus ihm eine gerade Linie ziehen kan.[Fig. 1]
18. Also wirft jeder Punct einer jeden Sache unzählig viel Stahlen um sich aus (§. 3.).
19. Das Auge bestehet aus verschiedenen Häuten und Feuchtigkeiten. Die erste Haut ist wie ein durchsichtiges Horn, und wird daher die Hornhaut (Cornea) genennet. Mit ihr ist an dem hinteren und grösten Theile des [306] Auges eine andere zähe Haut (Sclerotica) verknüpfet, die wir die harte Haut nennen wollen. Unter der Hornhaut ist eine farbigte Haut (Uvea), deren Farben von den Unwissenden der Hornhaut beygeleget werden. Diese hat mitten ein circulrundes Loch (Pupilla), welches wir den Stern nennen wollen. Mit der farbigen Haut ist eine schwarze (Choroides) verknüpfet, welche an der harten anlieget. Endlich über die schwarze ist hinten an dem Auge ein zartes netzförmiges Häutlein(Retina), welches wie ein Rotz zusammenfället, wenn man es absondert, hingegen sich wie ein leinenes Tuch ausspannet, wenn es innerhalb dem Wasser beweget wird. Es ist aus subtilen Nerveu gewebet. Den hintersten und grösten Theil des Auges füllet die gläserne Feuchtigkeit (humor vitreus) aus, welche einer aus Kraftmehle zubereiteten Stärke gleichet. Mitten in dem Auge unter dem Sterne lieget die crystalline Feuchtigkeit (humor crystallinus) die einem geschliffenen Glase ähnlichet, und beiderseits eine Rundung hat. Endlich den Raum zwischen der crystallinen Feuchtigkeit und der Hornhaut, erfüllet eine wässerige Feuchtigkeit (humor aqueus), die bald herausfliesset, wenn die Hornhaut verletzet wird.
20. Haltet die crystalline Feuchtigkeit vor ein angezündetes Licht, oder gegen ein Fenster, [307] und darhinter ein Papier. Rücket mit dem Papiere nach und nach gegen jene zu; so werdet ihr das Licht mit der Bewegung der Flamme; imgleichen das Fenster mit seinen Glasscheiben, sehr subtil darauf abgebildet sehen, jedoch umgekehret, so daß die Spitze der Flamme gegen den Erdboden stehet. Ziehet die crystalline Feuchtigkeit von dem Lichte etwas weiter weg; so wird das Bildlein auf dem Papiere verschwinden, aber wiederkommen, wiewohl etwas kleiner, wenn ihr mit dem Papiere näher hinzurücket. Eben dieses geschiehet mit einem erhabenen geschliffenen Glase.
21. Die Körper, von welchen Strahlen in das Auge fallen, mahlen sich sehr nett und subtil, aber umgekehret, hinter der crystallinen Feuchtigkeit ab.
22. Dieses Bildlein ist näher hinter ihr und kleiner, wenn die abgebildete Sache weit weg ist, als wenn sie nahe ist.
23. Da nun die nahen Sachen groß, die weiten klein aussehen; so siehet eine Sache groß aus, wenn in dem Auge ein grosses Bild abgemahlet wird, hingegen klein, wenn sich ein kleines abmahlet. Und daher müssen zwey Körper gleich groß aussehen; wenn ihre Bilder im Auge gleich groß seyn.
[308]24. Wenn die Sache beweget wird, so beweget sich auch das Bild im Auge. Daher sehen wir die Sache in der Bewegung, wenn das Bildlein in dem Auge nicht auf einer Stelle stehen bleibet.
25. Weil das Bildlein gar sehr viel kleiner ist, als die Sache, die es abbildet; so kan entweder wegen der Kleinigkeit der Sache, oder der allzugrossen Weite von dem Auge, das Bildlein so klein werden, daß es einen untheilbaren Punct im Auge einnimmet, und also die Sache nicht mehr abbildet. Derowegen kan in diesem Falle die Sache nicht gesehen werden.
26. Weil nun keine Sache in der Nähe ist, da nicht einige Theilchen; hingegen auch keine in der Weite, da nicht einige grosse Theile unsichtbar seyn solten; so kan man weder jene, noch diese mit blossen Augen ganz deutlich sehen, wiewohl jene deutlicher, als diese. Denn wir sehen etwas deutlich, wenn wir alle Theile unterscheiden können, die in der That von einander unterschieden sind.
27. Weil das Bildlein sich auf dem netzförmigen Häutlein darstellet: so muß die crystalline Feuchtigkeit ihm näher seyn, wenn ihr in der Ferne etwas deutlich sehet, als wenn ihr in der Nähe etwas erkennet (§. 22.).
[309]
28. Daher muß in einem Auge, welches sowohl in die Ferne, als in die Nähe siehet, die crystalline Feuchtigkeit ihre Entfernung von dem netzförmigen Häutlein verändern können.
29. Wenn die crystalline Feuchtigkeit dem netzförmigen Häutlein zu nahe ist, so können sich die nahen Sachen nicht deutlich auf ihm abbilden. Ist sie aber von ihm zu weit weg, so kan von den weiten kein deutliches Bild auf ihm formiret werden (§. 22.). Derowegen kan man in dem ersten Falle nicht wohl in die Nähe, in dem andern nicht wohl in die Ferne sehen.
30. Alle Veränderungen, die in dem Auge vorgehen, kan man auch in einem verfinsterten Zimmer wahrnehmen, wenn man durch ein geschliffenes, auf einer Seite kugelrundes, auf der anderen aber ebenes, oder auch auf beiden Seiten kugelrundes Glas (welches mit der crystallinen Feuchtigkeit im Auge übereinkommet) das Licht hineinfallen lässet. Denn es mahlen sich in einer gewissen Weite von dem Glase alle Sachen, von denen Strahlen auf das Glas fallen können, umgekehret auf das allerdeutlichste mit ihren Farben und Bewegungen ab. Dergleichen verfinsterten Ort pflegt man eine Cameram obscuram zu nennen. Wenn das Löchlein nicht viel grösser als eine Linse oder Erbse ist; kan das geschliffene Glas wegbleiben. Denn weil alsdenn die Strahlen des Lichtes, die von verschiedenen Puncten der Fläche eines Körpers hineinfallen, alle auf besondere Puncte der Wand fallen, und ohne Vermengung in das Auge zuückgeworfen werden: so müssen sie noch eben die Kraft behalten, die sie vorher hatten, nemlich die strahlenden Puncte, von denen sie ausgestossen, vorzustellen.
[310]
31. Leget den Spiegel an das Fenster, und tretet vor denselben. Nehmet wahr, wie groß der Stern im Auge ist. Haltet beide Hände an die Schläfe, daß von der Seiten kein Licht mehr in die Augen fallen kan; so werdet ihr sehen, daß der Stern merklich grösser wird. So bald ihr aber die Hände zurückziehet, wird auch der Stern sich wieder zusammenziehen.
32. Der Stern im Auge wird grösser, wenn das Licht abnimmet; hingegen kleiner, wenn das Licht zunimmet.
33. Dannenhero ist er in der hellen Mittagssonne überaus klein; in der Abenddemmerung sehr groß.
34. Wenn das Licht auf einen dunkelen Körper fället; so wirft er allezeit einen Schatten hinter sich, dem Lichte gegen über.
Denn der dunkele Körper lässet keine Strahlen des Lichtes durchfallen. Da sie nun in einer geraden Linie fortgehen (§. 6.); so hindert er, daß auf einen gewissen Raum hinter ihm Strahlen fallen können. Und daher ist hinter dem Körper, dem Lichte gegen über, ein Schatten (§. 3). W. Z. E.
[311]35. Wenn derowegen das Licht seine Stelle verändert, so rücket auch der Schatten aus seiner Stelle fort. Eben dieses muß geschehen, wenn der erleuchtete Körper sich beweget. Und dannenhero scheinet es in beiden Fällen, als ob sich der Schatten bewegete.
36. Weil nichts ohne Licht gesehen werden kan (§ 4.); der Schatten aber ein Mangel des Lichtes ist (§. 3.); so kan er nur gesehen werden, in so weit der Körper, der im Schatten lieget, einiges zurückfallendes Licht von der Seiten her empfänget, und in so weit man die Gränzen des Schattens und Lichtes sehen kan.

37. Aus der gegebenen Höhe eines Körpers TS, und der Höhe der Sonne über dem Horizont SVT, die Länge des Schattens TV zu finden.[Fig. 7]
Weil in dem rechtwinkelichten Triangel STV der Winkel V gegeben ist, als der das Maaß der Sonnen-Höhe ist; so wisset ihr auch den dritten S (§. 77. Geom.). Derowegen könnet ihr die Länge des Schattens TV (§. 20. Trigon.) finden. W. Z. T. u. Z. E.
Es sey die Sonnen-Höhe SVT 37° 45’, TS 187 Schuhe.
[312]
| Log. Sin. V | 9.7869056 | |
| Log. TS | 2.2718416 | |
| Log. Sin. S | 9.8980060 | |
| _________________________ | ||
| 1.2.1.69.8476 | ||
| _________________________ | ||
| Log. TV | 23829420 | welchen in den Tabellen am nächsten kommet 2415’’. |
38. Wenn euch die Höhe TS und die Länge des Schattens TV gegeben wird; so könnet ihr (§. 26. Trigon.) die Sonnen-Höhe TVS finden.
39. Wenn ihr den Schatten TZ kürzer annehmet als TV; so ist der Winkel TZS den beiden Winkeln ZVS und ZSV zusammmen gleich (§. 74. Geom.). Und demnach ist der Schatten eines Körpers kürzer, wenn die Sonne (oder ein anderes Licht) hoch, als wenn sie niedrig stehet.
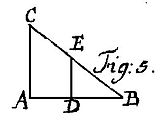
40. Aus der gegebenen Länge des Schattens zweyer Körper AB und DB und der Höhe des einen DE, die Höhe des andern zu finden.[Fig. 5]
Wenn der Körper DE dergestalt hinter dem Körper AC stehet, daß beider Schatten in B aufhöret; so ist wegen der rechten Winkel bey D und A die Linie DE mit AC parallel (§. 73. Geom.), folgends: wie der kurze Schatten DB zu der kleinen Höhe DE, so der lange Schatten [313] AB zu der grossen Höhe AC (§. 149. Geom.). Derowegen könnet ihr diese durch die Regel Detri finden.
41. Weil die Sonne von der Erde so weit weg ist, daß die ganze Breite der Erde in Ansehung ihrer Entfernung nur für eine Linie zu halten, wie in der Astronomie erwiesen werden soll; so bleibet der Winkel B in einer Grösse, wenn DE nicht auf besagte Weise hinter dem Körper AC, sondern in einem jeden andern Orte stehet.
42. Derowegen wenn ihr auf dem Felde einen Stock DE nach Belieben einstecket, seine Höhe und die Länge seines Schattens DB messet, über dieses die Länge des Schattens eines Baumes, oder Thurmes, oder einer andern Höhe AB erforschet; so könnet ihr nach gegenwärtiger Aufgabe dieselbe Höhe finden.
| Es sey DB | 7’ | DE | 5’ | AB 45’. |
| 7 — 5 | — | 45 | ||
| 5 | ||||
| 225 | ||||
11 | 225| 32 AC. 77|
43. Wenn der dunkele Körper kleiner ist, als das Licht; so wird der Schatten immer schmäler, je weiter er vom Körper wegkommet. Ist er grösser; so wird der Schatten immer breiter. Wenn aber beide Körper von gleicher Grösse sind; so behält der Schatten überall Eine Breite.
[314]
Die Axe gehet mitten durch das Licht und den erleuchteten Körper, und der äussere Strahl berühret sowohl das Licht, als den erleuchteten Körper. Wenn nun das Licht grösser ist, als dieser; so ist der Strahl in diesem der Axe näher, als in jenem. Derowegen kommet der Schatten hinter dem Körper der Axe immer näher, je weiter er von ihm weg ist. Welches das erste war.
Hingegen wenn das Licht kleiner ist, als der erleuchtete Körper; so ist der äussere Strahl in jenem der Axe näher, als in diesem, und dannenhero gehet der Schatten immer weiter von der Axe weg, je weiter er von dem Körper wegkommet. Welches das andere war.
Wenn die beiden Körper von gleicher Grösse sind, so sind die beiden äussersten Strahen parallel. Derowegen bleibet der Schatten beständig von Einer Breite (§. 22. Geom.). Welches das dritte war.
44. Wenn das Licht und der erleuchtete Körper Kugeln von gleicher Grösse sind; so ist der Schatten cylindrisch. Wenn das Licht eine grössere Kugel ist, als der erleuchtete Körper; so hat der Schatten die Figur eines Kegels. Endlich wenn das Licht eine kleinere Kugel ist, als der erleuchtete Körper; so hat der Schatten die Figur eines Bechers.
[315]Die äussersten Strahlen berühren ringsherum den erleuchteten Körper. Derowegen wenn dieser eine Kugel ist; so ist die Grundfläche des Schattens ein Circul. Da nun in dem ersten Falle der Schatten einerley Breite behält, in dem andern aber immer schmäler, und in dem dritten immer breiter wird; so muß die Figur im ersten ein Cylinder (§. 179. Geom.), im andern ein Kegel (§. 185. Geom), und im dritten ein Becher seyn. W. Z. E.
45. Wenn man in allen drey Fällen den Schatten mit der Grundfläche parallel zerschneidet; so kommet überall ein Cricul heraus, und zwar sind im ersten Falle alle Circul einander gleich; im andern aber werden sie immer kleiner, und im dritten immer grösser, je weiter man von dem Körper hinaus kommet (§. 181. 186. Geom.).
46. Fanget den hellen Strahl des Lichtes, der durch ein kleines Löchlein in ein verfinstertes Gemach hineinfället, mit einem dreyeckigten prismatischen Glase auf; so werdet ihr, wenn ihr das Glas recht haltet, die schönsten Regenbogen-Farben sehen. Ihr möget die Strahlen auffangen hinter dem Glase, wo ihr wollet; so werden sie beständig die schönsten Farben vorstellen: ja so gar die Luftstäublein sehen schön gefärbet aus. Fanget sie mit einem Spiegel auf; so werdet [316] ihr die Farben wie sonst das Licht reflectiren. Lasset sie durch ein Brennglas fallen; so werden hinter dem Glase, wo sie noch weit von einander sind, auch nach der Refraction Farben bleiben. Hingegen unweit dem Brennpuncte und in demselben werdet ihr keine Farben, sondern Licht sehen, wenn ihr ein Papier dahin haltet. Hinter dem Brennpuncte fahren die Strahlen wieder weit aus einander, und machen abermal Farben.
47. Also kan das Licht in Farben, und die Farben können wieder in Licht verwandelt werden: und zwar geschiehet jenes, wenn die Strahen von einander gesondert; dieses aber, wenn sie mit einander vermenget werden. Denn es entstehen nicht allezeit Farben, wenn die Strahen des Lichtes durch einen grossen Raum ausgebreitet werden, die vorhin durch einen kleinen zerstreuet waren.
48. Eben dergleichen Strahlen entstehen, wenn ihr den Strahl des Sonnen-Lichtes LM in ein mit Wasser gefülletes Conisches Glas einfallen lasset. Und wenn dieses in einem verfinsterten Gemache geschiehet, formiren sie einen grossen, zuweilen doppelten Regenbogen. Man muß aber das Glas mit Wasser, eben als wie das geschliffene prismatische Glas so lange erhöhen und erniedrigen, bis die Strahlen unter dem rechten Winkel einfallen.
49. Die Körper haben also verschiedene Farben, weil sie die Strahlen des Lichtes auf verschiedene Art zurückwerfen.
[317]50. Ein Körper siehet von weiten dunkeler aus als in der Nähe.
Von jedem Puncte eines jeden erleuchteten Körpers fliessen unzählig viel Strahlen aus (§. 18.): sie fahren aber immer weiter von einander, je weiter man von dem Körper wegkommet (§. 9.). Derowegen können in der Nähe mehr Strahlen in die Augen fallen, als in der Weite, und also siehet er in der Nähe heller, in der Weite dunkeler aus W. Z. E.
51. Weil die weiten Sachen kleiner (§. 23.), in grossen Theilen undeutlicher (§. 26.) und dabey dunkeler (§. 50.) aussehen, als die nahen; so kan man auf einer Fläche verschiedene Dinge mahlen, deren eines weiter weg zu seyn scheinet, als das andere. Und auf diesem Grunde nebst dem Schatten, den die Körper werfen, beruhet die ganze Mahler-Kunst, als welche die cörperlichen Dinge auf einer Fläche dergestalt vorstellet, wie sie dem Auge in der Natur erscheinen.
52. Was unter Einem Winkel gesehen wird, siehet gleich groß aus: was unter einem grösseren gesehen wird, siehet grösser aus, und was unter einem kleineren gesehen wird, kleiner.
Weil zwey oder mehrere Sachen AC und ED unter Einem Winkel ABC gesehen werden; so ist das Bild im Auge von einerley Grösse. Und [318] eben so klar ist, daß das Bild der Sache grösser ist, welche unter einem grösseren Winkel gesehen wird, hingegen derjenigen kleiner, die man unter einem kleinern siehet. Derowegen müssen in dem ersten Falle die Sachen gleich groß aussehen: in dem andern aber siehet die erste grösser, und die andere kleiner aus (§. 23.). W. Z. E.

53. Wenn zwey Körper von verschiedener Grösse DE und AC gleich groß aussehen; so verhalten sie sich gegen einander wie ihre Weiten von dem Auge DB und AB.[Fig. 5]
Wenn zwey Körper gleich groß aussehen; so sind ihre Bilder im Auge von gleicher Grösse (§. 23.), und also machen die beiden äussersten Strahlen AB und CB in dem Auge B einerley Winkel. Da nun bey D und A rechte Winkel sind; so ist DE mit AC parallel (§. 73. Geom.), und daher DE:AC = DB:AB (§. 149. Geom.). W. Z. E.
54. Wenn die Bilder zweyer Sachen im Auge zusammenstossen; so scheinen sie uns nahe bey einander zu stehen.
Wenn zwey Sachen neben einander stehen; so sind auch ihre Bilder im Auge neben einander: welches ihr auch leicht auf dergleichen Weise erfahren könnet, wie oben angewiesen worden (§. 20. 30.). Alsdenn aber sehen wir auch die [319] Sachen neben einander. Wenn nun das Auge auf eben solche Art afficiret wird, als von neben einander stehenden Sachen geschiehet; so müssen sie uns auch neben einander zu stehen scheinen. Derowegen wenn die Bilder zweyer Sachen im Auge zusammen stossen; so scheinen uns dieselben nahe bey einander zu stehen. W. Z. E.
55. Die Bilder zweyer Sachen stehen in dem Auge neben einander, wenn von denen andern, die zwischen ihnen liegen, keine Strahlen ins Auge fallen können. Dannenhero kommet es uns vor, als wenn alle Sterne gleich weit von der Erde weg wären: als wenn einer, den wir von weiten sehen, an einem Walde gienge, da er doch einen ziemlichen Weg davon weg ist: als wenn zwey Thürme an einer Kirche wären, da sie doch in verschiedenen Dörfern sind, u. s. w.
56. Eine brennende Fackel, oder ein ander brennendes Licht, siehet in der Weite grösser aus, als in der Nähe.
Wenn ihr einen Sonnenstrahl durch ein kleines Loch in einen verfinsterten Ort fallen lasset; könnet ihr wahrnehmen, daß die Luft Stäublein von dem Lichte einen Glanz bekommen. Derowegen ist nicht zu zweifeln, und man kan es auch mit Augen sehen, daß die Luft um das Licht einen starken Glanz bekommet. In der Nähe könnet ihr ihn von der Flamme unterscheiden. Weil aber die Flamme schwächer aussiehet, wenn ihr von dem Lichte weit wegkommet (§. 9.); so haltet ihr den Glanz der Luft mit für einen Theil der Flamme: [320] dannenhero siehet euch die Flamme des Lichtes von weiten grösser aus, als in der Nähe. W. Z. E.
57. Da nun die glänzende Luft um und um die Flamme des Lichts umgiebet; so siehet sie uns auch von Weiten rund aus, unerachtet sie in der Nähe wie eine Pyramide zugespitzet ist.
58. Wenn die scheinbare Grösse des Raumes, dadurch sich ein Körper in einer merklichen Zeit beweget, unmerklich ist; so kan seine Bewegung nicht gesehen werden, sondern er scheinet stille zu stehen.
Wenn wir die Bewegung eines Cörpers sehen sollen; so muß sein Bild im Auge nicht auf Einer Stelle bleiben (§. 24.). Wenn aber die scheinbare Grösse des Raumes, dadurch sich der Körper in einer merklichen Zeit beweget, unmerklich ist, das ist, kaum einige Minuten, oder auch wol gar Sekunden hält; so muß das Bild im Auge auf einer Stelle bleiben (§. 25.). Derowegen können wir in diesem Falle keine Bewegung verspüren. W. Z. E.
59. Darum scheinen uns die Sachen, welche sich in der Nähe sehr langsam, als der Zeiger an einer Uhr, oder auch in einer grossen Weite sehr geschwinde, als die Sterne am Himmel, bewegen, stille zu stehen.
[321]60. Wenn die Bewegung der Körper von weiten gleich gemerket werden kan; so muß sie doch viel langsamer scheinen, als sie ist (§. 25.).
61. Dannenhero wenn zwey Körper sich gleich geschwinde bewegen, der eine aber weiter weg ist, als der andere; so wird der weitere sich langsamer zu bewegen scheinen.
62. Und also gewinnet es das Ansehen, als wenn der weitere zurücke bliebe; hingegen der nähere scheinet sich geschwinder zu bewegen, als würklich geschiehet.

63. Es sey das Auge in O, der erste Körper anfangs in V, der andere in T; so sehet ihr beide in S (§. 55.). Der Körper V beweget sich aus V in u, und der andere T aus T in t; so scheinet sich V aus S in N, und T nur aus S in M beweget zu haben.[Fig. 6]
64. Wenn das Auge O mit einem Körper V sich nach einer Gegend beweget, aber geschwinder als er; so kan er ihm zurücke zu gehen scheinen.[Fig. 6]
Es sey das Auge anfangs in O, und der Körper in V; so sehet ihr ihn in S. Das Auge beweget sich aus O in P, und der Körper aus V in u, also das Auge geschwinder als er. Wenn ihr nun zurücke sehet; so scheinet euch der Körper [322] in Q, und gewinnet demnach das Ansehen, als wenn er aus S in Q zurücke gegangen wäre. W. Z. E.
65. Wenn das Auge in Ansehung unseres Leibes und der Leib in Ansehung eines andern Körpers unbeweglich ist, beide aber mit diesem schnell fortbeweget werden: so scheinen sich die zu beiden Seiten unbewegliche Körper uns entgegen zu bewegen.
Wenn ihr auf einem Schiffe fahret, so scheinen sich die Ufer und Bäume an den Ufern euch entgegen zu bewegen. Eben so scheinen auch die Bäume euch entgegen zu kommen und vorbey zu gehen, wenn ihr schnell auf einem Postwagen fahret. Man soll die Ursache sagen, woher dieses komme.
Indem ihr auf dem Schiffe oder Wagen schnell fahret; so wird die Lage des Auges gegen die zu den Seiten liegende Körper geändert. Dannenhero kan das Bild davon nicht immer auf einer Stelle im Auge bleiben, und weil die Bewegung des Leibes geschwinde geschiehet, muß auch das Bild von einer Stelle geschwinde auf die andere fortrücken, ja die alten Bilder müssen immer verschwinden, und neue in deren Stelle kommen. Derowegen scheinen sich die im Auge abgebildeten Sachen, das ist, die zu beiden Seiten unbeweglich stehende Körper, uns entgegen zu bewegen und vorbey zu gehen (§. 24.). W. Z. E.
[323]66. Es kan auch zuweilen scheinen, als wenn ein unbeweglicher Körper euch entgegen käme. Z. E. ihr gehet auf dem Felde gegen einen Wald zu, und weit davon zu euch her stehet ein Baum. Weil ihr zwischen dem Baume und dem Walde nichts sehet, kommet es euch vor, als wenn er mit zu dem Walde gehörete (§. 55.). Wenn ihr aber näher hinkommet; fallen Strahlen von darzwischen gelegenen Sachen ins Auge, und bilden sie in ihm ab, und zwar immer mehrere, je näher er kommet. Derowegen wird das Bild des Baumes in dem Auge immer weiter von dem Walde weggerücket, und also scheinet er euch entgegen zu kommen (§. 24.).

