Die elektrischen Kräfte/Zusammenstellung:§46

« Zusammenstellung:§45	Carl Gottfried Neumann Die elektrischen Kräfte	Zusammenstellung:§47 »
fertig Fertig! Dieser Text wurde zweimal anhand der Quelle Korrektur gelesen. Die Schreibweise folgt dem Originaltext.
Für eine seitenweise Ansicht und den Vergleich mit den zugrundegelegten Scans, klicke bitte auf die entsprechende Seitenzahl (in eckigen Klammern).

§. 46. Fortsetzung. — Construction der Richtung der Determinante für einen unendlich kleinen Strom.

Es sei $\lambda _{1}$ die Fläche des unendlich kleinen Stromes, $n_{1}$ die positive Normale derselben; ferner seien $\alpha _{1},\beta _{1},\gamma _{1}$ die Richtungscosinus dieser Normale; ferner mögen die relativen Coordinaten des betrachteten Punctes $(x,y,z)$ in Bezug auf den Strom $\lambda _{1}\left(x_{1},y_{1},z_{1}\right)$ bezeichnet sein mit $\xi ,\eta ,\zeta ;$ so dass also

(25.)

$\xi =x-x_{1},\ \eta =y-y_{1},\ \zeta =z-z_{1};$

endlich sei $\Delta (\mathrm {A} ,\mathrm {B} ,\Gamma )$ die Determinante von $\lambda _{1}$ in Bezug auf jenen Punct.

In diesem Fall reducirt sich die Formel (16.) auf:

(26.)

${\mathsf {A}}=\Sigma _{\lambda _{1}},$

wo $\Sigma _{\lambda _{1}}$, nach (19.), den Werth hat:

$\Sigma _{\lambda _{1}}=\lambda _{1}{\frac {\partial }{\partial x_{1}}}\left(\alpha _{1}{\frac {\partial {\frac {1}{r}}}{\partial x_{1}}}+\beta _{1}{\frac {\partial {\frac {1}{r}}}{\partial y_{1}}}+\gamma _{1}{\frac {\partial {\frac {1}{r}}}{\partial z_{1}}}\right),$

also mit Rücksicht auf (25.) auch so dargestellt werden kann:

${\begin{array}{ll}\Sigma _{\lambda _{1}}&=\lambda _{1}{\frac {\partial }{\partial \xi }}\left(\alpha _{1}{\frac {\partial {\frac {1}{r}}}{\partial \xi }}+\beta _{1}{\frac {\partial {\frac {1}{r}}}{\partial \eta }}+\gamma _{1}{\frac {\partial {\frac {1}{r}}}{\partial \zeta }}\right),\\\\&=-\lambda _{1}{\frac {\partial }{\partial \xi }}\left({\frac {\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta }{r^{3}}}\right),\\\\&=-\lambda _{1}\left({\frac {\alpha _{1}}{r^{3}}}-{\frac {3\left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)}{r^{4}}}{\frac {\xi }{r}}\right).\end{array}}$

Somit folgt aus (26.) sofort:

(27.)

${\begin{array}{l}\mathrm {A} =-\lambda _{1}{\frac {\alpha _{1}r^{2}-3\xi \left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)}{r^{5}}};\ \mathrm {und\ ebenso\ wird} :\\\\\mathrm {B} =-\lambda _{1}{\frac {\beta _{1}r^{2}-3\eta \left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)}{r^{5}}},\\\\\Gamma =-\lambda _{1}{\frac {\gamma _{1}r^{2}-3\zeta \left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)}{r^{5}}}.\end{array}}$

Diese Formeln führen in Betreff der Determinante $\Delta$ oder $\mathrm {A} ,\mathrm {B} ,\Gamma$ zu folgender Construction:

Man theile die von dem unendlich kleinen Strom $\lambda _{1}$ nach dem gegebenen Punct $P$ gehende Linie $r$ in drei gleiche Theile, und lege durch den $\lambda _{1}$ zunächst liegenden Theilpunct $Q$ eine gegen $r$ perpendiculäre Ebene. Bezeichnet $R$ denjenigen Punct, in welchem diese Ebene von der positiven Normale $n_{1}$ des Stromes getroffen wird, so wird jene Determinante $\Delta$ die Richtung $PR$ (oder vielleicht auch die entgegengesetzte Richtung $RP$) besitzen^[1].

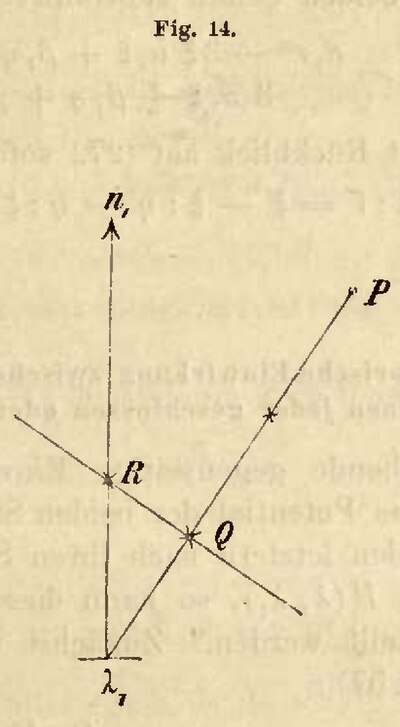
Fig. 14.

Beweis.— Die Coordinaten des gegebenen Punctes $P$ sind [vergl. (25.)]:

$\xi ,\eta ,\zeta ,\,$

folglich die Coordinaten des genannten Theilpunctes $Q$:

${\frac {1}{3}}\xi ,\ {\frac {1}{3}}\eta ,\ {\frac {1}{3}}\zeta .$

Zur Bestimmung der Coordinaten $\xi ',\eta ',\zeta '$ des Punctes $R$ ergeben sich daher die Gleichungen:

(a.)	$\left(\xi '-{\frac {1}{3}}\xi \right)\xi +\left(\eta '-{\frac {1}{3}}\eta \right)\eta +\left(\zeta '-{\frac {1}{3}}\zeta \right)\zeta =0,$

(b.)	$\xi '=\vartheta \alpha _{1},\ \eta '=\vartheta \beta _{1},\ \zeta '=\vartheta \gamma _{1},$

wo $\vartheta$ einen unbekannten Factor vorstellt.

Die Gleichung (a.) kann auch so geschrieben werden:

(c.)	$\xi '\xi +\eta '\eta +\zeta '\zeta ={\frac {1}{3}}r^{2},$

oder mit Rücksicht auf (b.) auch so:

(d.)	$\vartheta \left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)={\frac {1}{3}}r^{2}.$

Substituirt man den hieraus für $\vartheta$ sich ergebenden Werth in die erste der Formeln (b.), so folgt:

(e.)	$\xi '={\frac {\alpha _{1}r^{2}}{3\left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)}},$

oder falls man $\xi$ auf beiden Seiten subtrahirt:

(f.)	$\xi '-\xi ={\frac {\alpha _{1}r^{2}-3\xi \left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)}{3\left(\alpha _{1}\xi +\beta _{1}\eta +\gamma _{1}\zeta \right)}}.$

Hieraus aber folgt mit Rückblick auf (27.) sofort:

(g.)	$\mathrm {A} :\mathrm {B} :\Gamma =\xi '-\xi :\eta '-\eta :\zeta '-\zeta ;\,$

w. z. z. w.

---

1. Die Linie $PR$ ist in der Figur nicht gezeichnet.