Mathematische Principien der Naturlehre/Buch2-I
| ← Buch I. Abschnitt XIV. | Mathematische Principien der Naturlehre (1872) von Isaac Newton, übersetzt von Jakob Philipp Wolfers Buch II. Abschnitt I. |
Buch II. Abschnitt II. → |
§. 1. Lehrsatz. Ein Körper, welcher einen seiner Geschwindigkeit proportionalen Widerstand erleidet, verliert einen dem zurückgelegten Wege proportionalen Theil seiner Bewegung.
Da nämlich die, in den einzelnen gleichen Zeittheilchen verlorene Bewegung sich wie die Geschwindigkeit verhält, d. h. wie die Theilchen des zurückgelegten Weges; so erhält man durch Zusammensetzung den in der ganzen Zeit erlittenen Verlust an Bewegung dem ganzen Wege proportional. W. z. b. w.
Zusatz. Wenn daher ein von aller Schwere freier Körper, vermöge eines ihm beigebrachten Anstosses, sich im freien Raume bewegt, und sowohl die ganze anfängliche, als auch die nach Zurücklegung eines bestimmten Weges übrige Bewegung gegeben ist; so kennt man auch den ganzen Weg, welchen der Körper in unbestimmter Zeit zurücklegen kann. Es verhält sich nämlich der letztere Weg zu dem schon zurückgelegten Wege, wie die ganze anfängliche Bewegung zu dem bereits verlorenen Theile derselben.
§. 2. Lehrsatz. Grössen, welchen ihren Unterschieden proportional sind, sind selbst stetig proportional.
Aus
folgt nämlich
W. z. b. w.
§. 3. Lehnsatz. Erleidet ein Körper einen seiner Geschwindigkeit proportionalen Widerstand, und bewegt er sich nur vermöge eines, durch eine Kraft ihm beigebrachten Anstosses, in einem gleichartigen Mittel und werden endlich die Zeittheile als gleich angenommen; so stehen die Geschwindigkeiten im Anfange der einzelnen Zeittheile in geometrischer Progression, und es verhalten sich die in den einzelnen Zeiten beschriebenen Wege wie die Geschwindigkeiten.
Erster Fall. Ist die Zeit in gleiche Stücke getheilt, und wirkt im Anfange eines jeden der letzteren, die der Geschwindigkeit proportionale Kraft des Widerstandes durch einen einzelnen Stoss; so verhält sich die Abnahme der Geschwindigkeit in den einzelnen Zeittheilchen wie dieselbe Geschwindigkeit. Die Geschwindigkeiten sind daher ihren Unterschieden proportional und stehen mithin (nach §. 2.) selbst in stetiger Proportion.[1] Setzt man nun aus einer gleichen Anzahl von Zeittheilchen beliebige gleiche Zeiten zusammen, so verhalten sich die Geschwindigkeiten im Anfange dieser Zeiten selbst, wie diejenigen Glieder einer stetigen Progression, welche man sprungweise genommen hat, indem man immer eine gleiche Anzahl zwischenliegender Glieder überschlägt. Die Verhältnisse dieser Glieder werden aber aus den, gleich oft wiederholten, gleichen Verhältnissen der zwischenliegenden Glieder zusammengesetzt, und sind daher gleich.[2] Die diesen Gliedern proportionalen Geschwindigkeiten stehen demnach in geometrischer Progression. Vermindert man in’s Unendliche jene gleichen Zeittheilchen und vermehrt man ebenso ihre Anzahl so weit, das der Impuls des Widerstandes ein stetiger wird; so werden die im Anfange der gleichen Zeiten immer stetig proportionalen Geschwindigkeiten auch in diesem Falle in stetiger Proportion stehen. W. z. b. w.
Zweiter Fall. Aus dem Obigen folgt auch, dass die Unterschiede der Geschwindigkeiten, d. h. die in den einzelnen Zeiten verlorenen Theile derselben sich wie die ganzen Geschwindigkeiten verhalten. Die in den einzelnen Zeiten beschriebenen Wege verhalten sich aber (nach §. 1.) wie die verlorenen Theile der Geschwindigkeiten und daher wie diese selbst. W. z. b. w.

Zusatz. Man beschreibe zu den rechtwinkligen Asymptoten ADC und CH die Hyperbel BG und ziehe AB und GD auf AC perpendikulär. Drückt man nun sowohl die Geschwindigkeit des Körpers, als auch den Widerstand des Mittels im Anfange der Bewegung durch die beliebige constante Linie AC, nach Verlauf einiger Zeit aber durch die unbestimmte Linie DC aus; so kann die Zeit durch die Fläche ABGD, und der in derselben beschriebene Weg durch die Linie AD ausgedrückt werden.[3] Wird nämlich jener Flächenraum nach der Weise der Zeit gleichförmig durch die Bewegung des Punktes D vergrössert; so wird DC in geometrischem Verhältniss nach der Weise der Geschwindigkeit vermindert und es nehmen die in gleichen Zeiten beschriebenen Theile der Geraden AC in demselben Verhältniss ab.
§. 4. Aufgabe. Ein Körper steigt in einem ähnlichen Mittel geradlinig auf oder ab, und dieses widersteht im Verhältniss der Geschwindigkeit, ferner wirkt auf jenen die gleichförmige Kraft der Schwere; man soll eine Bewegung bestimmen.
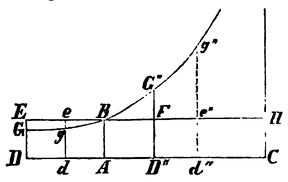
Steigt der Körper auf, so werde die Schwere durch das beliebige gegebene Rechteck BACH, und der Widerstand des Mittels, im Anfang des Aufsteigens, durch das auf der entgegengesetzten Seite liegende Rechteck ABED ausgedrückt. Zu den rechtwinkligen Asymptoten AC und CH beschreibe man eine, durch den Punkt B gehende, Hyperbel, welche die Perpendikel DE und de in G und g schneidet. Alsdann wird der Körper
| aufsteigend | in der Zeit | DGgd | den Raum | EGge |
| „ „ „ | DGBA | „ „ | EGB | |
| absteigend | „ „ „ | ABG"D" | den Raum | BFG" |
| „ „ „ | B"G"g"d" | „ „ | FG"g"e" |
beschreiben, und die Geschwindigkeiten des Körpers (welche den Widerständen des Mittels proportional sind) werden in den Perioden dieser Zeiten respective sein:

Die grösste Geschwindigkeit, welche der Körper absteigend erlangen kann, wird sein:
Man löse das Rechteck ABHC in unzählige kleinere
auf, welche sich wie die, in eben so vielen gleichen Zeiten erfolgten Incremente der Geschwindigkeiten verhalten. Alsdann sind
den ganzen Geschwindigkeiten proportional, d. h. (nach der Voraussetzung) dem Widerstande des Mittels im Anfange der einzelnen gleichen Zeiten. Nun verhalte sich
wie die Kraft der Schwere zum Widerstande im Anfange des zweiten Zeitraumes. Zieht man von der Kraft der Schwere den jedesmaligen Widerstand ab, so bleiben
übrig, welche sich wie die absoluten Kräfte verhalten, durch die der Körper im Anfange der einzelnen Zeiträume angetrieben wird; folglich (nach Gesetz II. der Bewegung) wie die Incremente der Geschwindigkeiten, d. h. wie die Rechtecke
Sie stehen daher nach §. 2.) in geometrischer Progression. Schneiden die verlängerten geraden Linien
die Hyperbel in den Punkten
so sind die Flächen
einander gleich, und daher sowohl den Zeiten, als auch den immer gleichen Kräften der Schwere analog.
Es ist aber (nach erstem Buche, §. 7., Zusatz 3. und §. 8.)
d. h. wie die Kraft der Schwere zum Widerstande in der Mitte des ersten Zeitraumes.
Aus demselben Grunde verhalten sich die Flächen
zu den Flächen
wie die Kraft der Schwere zum Widerstande in der Mitte des zweiten, dritten, vierten u. s. w. Zeitraumes.
Da ferner die gleichen Flächen
der jedesmaligen Kraft der Schwere analog sind; so sind die Flächen
dem Widerstande in der Mitte der einzelnen Zeiträume, d. h. (nach der Voraussetzung) den Geschwindigkeiten, folglich den beschriebenen Wegen analog. Nimmt man nun die Summen analoger Grössen, so sind die Flächen
den ganzen beschriebenen Wegen, und auch die Flächen
den Zeiten analog.
Der Körper beschreibt daher beim Absteigen in jeder Zeit
den Raum
und in der Zeit LrtN den Weg lrtn. W. z. b. w.
Auf gleiche Weise wird die dargestellte Bewegung während des Aufsteigens erwiesen.
Zusatz 1. Die grösste Geschwindigkeit, welche der Körper während des Niedersteigens erlangen kann, verhält sich daher zu der in jeder gegebenen Zeit erlangten Geschwindigkeit, wie die constante Kraft der Schwere, welche beständig auf ihn einwirkt, zu derjenigen Kraft, welche der Widerstand am Ende jener Zeit ihm entgegenstellt.[5]
Zusatz 2. Nimmt die Zeit in arithmetischer Progression zu, so nimmt die Summe jener grössten Geschwindigkeit und der Geschwindigkeit beim Aufsteigen (wie auch ihre Differenz beim Absteigen) in geometrischer Progression ab.[6]
Zusatz 3. Auch die Unterschiede der Wege, welche in gleichen Zeitintervallen beschrieben werden, nehmen in derselben geometrischen Progression ab.[7]
Zusatz 4. Der durch einen Körper beschriebene Raum ist aber dem Unterschiede zweier Räume gleich, deren einer sich wie die Zeit vom Anfang des Absteigens an, deren anderer sich wie die Geschwindigkeit verhält und welche beide Räume im Anfange des Absteigens einander gleich sind.[8]

§. 5. Aufgabe. Es wird vorausgesetzt, dass in irgend einem ähnlichen Mittel die Schwere gleichförmig wirke und perpendikulär gegen die Ebene des Horizonts gerichtet sei; man soll die Bewegung eines Projectils bestimmen, welches im Mittel einen der Geschwindigkeit proportionalen Widerstand erleidet.
Vom Punkte D aus gehe das Projectil längs der beliebigen geraden Linie DP fort, und es drücke die Länge der letztern seine Geschwindigkeit im Anfange der Bewegung aus. Vom Punkte P fälle man auf die horizontale Linie DC das Perpendikel PC und schneide DC so in A, dass DA sich zu AC verhalte, wie der, aus der anfänglichen nach oben gerichteten Bewegung entstandene, Widerstand zur Schwere oder (was dasselbe ist), dass
verhalte, wie der ganze Widerstand im Anfange der Bewegung zur Kraft der Schwere.[9] Nun beschreibe man eine beliebige Hyperbel GTBS, welche die errichteten Perpendikel DG und AB in G und B schneidet und vollende das Parallelogramm DGKC, dessen Seite GK die Linie AB in Q schneidet. Bestimmt man nun eine Linie N so, dass
und errichtet man in dem beliebigen Punkte R der Linie DC das Perpendikel RT, welches die Hyperbel in T und die Linien EH, GK, DP in J, t, V schneidet; nimmt man ferner auf demselben
also
und ferner
Die Zeit werde nun durch die Fläche RDGT ausgedrückt, und (nach Gesetze, Zusatz 2.) die Bewegung des Körpers in zwei zerlegt, die eine perpendikulär nach oben, die andere horizontal seitwärts gerichtet. Da ferner der Widerstand der Bewegung proportional ist, so wird man auch diesen in zwei zerlegen können, welche den beiden Seitenbewegungen proportional und entgegengesetzt sind. Die Länge der horizontal gerichteten Seitenbewegung ist (nach dem zweiten Buche, §. 3.) der Linie DR, die aufwärts gerichtete Bewegung aber (nach dem zweitem Buche, §. 4.)
Beim Anfange der Bewegung selbst ist aber
daher in diesem Falle (nach 4.)
oder
d. h. es verhält sich Rr zu Dr, wie die anfängliche aufwärts gerichtete Bewegung zu der horizontalen.
Da nun Rr immer der aufwärts gerichteten, und DR der horizontalen Bewegung proportional ist, da ferner im Anfange Rr sich zu DR wie die erstere zur letzteren verhält; so muss
nothwendig immer das Verhältniss beider Seitenbewegungen ausdrücken, und der Körper sich daher in der Curve DraF bewegen, in welcher der Punkt r beständig liegt. W. z. b. w.
Zusatz 1. Es ist daher Rr = (Gl. 4). Verlängert man nun RT bis X, so dass
werde, d. h. wenn man das Parallelogramm ACPY vollendet, die Linie DY die CP in Z schneidet und RT verlängert, bis sie DY in X schneidet; so wird
also der Zeit proportional.
Zusatz 2. Nimmt man also unzählige Linien CR, oder was dasselbe ist, ZX in geometrischer Progression, so ergeben sich eben so viel Linien Xr in arithmetischer Progression. Hiernach kann man die Curve DraF leicht mittelst der Logarithmentafeln construiren.
Zusatz 3. Man construire zum Scheitel D mit einem abwärts verlängerten Durchmesser DG und einem Parameter, welcher sich zu 2 · DP verhält, wie der ganze Widerstand im Anfange der Bewegung zur Kraft der Schwere, eine Parabel. Alsdann wird die Geschwindigkeit, mit welcher der Körper vom Orte D längs DP ausgehen muss, um im gleichförmig widerstehenden Mittel die Curve DraF zu beschreiben, dieselbe sein, mit welcher er von demselben Punkte längs DP ausgehen muss, um im nicht widerstehenden Mittel die Parabel zu beschreiben.
Der Parameter dieser Parabel ist nämlich im Anfange der Bewegung selbst
und
Die gerade Linie, welche, wenn sie gezogen wäre, die Hyperbel GTS in G berühren würde, ist parallel DK, mithin
oder
Ferner war (Gl. 1 )
daher wird
oder weil
und so der Parameter, oder
d. h. weil
und so
oder
Zusatz 4. Wird demnach ein Körper von einem gegebenen Orte D, mit gegebener Geschwindigkeit längs einer, der Lage nach gegebenen, geraden Linie DP geworfen und ist der Widerstand des Mittels beim Anfange der Bewegung bekannt; so kann man die Curve DraF bestimmen, welche derselbe beschreiben wird.
Aus der gegebenen Geschwindigkeit erhält man nämlich den Parameter der Parabel, wie bekannt.[11] Aus der Proportion 11. erhält man hierauf DP. Schneidet man nun CD so in A, dasswird, so erhält man den Punkt A und daraus die Curve DraF.
Zusatz 5. Ist umgekehrt die Curve DraF gegeben, so kennt man auch die Geschwindigkeit des Körpers und den Widerstand des Mittels in den einzelnen Orten r. Aus dem gegebenen Verhältniss
erhält man sowohl den Widerstand des Mittels beim Anfang der Bewegung, als auch den Parameter der Parabel und hieraus dann auch die anfängliche Geschwindigkeit der Bewegung. Aus der Länge der Tangente rL ergiebt sich die ihr proportionale Geschwindigkeit und der der letzteren proportionale Widerstand im beliebigen Punkte r.
Zusatz 6. Es verhält sich 2 · DP zum Parameter der Parabel, wie die Schwere zum Widerstande im Punkte D. Nimmt die Geschwindigkeit zu, so wächst der Widerstand ihr proportional, wogegen der Parameter im doppelten Verhältniss zunimmt. Offenbar wird also die Länge 2 · DP in jenem einfachen Verhältniss wachsen und ist daher immer der Geschwindigkeit proportional [12], auch wird sie durch Veränderung des Winkels CDP weder grösser noch kleiner, wenn nicht die Geschwindigkeit sich verändert.


Zusatz 7. Hieraus ergiebt sich eine Methode, um sehr nahe aus den Erscheinungen die Curve DraF zu bestimmen, und daraus dann den Widerstand und die Geschwindigkeit, womit der Körper geworfen wird, herzuleiten. Es werden zwei gleiche und ähnliche Körper mit derselben Geschwindigkeit vom gegebenen Orte D aus geworfen, und zwar unter verschiedenen Winkeln CDP und cDp (wo die kleinen Buchstaben sich auf unterhalb gelegene Orte beziehen), und man kenne die Punkte F und f, wo die Körper in die horizontale Ebene DC fallen. Nimmt man hierauf für DP oder Dp eine beliebige Länge an, so denke man sich, dass der Widerstand in D zur Schwere in irgend einem Verhältniss stehe und drücke dieses Verhältniss durch die beliebige Länge SM aus. Hierauf findet man durch Rechnung aus der angenommenen Länge DP die Längen DF und Df und subtrahire nun von dem, durch Rechnung gefundenen, Verhältniss
das durch Versuch gefundene, und drücke den Unterschied durch das Perpendikel MN aus. Dies wiederhole man zum zweiten und dritten Mal, indem man immer ein neues Verhältniss SM des Widerstandes zur Schwere annimmt und den neuen Unterschied durch ein neues MN ausdrückt. Man errichte die positiven Unterschiede nach der einen, die negativen nach der entgegengesetzten Seite von SM, ziehe hierauf durch die Punkte N die regelmässige Curve NNN, welche die Linie SMMM in X schneidet; es wird alsdann SX das wahre Verhältniss des Widerstandes zur Schwere sein, welches man sucht. Aus diesem Verhältniss hat man die Länge DF durch Rechnung herzuleiten, und es wird alsdann diejenige Linie, welche sich zur angenommenen Länge von DP verhält, wie die eben gefundene Länge von DF zu der durch Versuch erhaltenen, die wahre Länge von DP sein. Hat man diese gefunden, so kennt man die Curve DraF, welche der Körper beschreibt, seine Geschwindigkeit und den Widerstand in den einzelnen Punkten.
§. 6. Anmerkung. Uebrigens ist die Hypothese, dass der Widerstand der Geschwindigkeit proportional sei, mehr eine mathematische, als eine der Natur entsprechende. Dieses Verhältniss findet sehr nahe statt, wenn Körper in ziemlich festen Mitteln sich sehr langsam bewegen. In Mitteln aber, welche von aller Festigkeit frei sind, finden die Körper einen Widerstand, welcher (wie später bewiesen werden wird) im doppelten Verhältniss der Geschwindigkeit steht. Durch die Wirkung des geschwinderen Körpers wird derselben Menge des Mittels in kürzerer Zeit eine, im Verhältniss der grössern Geschwindigkeit, grössere Bewegung und in gleicher Zeit (wegen der grössern Menge des gestörten Mittels) eine im doppelten Verhältniss grössere Bewegung mitgetheilt und es ist (nach Gesetz II. und III. der Bewegung) der Widerstand der mitgetheilten Bewegung proportional. Wir wollen sehen, was für Bewegungen aus diesem Gesetze des Widerstandes hervorgehen.
Bemerkungen und Erläuterungen [des Übersetzers]
[Bearbeiten]- ↑ [595] No. 82. S. 231. Ist die ganze Zeit t = nτ gesetzt, wo n beliebig gross, so bilde man folgendes Tableau:
Zeittbeile: τ, 2τ, 3τ, 4τ, etc. . . nτ Geschwindigkeiten: v, vI, vII, vIII, etc. Decremente der Geschwindigkeit: av, avI, arII, avIII, etc. Alsdann ist
v — av = vI, vI — avI = vII, vII — avII = vIII, vIII — avIII = vIV = etc.,
also auch
v : v — vI = vI : vI — vII = vII : vII - vIII = vIII : vIII — vIV = etc. =
und nach §. 2. v : vI = vI : vII = vII : vIII = vIII : vIV = etc.
- ↑ [595] No. 83. S. 231. Aus dem vorhergehenden Tableau erhält man z. B.
eben so vIV : vVIII = ; mithin vIV = a4v, vVIII = a4 · vIV = a8 · v.
- ↑ [595] No. 84. S. 231. (Fig. 133.) Setzt man CD = x und DG = y, so ist die Gleichung der Hyperbel
1. xy = a, wo a constant, Die hyperbolische Fläche wird daher
2. = a log. hyp. x = log. hyp. (xa). Eine zweite hyperbolische Fläche sei
3. AI = log. hyp. (xIa) Setzt man nun voraus, dass AI — A = Constans sei, so wird offenbar log. (xIa) — log. (xa) = log. = Constans oder auch
4. xI : x = Constans. - ↑ [595] No. 85. S. 233. (Fig. 135.) Nach den Lehren der Kegelschnitte ist für eine Hyperbel CK · Kq = CA · AB = Constans, also CK : CA = AB : Kq, CA : CA — CK = Kq : Kq — AB, d. h. CA : AK = Kq : qk und hieraus CA : ½AH = Kq : ½qk.
- ↑ [595] No. 86. S. 233. Es ist nämlich
ABHC : KkHC = AC : KC = AC : AC — AK. - ↑ [595] No. 87. S. 234. Wenn
ANtB — AMsB = AMsB — ALrB = ALrB — AKqB = AKqB ist, so wird auch
ABHC — ABnN : ABHC — ABmM = ABHC — ABmM : ABHC — ABlL = ABHC — ABlL : ABHC — ABkK d. h.
CN : CM = CM : CL = CL : CK wie aus der Bemerkung 84. hervorgeht.
- ↑ [596] No. 88. S. 234. Aus ABqK : Bkq = ½AK, qKlr : gktr = AC : ½KL, rLMs : rlms = AC : ½LM, sMNt : smnt = AC : ½MN etc. etc. folgt für gleiche Intervalle, wo ABqK = qKLr = rLMs = sMNt = etc.
Bkq : gklr : rlms : smnt : etc. = AK : KL : LM : MN : etc. Das zweite fortlaufende Verhältniss ist mit dem in Bemerkung 84. identisch. - ↑ [596] No. 89. S. 234, Z. B. Bms = ABsm — ABmM.
- ↑ [596] No. 90. S. 234. Ist R der ganze Widerstand im Anfange der Bewegung, welcher der Geschwindigkeit DP proportional ist, so wird der, der nach oben gerichteten Bewegung entsprechende und CP proportionale, Widerstand R(a) und man hat, wenn G die Kraft der Schwere bezeichnet,
AD : AC = R(a) : G, DP : CP = R : R(a), also
AD · DP : AC · CP — R : G. - ↑ [596] No. 91. S. 236. Die Proportion QB : CK = DA : AC ergiebt sich, wie in §. 3. aus AC · AB = DC · DG oder AC : DC = DG : AB.
- ↑ [596]

Fig. 246. No. 92. S. 236. Drückt AB diese Geschwindigkeit, BC die ihr entsprechende Fallgeschwindigkeit aus, so ist der Parameter = .
- ↑ [596] No. 93. S. 237. Man setze den Parameter = p, die Kraft der Schwere constant = g, den Widerstand = r, die Geschwindigkeit = v; alsdann ist, wenn a, b, c constante Grössen bezeichnen, 2 · DP : p = g : r (Gl. 11.), p = av², r = bv, 2 · DP = = cv also der Geschwindigkeit proportional.
| ← Buch I. Abschnitt XIV. | Nach oben | Buch II. Abschnitt II. → |
| Dieser Text wurde anhand der angegebenen Quelle einmal Korrektur gelesen. Die Schreibweise sollte dem Originaltext folgen. Es ist noch ein weiterer Korrekturdurchgang nötig. |

























