Mathematische Principien der Naturlehre/Buch3-II
| ← Buch III. Abschnitt I. | Mathematische Principien der Naturlehre (1872) von Isaac Newton, übersetzt von Jakob Philipp Wolfers Buch III. Abschnitt II. |
Buch III. Abschnitt III. → |
§. 29. Aufgabe. Man soll die Kräfte der Sonne finden, womit sie die Bewegungen des Mondes stört.
Es bezeichne S die Sonne, T die Erde, P den Mond und CADB die Bahn des letzteren. Es sei SK = ST und SL : SK = SK² : SP². Ferner sei LM ∥ PT. Wird nun die beschleunigende Schwerkraft der Erde gegen die Sonne durch ST oder SK ausgedrückt, so wird SL die beschleunigende Schwerkraft des Mondes gegen die Sonne sein, und zwar ist diese aus den Theilen SM und ML zusammengesetzt, von denen LM und der Theil TM von SM die Bewegungen des Mondes stören, wie wir im ersten Buche, §. 107. nebst Zusätzen gesehen haben.
Die Erde und der Mond bewegen sich um ihren gemeinschaftlichen Schwerpunkt, daher wird die Bewegung der ersteren ebenfalls durch ähnliche Kräfte gestört. Man kann jedoch die Summe dieser Kräfte und Bewegungen auf den Mond beziehen und erstere durch analoge Linien TM und LM darstellen.
Die Kraft LM, in ihrem mittleren Werthe, steht zur Centripetalkraft, vermöge welcher der Mond sich in seiner Bahn, im Abstande PT um die als ruhend angenommene Erde bewegen könnte, im doppelten Verhältniss der Umlaufszeit des Mondes um die Erde, zur Umlaufszeit der letzteren um die Sonne (nach §. 107., Zusatz 17. des ersten Buches). Das Verhältniss ist demnach
Nun haben wir in §. 4. dieses Buches gefunden, dass, wenn die Erde und der Mond sich um ihren gemeinschaftlichen Schwerpunkt bewegen, ihre mittlere Entfernung sehr nahe 60½ Erdhalbmessern gleich ist. Ferner verhält sich die Kraft, vermöge welcher der Mond sich in seiner Bahn um die ruhende Erde und im Abstande PT = 60½ Erdhalbmessern bewegen könnte, zu derjenigen Kraft, vermöge welcher er sich in derselben Zeit, in einem Abstande von 60 Erdhalbmessern herumbewegen könnte, wie 60½ : 60.Endlich verhält sich diese Kraft zur Schwerkraft auf der Erde sehr nahe, wie 1 : 60². Es verhält sich daher die mittlere Kraft ML zur Schwerkraft an der Oberfläche der Erde, wie 1 · 60½ : 60³ · 17829/40 = 1 : 638092,6[2]. Hieraus und aus dem Verhältniss der Linien TM und ML ist die Kraft TM zu finden und dies sind die Kräfte der Sonne, wodurch die Bewegungen des Mondes gestört werden.
§. 30. Aufgabe. Man soll die stündliche Zunahme der, durch den Mond um die Erde beschriebenen Fläche bestimmen, vorausgesetzt, dass die Bahn kreisförmig sei.
Wir haben gesehen, dass die vom Radius des Mondes um die Erde beschriebenen Flächenräume den Zeiten proportional sind, so weit nicht durch die Einwirkung der Sonne die Bewegungen des Mondes gestört werden. Wir wollen nun untersuchen, welche Ungleichheit des Momentes oder der stündlichen Zunahme hierdurch hervorgebracht wird. Um die Rechnung zu erleichtern, wollen wir die Mondbahn als kreisförmig voraussetzen und alle Ungleichheiten vernachlässigen, mit Ausnahme derjenigen, von der hier die Rede ist.
Wegen der grossen Entfernung der Sonne nehmen wir an, dass SP und ST einander parallel seien. Hierdurch wird die mittlere Kraft LM auf ihren mittleren Werth TP, so wie die Kraft TM auf ihren mittleren Werth 3 · PK reducirt. Diese Kräfte bilden, nach Gesetze, Zusatz 2., durch Zusammensetzung die Kraft TL, welche indem man LE perpendikulär auf den Radius TP zieht, sich in die beiden Seitenkräfte TE und EL zerlegen lässt. Die erste von diesen, TE wirkt immer längs des Radius TP, und wird die Beschreibung der durch den letzteren durchlaufenen Fläche TPC weder beschleunigen noch verzögern. Was die zweite Seitenkraft EL anbelangt, so wirkt sie längs der auf den Radius perpendikulären Linie und beschleunigt oder verzögert jene Beschreibung eben so sehr, als sie die Bewegung des Mondes beschleunigt oder verzögert. Diese Beschleunigung des letzteren, welche in jedem Augenblicke beim Uebergange von der Quadratur C zur Conjunction A erfolgt, ist der beschleunigenden Kraft EL selbst, d. h. proportional. Die Zeit werde durch die mittlere Bewegung, oder (was fast auf dasselbe herauskommt) durch den Winkel CTP oder den Bogen CP dargestellt. Man ziehe CG perpendikulär auf CT und mache CG = CT; man denke sich ferner den Quadranten AC in unendlich viele gleiche Theile Pp, etc. getheilt, welche eben so viel gleiche Zeittheile darstellen. Man ziehe ferner pk perpendikulär auf CT und die Linie TG, welche die verlängerten Linien KP und kp in F und f schneidet. Offenbar ist nun FK = TK und Kk : PK = Pp : TP[3] d. h. Kk im gegebenen Verhältniss. Es wird daher FK · Kk oder die Fläche FKkf proportional , d. h. EL; folglich wird die ganze Fläche GCKF der Summe aller Kräfte EL, welche während der ganzen Zeit CP auf den Mond gewirkt haben, proportional. Jene Fläche ist also der Geschwindigkeit proportional, welche alle diese Kräfte hervorgebracht haben, d. h. der Beschleunigung, womit die Fläche CTP beschrieben wird, oder dem Increment des Moments.
Die Kraft, vermöge welcher der Mond seinen Umlauf um die als ruhend angenommene Erde, im Abstande TP und in der Zeit ADBC = 27d 7h 43m zurücklegen könnte, würde bewirken, dass ein fallender Körper während der Zeit CT den Weg ½CT durchliefe und in derselben Zeit eine Geschwindigkeit erlangte, welche derjenigen des Mondes in seiner Bahn gleich wäre. Dies erhellt aus §. 18., Zusatz 9. des ersten Buches. Da nun das auf TP gefällte Perpendikel Kd = ⅓EL und auch in den Octanten = ½TP oder = ½ML ist; so wird die Kraft EL in den Octanten, wo sie am grössten ist, die Kraft ML im Verhältniss 3 : 2 übertreffen. Sie wird sich daher zu der Kraft, vermöge welcher der Mond sich um die ruhende Erde in seiner Umlaufszeit bewegen könnte, verhalten wie 100 : ⅔ · 17872,5 (§. 29.) = 100 : 11915. In der Zeit CT müsste sie eine Geschwindigkeit hervorbringen, welche 100/11915 der Geschwindigkeit des Mondes gleich wäre, und während der Zeit CPA müsste sie eine Geschwindigkeit erzeugen, welche im Verhältniss CA : CT oder CA : TP grösser wäre.
Die grösste Kraft EL in den Octanten werde durch die Fläche FK · Kk = ½TP · Pp[4] dargestellt. Die Geschwindigkeit, welche die grösste Kraft in einer beliebigen Zeit CP hervorbringen könnte, wird sich alsdann zu der Kraft, welche durch die kleinste ganze Kraft EL erzeugt werden kann, verhalten wie ½TP · CP : KCGF, und die während der ganzen Zeit CPA erzeugten Geschwindigkeiten wie ½TP · CA : TCG = CA : TP.
Die Geschwindigkeit am Ende der ganzen Zeit wird also 100/11915 der Geschwindigkeit des Mondes gleich sein. Addirt und subtrahirt man von der letzteren, welche dem mittleren Momente der Fläche analog ist, die Hälfte von jener Geschwindigkeit und stellt man das mittlere Moment durch die Zahl 11915 dar; so wird die Summe 11915 + 50 = 11965 das grösste Moment der Fläche in den Syzygien, und der Unterschied 11915 – 50 = 11865 das kleinste Moment derselben Fläche in den Quadraturen darstellen.[5] Die während gleicher Zeiten in den Syzygien und Quadraturen beschriebenen Flächen verhalten sich daher zu einander, wie 11965 : 11865. Addirt man zum kleinsten Moment 11865 ein anderes, welches sich zum Unterschiede 100 beider verhält, wie FKCG : TCG oder (was dasselbe ist) wie PK² : PT² = Pd : PT;[6] so wird die Summe das Moment der Fläche in dem Falle darstellen, wo der Mond sich in einem beliebigen zwischenliegenden Orte P befindet.
Alles dieses findet unter der Voraussetzung statt, dass die Sonne und die Erde sich in Ruhe befinden, und der Mond seinen Umlauf in der synodischen Zeit von 27d 7h 43m vollende. Die wahre synodische Umlaufszeit beträgt aber 29d 12h 44m und daher müssen die Incremente der Momente im Verhältniss der Umlaufszeiten, d. h. im Verhältniss 1080853 : 1000000 vergrössert werden. Auf diese Weise wird das ganze Increment, welches 100/11915 vom mittleren Momente betrug, jetzt 100/11023 desselben werden. Es wird daher das Moment der Fläche in den Quadraturen des Mondes sich zum entsprechenden Moment in den Syzygien verhalten, wie 11023 – 50 : 11023 + 50 = 10973 : 11073; und zum Moment, wenn der Mond sich in einem beliebigen zwischenliegenden Orte P befindet, wie 10973 : 10973 + Pd, vorausgesetzt das TP = 100 sei.
Die Fläche, welche der Mond um die Erde in jedem gleichen Zeittheilchen beschreibt, ist also sehr nahe der Summe aus der Zahl 219,46 und dem Sinus versus des doppelten Abstandes des Mondes von der nächsten Quadratur, in einem Kreise zum Radius = 1, proportional.[7] Alles dieses unter der Voraussetzung, dass die Variation in den Octanten von mittlerer Grösse sei. Ist sie daselbst grösser oder kleiner, so muss dieser Sinus versus in demselben Verhältniss vergrössert oder verkleinert werden.
§. 31. Aufgabe. Man soll aus der stündlichen Bewegung des Mondes seinen Abstand von der Erde finden.
Die Fläche, welche der Mond in jedem Augenblick um die Erde beschreibt, ist der stündlichen Bewegung desselben und dem Quadrat seines Abstandes von der Erde zusammengesetzt proportional.[8] Folglich steht der Abstand in einem Verhältniss, welches aus dem halben directen Verhältniss der Fläche und dem halben indirecten der stündlichen Bewegung zusammengesetzt ist.
Zusatz 1. Man erhält durch dieses Mittel den scheinbaren Durchmesser des Mondes, indem derselbe sich umgekehrt wie der Abstand von der Erde verhält. Es mögen die Astronomen untersuchen, wie genau diese Regel mit den Erscheinungen übereinstimmt.
Zusatz 2. Man kann, hiernach auch, mittelst der Erscheinungen, die Bahn des Mondes viel genauer als bisher bestimmen.
§. 32. Aufgabe. Man soll die Durchmesser der Bahn bestimmen, in welcher der Mond sich bewegen muss; vorausgesetzt, dass sie keine Excentricität habe.
Die Krümmung der Curve, welche ein beweglicher Körper beschreiben würde, wenn eine Kraft ihn stets nach einer auf erstere perpendikulären Linie anzöge, steht im directen Verhältniss der Anziehung und im indirecten Verhältniss des Quadrats der Geschwindigkeit.[9] Ich setze voraus, dass die Krümmungen der Curve unter einander im letzten Verhältniss der Sinusse oder Tangenten der Berührungswinkel stehen, welche gleichen Radien angehören, im Fall die letzteren unendlich klein werden.
Die Anziehung des Mondes gegen die Erde in den Syzygien ist der Ueberschuss seiner Schwere gegen diese über die Kraft der Sonne = 2PK, welche letztere der Unterschied der Schwere des Mondes und der Erde gegen die Sonne ist. In den Quadraturen ist jene Anziehung gleich der Summe der Schwere des Mondes gegen die Erde und der gegen die Erde gerichteten Sonnenkraft. Setzt man nun = N, so werden diese Anziehungen sehr nahe proportional und oder auch
Wird nämlich die beschleunigende Schwerkraft des Mondes gegen die Erde durch die Zahl 178725 dargestellt, so ist die mittlere Kraft ML, welche in den Quadraturen = PT oder = TK und den Mond gegen die Erde zieht, gleich 1000, und die mittlere Kraft TM in den Syzygien = 3000. Subtrahirt man von der letzteren die mittlere Kraft ML, so bleibt 2000 übrig, womit der Mond sich in den Syzygien von der Erde entfernt und welche ich oben 2 · PK genannt habe.
Die Geschwindigkeit des Mondes in den Syzygien A und B verhält sich zu seiner Geschwindigkeit in den Quadraturen, wie CT : AT, und wie das Moment der Fläche, welches der Mond in den Syzygien um die Erde beschreibt, zu dem Moment derselben Fläche in den Quadraturen, zusammensetzt; also wie
Verbindet man dieses Verhältniss, indirect und doppelt genommen, mit dem obigen 1., direct und einfach genommen; so ist es klar, dass die Krümmung der Mondbahn in den Syzygien sich an ihrer Krümmung in den Quadraturen verhält, wie 120406729 · 178725 · AT² · CT² · N – 120406729 · 2000 AT4 · CT : 122611329 · 178725 AT² · CT² · N + 122611329 · 1000 AT · CT4 d. h. wie
Da die Figur der Mondbahn unbekannt ist, wollen wir voraussetzen, sie sei gleich der Ellipse DBCA, in deren Mittelpunkte T sich die Erde befindet. Ihre grosse Axe DC gehe durch die Quadraturen, ihre kleine Axe AB durch die Syzygien. Da die Ebene dieser Ellipse sich mit einer Winkelbewegung um die Erde dreht, und da die Curve, deren Krümmung wir suchen, in einer von aller Winkelbewegung freien Ebene beschrieben sein soll; so müssen wir die Figur betrachten, welche der Mond in dieser festen Ebene beschreibt, während er seinen Umlauf in dieser Ellipse macht, d. h. die Figur Cpa. Jeder Punkt p der letzteren wird so bestimmt, dass man einen beliebigen Punkt P in der Ellipse annimmt um den Ort des Mondes darzustellen und hierauf Tp = TP so legt, dass der Winkel PTp der scheinbaren Bewegung der Sonne seit der Quadratur C gleich werde, oder (was sehr nahe auf dasselbe hinauskommt), dass CTp : CTP, wie die synodische Umlaufszeit des Mondes zu seiner periodischen, oder
Nimmt man also CTa : CTA (90°) in demselben Verhältniss, und macht man Ta = TA; so ist a die untere und C die obere Apside der Bahn Cpa. Was die Krümmungen in diesen beiden Punkten betrifft, so finde ich nach Ausführung der erforderlichen Rechnung, dass der Unterschied zwischen der Krümmung der Bahn Cpa im Scheitel a und der Krümmung des Kreises zum Mittelpunkt T und Radius TA sich zum Unterschiede zwischen der Krümmung der Ellipse im Scheitel A und der Krümmung desselben Kreises verhält, wie CTP² : CTp². Ferner verhält sich die Krümmung der Ellipse in A zur Krümmung dieses Kreises, wie TA² : TC². Die Krümmung dieses Kreises zur Krümmung desjenigen Kreises, dessen Mittelpunkt T und Radius TC ist, verhält sich wie TC : TA. Ferner verhält sich die Krümmung des letzteren Kreises zur Krümmung der Ellipse in C, wie TA² : TC².
Endlich verhält sich der Unterschied zwischen der Krümmung der Ellipse in C und der Krümmung des letzteren Kreises zum Unterschiede zwischen der Krümmung der Figur Cpa im Scheitel C und der Krümmung des letzteren Kreises, wie CTp² : CTP². Dies findet man leicht aus den Sinussen der Berührungswinkel und der Unterschiede dieser Winkel.[11]
Benutzt man alle diese Verhältnisse, so findet man, dass die Krümmung der Bahn Cpa in a sich zu ihrer Krümmung in C verhält, wie
Die Zahl stellt den Unterschied der Quadrate CTp² – CTP², dividirt durch CTP², oder was dasselbe ist
Da nun a die Syzygie und C die Quadratur des Mondes vorstellt, so muss das eben gefundene Verhältniss dasselbe sein, welches oben in Gl. 3. für die Krümmung der Mondbahn in den Syzygien zur Krümmung in den Quadraturen gefunden worden ist. Um nun das Verhältniss CT : AT zu finden, brauchen wir nur die äusseren und mittleren Glieder der so entstehenden Proportion mit einander zu multipliciren, und erhalten so, nachdem die entstehenden Glieder durch TC · AT dividirt worden sind, folgende Gleichung:
+ 36342 AT² · CT² – 362047 N · AT² · CT + 2191371 N · AT³
+ 4051,4 AT4 = 0.
Setzt man in derselben N = = 1 und = x also CT = 1 + x und AT = 1 – x; so ergibt sich x = 0,00719, also die halbe grosse Axe CT = 1,00719 und die halbe kleine Axe AT = 0,99281 so wie sehr nahe CT : AT = 701/24 : 691/24.
Es verhält sich daher der Abstand des Mondes von der Erde in den Syzygien zum Abstande in den Quadraturen, wie 691/24 : 701/24 oder in runden Zahlen wie 69 : 70; vorausgesetzt, dass man von der Excentricität abstrahire.
§. 33. Aufgabe. Man soll die Variation des Mondes finden.
Diese Ungleichheit des Mondes entsteht zum Theil aus der elliptischen Gestalt seiner Bahn, zum Theil aus der Ungleichheit der Momente der Fläche, welche er um die Erde beschreibt. Setzt man voraus, dass der Mond P (Fig. 193.) sich in einer Ellipse DBCA um die ruhende und im Mittelpunkt derselben befindliche Erde bewege; so wird er Flächen CTP beschreiben, welche den Zeiten proportional sind. Verhält sich ferner die halbe grosse Axe CT der Ellipse zur halben kleinen CA, wie 70 : 69, so wird die Tangente von CTP sich zur Tangente der mittleren Bewegung, letztere von der Quadratur C an gerechnet, sich verhalten wie 69 : 70.[13]
Die Beschreibung der Fläche CTP muss aber, beim Uebergange des Mondes von der Quadratur zur Syzygie beschleunigt werden und zwar so, dass ein Moment in der Syzygie sich zum Moment in der Quadratur verhalte, wie 11073 : 10973 und dass der Ueberschuss des Momentes in irgend einem zwischenliegenden Orte P über das Moment in der Quadratur proportional sei sinCTP² (§. 30.). Dies wird man genau genug ausführen, wenn man tgCTP im Verhältniss = 68,6877 : 69 vermindert. Hierdurch wird tg CTP zur Tangente der mittleren Bewegung, wie 68,6877 : 70,[14] sich verhalten. In den Octanten, wo die mittlere Bewegung = 45° ist, wird daher der Winkel CTP = 44° 27′ 28″, und subtrahirt man diesen von der mittleren Bewegung; so bleibt 32′ 32″ als grösste Variation. Dies würde sich so verhalten, wenn der Mond beim Uebergange von der Quadratur zur Syzygie einen, genau 90° fassenden, Winkel CTA beschriebe. Wegen der Bewegung der Erde aber, vermöge welcher die Sonne in ihrer scheinbaren Bewegung rechtläufig fortgeht, beschreibt der Mond, ehe er die Sonne erreicht, einen Winkel CTa, welcher im Verhältniss der synodischen Umlaufszeit zur periodischen, d. h. im Verhältniss 29d 12h 44m : 27d 7h 43m grösser als 90° ist. Man muss daher alle Winkel um den Mittelpunkt T in demselben Verhältniss vergrössern, wodurch die vorher gefundene grösste Variation von 32′ 32″ nun in 35′ 10″ übergeht.
So gross ist die Variation in der mittleren Entfernung der Sonne Ton der Erde, indem man die Unterschiede vernachlässigt, welche aus der Krümmung der grossen Bahn und aus der verschiedenen Wirkung der Sonne auf den Mond, wenn dieser neu und wachsend, als wenn er voll und abnehmend ist, hervorgehen.
Für die anderen Abstände der Sonne von der Erde steht die grösste Variation in einem Verhältniss, welches aus dem doppelten directen der synodischen Umlaufszeit des Mondes (für eine gegebene Jahreszeit) und dem dreifachen indirecten Verhältniss des Abstandes der Erde von der Sonne zusammengesetzt ist. Im Apogeum der Sonne ist daher die grösste Variation 33′ 14″ und im Perigeum 37′ 11″; vorausgesetzt, dass die Excentricität der Sonne sich zur halben grossen Axe ihrer Bahn verhalte, wie 1615/16 : 1000.
Wir haben bis jetzt die Variation des Mondes unter der Voraussetzung gefunden, dass seine Bahn nicht excentrisch, und dass in den Octanten sein Abstand von des Erde immer der mittlere sei. Da aber der Mond, vermöge seiner Excentricität, der Erde bald näher, bald ferner ist, als in der eben betrachteten Bahn; so kann auch seine Variation etwas grösser oder kleiner als nach der hier angeführten Regel werden. Diese Aenderungen durch Beobachtungen zu bestimmen, überlasse ich den Astronomen.
§. 34. Aufgabe. Man soll die stündliche Bewegung der Mondknoten in einer kreisförmigen Bahn bestimmen.
Es bezeichne S die Sonne, T die Erde, P den Mond, NPn die Mondbahn und Npn dieselbe, auf die Ebene der Ekliptik projicirt. Fener seien N und n die Knoten, nTNm die unbestimmt verlängerte Knotenlinie, PJ sei auf ST, PK auf Qq, Pp auf die Ebene der Ekliptik perpendikulär gefällt. A und B bezeichnen die Syzygien des Mondes, Q und q seine Quadraturen in der Ebene der Ekliptik, AZ sei perpendikulär auf die Knotenlinie Nn gezogen und pK perpendikulär auf die Linie Qq, welche beide Quadraturen verbindet. Die Kraft der Sonne wodurch die Bewegung des Mondes gestört wird, ist (nach §. 29.) aus zwei Kräften zusammengesetzt, von denen die eine LM, die andere der Linie MT, in der Figur jenes Paragraphen, proportional ist.
Durch die erstere wird der Mond gegen die Erde, durch die zweite gegen die Sonne gezogen und zwar längs einer ST parallelen Linie.
Die Kraft LM wirkt längs der Ebene der Mondbahn, und kann daher die Lage derselben nicht ändern; sie braucht deshalb hier nicht betrachtet zu werden. Was die Kraft MT betrifft, durch welche die Ebene der Mondbahn gestört wird, so wird sie durch 3 · PK oder 3 · JT ausgedrückt. Sie verhält sich (nach §. 29.) an derjenigen Kraft, vermöge welcher der Mond sich gleichförmig während seiner periodischen Umlaufszeit um die als ruhend vorausgesetzte Erde bewegen könnte, wie 3 · JT : 178,725 mal den Radius, oder wie JT : 59,575 mal den Radius des Kreises.
Uebrigens nehme ich bei dieser und den folgenden Rechnungen alle vom Monde zur Sonne gesogenen Linien als parallel mit denjenigen an, welche von der Erde zur Sonne gezogen sind. Die Neigung dieser Linien vermindert nämlich in einigen Fällen nahezu alle Wirkungen eben so sehr, als sie dieselben in anderen Fällen vermehrt, und wir suchen hier die mittleren Bewegungen der Knoten, indem wir die unmerklichen kleinen Theile vernachlässigen, durch welche die Rechnung zu verwickelt werden würde.
PM bezeichne nun den Bogen, welchen der Mond in einem gegebenen Zeittheilchen beschreibt und ML die kleine Linie, welche der Mond in derselben Zeit, vermöge der vorher angeführten Kraft 3 · JT zurücklegen könnte. Man ziehe PL und PM, verlängere beide bis l und m, wo sie die Ebene der Ekliptik schneiden; ferner ziehe man aus P das Perpendikel PH auf Tm. Da LM der Ebene der Ekliptik parallel ist, und daher die in dieser Ebene liegende Linie lm nicht schneiden kann; da ferner beide Linien ML und ml in derselben Ebene LMPml liegen: so müssen sie einander parallel und daher Δ LMP ∼ lmP sein. Nun liegt MPm in der Ebene der Bahn, in welcher sich der Mond in P bewegt, daher wird der Punkt m auf die Linie Nn fallen, welche durch die Knoten N,n dieser Bahn gezogen ist. Ferner würde die Kraft, welche die Beschreibung von ½LM bewirkt, in derselben Zeit die Beschreibung dieser ganzen Linie LM herbeiführen, wenn sie auf einmal im Orte P ganz angebracht wäre. Sie würde daher den Mond zwingen, sich auf dem zur Sehne LP gehörigen Bogen zu bewegen; der Mond würde daher aus der Ebene MPmT in die Ebene LPlT gebracht und die durch diese Kraft erzeugte Winkelbewegung der Knoten dem Winkel mTl gleich sein. Nun ist ml : mP = ML : MP, also, weil MP durch die Voraussetzung einer constanten Zeit gegeben ist, ml proportional dem Rechteck ML · mP, d. h. JT · mP.
Setzt man nun Tml = 90°, so wird mTl proportional also auch proportional ; oder, was auf dasselbe hinauskommt (weil Tm : mP = TP : PH), der Winkel mTl proportional oder JT · PH, weil TP gegeben ist.
Da aber der Winkel Tml oder STN nicht = 90° ist, so wird mTl kleiner und zwar im Verhältniss von sin STN zum Radius oder dem AZ : AT.
Die Geschwindigkeit der Knoten wird demnach proportional JT · PH · AZ, oder dem Produkt sin TPJ · sin PTN · sin STN.
Befinden sich die Knoten in den Quadraturen und der Mond in den Syzygien, so sind diese Winkel = 90°; alsdann liegt die kleine Linie ml in unendlicher Entfernung, und es wird mTl = mPl.
Im diesem Falle verhält sich der Winkel mPl zu PTM, welchen der Mond während derselben Zeit in seiner scheinbaren Bewegung um die Erde beschreibt, wie 1 : 59,575.
Der Winkel mPl ist nämlich = LPM, d. h. = dem Winkel, um welchen der Mond vom geradlinigen Wege abgebracht wird, und welcher in dieser gegebenen Zeit durch die Sonnenkraft 3 · JT allein hervorgebracht werden würde, wenn der Mond aufhörte, schwer zu sein. Ferner ist PTM gleich dem Winkel, um welchen der Mond vom gradlinigem Wege durch diejenige Kraft allein, welche ihn in seiner Bahn erhält, abgebracht wird, indem man von der Sonnenkraft 3 · JT abstrahirt. Diese Kräfte verhalten sich zu einander, nach dem oben Gesagten, wie 1 : 59,575.
Da nun die stündliche mittlere Bewegung des Mondes, in Bezug auf die Fixsterne 32′ 56″,5 beträgt, so wird die stündliche Bewegung des Knotens in diesem Falle 33″,2.
In anderen Fällen wird sich die stündliche Bewegung der Knoten zur grössten 33″,2 verhalten, wie das Produkt sin TPJ · sin PTN · sin STN zum Cubus des Radius. Der Winkel TPJ bezeichnet den Abstand des Mondes von der Quadratur, PTN den Abstand des Mondes vom Knoten und STN den Abstand des Knotens von der Sonne.
So oft das Zeichen eines dieser Winkel vom Positiven zum Negativen, oder umgekehrt vom Negativen zum Positiven übergeht, wird die Bewegung der Knoten aus einer rückgängigen in eine rechtläufige und umgekehrt übergehen. Hiervon rührt es her, dass die Knoten allemal vorwärtsschreiten, wenn der Mond sich zwischen einer der Quadraturen und dem ihr am nächsten liegenden Knoten befindet. In den anderen Fällen gehen die Knoten rückwärts und vermöge des Ueberschusses der rückläufigen Bewegung über die rechtläufige, werden die Knoten in jedem Monat in rückläufiger Richtung fortbewegt.
Zusatz 1. Man fälle aus den Endpunkten P und M eines gegebenen unendlich kleinen Bogens PM auf die, durch die Quadraturen Q und q gehende Linie Qq die Perpendikel PK und Mk und verlängere dieselben, bis sie die Knotenlinie Nn in D und d schneiden. Alsdann wird die stündliche Bewegung der Knoten, der Fläche MPDd und dem Quadrat der Linie AZ zusammen gekommen, proportional sein.
Es seien PK, PH, AZ die drei Sinusse, von denen die Rede gewesen ist, nämlich PK der Sinus des Winkelabstandes des Mondes von der Quadratur, PH der Sinus seines Abstandes vom Knoten, AZ der Sinus des Abstandes des Knotens von der Sonne; alsdann ist die Geschwindigkeit des Knotens proportional,
Nun ist aber PT : PK = PM : Kk, also, weil PT und PM gegeben sind,
Ferner haben wir AT : PD = AZ : PH, also ist
Mittelst 2. und 3. wird daher PK · PH · AZ proportional Kk · PD · AZ², d. h. der Fläche PDdM und AZ² zusammengenommen. W. z. b. w.
Zusatz 2. In einer beliebigen gegebenen Lage der Knoten verhält sich ihre mittlere stündliche Bewegung zur Hälfte der stündlichen Bewegung in den Syzygien des Mondes, d. h. zu 16″,6, wie das Quadrat vom Sinus des Winkelabstandes der Knoten von den Syzygien zum Quadrat des Radius, oder wie AZ² : AT².
Durchläuft nämlich der Mond mit gleichförmiger Bewegung den Halbkreis QAq, so wird die Summe aller während der Zeit, wo der Mond von Q bis M gelangt, beschriebenen Flächen PDdM gleich sein der Fläche QMdE, welche durch die Tangente QE des Kreises begrenzt ist. Ferner wird die Summe aller PDdM, während der Mond bis n gelangt, der Fläche EQAn gleich sein, welche die Linie PD beschreibt. Geht hierauf der Mond weiter von n bis q, so fällt die Linie PD ausserhalb des Kreises und beschreibt die Fläche nqe, welche durch die Tangente eq des Kreises begrenzt ist. Diese Fläche wird, weil die Knoten anfangs rückwärts und hierauf vorwärts schreiten, von der ersteren Fläche abgezogen, und es wird, weil eqn = EQN, der Rest dem Halbkreise NQAn gleich. Die Summe aller Flächen PDdM, welche während der Zeit, wo der Mond einen Halbkreis durchläuft, beschrieben sind, wird also gleich der Fläche des Halbkreises. Die Summe aller derselben Flächen, welche während der Zeit beschrieben sind, wo der Mond den ganzen Kreis durchläuft, ist der Fläche des ganzen Kreises gleich.
Befindet sich aber der Mond in den Syzygien, so ist die Fläche PDdM gleich dem Rechteck unter dem Bogen PM und dem Radius PT. Die Summe aller ihr gleichen Flächen, welche in der Zeit beschrieben werden, während der Mond den Kreis durchläuft, ist gleich dem Rechteck über der ganzen Peripherie und dem Radius. Dieses Rechteck ist noch einmal so gross, als ein Kreis, also als das vorhergehende Rechteck. Die Knoten würden also mit einer gleichförmigen Geschwindigkeit, welche derjenigen gleich ist, die sie in den Syzygien haben, einen doppelt so grossen Raum beschreiben, als derjenige, welchen sie wirklich zurücklegen. Die mittlere gleichförmige Bewegung, womit die Knoten denselben Raum zurücklegen würden, den sie mit ungleichförmiger Bewegung wirklich durchlaufen, ist daher gleich der Hälfte derjenigen Bewegung, welche sie in den Syzygien des Mondes haben. Nun ist die grösste stündliche Bewegung, im Fall die Knoten sich in den Quadraturen befinden = 33″,2, und die mittlere stündliche Bewegung in diesem Falle = 16″,6.
Die stündliche Bewegung der Knoten ist aber stets dem Produkt AZ² · PDdM proportional und dies ist auch noch der Fall, wenn sie in den Syzygien sind, oder auch in diesem Falle allein AZ², (weil alsdann die Fläche PDdM gegeben ist). Die mittlere stündliche Bewegung wird ebenfalls AZ² proportional und, im Fall die Knoten ausserhalb der Quadraturen liegen, sich zu 16″,6 verhalten, wie AZ² : AT². W. z. b. w.
§. 35. Aufgabe. Man soll die stündliche Bewegung der Mondknoten in einer elliptischen Bahn finden.
Qpmaq bezeichne eine Ellipse, Qq ihre grosse und ab ihre kleine Axe. QAqB sei ein umschriebener Kreis, T die im gemeinschaftlichen Mittelpunkte der Ellipse und des Kreises befindliche Erde, S die Sonne, p der auf der Ellipse sich bewegende Mond, pm der Bogen, welchen er in einem gegebenen unendlich kleinen Zeittheilchen beschreibt. Ferner sei Nn die Linie, welche die Knoten N und n verbindet, pK und mk Perpendikel, welche auf die Axe Qq gefällt und so weit verlängert sind, bis sie den Kreis in P und M, und die Knotenlinie in D und d schneiden. Wenn nun der Mond um die Erde der Zeit proportionale Flächen beschreibt, so wird die stündliche Bewegung des Knotens in der Ellipse der Fläche pDdm und AZ² zusammengenommen proportional sein.
Um dies zu beweisen, ziehe man PF und pf, welche den Kreis und die Ellipse respective in P und p berühren und die Knotenlinie Nn in F und f, einander und die Axe TQ aber in Y schneiden. Es werde ML genommen, um dadurch den Weg zu bezeichnen, welchen der Mond, wenn er sich auf dem Kreise bewegte, in transversaler Richtung vermöge der Kraft 3JT oder 3 · PK, in der Zeit beschreiben könnte, während er den Bogen PM zurücklegt. Man nehme ferner ml als den Weg an, welchen der Mond bei seiner Bewegung auf der Ellipse, in derselben Zeit und vermöge derselben Kraft zurücklegen würde. Hierauf verlängere man LP und lp, bis sie die Ebene der Ekliptik in G und g schneiden und ziehe FG und fg, von denen die erstere, verlängert, die Linien pf, pg und TQ respective in c, e und R, die zweite die Linie TQ in r schneidet.
Es ist klar, dass die Kraft 3 · JT oder 3 · PK im Kreise sich zur Kraft 3 · JT oder 3 · pK in der Ellipse verhält, wie
Ferner verhält sich der, vermöge der ersteren Kraft beschriebene Weg ML zu dem, vermöge der letzteren Kraft beschriebenen Wege ml, wie PK : pk, d. h. weil PYKp ∼ FYRc,
Da aber Δ PLM ∼ PGF, so wird ML : FG = PL : PG d. h. ML : FG = pl : pe (weil Lk ∥ PK ∥ GR) ML : FG = lm : ce (weil Δ plm ∼ pce), und es wird mithin
Wenn demnach fg : ce = fY : cY = fr : cR, d. h. wenn fg : ce = so erhält man, indem man die letzte Proportion mit der identischen ce : FG = ce : FG verbindet,
Die Winkel an der Erde T, welche durch fg und FG unterspannt würden, wären also einander gleich. Diese Winkel sind aber nach dem, was wir im vorhergehenden Paragraphen gesehen haben, die Bewegungen der Knoten während der Zeit, wo der Mond die Bogen PM und pm respective auf dem Kreise und der Ellipse zurücklegt und daher die Bewegungen der Knoten auf beiden einander gleich.
Dies würde in der That so sein, wenn fg : ce = fY : cY also
Da aber Δ fgp ∼ cep, so hat man fg : ce = fp : cp also
folglich wird der von fg unterspannte Winkel sich zu denjenigen verhalten, welchen FG unterspannt, d. h. es verhält sich die Bewegung der Knoten in der Ellipse zu der ihr im Kreise entsprechenden, wie das fg in 6. zu dem früheren in 5., oder wie
d. h. zusammengesetzt wie
und |
8. | . |
Nach §. 34., Zusatz 1. steht nun die stündliche Bewegung der Knoten im Kreise im zusammengesetzten Verhältniss von AZ² und DPMd; mithin ist die stündliche Bewegung der Knoten in der Ellipse AZ² und Dpmd zusammengesetzt proportional. W. z. b. w.
Zusatz 1. Für eine gegebene Lage der Knoten wird die Summe aller Flächen pDdm, welche während der Zeit beschrieben sind, wo der Mond von der Quadratur bis zu einem beliebigen Punkte m fortgeht, gleich der Fläche mpQEd, welche durch die Tangente QE an der Ellipse begrenzt wird. Die Summe aller dieser, während eines ganzen Umlaufs des Mondes beschriebenen Flächen, wird der ganzen elliptischen Fläche gleich. Ferner verhält sich die mittlere Bewegung der Knoten auf der Ellipse zur entsprechenden auf dem Kreise, wie die Ellipse zum Kreise, d. h. wie Ta : TA, oder wie 69 : 70.
Da nun (nach §. 34., Zusatz 2.) die mittlere stündliche Bewegung der Knoten beim Kreise sich zu 16″,6 verhält wie AZ² : AT², so nehme man 16″,4 : 16″,6 = 69 : 70, und es wird sich alsdann die mittlere stündliche Bewegung der Knoten auf der Ellipse zu 16″,4 verhalten, wie AZ² : AT², d. h. wie das Quadrat vom Sinus des Winkelabstandes des Knotens von der Sonne zum Quadrat des Radius.
Uebrigens werden die vom Monde um die Erde beschriebenen Flächen schneller in den Syzygien, als in den Quadraturen durchlaufen, und die Zeit muss daher in den Syzygien kürzer, in den Quadraturen hingegen länger werden. Die Bewegung der Knoten wird aber dasselbe Gesetz beobachten. Nun verhält sich das Moment der Fläche in den Quadraturen des Mondes zum Moment in den Syzygien, wie 10973 : 11073 (§. 30.); folglich verhält sich das mittlere Moment in den Octanten zum Ueberschuss in den Syzygien und zum Mangel in den Quadraturen, wie die halbe Summe dieser Zahlen zu ihrer halben Differenz, d. h. wie 11023 : 50.
Die Zeit gleicher Theile der Mondbahn verhält sich aber umgekehrt, wie die Geschwindigkeit, und die mittlere Zeit in den Octanten verhält sich daher zum Ueberschuss der Zeiten in den Quadraturen und zum Mangel in den Syzygien, welche beide durch diese Ursache hervorgebracht werden, sehr nahe, wie 11023 : 50.[16]
Geht man von den Quadraturen zu den Syzygien fort, so finde ich, dass der Ueberschuss der Momente der Fläche in den einzelnen Orten über das kleinste Moment in den Quadraturen sehr nahe dem Quadrat vom Sinus des Winkelabstandes des Mondes von den Quadraturen proportional ist (§. 30., Bem.242). Folglich wird der Unterschied zwischen dem Moment an einem beliebigen Orte und dem mittleren Momente in den Octanten proportional sein dem Unterschiede zwischen dem Quadrate vom Sinus des Winkelabstandes von den Quadraturen und sin 45°² = ½ Radius. Das Increment der Zeit in jedem, zwischen den Quadraturen und Octanten, und ihr Decrement in jedem, zwischen den Octanten und Syzygien gelegenen Orte, wird in demselben Verhältniss stehen. Die Bewegung der Knoten während der Zeit, wo der Mond einzelne gleiche Theile seiner Bahn zurücklegt, wird im doppelten Verhältniss der Zeit beschleunigt oder verzögert. Diese Bewegung ist nämlich, während der Mond den Bogen PM durchläuft (unter übrigens gleichen Umständen) ML, ML aber dem Quadrat der Zeit proportional.[17] Daher wird die Bewegung der Knoten in den Syzygien während der Zeit, dass der Mond gegebene Theile seiner Bahn zurücklegt im Verhältniss 11073² : 11023² vermindert. Ferner verhält sich das Decrement zur übrig bleibenden Bewegung wie 100 : 10973 und zur ganzen Bewegung wie 100 : 11073 beiläufig.[18]
Es steht nun das Decrement in den, zwischen den Octanten und Syzygien und das Increment in den, zwischen den Octanten und Quadraturen gelegenen Orten sehr nahe zu diesem Decrement in einem Verhältniss, welches aus dem Verhältniss der ganzen Bewegung in diesen Orten zur ganzen Bewegung in den Syzygien und aus dem Verhältniss zusammengesetzt ist, in welchem der Unterschied zwischen dem Quadrat vom Sinus des Winkelabstandes des Mondes von der Quadratur und dem halben Quadrat des Radius zum letzteren halben Quadrat steht.[19] Befinden sich also die Knoten in den Quadraturen, und nimmt man zwei gleichweit von den Octanten abstehende Orte, und ausserdem zwei andere an, welche eben so weit von der Syzygie und Quadratur entfernt sind; zieht man hierauf von den Decrementen der Bewegungen in den beiden, zwischen der Syzygie und dem Octanten gelegenen Orten, die Incremente der Bewegungen in den beiden anderen, zwischen Octant und Quadratur gelegenen, Orten ab: so wird der Rest dem Decrement in der Syzygie gleich sein. Hiervon ist der Grund leicht einzusehen.[20] Es ergibt sich demnach hieraus, dass das mittlere Decrement, welches von der mittleren Bewegung der Knoten abgezogen werden muss, dem vierten Theile des Decrementes in der Syzygie gleich ist. Die ganze stündliche Bewegung der Knoten in den Syzygien ist, unter der Voraussetzung, dass der Mond den Zeiten proportionale Flächen um die Erde beschreibe, nach dem früher Gefundenen = 32″,7. Ferner verhält sich das Decrement der Knotenbewegung während der Zeit, wo der Mond denselben Weg geschwinder zurücklegt, zu eben dieser Bewegung, wie 100 : 11073. Das Decrement ist daher = 0″,3 und zieht man dessen vierten Theil = 0″,1 von der früher gefundenen mittleren stündlichen Bewegung 16″,4 ab; so erhält man die verbesserte stündliche Bewegung = 16″,3.
Befinden sich die Knoten ausserhalb der Quadraturen und betrachtet man zwei, auf beiden Seiten gleichweit von den Syzygien abstehende Orte; so wird die Summe der Knotenbewegungen, wenn der Mond sich in diesen Orten befindet, zur entsprechenden Summe der Bewegungen für den Fall, dass die Knoten in den Quadraturen liegen, sich verhalten, wie AZ² : AT². Ferner werden die, aus den eben besprochenen Ursachen hervorgehenden, Decremente der Bewegungen sich wie die letzteren verhalten, d. h. die übrig bleibenden Bewegungen verhalten sich zu einander, wie AZ² : AT² und die mittleren Bewegungen sind den übrig bleibenden proportional. Die verbesserte mittlere stündliche Bewegung, in einer beliebig gegebenen Lage der Knoten, verhält sich daher zu 16″,3, wie AZ² : AT², d. h. wie das Quadrat vom Sinus des Winkelabstandes der Knoten von den Syzygien zum Quadrat des Radius.
§. 36. Aufgabe. Man soll die mittlere jährliche Bewegung der Mondknoten finden.
Die mittlere jährliche Bewegung ist gleich der Summe aller mittleren stündlichen Bewegungen im Jahre. Man denke sich nun, dass der Knoten sich in N befinde und am Ende jeder Stunde an seinen ersten Ort zurückversetzt werde; so dass er, ungeachtet seiner eigenen Bewegung, immer dieselbe Lage in Bezug auf die Fixsterne beibehalte. Ferner setze man voraus, dass während dieser Zeit die Sonne S, vermöge der Bewegung der Erde, sich von diesem Knoten entferne und ihren jährlichen scheinbaren Umlauf gleichförmig vollende. Aa sei ein sehr kleiner gegebener Bogen, welchen die nach der Sonne gezogene Linie TS, in einer gegebenen sehr kleinen Zeit, auf dem Kreise NAn durchläuft. Die mittlere stündliche Bewegung wird alsdann nach dem, was wir oben gezeigt haben, AZ², d. h. weil AZ und ZY einander proportional sind[21] dem Rechteck AZ · ZY oder der Fläche AZYa proportional sein. Die Summe aller mittleren stündlichen Bewegungen vom Anfang an wird der Summe aller Flächen AZYa, d. h. der Fläche NAZ proportional sein. Nun ist die grösste Fläche AZYa gleich dem Rechteck unter dem Bogen Aa und dem Radius des Kreises, folglich wird sich die Summe aller Rechtecke im ganzen Kreise zur Summe eben so vieler grösster Rechtecke verhalten, wie die Fläche des ganzen Kreises zum Rechteck unter der ganzen Peripherie und dem Radius, d. h. wie 1 : 2.
Die stündliche Bewegung, welche dem grössten Rechtecke entspricht, war aber = 16″,3 gefunden worden, und ihre Summe für ein ganzes siderisches Jahr von 365d 6h 9m wird daher = 39° 38′ 7″,8. Die Hälfte der letzteren, oder 19° 49′ 3″,9 ist die mittlere Bewegung der Knoten, welche dem ganzen Kreise entspricht. Ferner wird die Bewegung der Knoten, während die Sonne von N bis A fortschreitet, sich zu 19° 49′ 3″,9 verhalten, wie die Fläche NAZ zum ganzen Kreise.
Dies würde sieh eo unter der Voraussetzung verhalten, dass der Knoten nach Jeder einzelnen Stunde an seinen früheren Ort zurückgebracht würde und dass die Sonne am Ende eines Jahres zu demselben Knoten zurückkehrte, von welchem sie beim Anfange desselben ausgegangen war. Da aber die Bewegung des Knotens bewirkt, dass die Sonne früher zu ihm zurückkehrt; so muss man berechnen, um wieviel die Zeit der Rückkehr hierdurch verkürzt wird.
Die Sonne legt im Jahre 360°, und der Knoten mit seiner grössten Geschwindigkeit in derselben Zeit 39° 38′ 7″,8 = 39°,6355 zurück; ferner verhält sich die mittlere Bewegung dieses Knotens in dem beliebigen Orte N zu seiner mittleren Bewegung in den Quadraturen, wie AZ² : AT². Die Bewegung der Sonne wird sich daher zur Bewegung des Knotens im Orte N verhalten, wie 360 · AT² : 39,6355AZ² = 9,0827667AT² : AZ².[22]
Setzt man also voraus, dass die ganze Peripherie des Kreises NAn in kleine gleiche Theile Aa getheilt sei; so wird die Zeit, während welcher die Sonne den kleinen Theil Aa durchlaufen würde, im Fall der Kreis sich in Ruhe befände, zu der Zeit, in welcher sie denselben kleinen Theil durchlaufen würde, wenn der Kreis zugleich mit den Knoten sich um den Mittelpunkt T bewegte, sich umgekehrt verhalten wie 9,0827667 · AT² : 9,0827667 · AT² + AZ².
Die Zeit verhält sich nämlich umgekehrt wie die Geschwindigkeit, mit welcher dieser kleine Theil durchlaufen wird und diese Geschwindigkeit ist der Summe der Geschwindigkeiten von Sonne und Knoten gleich. Es werde daher die Zeit, in welcher die Sonne, ohne die Bewegung des Knotens, den Bogen NA durchlaufen würde, durch den Sector NTA dargestellt. Ferner stelle der kleine Theil ATa dieses Sectors das kleine Zeittheilchen dar, während dessen der sehr kleine Bogen Aa durchlaufen werden würde. Man fälle aY perpendikulär auf Nn und nehme dZ auf Az so gross an, dass dZ · ZY : ATa = AZ² : αAT² + AZ² (α = 9,0827667) d. h. dZ : ½AZ = AT² : α · AT² + AZ²; alsdann wird das Rechteck dZ · ZY das Decrement der Zeit darstellen, welches die Bewegung des Knotens während der ganzen Zeit, wo der Bogen Aa durchlaufen wird, hervorbringt. Ist ferner die Curve NdGn der Ort der Punkte d, so stellt die krummlinige Fläche NdZ das ganze Decrement während der Zeit, welche zur Durchlaufung des Bogens NA gebraucht wird, dar. Endlich ist der Ueberschuss des Sectors NAT über die Fliehe NdZ diese ganze Zeit.[23] Da nun die Bewegung des Knotens während einer kürzeren Zeit, im Verhältniss der letzteren kleiner ist; so muss die Fläche AaYZ in demselben Verhältniss verkleinert werden. Dies wird geschehen, indem man auf AZ die Linie eZ so annimmt, dass eZ : AZ = AZ² : αAT² + AZ². Hiernach wird das Rechteck eZ · ZY sich zur Fläche AZYa verhalten, wie das Decrement der Zeit, welches zur Durchlaufung des Bogens Aa erforderlich war, zu der ganzen Zeit, in welcher er bei ruhendem Knoten würde durchlaufen worden sein. Folglich wird dieses Rechteck dem Decrement der Bewegung des Knotens entsprechen. Ist nun die Curve NeFn der Ort der Punkte e, so wird die ganze Fläche NeZ, welche der Summe aller Decremente gleich ist, dem ganzen Decrement während der zur Durchlaufung des Bogens NA erforderlichen Zeit entsprechen. Die übrig bleibende Fläche NAe wird der übrig bleibenden Bewegung entsprechen, welche die wahre Bewegung des Knotens während der Zeit ist, wo der ganze Bogen NA durch die vereinigten Bewegungen der Sonne und der Knoten beschrieben wird.[24]
Wendet man nun die Methode der unendlichen Reihen an, so findet man, dass der Flächeninhalt des Halbkreises sich zu dem Inhalt der gesuchten Figur NeFn sehr nahe verhält, wie 793 : 60.[25]
Da nun die, dem ganzen Kreise entsprechende, Bewegung = 19° 49′ 3″,9 war, so wird die, dem Doppelten der Figur NeFn, entsprechende, Bewegung = 1° 29′ 58″,0.
Subtrahirt man diese von der ersten Bewegung, so erhält man 18° 19′ 5″,9 für die ganze Bewegung des Knotens, in Bezug auf die Fixsterne und zwischen zweien seiner Conjunctionen mit der Sonne. Subtrahirt man hierauf diese Bewegung von der jährlichen Bewegung der Sonne, welche = 360° ist; so ergiebt sich die Bewegung der letzteren zwischen denselben beiden Conjunctionen = 341° 40′ 54″,1. Diese verhält sich zur jährlichen Bewegung von 360°, wie die vorher = 18° 19′ 5″,9 gefundene Bewegung des Knotens zur jährlichen Bewegung des letzteren. Diese wird folglich = 19° 18′ 1″,4, und dies ist die mittlere Bewegung der Knoten in einem siderischen Jahre. Für dieselbe hat man nach den astronomischen Tafeln 19° 21′ 21″,8, und der Unterschied, welcher wahrscheinlich von der Excentricität der Mondbahn und ihrer Neigung gegen die Ebene der Ekliptik herrührt, beträgt weniger als 1/300 der ganzen Bewegung.
Durch die Excentricität wird die Bewegung der Knoten etwas beschleunigt, durch die Neigung hingegen etwas verzögert, wodurch sie sehr nahe auf die richtige Grösse zurückkommt.
§. 37. Aufgabe. Man soll die wahre Bewegung der Mondsknoten finden.
Wird die Zeit durch die Fläche NTA – NdZ (Fig. 197.) ausgedrückt, so stellt die Fläche NAe die wahre Bewegung dar, welche man also durch Quadratur findet. Die Rechnung würde aber nach dieser Methode zu mühsam sein, und es ist daher besser, sich der folgenden Construction zu bedienen.
Aus dem Mittelpunkte C werde mit einem beliebigen Radius CD der Kreis BEFD beschrieben und CD so bis A verlängert, dass AB sich zu AC verhalte, wie die mittlere Bewegung zur Hälfte der wahren, wenn die Knoten sich in den Quadraturen befinden; also AB : AC = 19° 18′ 1″,4 : 19° 49′ 3″,9. Es wird daher hieraus BC : AC = 0° 31′ 2″,5 : 19° 49′ 3″,9 = 1 : 38,3. Hierauf ziehe man durch den Punkt D die unbestimmte Linie Gg, welche den Kreis in D berührt, und nehme den Würfel BCE oder BCF gleich dem doppelten Winkelabstande der Sonne von dem Knoten, welchen man durch die mittlere Bewegung findet. Endlich ziehe man AE oder AF, welche das Perpendikel DG in G schneiden, und nehme einen Winkel an, welcher sich zur ganzen Bewegung des Knotens zwischen seinen Syzygien (d. h. zu 9° 11′ 3″) verhält, wie die Tangente DG zur ganzen Peripherie des Kreises BED. Diesen Winkel (für welchen man den Winkel DAG annehmen kann) addire man zur mittleren Bewegung der Knoten, wenn sie von den Quadraturen zu den Syzygien, und subtrahire ihn von derselben, wenn sie von den Syzygien zu den Quadraturen übergehen und man wird ihre wahre Bewegung erhalten. Die so gefundene wahre Bewegung stimmt nämlich sehr nahe mit derjenigen überein, welche man erhalten würde, wenn man wie früher die Zeit durch die Fläche NTA – NdZ und die Bewegung des Knotens durch die Fläche NAe ausdrückte. Hiervon kann man sich durch Rechnung überzeugen.
Dies ist die halbjährige Bewegung der Knoten. Es gibt noch eine Gleichung dieser Bewegung für jeden Monat, allein man bedarf dieser nicht nothwendig, um die Breite des Mondes zu finden. Die Aenderung der Neigung der Mondsbahn gegen die Ekliptik unterliegt nämlich einer doppelten Ungleichheit, einer sechsmonatlichen und einer monatlichen. Die letztere und die Gleichung der Knoten für jeden Monat gleichen sich einander aus und verbessern sich gegenseitig so, dass man sie bei der Bestimmung der Breite des Mondes vernachlässigen kann.
Zusatz. Durch diesen und den vorhergehenden Paragraphen wird es klar, dass die Knoten in ihren Syzygien ruhen, dass sie in ihren Quadraturen mit einer stündlichen Bewegung von 16″,3 zurückgehen und dass die Gleichung der Bewegung in den Octanten 1° 30′ beträgt. Dies stimmt sehr gut mit den Erscheinungen am Himmel überein.
Anmerkung 1. J. Machin, Professor der Astronomie in Grasham und Heinrich Pemberton M. D, haben, jeder für sich, die Bewegung der Knoten nach einer, von der vorhergehenden verschiedenen, Methode gefunden und dieselbe bekannt gemacht. Die Schrift von Dr. Machin, welche zuerst in meinen Besitz gekommen ist, werde ich hier hinzufügen.
Erster Satz. Die mittlere Bewegung der Sonne vom Knoten ab findet man, indem man die mittlere geometrische Proportionale zwischen der mittleren Bewegung der Sonne selbst und derjenigen mittleren Bewegung bestimmt, mit welcher sich die Sonne am geschwindesten vom Knoten in den Quadraturen entfernt.
Es sei T der Ort der Erde, Nn die Knotenlinie des Mondes zu einer beliebigen gegebenen Zeit, KTM eine hierauf perpendikulär gezogene Linie. Ferner sei TA eine Linie, welche sich um den Mittelpunkt mit derselben Winkelgeschwindigkeit dreht, mit welcher die Sonne und der Knoten sich von einander entfernen. Hiernach wird der, zwischen der ruhenden Linie Nn und der sich drehenden AT gebildete, Winkel immer dem Winkelabstande der Sonne vom Knoten gleich sein. Dies vorausgesetzt, theile man die beliebige Linie TK in solche zwei Theile TS und SK dass sie respective der mittleren stündlichen Bewegung der Sonne und der mittleren stündlichen Bewegung des Knotens in den Quadraturen proportional werden. Man nehme ferner
alsdann wird TH der mittleren Bewegung der Sonne vom Knoten ab proportional.
Es werde aus dem Mittelpunkte T mit dem Radius TK der Kreis NKnM beschrieben. Zu demselben Mittelpunkt und den halben Axen TH und TN construire man hierauf die Ellipse HNLn. Wenn man sich nun während der Zeit, wo die Sonne sich vom Knoten um den beliebig grossen Bogen Na entfernt, eine Linie Tba denkt, welche stets durch den Endpunkt a dieses Bogens geht; so wird die Fläche des Sectors NTa die Summe der Bewegungen der Sonne und des Knotens während derselben Zeit darstellen. Es sei Aa der sehr kleine Bogen, welchen die Linie Tba auf diese Weise beschreibt, indem sie sich während eines gegebenen Zeittheilchens gleichförmig umdreht; alsdann wird der kleine Sector ATa der Summe der Geschwindigkeiten proportional sein, womit die Sonne und der Knoten sich während dieses Zeittheilchens fortbewegen. Die Geschwindigkeit der Sonne ist fast gleichförmig, so dass ihre kleine Ungleichheit keine merkliche Aenderung in der mittleren Bewegung der Knoten hervorbringt. Der andere Theil dieser Summe, d. h. die Geschwindigkeit des Knotens in ihrer mittleren Grösse, nimmt mit der Entfernung von den Syzygien im doppelten Verhältniss des Sinus seines Winkelabstandes von der Sonne zu (nach §. 35., Zusatz des dritten Buches der Principien). Da sie nun am grössten in den Quadraturen mit der Sonne in K ist, so hat sie zur Geschwindigkeit der Sonne das Verhältniss wie SK : ST, d. h. wie TK² – HT² : HT² oder wie
Die Ellipse NBHn theilt aber den Sector ATa, welcher die Summe dieser beiden Geschwindigkeiten ausdrückt, in die zwei Theile ABba und BTb, welche eben diesen Geschwindigkeiten proportional sind. Man verlängere nämlich die Linie BT, bis sie den Kreis in β schneidet, ziehe hierauf durch B das Perpendikel BG auf die grosse Axe, welches beiderseits verlängert den Kreis in F und f schneiden wird und man sieht alsdann, dass
Dieses Verhältniss wird aber, wenn der Raum ABba der grösste in K ist, in
übergehen; die grösste mittlere Geschwindigkeit des Knotens steht aber zur Geschwindigkeit der Sonne (nach 2.) in diesem Verhältniss. Der Sector ATa wird daher in den Quadraturen in zwei Theile zerlegt, welche den Geschwindigkeiten proportional sind.
Da nun
und
so wird die kleine Fläche ABba, wenn sie in K am grössten ist, sich zum übrig bleibenden Sector BTb verhalten, wie
Das Verhältniss dieser kleinen Fläche zum übrig bleibenden Sector ist aber (nach 3.) im allgemeinen AB · Bβ : BT²; daher wird die Fläche ABba im Orte A kleiner, als die ihr in den Quadraturen entsprechende, im Verhältniss
d. h. im doppelten Verhältniss vom Sinus des Winkelabstandes zwischen Sonne und Knoten. Ferner wird die Summe aller kleinen Flächen ABba, d. h. die Fläche ABN der Bewegung des Knotens während der Zeit, wo die Sonne sich um den Bogen NA vom Knoten entfernt, proportional sein. Der übrig bleibende Raum, nämlich der elliptische Sector NTB ist der mittleren Bewegung der Sonne, während derselben Zeit, proportional. Da nun die mittlere jährliche Bewegung des Knotens diejenige ist, welche während der Zeit stattfindet, wo die Sonne ihren Umlauf vollendet; so wird die mittlere Bewegung des Knotens von der Sonne sich zur mittleren Bewegung der letzteren verhalten, wie die Kreisfläche zur elliptischen, d. h. wie TK : TH, oder weil nach 1. TH² = TS · TK, wie
Zweiter Satz. Die mittlere Bewegung der Mondsknoten ist gegeben; man soll ihre wahre Bewegung finden.
Es sei der Winkel A der Abstand der Sonne vom mittleren Orte des Knotens, oder die mittlere Bewegung der Sonne vom Knoten ab. Man nehme den Winkel B so an, dass man habe
d. h. im halben Verhältniss der mittleren stündlichen Bewegung der Sonne zu ihrer mittleren stündlichen Bewegung von dem in den Quadraturen befindlichen Knoten ab.[28] Alsdann wird der Winkel B der Abstand der Sonne vom wahren Orte des Knotens sein. Zieht man nämlich FT, so wird der Winkel FTN, nach dem Beweise des vorhergehenden Satzes, der Abstand der Sonne vom mittleren Orte des Knotens, der Winkel ATN ihr Abstand vom wahren Orte sein und
Zusatz. Der Winkel FTA ist also die Gleichung der Mondknoten, und der Sinus dieses Winkels, wenn er in den Octanten am grössten ist, verhält sich zum Radius, wie KH : TK + TH. In einem anderen beliebigen Orte A verhält sich der Sinus dieser Gleichung zum grössten Sinus, wie sin (FTN + ATN) : Radius, d. h. fast wie
oder wie der Sinus des doppelten Winkelabstandes der Sonne vom mittleren Orte des Knotens zum Radius.[29]
Anmerkung. Ist die mittlere stündliche Bewegung der Knoten in den Quadraturen = 16″,3, d. h. in einem ganzen siderischen Jahre = 39° 38′ 7″,8; so hat man TH : TK = = 18,6524761 : 19,6524761 ferner
d. h. wie die Bewegung der Sonne in einem siderischen Jahre zur mittleren Bewegung des Knotens = = 19° 18′ 1″,4.
Wenn aber die mittlere Bewegung der Mondsknoten in 20 Julianischen Jahren 386° 50′ 15″ beträgt, wie man aus den in der Theorie des Mondes benutzten Beobachtungen findet; so wird die mittlere Bewegung derselben in einem siderischen Jahre = 19° 20′ 32″,0 und wir haben
Hieraus erhält man die stündliche Bewegung der Knoten in den Quadraturen = 16″,3 und ihre grösste Gleichung in den Octanten = 1° 29′ 57″.[30]
§. 38. Aufgabe. Man soll die stündliche Aenderung der Neigung der Mondbahn gegen die Ebene der Ekliptik bestimmen.
Es seien A und a die Syzygien, Q und q die Quadraturen, N und n die Knoten, P der Ort des Mondes in seiner Bahn, p die Projection dieses Ortes auf die Ebene der Ekliptik und mTl die augenblickliche Bewegung der Knoten, wie oben. Man fälle auf die Linie Tm die Perpendikel PG, pG und verlängere dieses, bis es Tl in g schneidet und ziehe auch Pg. Der Winkel PGp wird die Neigung der Mondbahn gegen die Ebene der Ekliptik sein, wenn der Mond sich in P befindet, der Winkel Pgp dieselbe Neigung in dem nächstfolgenden Augenblick und daher der Winkel GPg die augenblickliche Aenderung der Neigung. Nun steht dieser Winkel GPg zum Winkel GTg in einem Verhältniss, welches aus den beiden einzelnen Verhältnissen GT : PG und Pp : PG zusammengesetzt ist.[31] Setzt man daher das Moment der Zeit gleich einer Stunde, also (nach §. 34.)
so wird GPg, d. h. die stündliche Aenderung der Neigung, sich zu 33″,2 verhalten, wie
Das oben Gesagte findet unter der Voraussetzung statt, dass der Mond sich gleichförmig in einer Kreisbahn bewege. Ist aber diese Bahn elliptisch, so wird die Bewegung der Knoten kleiner, im Verhältniss der kleinen Axe zur grossen, wie wir oben gezeigt haben. In demselben Verhältniss wird dann auch die Veränderung der Neigung kleiner werden.
Zusatz 1. Man errichte TF perpendikulär auf Nn und nehme pM als stündliche Bewegung des Mondes in der Ebene der Ekliptik an, hierauf fälle man auf QT die Perpendikel pK und Mk und verlängere sie, bis sie TF in H und h schneiden.
Alsdann haben wir
und
Hiernach und nach Gl. 2. wird die stündliche Veränderung der Neigung sich zu 33″,2 verhalten, wie
Zusatz 2. Wenn daher die Erde und der Knoten am Ende jeder Stunde aus ihren neuen Orten entfernt und immer augenblicklich an ihre früheren Orte zurückgebracht werden, dergestalt, dass ihre gegebene Lage während eines ganzen periodischen Monats unverändert bleibt; so wird die ganze Aenderung der Neigung während dieser Zeit sich zu 33″,2 verhalten, wie das Produkt aus der Summe aller Flächen HpMh, welche während des Umlaufes des Punktes p beschrieben worden, in die Grösse AZ · TZ · zu Mp · AT³, d. h. wie
oder was auf dasselbe hinauskommt, wie
Zusatz 3. Bei einer gegebenen Lage der Knoten wird daher die mittlere stündliche Veränderung, welche, während eines Monats fortgesetzt, jene ganze monatliche Veränderung hervorbringen würde, sich zu 33″,2 verhalten, wie AZ · TZ · : 2 · AT²
d. h. (weil Pp : PG = sin PGp : Radius und
wie das Produkt aus dem Sinus der Neigung in den Sinus des doppelten Winkelabstandes der Knoten von der Sonne zum vierfachen Quadrat des Radius.[32]
Zusatz 4. Die stündliche Veränderung der Neigung verhält sich, wenn die Knoten in den Quadraturen liegen, (nach diesem Paragraphen) zu 33″,2, wie JT · AZ · TG · : AT³, d. h. wie
oder wie der Sinus des doppelten Winkelstandes des Mondes von den Quadraturen, multiplicirt im , zum doppelten Radius. Die Summe aller stündlichen Bewegungen während der Zeit, wo der Mond bei dieser Lage der Knoten von der Quadratur zur Syzygie fortgeht (d. h. in der Zeit von 1771/6 Standen), wird sich also zur Summe eben so vieler Winkel von 33″,2, oder zu 5878″ verhalten, wie die Summe aller Sinusse des doppelten Winkelabstandes des Mondes von den Quadraturen, multiplicirt in , zur Summe eben so vieler Durchmesser, d. h. wie der Durchmesser, multiplicirt in zur Peripherie[34]. Dieses Verhältniss wird nun, wenn man die Neigung = 5° 1′ setzt, gleich dem 7 · : 22 = 278 : 10000.
Die ganze, aus der Summe aller stündlichen Bewegungen, welche während der eben besprochenen Zeit stattfinden, zusammengesetzte Veränderung ist also = 163″ = 2′ 43″.
§. 39. Aufgabe. Man soll für eine gegebene Zeit die wahre Neigung der Mondbahn gegen die Ebene der Ekliptik finden.
Ist AD der Sinus der grössten und AB der Sinus der kleinsten Neigung, so halbire man BD in C und schlage aus C mit BC einen Kreis BGD. Hierauf nehme man auf AC die Linie CE so an, dass
sei, mache den Winkel AEG gleich dem doppelten Winkelabstande der Knoten von den Quadraturen zu der gegebenen Zeit. Fällt man hierauf das Perpendikel GH auf AD, so wird AH der Sinus der gesuchten Neigung sein.
Es ist nämlich GE² = GH² + HE², = BH · HD + HE², = BH · BD + HE² – BH², = BH · BD + BE² – 2BH · BE, = BE² + 2EC · BH, = 2CE · AB + 2EC · BH (Gl. 1), endlich
Da nun 2CE gegeben ist, so wird GE² proportional AH. Stellt jetzt der Winkel AEg den doppelten Winkelabstand der Knoten von den Quadraturen, am Ende eines beliebigen gegebenen Momentes der Zeit dar; so wird der Bogen Gg, weil der Winkel GEg gegeben ist, dem Abstande GE proportional.
Ferner ist aber
folglich wird Hh proportional GH · Gg oder GH · GE, d. h. · GE² oder · AH.
Hh steht also im zusammengesetzten Verhältniss von AH und dem Sinus des Winkels AEG. Wenn daher die Linie AH in irgend einem Falle dem Sinus der Neigung gleich ist, so wird sie um denselben Zuwachs wie dieser Sinus, nach §. 38., Zusatz 3., grösser und kleiner werden und ihm immer gleich bleiben.[35] Die Linie AH ist aber diesem Sinus gleich, wenn der Punkt G in B und D fällt; folglich wird sie ihm immer gleich bleiben. W. z. b. w.
Ich habe bei diesem Beweise vorausgesetzt, dass der Winkel BEG, welcher dem doppelten Abstande der Knoten von den Quadraturen gleich ist, gleichförmig wachse, weil es bei dieser Gelegenheit überflüssig sein würde, auf alle kleinen Ungleichheiten Rücksicht zu nehmen. Setzen wir nun voraus, dass der Winkel BEG = 90°, und dass in diesem Falle Gg die stündliche Zunahme des doppelten Abstandes der Knoten von der Sonne sei. Alsdann wird (nach §. 38., Zusatz 3.) die stündliche Aenderung der Neigung sich zu 33″,2 verhalten, wie das Produkt aus dem Sinus der Neigung AH und dem Sinus des rechten Winkels BEG, welcher dem doppelten Abstande der Knoten von der Sonne gleich ist, zum vierfachen Quadrat des Radius. Dieses Verhältniss wird nun (weil die mittlere Neigung ungefähr = 5° 8′,5 ist)
Die ganze, dem Unterschiede BD der Sinusse entsprechende, Veränderung verhält sich aber zu dieser stündlichen Veränderung, wie der Durchmesser BD zum Bogen Gg, d. h. sie steht im zusammengesetzten Verhältniss des Durchmessers BD zur halben Peripherie BGD und der Zeit von 2079,7 Stunden, welche der Knoten braucht, um von den Quadraturen zu den Syzygien fortzugehen, zu 1 Stunde. Verbindet man diese Verhältnisse, so wird die ganze Veränderung BD : 33″,2 = 224 · 7 · 2079,7 : 110000 = 29646 : 1000 und
Dies ist die grösste Veränderung der Neigung, so lange man auf den Ort des Mondes in seiner Bahn keine Rücksicht nimmt. Befinden sich nämlich die Knoten in den Syzygien, so ändert sich diese Neigung nicht durch die verschiedene Lage des Mondes; sind aber die Knoten in den Quadraturen, so ist die Neigung um 2′ 43″ kleiner, wenn der Mond sich in den Syzygien, als wenn er sich in den Quadraturen befindet. Dies haben wir im §. 38., Zusatz 4., gezeigt. Nimmt man die Hälfte dieses Unterschiedes von 1′ 21″,5 von obiger Grösse fort, so wird die ganze mittlere Veränderung BD in den Quadraturen des Mondes = 15′ 2″; addirt man jene Hälfte, so wird die ganze Veränderung in den Syzygien des Mondes = 17′ 45″.
Befindet sich daher der Mond in den Syzygien, so wird die ganze Veränderung beim Uebergange der Knoten von den Quadraturen zu den Syzygien = 17′ 45″.
Ist also die Neigung, im Fall die Knoten sich in den Syzygien befinden, = 5° 17′ 20″, so wird sie, wenn die Knoten sich in den Quadraturen und der Mond sich in den Syzygien befindet, = 4° 59′ 35″.
Dies wird durch die Beobachtungen bestätigt.
Will man hierauf die Neigung dar Bahn für den Fall kennen lernen, dass der Mond sich in den Syzygien und die Knoten sich in einem beliebigen Orte befinden, so setze man
mache den Winkel AEG gleich dem doppelten Winkelabstande der Knoten von den Quadraturen, und es wird alsdann AH dem Sinus der gesuchten Neigung gleich sein. Die Neigung dieser Bahn ist für den Fall, dass der Mond um 90° von den Knoten entfernt ist, der eben bestimmten gleich.
In anderen Orten des Mondes gleicht sich die Ungleichheit jedes Monats, welche in der Veränderung der Neigung stattfindet, bei der Berechnung der Breite des Mondes aus und wird gewissermassen durch die monatliche Ungleichheit der Bewegung der Knoten compensirt. Dies haben wir bereits oben bemerkt, und man kann daher jene bei der Berechnung der Breite vernachlässigen.
§. 40. Anmerkung. Ich habe durch diese Berechnung der Bewegungen des Mondes zeigen wollen, dass man sie mittelst der Theorie der Schwere aus ihren Ursachen ableiten könne. Nach derselben Theorie habe ich noch gefunden, dass die jährliche Gleichung in der mittleren Bewegung des Mondes aus der verschiedenen Ausdehnung seiner Bahn durch die Kraft der Sonne, nach §. 107., Zusatz 6. des ersten Buches, entspringt.
Diese Kraft ist nämlich grösser im Perigeum der Sonne und dehnt daher die Mondbahn aus; im Apogeum ist sie hingegen kleiner und gestattet, dass jene Bahn sich zusammenziehe. Nun bewegt sich der Mond langsamer in der ausgedehnten, und geschwinder in der zusammengezogenen Bahn. Die jährliche Gleichung, durch welche man diese Ungleichheit compensirt, ist Null im Apogeum und im Perigeum der Sonne, sie steigt im mittleren Abstande der Sonne von der Erde bis auf ungefähr 11′ 50″ und ist an anderen Orten der Mittelpunktsgleichung der Sonne proportional. Sie wird zur mittleren Bewegung des Mondes addirt, wenn die Erde von ihrem Aphel zum Perihel übergeht; im entgegengesetzten Theile der Bahn wird sie von ihr subtrahirt.
Setzt man den Radius der grossen Bahn = 1000, und die Excentricität der Erde = 167/8, so wird diese Gleichung, wenn sie ihren grössten Werth hat, nach der Theorie der Schwere = 11′ 49″.
Die Excentricität der Erde scheint aber etwas grösser zu sein, und vergrössert man sie, so muss diese Gleichung in demselben Verhältniss annehmen. Setzt man daher die Excentricität = 1611/12, so wird die grösste Gleichung = 11′ 51″.
Ich habe auch gefunden, dass im Perihel der Erde das Apogeum und die Knoten des Mondes, wegen der grösseren Kraft der Sonne, geschwinder als im Aphel fortgingen, und zwar im umgekehrten dreifachen Verhältniss des Abstandes der Erde von der Sonne. Hieraus schliesst man, dass die jährlichen Gleichungen dieser Bewegungen der Mittelpunktsgleichung der Sonne proportional sind. Nun steht die Bewegung der Sonne im umgekehrten doppelten Verhältniss des Abstandes der Erde von ihr, und es beträgt die grösste Mittelpunktsgleichung, welche durch diese Ungleichheit hervorgebracht wird, 1° 56′ 20″, was mit der oben erwähnten Excentricität von 0,01611/12 = 0,016917 übereinstimmt.
Stände die Bewegung der Sonne im umgekehrten dreifachen Verhältniss des Abstandes, so würde diese Ungleichheit 2° 54′ 30″[36] als grösste Gleichung hervorbringen. Die grössten Gleichungen, welche durch die ungleichen Bewegungen des Apogeums und der Knoten des Mondes hervorgebracht werden, verhalten sich also zu 2° 54′ 30″, wie die mittlere tägliche Bewegung der zwei letzteren, zur mittleren täglichen Bewegung der Sonne.
Hieraus folgt, dass die grösste Gleichung der mittleren Bewegung des Apogeums 19′ 43″, die grösste Gleichung der mittleren Bewegung der Knoten 9′ 24″ beträgt.[37] Die erstere ist additiv und die letztere subtractiv, wenn die Erde vom Perihel zum Aphel fortschreitet; das Gegentheil findet statt, wenn sie sich im entgegengesetzten Theile der Bahn befindet.
Durch die Theorie der Schwere ist es gewiss, dass die Wirkung der Sonne auf den Mond ein wenig stärker ist, wenn die grosse Axe der Mondbahn durch die Sonne geht, als wenn dieselbe auf die, die Sonne und Erde verbindende gerade Linie senkrecht ist; folglich wird die Mondbahn im ersten Falle etwas weiter sein, als im letzteren.[38] Hieraus erhält man eine andere Gleichung der mittleren Bewegung des Mondes, welche von der Lage des Mond-Apogeums in Bezug auf die Sonne abhängt, und dieselbe hat ihren grössten Werth, wenn jenes Apogeum sich mit der Sonne im Octanten befindet; sie verschwindet hingegen, wenn dasselbe zu den Syzygien oder den Quadraturen gelangt. Sie wird zur mittleren Bewegung addirt, wenn das Mond-Apogeum von der Quadratur der Sonne zur Syzygie übergeht, im entgegengesetzten Falle wird sie subtrahirt. Diese Gleichung, welche ich die halbjährige nennen werde, steigt in den Octanten, wo sie am grössten ist, auf ungefähr 3′ 45″, so weit ich aus den Beobachtungen habe schliessen können. Dies ist ihr Werth in der mittleren Entfernung der Sonne von der Erde, sie muss aber im umgekehrten dreifachen Verhältniss jener Entfernung vermehrt oder vermindert werden, und beträgt daher in der grössten Entfernung der Sonne sehr nahe 3′ 34″, hingegen in der kleinsten Entfernung 3′ 56″[39]. Liegt das Apogeum des Mondes ausserhalb der Octanten, so wird diese Gleichung kleiner und verhält sich zur grössten, wie der Sinus des doppelten Winkel-Abstandes des Mond-Apogeums von der nächsten Syzygie oder Quadratur zum Radius.
Nach derselben Theorie der Schwere ist die Wirkung der Sonne auf den Mond ein wenig grösser, wenn die durch die Mondknoten gezogene Linie durch die Sonne geht, als wenn sie die, Sonne und Erde verbindende, Linie rechtwinkelig durchschneidet. Hieraus ergiebt sich eine andere Gleichung der mittleren Bewegung des Mondes, welche ich die zweite halbjährige nennen werde, und die am grössten ist, wenn die Knoten sich in den Octanten mit der Sonne befinden und verschwindet, wenn sie in den Quadraturen oder den Syzygien liegen. Für andere liegen der Knoten ist sie dem Sinus des doppelten Winkelabstandes des einen oder anderen Knoten von der nächsten Syzygie oder Quadratur proportional. Sie wird zur mittleren Bewegung des Mondes addirt, wenn die Sonne rückläufig von dem ihr nächsten Knoten, hingegen subtrahirt, wenn diese rechtläufig absteht. In den Octanten, wo sie am grössten ist, steigt sie für die mittlere Entfernung der Sonne von der Erde bis auf 47″, wie ich durch die Theorie der Schwere gefunden habe. Für andere Entfernungen der Sonne von der Erde ist diese, in den Octanten der Knoten grösste Gleichung dem Cubus der Entfernung umgekehrt proportional und steigt daher im Perigeum der Sonne auf 49″, wogegen sie im Apogeum nahe auf 45″ sinkt.[40]
Nach der Theorie der Schwere geht das Apogeum des Mondes am stärksten vorwärts, wenn es mit der Sonne in Opposition oder Conjunction, und am stärksten rückwärts, wenn es mit ihr in Quadratur steht (§. 107., Zusatz 9., des ersten Buches). Im ersten Falle wird die Excentricität am grössten, im letzteren am kleinsten. Nach §. 107, Zusätze 7., 8. und 9. des ersten Buches, sind diese Ungleichheiten sehr gross und bringen die Hauptgleichung des Apogeums hervor, welche ich die halbjährige nennen werde. Die grösste halbjährige Gleichung beträgt ungefähr 12° 18′, so weit ich aus den Beobachtungen habe schliessen können. Horrox, unser Landsmann, war der erste, welcher den Satz aufstellte, dass der Mond sich in einer Ellipse um die Erde bewege, in deren unterem Brennpunkte sich die letztere befinde. Halley setzte den Mittelpunkt dieser Ellipse auf einen Epicykel, dessen Mittelpunkt sich gleichförmig um die Erde drehe. Aus dieser Bewegung auf dem Epicykel entspringen die Ungleichheiten beim Vor- und Rückwärtsschreiten des Apogeums, wovon wir gesprochen haben, so wie die Grösse der Excentricität.
Setzen wir voraus, dass die mittlere Entfernung des Mondes von der Erde = 100000, T die Erde und TC die mittlere Excentricität des Mondes = 5505 sei. Es werde TC so bis B verlängert, dass BC der Sinus der grössten halbjährigen Gleichung von 12° 18′ für den Radius TC sei; alsdann wird der aus C mit dem Radius CB beschriebene Kreis BDA dieser Epicykel sein, auf welchem der Mittelpunkt der Mondbahn sich befindet und seinen Umlauf in der Reihenfolge der Buchstaben B, D, A macht. Man nehme hierauf den Winkel BCD gleich dem doppelten jährlichen Argument, oder gleich dem doppelten Winkelabstande des wahren Sonnenortes vom einmal verbesserten Apogeum des Mondes; alsdann wird CTD die halbjährige Gleichung des Mond-Apogeums, und TD die Excentricität seiner Bahn, welche gegen das zum zweiten Mal verbesserte Apogeum gerichtet ist, darstellen. Hat man aber die Excentricität, die mittlere Bewegung und das Apogeum des Mondes, wie auch die grosse Axe seiner Bahn = 200000, so erhält man daraus, nach den gewöhnlichen Methoden, den wahren Ort des Mondes in seiner Bahn und seinen Abstand von der Erde.
Der Mittelpunkt der Mondbahn bewegt sich schneller um den Mittelpunkt C im Perihel der Erde, als in ihrem Aphel, wegen der grösseren Kraft der Sonne, und zwar im umgekehrten dreifachen Verhältniss des Abstandes der Erde von der Sonne. Wegen der, im jährlichen Argument mit einbegriffenen Mittelpunktsgleichung der Sonne, bewegt sich der Mittelpunkt der Mondbahn schneller auf dem Epicykel und zwar im umgekehrten doppelten Verhältniss des Abstandes der Erde von der Sonne. Damit derselbe sich noch geschwinder, im umgekehrten einfachen Verhältniss des Abstandes bewege, ziehe man aus dem Mittelpunkte D der Bahn die gerade Linie DE nach dem Apogeum des Mondes oder ∥ TC und nehme den Winkel EDF gleich dem Ueberschusse des besprochenen jährlichen Arguments über den Winkelabstand des Mond-Apogeums vom Perigeum der Sonne, rechtläufig gezählt, oder was dasselbe ist, es sei der Winkel CDF gleich der Ergänzung der wahren Anomalie der Sonne zu 360°.[41] Hierauf nehme man DF : DC im zusammengesetzten Verhältniss der doppelten Excentricität der grossen Bahn zum mittleren Abstande der Sonne von der Erde, und der mittleren täglichen Bewegung von ihrem eigenen Apogeum ab, d. h. DF : DC = [42], oder einfach DF : DC = 3 : 100.
Gesetzt, der Mittelpunkt der Mondbahn befinde sich im Punkte F und auf einem Epicykel, dessen Mittelpunkt D und dessen Radius DF sei; er vollende ferner seinen Umlauf, während der Punkt D auf der Peripherie DABD vorwärts geht. Auf diese Weise wird die Geschwindigkeit, mit welcher der Mittelpunkt der Mondbahn die um den Mittelpunkt C beschriebene Curve beschreibt, sehr nahe im umgekehrten Verhältniss des Cubus des Abstandes der Sonne von der Erde stehen, wie dies der Fall sein muss.
Die Berechnung dieser Bewegung ist schwierig, man kann sie aber durch folgende Annäherung erleichtern. Man nehme den mittleren Abstand des Mondes von der Erde = 100000 und die Excentricität TC = 5505, wie oben an; die Linie CB oder DC wird 1172,73 und DF = 35,3 sein[43]. Diese Linie unterspannt im Abstande TC an der Erde denjenigen Winkel, welchen die Verlegung des Mittelpunktes der Bahn von D nach F in der Bewegung dieses Mittelpunktes hervorbringt. Verdoppelt man aber diese Linie in einer, der die Erde und den unteren Brennpunkt der Mondbahn verbindenden Linie, parallelen Richtung, so unterspannt sie denselben Winkel, und daher ist dieser demjenigen gleich, welchen diese Versetzung in der Bewegung des Brennpunktes hervorbringt. Im Abstande des Mondes von der Erde unterspannt sie ferner den Winkel, welchen eben diese Versetzung in der Bewegung des Mondes hervorbringt, so dass dieser Winkel die zweite Gleichung des Mittelpunktes genannt werden kann. Dieselbe ist im mittleren Abstande des Mondes von der Erde sehr nahe dem Sinus des Winkels proportional, welchen jene Linie DF mit der von F nach dem Monde gezogenen Linie bildet, und sie steigt, wenn sie am grössten ist, bis auf 2′ 25″.[44] Den Winkel aber, welchen DF mit der, aus F nach dem Monde gezogenen Linie bildet, findet man, indem man den Winkel EDF von der mittleren Anomalie des Mondes subtrahirt, oder indem man den Winkelabstand des Mondes von der Sonne zum gegenseitigen Winkelabstande der Apogeen des Mondes und der Sonne addirt. Setzt man diesen Winkel = a, so ist die vierte Proportionale x in der Proportion Radius : sin a = 2′ 25″ : x der zweiten Mittelpunktsgleichung gleich, welche man addiren muss, wenn jener Winkel < 180° ist, hingegen subtrahiren, wenn er > 180° ist. Auf diese Weise wird man seine Länge in den Syzygien der Lichtgrenzen (luminarium) erhalten.
Da die Atmosphäre der Erde das Sonnenlicht bis zu einer Höhe von 35 bis 40 Meilen bricht, und es bei dieser Brechung um den Schatten der Erde verbreitet; da also das so an den Grenzen des Schattens verbreitete Licht diese Grenzen ausdehnt und erweitert: so addire ich 1 oder 1⅓ Secunden zum Durchmesser des Schattens, welchen die Parallaxe des Mondes bei den Verfinsterungen des letzteren hervorbringt.[45]
Uebrigens muss die Theorie des Mondes durch die Erscheinungen geprüft und so bestätigt werden, und zwar zuerst in den Syzygien, hierauf in den Quadraturen und endlich in den Octanten. In dieser Absicht habe ich mit ziemlicher Genauigkeit die mittleren Bewegungen des Mondes und der Sonne im Meridian der Königlichen Sternwarte zu Greenwich beobachtet. Für den 31. Dec. 1700 alt. Styls fand ich den mittleren Ort der Sonne in 290° 43′ 20″, ihr Apogeum in 97° 44′ 30″, den mittleren Ort des Mondes in 315° 21′ 0″, sein Apogeum in 338° 20′ 0″ und seinen aufsteigenden Knoten in 147° 24′ 20″ Länge. Der Meridian-Unterschied zwischen der Greenwicher und Pariser Sternwarte beträgt 9m 20s (neu 20s,9); die mittlere Bewegung des Mondes von seinem Apogeum kennt man noch nicht hinreichend genau.
Bemerkungen und Erläuterungen [des Übersetzers]
[Bearbeiten]- ↑ [629] No. 237. S. 416. Nach den Werthen von Hansen a. a. O. wird dieses Verhältniss (27,321661)² : (365,25637)² = 1000 : 178312 = 1 : 17812/40.
- ↑ [629] No. 238. S. 417. Bringt man hier den in der vorstehenden Bemerkung aufgeführten Werth 178,312 in Anwendung, so erhält man das Verhältniss 1: 636619,3.
- ↑ [629] No. 239. S. 418. (Fig. 191.) Es ist Δ Ppq ∼ PKT, und weil pq = Kk, so wird Kk = . Ferner FK · Kk = · Pp, d. h. weil Pp constant ist, FK · Kk proportional .
- ↑ [629] No. 240. S. 418. EL ist proportional PK · TK = PT sin PC · PT cos PC, und wird daher ein Maximum für PC = 45°. Ferner wird in diesem Falle FK · Kk = ½ · Pp = ½TP · Pp.
- ↑ [629] No. 241. S. 419. Die Geschwindigkeit des Mondes ist dem Increment (Moment) der Fläche proportional, also im Mittel = 11915 · a, wo a irgend eine Constante bezeichnet. Mithin wird die Geschwindigkeit im Texte, welche 100/11915 von der des Mondes gleich ist, nun 100 · a und so die in den Syzygien und den Quadraturen stattfindende Geschwindigkeit respective 11965 · a und 11865 · a.
- ↑ [629] No. 242. S. 419. Es ist nämlich FKCG : GCF = (GC + FK)CK : GC · CT = CT² – KT² : CT² = PK² : PT² = PT · Pd : PT² = Pd : PT.
- ↑ [629] No. 243. S. 419. Nach dem Vorhergehenden ist nämlich das Moment dieser Fläche proportional
[630]
109,73 + Pd, für den Radius PT = 100, oder 109,73 + Pd „ „ „ = 1 „ 219,46 + 2Pd „ „ „ = 1. Nun ist Pd = sinus versus PC und 2 Pd = Pd' = sinus versus PCP' = sinus versus 2 · PC.
- ↑ [630] No. 244. S. 420. Setzt man die stündliche Bewegung = dv, den Abstand = r und die beschriebene Fläche = f; so wird f = ½r²dv und r = .
- ↑ [630] No. 245. S. 420. Setzt man die Geschwindigkeit a'c' = v, den Radius des osculirenden Kreises a'd = r und die Anziehung b'c' = k; so ist offenbar sehr nahe 2kr = v² und , und offenbar der Krümmung proportional. Für ab = a'b' oder ac = a'c' und beide unendlich klein, kann man bc = sin bac oder = tang bac und b'c' = sin b'a'c' oder = tang b'a'c' setzen.
- ↑ [630] No. 246. S. 420. In der Entfernung N ist die Schwere des Mondes gegen die Erde = 178725, mithin in der Entfernung AT = . Die Kraft der Sonne wirkt in den Syzygien derjenigen der Erde entgegen und ist im Abstande N von der Erde = 2000; daher im Abstande AT = . Mithin wird die ganze erziehende Kraft proportional oder auch, indem man durch N² dividirt, proportional . Weil aber sehr nahe AT = CT, wird und ; mithin obige Kraft sehr nahe proportional ; oder 178725CT² · N – 2000AT² · CT. Aehnlich für die Quadraturen.
- ↑ [630] No. 247. S. 422. (Fig. 193.) Wir wollen der Kürze wegen
die Krümmung der Ellipse in A und C durch EA, EC „ „ „ Figur Tpa „ a „ C „ Ba BC „ „ des ersten Kreises „ KA „ „ „ zweiten „ „ KC bezeichnen. Denkt man sich nun aus T mit TA einen Kreisbogen geschlagen, welcher durch A und a gehen wird und hierauf von A und a aus auf der Ellipse und Bahn gleichzeitig beschriebene kleine Stücke v und v' abgetragen, so dass in beiden Fällen der Körper durch die anziehende Kraft der Erde ihr um gleiche Stücke e näher gebracht sein [631] würde; so ist dem Unterschiede der Krümmungen der Bahn in a und des Kreises in a, oder Ba – Ka proportional (Bem. 245.) Ferner ist dem Unterschiede der Krümmung der Ellipse in A und desselben Kreises, oder EA – KA proportional. Wir haben daher
1. Ba – KA : EA – KA = = v² : v'² = CTP² : CTp².Auf ähnliche Weise ergiebt sich das letzte Verhältniss im Texte
1a. EC – KC : BC – KC = CTp² : CTP².Ferner ist KA proportional , KC proportional , EA ist dem Radius des osculirenden Kreises in A und EC den Radius des osculirenden Kreises in C umgekehrt proportional. Der erste Radius ist aber = , der letztere = , also
2. EA : KA = = TA² : TC².3. KA : KC = = TC : TA.4. KC : EC = = TA² : TC². - ↑ [631] No. 248. S. 422. Aus Proportion 2. folgt nämlich
5. EA – KA : KA = TA² – TC², aus 1. und 5.6. Ba – KA : KA = (TA² – TC²)CTP² : TC² · CTp².
hieraus
7. Ba : KA – TA² · CTP² + TC²(CTp² – CTP²) : TC² · CTp².Ferner aus Proportion 4.
8. KC : EC – KC = TA² : TC² – TA²,hieraus und aus 1a.
9. KC : BC – KC = TA² · CTp² : (TC² – TA²)CTP²oder
10. KC : BC = TA² · CTp² : TC² · CTP² + TA²(CTp² – CTP²),hieraus und aus 3.
11. KA : BC = TA² · TC · CTp² : TA · TC² · CTP² + TA²(CTp² – CTP²).Durch die Verbindung der Proportionen 7. und 11. erhalten wir endlich
12. Ba : BC = TA4 · TC · CTp² · CTP² + TA² · TC³ · CTp²(CTp² – CTP²) : TA · TC4, CTp² · CTP² + TA³ · TC², CTp²(CTp² – CTP²)Ba : BC = TA³ + TA · TC² : TC³ + TA² · TC .Man hätte übrigens auch die Verhältnisse EA : Ba und EC : BC unmittelbar [632] nach §. 84, Zusatz 3 des ersten Buches auf folgende Weise finden können. Setzte man statt des dortigen
A hier TA T „ TC R „ F „ CTP G „ CTp; so würde das Verhältniss der Kräfte für E und B in den Punkten A und a und das Verhältniss der Geschwindigkeiten CTP : CTp; mithin EA : Ba = oder auch
13. EA : Ba = TA² · : TA² + TC² · .Vertauscht man hier
TA mit TC, A „ C und umgekehrt, so erhält man unmittelbar
14. EC : BC = TC² · : TC² + TA² · .Aus diesen beiden Gleichungen 13 und 14 würde man leicht, durch Benutzung der Proportionen 2, 3 und 4, die Proportion 12 wieder herleiten können.
- ↑ [632] No. 249. S. 423. Dem Winkel CTP in der Ellipse entspricht die mittlere Bewegung CTP' im Kreise, und es ist daher tang CTP : tang CTP' = PQ : P'Q = AT : TC = 69 : 70.
- ↑ [632] No. 250. S. 423. Bestimmt man einen Winkel CTP'' so, dass tang CTP'' = tang CTP so wird, weil tang CTP = tang CTP', tang CTP'' = tang CTP'.
- ↑ [632] No. 251. S. 429. (Fig. 196.) Aus fg = in 5. folgt nach 4. , d. h. T, G und g liegen in gerader Linie und es ist fTg = FTG. Allgemein ist aber sin fTg = sin FTG = sin fgT : sin FGT näherungsweise = , weil genähert fgT = FGT. Es ist aber wirklich (nach 6.) fg = , d. h. das fg in 5. [633] muss durch multiplicirt werden. Demnach wird statt
jetztund = sin fTg : sin FTG = fp · cY : fY · cp.
- ↑ [633] No. 252. S. 430. Man setze die Radienvectoren in den Quadraturen, Octanten und Syzygien respective gleich q, o, s, die Winkelgeschwindigkeit allgemein = dv, die jenen entsprechenden Zeitelemente gleich t(q), t(o), t(s); alsdann haben wir nach dem Frühern (§. 30.) q²dv : s²dv = 10973 : 11073; also weil o²dv = ½(q² + s²)dv, o²dv : = 11023 : 50. Jene Verhältnisse der Flächenelemente würden für gleiche Zeitelemente gelten, wogegen bei verschiedenen Zeitelementen diese den ersteren umgekehrt proportional sind; demnach t(o) : = 11023 : 50.
- ↑ [633] No. 253. S. 431. In derselben Zeit, wo der Mond in seiner Bahn den Weg PM zurücklegt, beschreibt er, vermöge der während dieser kurzen Zeit als constant zu betrachtenden Sonnenkraft 3 · JT den Weg SM und dieser ist alsdann 3 · JT · Q², wenn t jene kleine Zeit bezeichnet.
- ↑ [633] No. 254. S. 431. Es verhält sich die übrigbleibende Bewegung zur ganzen Bewegung, wie 11023² : 11073², d. h. wie (11073 – 50)² : 11073² und wenn man 50² gegen 11073² vernachlässigt, beiläufig
11073² – 100 · 11073 : 11073², 11073 – 100 : 11073, 10973 : 11073,
woraus die Verhältnisse 100 : 10973 und 100 : 11073 im Text unmittelbar hervorgehen.
- ↑ [633] No. 255. S. 431. Man setze den Winkel, welchen der Mond im Octanten O in einer gegebenen Zeit zurücklegt = L, den derselben Zeit im Punkte P entsprechenden Winkel = L + x, endlich den der Syzygie A entsprechenden L + l. Ferner sei die, derselben Zeit entsprechende Bewegung des Knotens in O = N – d und in P = N. Da nun die letzteren Bewegungen dem Quadrat der Zeiten proportional sind, so wird N – d : N = L² : (L + x)² = L² : L² + 2Lx + x² oder, weil x in Vergleichung mit L sehr klein ist, genähert
1. N – d : N = L : L + 2x
und hieraus N : d = L + 2x : 2x oder wieder genähert
2. N : d = L : 2x.Bezeichnet nun A die Bewegung des Knotens in der Syzygie A, und a deren Increment, so ist nach 2.
3. a : A = 2l : Lund nach 2. und 3. aN : d · A = l : x oder auch
4. d : a = xN : l · A.[634] Nach der Stelle im Texte (§. 30) ist x : l = TE² – ½AT² : ½AT² und so xN : lA = N(TE² – ½AT²) : ½A · AT², also nach 4.5. d : a = N(TE² – ½AT²) : ½A · AT².Nun ist TE = AT · sin PTQ = AT · cos AP, also TE² – ½AT² = AT² cos AP² – ½AT² = ½AT² cos 2 · AP), und nach 5.
6. d : a = N · AT · cos 2AP : A · AT. - ↑ [634] No. 256. S. 431. Es sei die Syzygia in A, die Quadranten in Q und der Octant in O. Ferner sei AP = OP' = OP'' = QP''' = AK, PE auf AT, PF' auf KT perpendiculär, AL = AP' und P'G auf LT perpendiculär. Je nachdem der Mond sich in A, P, P', P'', P''' befindet, mögen die stündlichen Bewegungen der Knoten Q und q durch jene Buchstaben selbst, die Decremente dieser Bewegungen in A, P, P' durch a, p, p', die Incremente in P'' und P''' durch p'', p''' bezeichnet werden.
Nach der vorhergehenden Bemerkung (255) ist nun
1. p : a = P · TF : A · TA,ferner weil PQJ = 2 · PQ, nach §. 30 P : A = JF : 2AT und so,
2. p : a = JF · TF : 2 · AT²,ebenso
3. p''' : a = KF · TF : 2 · AT²,indem KF = TA sin vers. PK = TA sin vers. 2 · AP = TA sin vers. 2 · P'''Q und TF = TA cos 2 · AP = TA cos 2 · P'''Q. Aus 2. und 3. folgt p – p''' : a = (JF – KF)TF : 2AT² = 2TF² : 2 · AT² oder
4. p – p''' : a = TF² : AT²,ähnlich
5. p' – p'' : a = TG² : AT²und aus 4. und 5.
6. p + p' – p'' – p''' : = TF² + JG² : AT².Da nun TF = TA · cos 2 · AP, TG = TA cos 2 · AP' = TA cos 2 (AO – OP') = TA cos 2(45° – AP) = TA sin 2 · AP, also TF² + TG² = TA², so wird aus 6. p + p' – p'' – p''' = a.
- ↑ [634] No. 257. S. 432. Es ist nämlich Aa : ZY = AT : AZ, wo Aa und AT gegebene Grössen sind.
- ↑ [634] No. 258. S. 433. Setzt man die mittlere Bewegung des Knotens im Orte N = m(n), in der Quadratur, wo sie am grössten und = 39°,6355 ist, = m(g), endlich die Bewegung der Sonne = 360° = m(s); so ist m(s) : m(g) = 360 : 39,6355, m(g) : m(n) = AT² : AZ², mithin m(s) : m(n) = 360 · AT² : 39,6355AZ² = 9,0827666AT² : AZ² = α · AT² : AZ², wo der Kürze wegen 9,0827666 = α gesetzt ist. Ferner wird m(s) : n(s) + m(n) = α · AT² : α · AT² + AZ² und daher, wenn t(s), t(n) die, den Bewegungen [635] m(s), m(n) respective entsprechenden Zeiten bezeichnen, weil m(n) der m(s) entgegengesetzt ist und daher t(s) durch t(n) verkürzt wird, t(s) : t(s) – t(n) = α · AT² + AZ² : α · AT².
- ↑ [635] No. 259. S. 433. Es ist
1. dZ · ZY : ATa = AZ² : α · AT² + AZ² = t(n) : t(s),
da aber ATa = ½Aa · AT und Aa : YZ = AT : AZ, also Aa = ; so wird dZ · ZY : ATa = dZ · ZY : ½ = dZ · BZ : ½AT² und es geht die Proportion 1. über in
2. dZ : ½AZ = AT² : α, AT² + AZ².dZ · ZY entspricht t(n), d. h. den durch die Knotenbewegung hervorgebrachte Decrement der Zeit, während der durch ATa dargestellten Zeit; NdZ stellt das, dem Sector ATN entsprechende Decrement dar und da NATN die ganze unverkürzte Zeit darstellte, so wird NATN – NdZ die ganze, vermöge der Knotenbewegung verkürzte Zeit darstellen.
- ↑ [635] No. 260. S. 434. Wir haben im Text aZ : AZ = AZ² : α · AT² + AZ² = t(n) t(s), also auch aZ · ZY : AZ · ZY = t(n) : t(s) oder aZN : AZN = T(n) : T(s), wo T(n) und T(s) die Summen aller t(n) und t(s) bezeichnen. Es wird auch aZN · AZN – aZN = aZN : NAa = T(n) : T(s) – T(n).
- ↑ [635] No. 261. S. 434. (Fig. 197.) Setzt man TZ = x, ZA = y, Za = y : TA = rα wie vorhin, α' = α + 1; so ist nach der frühern Proportion. (Bem. 260.) aber y² = r² – x², also y' =
[636]
Hiernach wird
etc.= 0,11869r².Der Halbkreis ist = ½r²π, mithin verhält sich NAn : NeFn = 1,57090 : 0,11869 = 794,1 : 60.
- ↑ [636] No. 262. S. 437. (Fig. 199.) Weil TH² = TS · TK ist, wird SK : ST = SK : = TK · TK : TH² = (TK – TS)TK : TH² = TK² – TH² : TH² = (TK + TK)(TK – TH) : TH² endlich TK : ST = MH · HK : TH².
- ↑ [636] No. 263. S. 437. (Fig. 199.) Setzt man nämlich FG = Y, BG = y, GT = x, HT = h, KT = a; so ist y² = (a² – x²), Y² = a² – x², mithin .
- ↑ [636] No. 264. S. 438. (Fig. 199.) Nach 1. wird nämlich TH : TK = .
- ↑ [636] No. 265. S. 438. (Fig. 199.) Setzet man, wie in Bem. 264. BG = y, FG = Y, TG = x, ferner FTG = β und FTB = α – β = γ; so ist allgemein tang α = , tang β = , tang γ = . Wenn aber [637] HT = b und KT = a gesetzt wird, ist Y = y und y² = (a² – x²), also tang γ = b(a – b). Bezeichnet man nun die, dem grössten Werthe von γ entsprechenden Werthe durch einen Accent, so folgt aus d · tang γ = o, a²b (a + b)x'² = o, also x' = a, y' = b, Y' = a, tang α' = , tang β' = , tang γ' = . Ferner tang α' · tang β' = 1, also α' = 90° – β', = 45° endlich tang γ' = , sin (α' – β') = . Eben so aus tang (α + β) = , sin (α' + β') = und so sin (α' – β') : sin (α' + β') = a – b : a + b = : 1 = sin γ' : 1.
- ↑ [637] No. 266. S. 438. Die mittlere tägliche Bewegung der Sonne ist = 59′8,″3, daher ihre mittlere stündliche Bewegung Δ ☉ = 147″,8. Setzen wir ferner die mittlere stündliche Bewegung der Knoten in den Quadraturen = Δ ♌(q); so haben wir nach Anmerkung 1. Erster Fall, TS : SK = Δ ☉ : Δ ♌(q). Aus der Proportion TH : TK = folgt aber mittelst Gl. 1. TS : TK = 9,0827646 : 40,0827646, TS : SK = 9,0827646 : 1, also Δ ♌(g) = = 16″3. Nach der vorhergehenden Bem. 265. haben wir sin γ' = und da a = KT, b = HT und TK : TH = 19,6524761 : 18,6524761 sin γ' = 1/38,3049522, γ' bedeutet aber nach der vorigen Bemerkung die grösste Bewegung des Knotens in den Octanten, und bezeichnen wir diese stündliche Bewegung durch Δ ♌(o), so haben wir Δ♌(o) = 1° 29′ 45″ ein wenig von dem Werthe im Texte abweichend.
- ↑ [637] No. 267. S. 439. (Fig. 200.) Es ist GT sin GTg = Gg = · sin GPg · gP und &sin GPG : sin GTg = = GT · Pp : Pg², indem Pg = PG gesetzt worden ist.
- ↑ [637] No. 268. S. 440. (Fig. 200.) Setzt man der Kürze wegen die im Zusatz 2 gefundene Veränderung der Neigung während eines Monats = V, so ist V : 33″,2 = AZ · TZ · QAqa : 2Mp · AT² oder : 33″,2 [638] = AZ · TZ · : 2 · AT² und weil Mp die stündliche Bewegung des Mondes auf der Peripherie QAqa ist, die mittlere stündliche Veränderung der Neigung.
Ferner ist unmittelbar = sin PGp, für den Radius = 1 = „ „ „ = AT = sin ATn, = cos ATn, mithin = ½sin ATn · cos ATn = ¼ sin 2 · ATn.
- ↑ [638] No. 269. S. 440. (Fig. 200.) In diesem Falle trifft N mit Q zusammen, es geht daher AZ in AT, TG in TK über und wir erhalten JT · TG = AT · sin pTQ · AT · cos pTQ = ½AT² sin 2pTQ, so wie = AT · sin 2pTQ.
- ↑ [638] No. 270. S. 441. Um die Summe der im Text aufgeführten Sinusse zu finden, wollen wir uns den Quadranten ½π in n gleiche Theile getheilt denken, wo n eine grosse Zahl, hier 1771/6 bezeichnet; alsdann haben wir die Reihe bis zu summiren. Setzen wir nun = x, so wird die gesuchte Summe S = sin x + sin 2x + sin 3x + . + … + sin νx, wo νx = π = π – π, (ν – 1)x = π = π – π. Setzen wir statt der Sinusse die ihnen entsprechenden Exponentialfuncionen, so wird für i = ,
Da aber sin (ν – 1) x = sin (π – π) = sin ; sin νx = sin [639] sin x = sin ; cos x = cos , so wird S = und = . Da nun n sehr gross, also sehr nahe = o vorausgesetzt sind, so kommt der vorstehende Quotient der Form nahe. Um den Grenzwerth desselben für n = ∞ zu finden, setzen wir = k; alsdann geht jener Quotient über in S = d. h. für k = o oder n = ∞, S = wie im Text. Ferner wird = sin 5° 1′ = 874/10000 und 278/10000 · 5878″ = 163″.
- ↑ [639] No. 271. S. 442. Setzt man in §. 38., Zusatz 3. die stündliche Aenderung der Neigung = ν, dort wie hier die Neigung selbst = i, den Winkelabstand der Knoten = Δ; so ist
dort hier ν = · 33″,2 Hh = C sin i sin 3Δ wo r und C constant sind. Mithin sind ν und Hh derselben Grösse sin i sin 2Δ, und wenn sin 2Δ als constant vorausgesetzt wird, sin i proportional: Hh wird daher in gleichem Sinne wie sin i zunehmen.
- ↑ [639] No. 272. S. 444. Der Werth der grössten Mittelpunktsgleichung der Sonne, für den mittlern Abstand der Erde = a, ist im Text = 1° 56′ 20″ = M angesetzt, wobei wir bemerken, dass Hansen a. a. O. M = 1° 55′ 27,″6 hat. Für den Abstand a + x, wird M' = M + Δ'M = M · ; M'' = M + Δ''M = M · also Δ'M : Δ''M = 2 : 3 und Δ''M = 3/2Δ'M. Wenn nun Δ'M die wahre Aenderung von M und Δ''M die hypothetische Aenderung desselben ist, so können wir M + Δ'M = 1° 56′ 20″ oder für M = o, Δ'M = 1° 56′ 20″ setzen und erhalten dann M'' = Δ''M = 3/2(1° 56′ 20″) = 2° 54′ 30″.
- ↑ [639] No. 273. S. 444. Setzt man die grösste Gleichung der mittlern täglichen Bewegung des Apogeums = ΔAp., die des Knotens = ♌, so hat man, auch Hansen a. a. O.
ΔAp. : 2° 54′ 30″ = 6′41,″0 rechtl. : 59′ 8,″3 Δ♌ 3′10,64 rückl. und hieraus ΔAp. = 19′ 43″ rechtl., Δ♌ = 9′ 22″,5 rückl.
- ↑ [640]
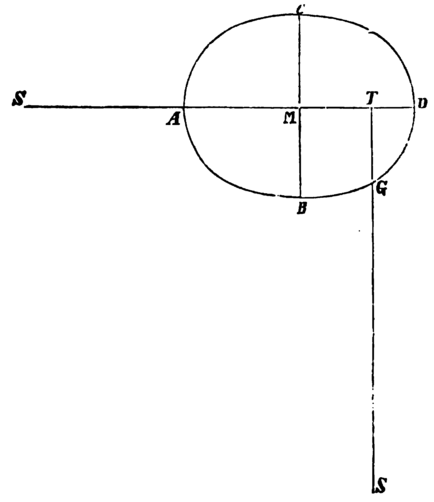
Fig. 264. No. 274. S. 444. Es sei ACDB die Mondbahn, T die Erde, A das Apogeum des Mondes, S die Sonne und deren Abstand von T im Mittel ST = a. Die halbe grosse Axe der Mondbahn sei AM = α, ihre halbe kleine MB = β, die Excentricität MT = αε, also AT = α(1 + ε) und SA = a — α(1 + ε). Ferner wird die Ordinate TG = α(1 - ε²) und SG = a — α(1 - ε²) also TG < AT, SG > AS. Wenn daher der Mond sich im Punkte A befindet, wird die Wirkung der Sonne auf ihn grösser sein, wenn die Sonne sich in der Richtung AD befindet, als die von S ausgehende Wirkung auf den in G befindlichen Mond, wenn die Sonne sich in der auf AD senkrechten Richtung TG befindet und zwar verhält sich die erste Anziehung zur zweiten wie .
- ↑ [640] No. 275. S. 445. Für die Excentricität der Erdbahn = 0,0168 wird der grösste Abstand der Sonne von der Erde = 1,0168, der kleinste = 0,9832; demnach die kleinste Gleichung = = 3' 34,"0, die grösste Gleichung = = 3' 56,"7.
- ↑ [640] No. 276. S. 445. Der für den mittlern Abstand a geltende Werth von 47" ändert sich in demselben Verhältniss, wie in der vorhergehenden Bemerkung und da die in dieser gefundene Aenderung 11" bei 3' 45" = 225" des mittlern Werthes, also etwa 1/20 letztem beträgt, so muss hier 45" um 2" steigen und sinken.
- ↑ [640]

Fig. 265. No. 277. S. 416. Man schlage aus D mit dem Radius DF einen Kreis, alsdann ist E das Apogeum des Mondes und ☾ sein Perigeum. Es sei α das Apogeum der Sonne, P das Perigeum, ☉ der Ort der Sonne.
Nach der Voraussetzung ist dDE = DCB = 2 · ☉E, EDC = 180° — 2 · ☉E, FDE = ☉E — PE. (Voraussetzung im Text), also addirt EDC + FDE = CDF 180° — ☉E = PE. Es ist aber PE☉α = 180°, mithin 180° = ☉E — PE = CDF [641] = α☉ = 360" — α☾PEF☉ und α☾PEF☉ = Winkelabstand ☉ von ihrem Apogeum α = v (wahr. Anomalie ☉), mithin CDF = 360° — v.
- ↑ [641] No. 278. S. 446. Nach Hansen a. a. O. ist die mittlere tägliche Bewegung der Sonne von ihrem Perigeum = 59' 8,"3, die mittlere tägliche Bewegung des Perigeums des Mondes = 6' 41,"0, daher die tägliche mittlere Bewegung der Sonne vom Perigium (Apogeum) des Mondes = 52' 27,"3. Es wird log = 4,55070 und log = 4,55002.
- ↑ [641] No. 279. S. 447. Es wird hier TC = 5505 · sin 12° 18' = 1172,73 und FD = 3/100 · 1172,3 = 35,2.
- ↑ [641]

Fig. 266. No. 280. S. 448. Am grössten wird die, durch die Bewegung des Mittelpunktes der Mondbahn in dem kleinen, zu DF gehörigen Kreise hervorgebrachte Veränderung des Mondortes erscheinen, wenn man die diametral entgegengesetzten Punkte F, F' des Mittelpunktes betrachtet, wo also FDF' diese von T aus gesehene Veränderung unterspannt. Dieselbe wird = Arc sin und da FF' = 70,4; TD = 100000 ist, so ist diese Veränderung = 2' 25".
- ↑ [641] No. 281. S. 447. Aus diesem Grunde hat wohl Tobias Mayer die noch heute in Anwendung kommende Regel aufgestellt, bei der Berechnung der Mondfinsternisse den Durchmesser des Schattens in der Gegend des Mondes um 1/60 zu vergrössern.

Fig. 267. No. 282. S. 449. Es sei TH der Horizont eines Ortes T auf der Erde, S der Ort der Sonne, deren Hohe über dem Horizont STH = h sei, Z das Zenith. Befände sich die Sonne in Z, so würde ihre Kraft P zur Erhebung des Wassers in T nach dem Obigen zu bestimmen sein. Hieraus ergibt sich die längs TS wirkende Seitenkraft, nach dem Parallegramme der Kräfte, TM = P sin TZM = P sin h und hieraus die längs TZ, d. h. nach dem Zenith hinwirkende Seitenkraft TN = TM sin TMN = P sin h². Diese Kraft ist die gesuchte, wenn S nicht im Zenith Z, sondern in der Höhe h über dem Horizont steht. Sie ist daher proportional sin h² = ½(1 — cos 2h) = ½ sinus versus 2h.
No. 283. S. 450. Ein Theil dieses Satzes ist nicht recht klar dargestellt. Die dritte Fluth nach der Syzygie tritt etwa 36 Stunden
| ← Buch III. Abschnitt I. | Nach oben | Buch III. Abschnitt III. → |
| Dieser Text wurde anhand der angegebenen Quelle einmal Korrektur gelesen. Die Schreibweise sollte dem Originaltext folgen. Es ist noch ein weiterer Korrekturdurchgang nötig. |































































































![{\displaystyle \scriptstyle \left.+{\frac {7}{1024}}\cdot {\frac {x^{12}}{r^{7}}}+{\frac {9}{2048}}\cdot {\frac {x^{14}}{r^{11}}}\dots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d829c802659f6dfaff9fd3abae7269d4efb353b)
![{\displaystyle \scriptstyle \times \left[{\frac {1}{\alpha 'r^{2}}}+{\frac {x^{2}}{\alpha '^{2}r^{4}}}+{\frac {x^{4}}{\alpha '^{3}r^{6}}}+{\frac {x^{6}}{\alpha '^{4}r^{8}}}+{\frac {x^{8}}{\alpha '^{5}r^{10}}}+{\frac {x^{10}}{\alpha '^{6}r^{12}}}+{\frac {x^{12}}{\alpha '^{7}r^{14}}}+{\frac {x^{14}}{\alpha '^{8}r^{16}}}\dots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e615c0f5bca0037762e64bb22aaebfe9ccf1257)





































![{\displaystyle \scriptstyle \int \limits _{-r}^{+r}y'dx=r^{2}\left\{{\frac {1}{\alpha '}}\left[2-1+{\frac {3}{20}}+{\frac {1}{56}}+{\frac {1}{192}}+{\frac {3}{1408}}+{\frac {7}{6656}}+{\frac {3}{5120}}\right]\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32ca4b98f31039239f8d35fa41f2fe2e3358460a)
![{\displaystyle \scriptstyle +{\frac {1}{\alpha '^{2}}}\left[{\frac {2}{3}}-{\frac {3}{5}}+{\frac {3}{28}}+{\frac {1}{72}}+{\frac {3}{704}}\dots \right]+{\frac {1}{\alpha '^{3}}}\left[{\frac {2}{5}}-{\frac {3}{7}}+{\frac {1}{12}}\dots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc8ef2cdce62fcf89e76b1942201441df39e569b)
![{\displaystyle \scriptstyle \left.+{\frac {1}{\alpha '^{4}}}\left[{\frac {2}{7}}-{\frac {1}{3}}+{\frac {3}{44}}\dots \right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e32b1382e16d39ddd3514d909ac594a1bc243e7)
![{\displaystyle \scriptstyle =r^{2}\left[{\frac {1,17711}{\alpha '}}+{\frac {0,1917}{\alpha '^{2}}}+{\frac {0,054}{\alpha '^{3}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c649f900cbbb947536e314208e6e32eca47160f0)







































![{\displaystyle \scriptstyle S={\frac {1}{2i}}\left\{\left[e^{ix}+e^{2ix}+e^{3ix}+\dots +e^{\nu ix}\right]-\left[e^{-ix}+e^{-2ix}+e^{-3ix}+\dots e^{-\nu ix}\right]\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dd9b937782cf6cbd2967c667ea9450bb7ce817e)

![{\displaystyle \scriptstyle ={\frac {1}{2i}}{\frac {e^{(\nu -1)^{ix}}-e^{-(\nu -1)^{ix}}+e^{ix}-e^{-ix}-\left[e^{\nu ^{ix}}-e^{-\nu ^{ix}}\right]}{2-\left[e^{ix}+e^{-ix}\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d1ba4440e1cb51a7e872e191498fd639db67a8e)






















