Manuale Mathematicum

Inhalt

Vorrede an den guthertzigen Leser.

Kurtzer Bericht von den Tabulis Sinuum, Tangentium vnd Secantium.

• Erster theil dieses Tractats / in welchem deren hierinn gebrauchten terminorum vnd wörter definition vnd erklärung begriffen.
• Deß Berichts Anderer theil / wie man in dieser Taflen nachschlagen soll.
• Der dritte theil deß Berichts / wie durch hilff nachvolgender Taflen die Triangel zu solviren.
• Taflen / Darinn die genandte Sinus, Tangentes vnd Secantes begriffen

Tetragonische Tafel / sambt bericht / Wie durch hülff derselben / die Quadratwurtzeln auß vorgebenen gevierdten zahlen behend vnd leichtlich zufinden seyen.

• Bericht von der Tetragonischen Tafel.
• Tetragonische Taflen

Cubic Tafeln / Sambt kurtzem vnterricht / wie durch hülff derselben / auß einer vorgebenen Cubischen zahl / die Wurtzel behend außzuziehen seye.

• Bericht vom gebrauch volgender Cubictaflen.
• Cubic Tafel.

---

Manuale Mathematicum, darinn begriffen /

Die Tabulae

Sinuum, Tangentium,

Secantium: so wol die Quadrat-

vnd Cubictafel: sambt gründlichem vnterricht / wie solche nützlich zugebrauchen.

Allen Baw- vnd Kriegsverständigen /

Feldmessern /

vnd andern Kunstliebenden hiebevor in Teutsche Sprach an tag geben /

An jetzo aber wider vbersehen /

vnd auffs New in Truck gegeben Durch Paulum Ledertzen Buchhändlern zu Straßburg.

Vnd Gedruckt durch

Antonium Bertram

M. DC. XIX.

Dem Durchleuchtigen / Hochgebornen

Fürsten vnd Herren / Herren

Friderichen^[1] / Marggraffen zu Baden vnd Hochberg / Landtgraffen zu Sausenberg / Herren zu Rötelen vnd Badenweyler / meinem Gnädigen Fürsten vnd Herren.

Durchleuchtiger / Hochgeborner Fürst / E. F. G. seyen meine vnderthenige dienste / jeder zeit trewes fleisses / gantz gehorsamlich zuvorn / Gnediger Fürst vnd Herr. Nachdem dieses zwar geringfüge Tractätlein von den Tabulis sinuum also abgangen / daß ich dasselbige nicht allein an nötigen orten corrigieren vnd verbessern lassen / sondern auch mit deß autoris gutem vorwissen vnd willen / zum andern mahl auffgelegt: Vnd dann der besondere hochlöbliche vnd rühmliche Lust / Liebe / auch bereits mit besonderm fleiß erlangte wissenschafft Mathematischer Kunst / auffreiss: vnd in grundlegungen der Vestungen vnd wehrhaffter Gebäw / Schantzen vnd anderer darzu gehöriger nothwendigen Kriegsrüstungen / sampt daran hangender Geometrischen Feld: vnd anderer abmessung / jhrer ersprießlichen Vbung vnnd verstendigen Gebrauchs / zu dern E. F. G. gantz geneigt / auch darinnen bereits wol geübt vnd begründet / mich bewegt / solches kleine Büchlein oder Tabulas sinuum, deren verstand / rechter gebrauch vnd nutzbarkeiten / wie nemblich alle winckel vnnd Ecken aller vorfallender Figuren / sonderlich aber der Lehr von Triangeln / die allein das Meisterstuck in solchen Mathematischen wercken ist / zu suchen / zu finden / der linien proportz / lenge / deren inhalt vnd deßgleichen / eigentlich vnd gewiß zuerforschen / zuerlangen vnd zu resolviren: Darbeneben von den Quadrat: vnd Cubic Tafeln / wie darauß so wol der flachen vierungen / als gevierten Corporum die Wurtzel vortheilhafftig außzuziehen / welches dann / neben andern vielen nutzbarkeiten / auch Maßstäbe zum geschütz vnd visierruhten zu machen dienstlich / E. F. Gn. hiermit widerumb vnterthenig zu dediciren / vnd vnter derselben gnedigem patrocinio, Schutz vnd Schirm außgehen zu lassen.

Als ist hiermit mein gantz vntertheniges bitten / E. F. Gn. geruhen solches geringe Wercklin / als die es zu jhrem vorhaben vnd hochrühmlich tragenden lust aller Mathematischen / Mechanischen vnd Militarischen sachen vnd künsten sehr bequem vnd fruchtbarlich befinden werden / auß angeborner Fürstlicher güte vnd gnaden in jhr Fürstlich patrocinium auff- vnd anzunehmen / jhr belieben vnd wol gefallen zulassen / vnd mein gnediger Fürst vnnd Herr zu sein vnnd zu bleiben. Das vmb E. F. Gn. vntertheniges gehorsambs zu beschulden / will ich mir / auff alle zutragende gelegenheit / meines vermögens / trewes fleisses lassen angelegen sein. E. Fürstl. Gn. hiermit Göttlicher Allmacht / zu beständiger guter Leibsgesundheit vnd aller glücklichen Wolfart trewlich / derselben aber zu beharrlichen Gnaden / mich gehorsamlich befehlend. Datum Straßburg den 8. Martij / Anno 1619.

E. F. Gn.

Vnterthäniger vnd gehorsamer

Paulus Ledertz Burger vnd Buchhändler daselbst.

Vorrede an den guthertzigen Leser.

Freundlicher lieber Leser. Vor sieben Jahrn habe ich auff begeren einen geringfügigen bericht von den tabulis sinuum etc. vnd derselben gebrauch / in Teutscher sprach verfertigt / welcher nach dem er gleich ersten Jahrs abgangen / auch seithero vielfältige nachfrag drumben beschehen / bin ich instendig ermahnt worden / solchen andern mahls verbesserter in Truck kommen zulassen. Ob wolen aber nunmehr dergleichen sachen meiner Profeßion nicht seind^[2] / als von denen ich etlich Jahr hero mich abgethan: mich darneben auch billich dieses hett abschrecken sollen / daß es bey voriger edition an Zoilis^[3] nicht gemanglet: Jedoch hab ich solche mühe auff mich zunemmen / mich entlich bereden lassen / vnd den bericht an etlich wenig orten verbessert: insonderheit aber die tabulas auff einen grössern radium, vnd solcher gestalt verfertigt / das verhoffentlich nicht ein eintziger fähler darinnen zu finden sein / vnd also Herr Crüger von Dantzig^[4] nicht mehr vrsach haben wirdt / mir meine errata (die ich zwar selbsten redlich angezeigt / da hergegen andere jhre Bücher bey ehren zubehalten / solche verschweigen) also fleißig nachzuzehlen / vnd in offenem truck vorzuwerffen: da er doch selbst in seinen Taflen derselben nicht wenig begangen / vnangesehen er vermeint / er sey der witzigen Gänse eine / deren nie kein Ey entfallen. In massen dann neben denen vielen erratis / so durch seinen amanuensem^[5] corrigirt worden / noch volgende / vnd so man fleißig suchen wolt / vielleicht noch mehr zufinden / die er auß dieser meiner edition / so es jhme beliebt / corrigiren kan. Als vnder den sinibus 10°.14′. 59°.40′. 63°.21′. 86°.9′. Item vnder den Tangenten, 11°.54′. 52°.33′. 54°.17′. 68°.18′. 81°.16′. vnd vnder den Secanten 11°.31′. 11°.32′. 12°.33′. 38°.8′. 45°.4′. 74°.43′. 75°.27′. 76°.52′. 81°.16′. 81°.19′. 84°.27′. etc. darinnen auch dieses zumercken / das er mir in secante 89°.27′. ein erratum vorwirfft / da doch nicht ich / sondern er selbst geirret. Was Herr Crüger ferners meldet / es seyen keine demonstrationes bey meinem vnderricht / seind dieselben auß der vrsach aussen gelassen / dieweil solcher bericht nicht für seines gleichen Hochgelehrte Leut / sondern allein dem gemeinen / der lateinischen sprach vnerfahrnen Mann zu gutem gestelt worden. Vnd gleich wie in der Arithmetick / deren ebnermassen sehr viel ohne demonstration in Teutscher sprach außgangen / dem gemeinen Mann gnug ist / das er wisse / zum Exempel / man soll in der Regel Detri^[6] das mitlere vnd letzte mit einander multiplicirn / etc: ob er schon nicht weiß / warumb solches geschehe: Also auch ist es meines bedunckens gnug / das ein solcher wisse / es stehen die seiten deß Triangels in solcher Proportion gegen einander / wie die sinus deren einer jeden gegenüberstehenden wincklen / etc. ob er es schon nicht demonstrirn kan. Im übrigen will ich Herr Crügers werck nicht veracht haben: halte dasselb hoch / vnd pflegs auch andern zu commendirn. Bitte allein / er wolle meiner hinfüro schonen / vnd thue dem freundlichen Leser mich zu gunsten befehlen.

Matthias Bernecker.

Kurtzer Bericht von den

Tabulis Sinuum, Tangentium vnd Secantium.

Vnder allen flachen Figuren ist der Triangel die erst vnd vornembste / als in welche all andere mehrseitige flechen resolvirt werden / vnd darauß entspringen. Dannenhero die lehr von den Trianglen vnd jhrer dimension wol für den kern der Geometrei zuhalten / ohn welche weder die vbrigen theil der Geometrei / noch andere von derselben herrührende Künste / als Geodaesia, Optica, Dioptrica, Meteoroscopica, Gnomonica, Geographia, Astronomia, Musica, etc. gründtlich erlernt werden mögen.

Es beruhet aber die dimension der Triangel auff dreyen stucken. Dann in denselben entweder die seiten / oder winckel / oder fleche gemessen werden.

Die abmessung der fleche betreffend / weil sie auch mit andern Figuren gemein / vnd dem Triangel nicht eigenthumblich zugehöret / sondern von den quadrangulis entlehnet wirdt / wie auß der 41. vnd 42. proposition deß ersten Buchs Euclidis zusehen: wirdt allhie außgelassen / vnd allein gelehrt / wie die seiten vnd winckel deß Triangels zumessen seyen: welches dann geschicht durch die Regel Detri, die da lehrt / wie man von vieren vntereinander proportionirten zahlen / so die drey bekandt / die vierdt vnbekandte soll erforschen: deren fundament ist in der 16. Prop. deß 6. Buchs Euclidis.

Dahero vonnöten / das die winckel vnd seiten / als theil deß Triangels / in gewisser proportion gegen einander stehn / vnd mit einer bekandten zahl müssen außgesprochen werden können.

Solche proportion aber (weil aller winckel mensur ein Circkeltrumm oder krumme lini ist / so auß dem spitzen deß winckels / als Centro / gerissen wirdt zwischen beyden linien / so den winckel einschliessen: vnd man aber bißhero kein gewisse proportion der krummen linien gegen den geraden erfunden hat / auch vielleicht nimmer finden wirdt) kan man nicht wissen / es sey dann / das an statt gemelter krummen linien / als mensurn deß winckels / andere gerade zu dem Circkel appliciert / vnd deren grösse / so sie gegen dem halben Diameter desselben Circkels haben / gegeben werde. Solche gerade linien nun / die zu dem Circkel appliciert / vnd an statt der krummen masse deß winckels genommen werden, seind nichts anders / als die also genante Sinus, Tangentes vnd Secantes, von welchen in volgender kürtzen instruction dergestalt soll gehandlet werden. Erstlich sollen die termini vnd wörter / so in dieser lehr gebreuchlich / beschrieben vnd erkläret: Zum andern / wie man die tabulas Sinuum etc. gebrauchen / vnd darinn nachschlagen soll / gewiesen: Endtlich gelehret werden / wie man alle vnd jede vorgebene Triangel auß gemelten tabulis solvirn, vnd jhre so wol seiten als winckel erforschen soll.

Erster theil dieses Tractats / in welchem

deren hierinn gebrauchten terminorum

vnd wörter definition vnd erklärung begriffen.

1. Ein jede Circumferentia, Cirkelrunder riß / oder Circkellini wirdt getheilt in 360. gleiche theil / so man gradus nennet: vnd 1. gradus wirdt widerumb in 60. scrupula prima oder erste minuten: 1. scrupulum primum in 60. scrupula secunda oder andere minuten: 1. scrupulum secundum in 60. scrupula tertia oder dritte minuten / vnd also fort / eingetheilt: wiewol man in gemeinem gebrauch nicht so genaw sucht / vnd es gemeiniglich bey ersten / oder auffs höchst andern minuten bewenden lasset: Deren Logistische bezeichnuß ist / das man ob den graden ein nulla / ob den ersten minuten ein ablang strichel / ob den andern minuten zwey solche strichel / vnd also fortan setzet. Zum Exempel / 16. grad / 23. erste minuten / 7. anderte / 51. dritte / werden also geschrieben: 16°.23′.7″.51‴.

2. Arcus, ein Bogen / ein Cirkeldrumm / wirdt genennet ein stuck oder theil der circumferentz: dergleichen vielerley / vnder welchen aber der Semicirculus vnd Quadrans die vornembsten seind.

3. Semicirculus wirdt genennet die halbe circumferentz, 180. grad in sich haltend. Als da ist GFC. in nachfolgender Figur.

4. Ein Quadrant ist der vierdte theil der circumferentz / 90. grad begreiffend. Als FBC. oder FIG.

5. Complementum, ein ergentzung oder erfüllung / ist der jenige arcus, so dem vorhabenden arcui, noch abgeht /

das er nicht gar ein Semicirculus,^[7] oder ein Quadrant seye. Ist also das complementum zweyerley. 1. Dann wann der auffgebene oder vorhabende arcus kleiner ist / als 90. grad / oder ein quadrant, so wirdt sein complementum genennet das jenige Circkeltrumm / so jhme an 90. graden noch fehlet.

Als deß arcus BC. 50°. complementum ist der arcus FB. 40°. Vnd hergegen deß arcus FB. 40°. complementum vnd abgang an einem quadranten ist der arcus BC. 50°.

2. Wann aber der vorhabende arcus grösser ist / als ein quadrant, so wirdt der jenige arcus, welcher jhme an dem Semicirculo oder an 180. graden noch abgehet / sein complementum genennet. Als in diser figur / deß arcûs CBFI. 130°. complementum ist der arcus IG. 50°. Wirdt also das erste complementum erkündigt / so man den vorgebenen arcum von 90°. das andere aber / so man jhn von 180°. abziehet. Als wann 36°.12′. von 90°. subtrahirt werden / bleiben 53°.48′. welches ist sein complementum, vnd abgang vom quadranten. Item wann man 121°.17′.51″. von 180°. abziehet / bleibt sein complementum vnd abgang vom Semicirculo, 58°.42′.9″.

6. Ob ein vorhabender winckel rectus, acutus oder obtusus,

vnd wie groß er sey / wirdt erkandt / wann man deß Circkels einen fuß auff die spitz deß winckels setzet: vnd mit dem andern beweglichen fuß ohngeferd auß einander gestreckt / einen arcum oder Circkeltrumm / zwischen den zweyen zusammenlauffenden linien reisset / vnd sihet / wie viel grad derselbe arcus halte von dem gantzen Circkelriß. Dann so bemeltes Circkeltrumm ein quadrant oder viertel der gantzen Circkellini ist / so ist der vorhabende winckel ein angulus rectus, oder ein rechter Winckelhack. So aber gedachtes Circkeltrumm kleiner ist / als ein quadrant, so wirdt solcher winckel angulus acutus, ein enger oder spitziger winckel genennt. Wo entlich das Circkeltrumm grösser sein wirdt als ein quadrant, so ists angulus obtusus,ein weiter oder stumpfer winckel. Daher zusehen / das alle anguli recti einerley / vnd allezeit von 90. grad: die acuti vnd obtusi aber vielerley seyen / vnd mehr oder weniger grad offenstehn.

Als AEB. ist ein rechter winckel / dann sein mensur der arcus AB. ist ein viertel deß Circkels / wann er gantz außgerissen were. Item DEC. ist ein spitziger winckel / dessen grösse allhie ist 36°. wie der arcus DC. außweist. Vnd CEA. ist ein stumpffer winckel / 144°. eröffnet: dann so groß ist allhie sein mensur / der arcus CBA.

7. Die winckel haben auch jhre complementa, nicht anders als droben von den arcubus gemeldet worden. Als in nechster Figur / deß spitzigen winckels CED. 36°. complementum vnd abgang vom quadranten ist der winckel CEB. 54°. Item deß stumpffen winckels AEC. 144°. complementum vnd abgang vom halben circkel / ist der winckel CED. 36°.

8. Chorda ein saiten / ein sennen / ist ein gerade lini / so in einem Circkelrunden riß mit beyden orten anrüret / vnd den gantzen circkel in zwey segmenta oder stuck theilet / welche sie beyde subtendirt. Daher sie sonsten subtensa, das ist / ein vnderzogene lini: Item inscripta, ein lini in den circkel gerissen / genennet wirdt. Die gröste chorda eines jeden Circkels ist sein diameter, mittelriß / oder durchzug durch das centrum oder mittel punct lauffent / so den Circkel in zwey gleiche segmenta, nemblich in zwen semicirculos theilet.

Als in dieser Figur ist / GC. oder FH. Durch die andern chordas aber alle wird der Circkel in zwey vngleiche segmenta getheilet / deren eins grösser / das ander kleiner ist / als ein semicirculus. Als die chorda IB. subtendirt auff der einen seiten den kleinern arcum IFB. auff der andern den grössern IHB.

9. Sinus, ist ein gewisser theil von der chorda, dessen seind etliche arten / welchen diese beschreibung allen gemein ist. Als /

10. Sinus rectus, ein rechter sinus, ist der halbe theil von der chorda deß gedoppelten arcûs. Als in nechster figur der sinus rectus deß arcûs BC. 50°. ist die linea BE. Dann gemelter arcus BC. gedoppelt / ist der arcus BCD. dessen chorda oder vndergezogene lini ist BED. deren halber theil ist BE. welcher halbe theil dann / wie gemelt / der sinus rectus deß vorhabenden arcus BC. ist. Oder / noch deutlicher zusagen / sinus rectus ist ein perpendicularis linea, das ist / ein waglini / so wagrecht / winckelrecht oder bleyrecht von dem einen ende deß vorhabenden arcûs herab fallt auff den diameter / so auß dem andern ende desselben arcûs gezogen wirdt. Als in vorigem Exempel der sinus BE. fallt wagrecht auff den diameter GC. Das fundament diser beschreibung steckt in der 3. prop. deß 3. Buchs Euclidis.

11. Sinus versus, ein verkerter sinus, ist ein segmentum oder stuck deß diameters / zwischen dem sinu recto vnd der circumferentz eingeschlossen. Als / sinus versus deß arcûs BC. ist EC. wirdt sonsten sagitta oder ein pfeil genennet / deme er sich der figur nach vergleicht.

12. Sinus complementi ist der jenige sinus rectus, welcher gebürt dem complemento deß vorhabenden arcûs. Als BK. ist deß auffgebenen arcûs BC. sinus complementi. Dann arcus BF. ist das complementum deß arcûs BC. wie droben in der 5. definition zusehen: welchem complemento gebürt gedachter sinus rectus BK. Hiebey ist wol zumercken / das der sinus complementi allezeit gleich seye dem segmento oder stuck deß diameters / welches da ist zwischen dem centro vnd sinu recto deß vorhabenden arcûs. Als / sinus rectus deß complementi BF. nemblich die lini BK. ist in gleicher grösse mit der linien EA. wie auß der 34. proposition deß 1. Buchs Euclidis zusehen. Derwegen eines für das ander gebraucht wirdt / wie hernach im drittem theil offt wirdt vorkommen.

13. Sinus totus, vel maximus, der gantze oder gröste sinus, ist der sinus eines quadranten, vnd ist allezeit der halbe diameter. Als FA. ist der sinus deß quadranten FBC. Dieser wirdt sonsten Radius genennet / Metaphorischer weiß. Dann gleich wie radius, das ist / ein Speiche deß Rads / auß der Nab in die Felge geht: also wirdt sinus totus auß dem mittelpunct biß zu der circumferentz gezogen.

Es wirdt aber der Radius, als der Hauptsinus / in etlich gewisse gleiche theil abgetheilet / vnd eben in solchen theilen auch die andern sinus, tangentes vnd secantes gegeben. Als in vnserer Tafel wirdt der radius genommen von 10000000. theilen: vnd eben in dergleichen Partickeln die vbrigen zum Circkel applicirte linien angezeigt. Nicht ohn ist / weil fast alle sinus, tangentes vnd secantes gegen dem radio irrational seind (dessen vrsach Ramus^[8] elem. 8. lib. 12. seiner Geometrei anzeigt) das man sie nimmermehr alle exactè geben kan: aber doch kan man sie so weit haben / das an allen vnd jeden zahlen in der Tafel gesetzt / auch nicht ${\tfrac {1}{10000000}}.$ deren theilen / die der radius hat / manglen thut / welches dann keinen mercklichen jrrthumb bringen kan.

14. Tangens, ein berührende lini / ist die jenige / so

perpendiculariter vnnd bleyrecht auffgerichtet ist an dem ende deß diameters bey dem einen ort deß vorhabenden arcûs, vnd geht biß zu der secante, welche auß dem centro durch das ander ort desselben arcûs gezogen ist.

Als LC. ist die Tangens deß arcûs BC. wirdt darumb also genennet / weil sie die circumferentz nur berühret / vnd nicht durchschneidet. Von andern wirdt sie geheissen Prosinus, vorsinus / dieweil sie vor dem sinu steht / vnnd gegen demselben parallel, das ist / in gleicher weit stehent: Item Adscripta, ein hinzu gerissene lini: weil sie an / vnd nicht durch die circumferentz gezogen wirdt. Die tabula Tangentium wirdt sonsten tabula Adsctiptarum. Item tabula Faecunda genennet.

15. Secans, ein schneidende lini / ist die / so auß dem centro vberzwerch durch das eine ort deß vorgebenen arcûs hinauß biß zu der Tangente gezogen wirdt. Als AL. ist die Secans deß arcûs BC. Diese wirdt von andern genennet hypotenusa, oder subtendens, weil sie einen rechten winckel (als hie LCA.) subtendiret, vnd gegen demselben vber stehet: Item Transinuosa, ein lini / so vberort / vber den sinum rectum gezogen wirdt. Die Tafel der secantium wirdt sonsten genennet tabula hypotenusarum, Item tabula benefica.

Deß Berichts Anderer theil / wie

man in dieser Taflen nachschlagen soll.

Es seind die sinus, tangentes vnd secantes in folgenden Tafeln nit weiters / als auff einen quadranten oder 90. grad verzeichnet / auß vrsach / weil die arcus, so grösser seind als ein quadrant, gleiche sinus haben mit den kleinern.

Als die lini BE. ist so wol sinus deß grössern arcûs BFIG. als deß kleineren BC. So können gemelte grössern arcus gantz keine Tangentes vnnd secantes haben / wie auß obgesetzter 14. vnd 15. definition abzunemen.

Diser Tafeln nun sich recht zu gebrauchen / ist vonnöten / das vorher jhr disposition vnd structur wol verstanden werde: die ist also beschaffen.

Zur lincken seiten der Taflen finden sich die sinus, tangentes, vnd secantes der jenigen graden / so vnter einem halben quadranten, das ist / von 1°. biß 45°. begriffen: zur rechten seit aber die jenigen so drüber / vnd von 45°. biß 90°. auffsteigen / dergestalt / das zur lincken hand die grad zu öberst mit etwas grössern ziffern / vnd nebens abwertz jhre erste minuten mit kleinen ziffern: bey der Rechten hand aber die grad zu vnderst / auch mit gössern ziffern / vnd dann auffwertz die ersten minuten mit kleinern ziffern gesetzt werden: Vnd solches darumb / damit / es werde was da woll für ein arcus angeben / man gleich darneben auff der andern seit sein complement, vnd demselben gehörigen sinum, tangentem vnd secantem haben möge.

Es besteht aber der gebrauch dieser Taflen auff zweyen stucken: das nemblich entweder eines jeden vorgebenen arcûs, so kleiner / als ein semicirculus ist / gebürender sinus, tangens, secans: oder aber hingegen / eines jeden vorgebenen sinûs, tangentis, secantis gebürender arcus darauß genommen werde: wie solches auß folgenden Reglen weiters zu vernemmen: in welchen / was von dem sinu gesagt wirdt / alles ebenmessig von der tangente vnd secante zu verstehen ist.

1. Regel.

Den sinum eines vorgebenen arcûs

von graden vnd ersten minuten zufinden.

Ist der vorhabende arcus vnter 45°. so wirdt zur lincken: wo darüber / zur rechten hand gesucht. Zum Exempel der arcus sey 32°.17′. dessen sinum zusuchen / nim die 32°. oben zur lincken: vnd in derselbe zeilen abwertz die 17′. fahr als dann vberzwerch gegen der rechten / so wirstu den begerten sinum 5341064. finden.

Item es sey der vorhabende arcus 62°.26′. Nim die 62° vnten zur rechten hand / vnd in derselben zeil auffwertz die 26′. fahre von den minuten vberzwerch gegen der rechten hand / so wirstu finden den begerten sinum 8864730.

Hiebey ist zu mercken / wann nur gradus vnd keine minuten darbey geben werden / so muß man nemen den vorhergehenden grad vnd 60′. Als der sinus für 27°. wirdt gesucht vnter 26°.60′. vnd ist 4539905.

Doch ist diß zuverstehn nur von den jenigen graden / die oben auff zur lincken stehn / vnd vnter dem halben quadranten 45°. seind. Die andern grad aber vber 45°. so vnten zur rechten stehn / werden völlig genommen. Als der sinus 76°. wirdt gesucht vnter 76°.0′. vnd ist 9702957.

2. Regel.

Wann ein arcus, neben den graden

nicht allein erste / sondern auch anderte minuten hette / wie dessen sinus zufinden.

Die Taflen seind allein auff grad vnd erste minuten gericht: so aber auch anderte minuten vorkommen / muß pars proportionalis gesucht / vnd zu dem sinu deß nechst kleinern arcûs addirt werden / wie solchs auß dem exempel deutlich zuverstehn.

Es seye der sinus deß arcûs 16°.38′.20″. zusuchen. Erstlich nim den sinum deß nechst kleinern arcûs 16°.38′. nemblich 289458. deßgleichen nim den volgenden sinum deß nechst grösseren arcûs 16°.39′. nemblich 2865245. subtrahir jenen sinum von diesem / restirt die differentz oder vnderscheid beeder sinuum 2787. Procedir ferners also nach der Regel Detri, vnd sage: die differentz beeder arcuum, 16°.38′. vnd 16°.39′. nemblich 60″. (oder 1′.) gibt mir die differentz jhrer sinuum 2787. was werden mir geben 20″?

60	————	2787	————	20
3				1
		2
		2787	929
		333

Kommen mir 929. welches wirdt genennt pars proportionalis, das ist / ein proportionirter theil / weil er gegen 20″. eben in der proportion steht / wie 2787.^[9] gegen 60″. Diese 929. nun müssen zu dem gefundenen kleinern sinu, als 2862458. addirt werden: so ist die Summa 2863387. als der eigentliche sinus deß vorhabenden arcûs 16°.38′.20″.

3. Regel.

Eines vorgebenen arcûs complementum vnd seinen sinum zufinden.

Das complementum eines arcûs kan zwar (wie droben in der 5. definition gemeldet worden) durch subtraction von 90°. in den Taflen aber viel leichter / vnd stracks darneben auch sein sinus gefunden werden.

Es seye der vorhabende arcus 41°.52′. den suche zur lincken / vnd von den 52′. fahre gegenüber vnder die minuten zur rechten / da findestu 8′. vnd gleich darunder 48°. Ist also das complementum 48°.8′. dessen sinus 7446999. wirdt gesucht allermassen / wie droben in der ersten Regel gelehrt worden

Item es werde gegeben der arcus 72°.40′. dessen complement zusuchen / so fahre von den 40′. zur rechten / stracks gegen vber zur lincken / da stehen 20′. vnd oben 17°. Ist also sein complementum 17°.20′. dessen sinus 2979303.

4. Regel.

Wie sinus versus zu finden.

Subtrahiere den sinum complementi von dem Radio oder halben Diametro: der rest ist sinus versus. Als in der Figur droben am 10. Blat deß arcûs BC. 50°. sinum versum DC. zu suchen / so subtrahiere den sinum complementi 40°. BK. (das ist / AE. Dann diese 2. linien einander gleich / wie droben in der 12. definition gemeldet worden) nemblich 6427876. von dem Radio AC. 10000000. so bleibt sinus versus EC. 3572124.

5. Regel.

Wie der arcus eines vorgebenen sinus recti zu erkündigen.

Der sinus wirdt in der Tafel gesucht / vnd gleich darneben zur rechten oder lincken der jhm respondierende arcus in graden vnd minuten genommen. Als der sinus 3974148. in der Tafel gesucht / gibt mir zur lincken den arcum 23°.25′. Item der sinus 9112835. gibt nur zur rechten / den arcum^[10] 65°.41′.

Ob man aber zur lincken oder rechten hand suchen soll / wirdt darauß abgenommen. Ist der vorhabende sinus kleiner als 7071068. (welches ist der sinus deß halben quadranten 45°.) so sucht man jhn sambt seinem arcu zur lincken: wo grösser / zur rechten hand.

Also auch wann die tangens kleiner / als 10000000. Item die secans kleiner ist als 14142136. so werden sie / vnd die jhnen respondierende arcus, zur lincken: wo grösser / zur rechten genommen.

Wann der vorhabende sinus nit eben gar eigentlich in den Taflen steht / so nimbt man deß nechst kleinern oder nechst grössern seinen arcum. Dann ob wol solches nit eben praecisè der rechte arcus ist / fählet er doch nit gar vmb ein erste minut / welches kein mercklichen irrthumb verursachen kan. Als 7087622. ist zwar nit eben genaw vnder den sinibus zufinden: derwegen der arcus deß nechst kleinern sinûs 7087504. nemblich 45°.8′. zu nemen ist.

Wann man aber je gar genaw auch mit anderten minuten den arcum suchen wolte / so wirdt widerumb pars proportionalis gesucht / vnd damit procedirt / wie volgendes Exempel außweiset. Der sinus seye 2863480. dessen arcus zusuchen ist. Weil man aber solchen sinum nit praecisè findet / so nimbt man den nechst kleinern vnd nechst grössern / nemblich 2862458. vnd 2865245. jener von diesem subtrahirt / gibt beeder differentz 2787. welche hernach in der Regel Detri, vornen gesetzt wirdt. Darnach subtrahirt man auch den nechstkleinern sinum 2862458 von dem vorhabenden 2863480. ist die differentz 1022. welche in der Regel zu letzt gesetzt wirdt. In der mitten aber stehen allezeit 60″. (oder 1′.) als nemblich die differentz beeder arcuum, so dem nechst grössern vnd nechst kleinern sinui gebüren. Wirdt derhalben also concludirt 2787. geben 60″. derhalben werden 1022. geben 22″. welches ist pars proportionalis.

2787	—————	60″	—————	1022.
				${\tfrac {60}{61320}}$
	5586
	61320	22″.
	27877
	278

Diese 22″. addiere man zu dem arcu, der dem nechst kleinern sinui 2862458. respondiret / nemblich zu 16°.38′. werden 16°.38′.22″. welches ist der eygentliche arcus dem vorgebenen sinui 2883480. gehörig.

6. Regel.

Wie der arcus eines vorgebenen sinûs versi zu erkennen.

Subtrahire den sinum versum vom radio: der rest ist sinus complementi. Dises complementi sein arcus ist der begerte. Als wann gefragt würde / 3572124. EC. sinus versus, (besihe die Figur am 10. blat) was für einen arcum er habe / ziehe jhn ab vom Radio AC. 10000000. bleibt 6427876. AE. oder BK. sinus deß complementi FB. 40°. Dieses complements FB. arcus ist BC. 50°. so dem auffgebenen sinui verso respondiret.

7. Regel.

Wie die chorda eines jeden vorgegebenen arcûs zufinden.

Der auffgebene arcus ist entweder kleiner als ein halber circkel 180°. oder grösser. Ist er kleiner / so halbiere jhn / nim auß der Tafel den sinum rectum dises halben theils / den dupliere / so hastu die chordam deß gantzen arcûs.

Als es wirdt begert / die chordam deß bogens BCD. 100°. zu finden in solchen theilen / dergleichen der radius 10000000. hat. Der halbe theil dieses bogens ist BC. 50°. dessen sinus rectus BE. 7660444. gedoppelt / gibt die lini BED. 15320888. welche ist die chorda deß bogens BCD.

Im fall aber der vorgebene arcus grösser were / als der halbe circkel 180°. so subtrahir jhn von dem gantzen circkel 360°. deß rests chordam such allermassen / wie oben gelehrt. Als es wirdt begert (besihe die vorhabende figur) die chorda deß grössern bogens BGD. 260°. den subtrahier von 360°. bleibt der kleinere bogen BCD. 100°. dessen obgefundene chorda BED. 15320888. ist auch die chorda deß grössern vorgebenen bogens BGD. wie droben auß der 8. definition zusehen.

8. Regel.

Wie hingegen der arcus einer jeden vorgegebenen Chordae zufinden.

Die operation kan auß voriger Regel / vnd volgendem Exempel erlernt werden. Es wirdt gefragt / was die vorgebene chorda BED. 15320888. für einen bogen subtendiere. Ihr halber theil ist BE. 7660444. dieser / nach der 5. Regel in den tabulis sinuum gesucht / gibt den bogen BC. 50°. welcher gedoppelt / gibt den gesuchten arcum BCD. 100°. so anders außgedingt worden / das der arcus solle kleiner sein / als ein semicirculus: solte er aber grösser sein / so subtrahiere gemelte 100°. von 360°. rest 260°. welchs ist der grössere begerte arcus BGD.

Der dritte theil deß Berichts / wie

durch hilff nachvolgender Taflen die Triangel zu solviren.

Ehe vnd dann von der resolution jeder triangel insonderheit gehandlet wirdt / muß vorher die 32. proposition deß 1. Buchs Euclidis wol in acht genommen werden / als welche in volgender instruction offt vorkommet. Darinnen wirdt gelehret / das in einem jeglichen triangel die drey wickel zugleich / sie seyen wie sie wollen / allezeit zwen Rechte winckel / das ist 180°. grad thun.

Als in dem triangel ABC. wann der winckel A. 41°.10′. Item der winckel B. 108°.2′. vnd C. 30°.48′. zusammen addirt werden / so machen sie gerad 180°. oder zwen angulos rectos. Vnd also in allen andern trianglen.

Darauß folget dann /

1. Das in einem jeden triangel nicht mehr / als ein einiger Rechter / oder auch stumpffer winckel sein kan.

2. Der dritte winckel ist allezeit der andern zweyen jhr complementum oder abgang vom semicirculo. Dannenhero / wann in einem triangel die grösse zweyer winckel bekandt ist / man darauß alsbald auch deß dritten vnbekandten winckels grösse erforschen kan / durch subtraction von 180°.

Als der winckel C. ist der andern zweien A. vnd B.^[11] complement zum semicirculo. Vnd also wann A. 60°. vnd B. 84°. bekandt / C. aber vnbekandt were: so addier jehne zwen / werden 144°. Diese summ subtrahir vom semicirculo 180°. bleiben 36°. welches ist die grösse deß gesuchten winckels C.

3. In einem rectangulo oder winckelrechten triangel ist allezeit der eine spitzwinckel deß andern complement vnd abgang zum quadranten: vnd kan derwegen / so der eine spitzwinckel bekandt / durch abziehung dessen von 90°. auch der andere bekandt werden.

Als in dem triangel ABC. am 24. blat / wann der acutus A. 36°.52′. bekandt / vnd von 90°. abgezogen wirdt / bleibt sein complement 53°.8′. welches ist der andere acutus B.

Damit nun zur Hauptsache geschritten werde / ist zu wissen / das in einem jeden triangel / sechs ding seyen / nemblich drey seiten / vnd drey winckel: auß welchen 6. stucken / so drey bekandt / können allezeit auch die vbrigen noch vnbekandte drey durch anleitung nachvolgender Reglen erkundiget werden: außgenommen in dem einigen casu, so nur die drey winckel bekandt weren. Dann darauß kein seite kan erforscht werden: sintemal drey winckel eines triangels dreyen wincklen eines andern triangels gantz gleich sein können: da doch beeder seitten einander gantz vngleich.

Als beede triangel ABE. vnd ACD. seind / was die winckel anlangt / allerdings gleich (wie

auß der 29. proposition deß 1. Buchs Euclidis zusehen) die seiten aber betreffent / vngleich: vnd also diese auß jehnen nit zu erfahren.

In andern casibus aber allen / wie gemeldt / kan man auß dreyen vorgebenen oder bekandten stucken / andere drey vnbekandte / als auß zweyen wincklen vnd einer seit / den dritten winckel vnd vbrige zwo seiten: oder auß zweyen seiten vnd einem winckel / die dritte seit vnd andere zwen winckel: oder auß allen drey seiten alle drey winckel durch die Regel Detri vnd diese Taflen erfahren / in massen auß volgenden Reglen vnd beyfügten Exemplen zuvernemmen.

1. Regel.

Wann in einem triangulo rectangulo,

oder winckelrechtem triangel / die zwen winckel (vnd also auch der dritte / als der jehner zweien complement ist) zusambt einer seiten bekandt seint / wie man darauß die vbrigen zwo vnbekandte seiten erfahren solle.

Nachdem zwo arten der triangel seind / Als 1. Rectangulum, so einen rechten / vnd zwen spitzwinckel hat: 2. Obliquangulum, von schlimmen wincklen / darinnen entweder ein winckel obtusus oder stumpff / die andern zwen acuti vnd spitzig: oder aber alle drey spitzig seind: ist vnter jhnen die erste art am vornembsten vnd gebreuchlichsten. Dahero auch rectangulum Magister Matheseως, ein Meister der Mathematischen künste genennet wirdt.

Dessen resolution ist vmb so viel desto leichter / als anderer triangel / dieweil darinnen ein jede vnter den dreyen seiten / für den Radium oder sinum totum genommen / vnd also ein einiger triangel auff dreyerley art solvirt werden kan.

Als der einige triangel ABC. wirdt auff dreyerley weiß zu dem Circkel appliciert. Dann erstlich wirdt die hypotenusa (das ist / die lini / so vberort geht / vnd vber den rechten winckel gestreckt ist) nemblich die lini AB. für den Radium genommen: vnd seind alsdann die andern zwo seiten / so den rechten winckel C. einschliessen / die sinus dero gegen jhnen vberstehenden spitzwincklen. Als BC. ist sinus deß winckels A. vnd AC. ist sinus deß winckels B. als da geschicht in beygesetzter ersten figur.

Zum andern kan die Basis, (das ist / die vnderst / oder grundlini / darauff das rectangulum steht) nemblich die lini AC. an statt deß Radij genommen werden. Vnd ist alsdann BC. die Tangens, vnd AB. die Secans deß winckels A. Wie in der andern figur zusehen.

Zum dritten kan auch Cathetus, (das ist / die gesenckte lini / die auffrecht oder wagrecht seiten deß winckelrechten triangels / welche einen rechten winckelhacken mit basi machet) nemblich die lini BC. Radius sein: Vnd ist alsdann AC. die Tangens, vnd AB. die Secans deß winckels B. als erscheint auß der dritten figur.

Welches dann auß der vrsach wol zumercken / damit man zu vermeidung der beschwerlichen division / allezeit nach beschaffenheit der auffgebenen Frag / den Radium zu anfang in die Regel Detri setzen möge.

Es hat aber diese Regel zwen Casus. Dann neben den dreyen wincklen entweder die hypotenusa: oder aber eine auß den zweyen seiten / so den rechten winckel beschliessen / bekandt / vnd darauß die andern zwo vnbekandten seiten zuersuchen seint.

Vom ersten Casu.

Im jetzt gemeldtem triangel ABC. werden als bekandt genommen erstlich zwen winckel / nemblich der rectus C. so allzeit 90. grad helt / vnd der eine acutus A. 36°.52′. durch dessen abziehung dann von 90°. auch sein complement / als der dritte winckel B. 53°.8′. bekandt wirdt. Zum andern wirdt auch als bekandt angenommen die hypotenusa AB. 15. schuch: vnd begert / auß diesen datis oder bekandten dingen / die zwo noch vnbekandte seiten AC. vnd CB. zuerkundigen. Welches auff dreyerley weiß geschehen kan / nach deß triangels obgemelter dreyerley application.

Vnd erstlich zwar die seite CB. zuerkundigen / schliesset man nach der ersten application also:

Wie sich verhelt der Radius AB. 10000000. gegen BC. 5999549. (welches ist der sinus deß winckels A. 36°.52′.) Also verhelt sich auch die seit AB. 15. schuch / gegen der seiten BC. 9. schuch.

(NB. Die brüch so in diesem vnd volgenden Exempelen vorkommen / werden kürtze halben / vnd weil sie keinen mercklichen jrrthumb bringen / außgelassen.)

Oder nach der anderten application / also:

Wie sich verhelt deß winckels A. 36°.52′. sein secans AB. 12499471. gegen seiner Tangente BC. 7499119. Also verhelt sich die seite AB. 15. gegen der seiten BC. 9.

Oder nach der dritten also:

Wie sich verhelt AB. 16667920. (die Secans deß winckels B. 53°.8′.) gegen dem Radio BC. 10000000. Also verhelt sich die seite AB. 15. gegen der seiten BC. 9.

Kombt also nach all dreyen arten einerley facit. Es ist aber die erste am füglichsten / weil der Radius zu anfang in der Regel Detri steht / vnd also lange division verhüttet wirdt / dabey dann sonderlich auch dieser vortel / das man zu vermeidung der brüch / ohne weitere nachrechnung / neben den gantzen schuhen alsbald auch derselben zehentheilige zoll vnd minuten haben kan / davon drunden kurtze andeutung geschehen soll.

Ebenmeßig die seite AC. zuerkundigen: schliesset man auff dreyerley weiß / nach gestalt der drey obgemelten applicationen deß vorhabenden triangels ABC.

1. applic.)		$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Radius BA. 10000000.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	gegen dem	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Sinu AC. oder BD. 8000338.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	Also verhelt sich die seite BA. 15. schuch / gegen der seite AC. 12. schu.
2.)	Wie sich verhelt		Secans BA. 12499471.				Radi AC. 10000000
3.)			Secans BA. 16667920.				Tangente AC. 13334900.

Vnter welchen dreyen modis auch der erste am füglichsten / wegen erst angezeigter vrsach.

Vom anderten Casu.

Im fall aber neben den wincklen / auch eine auß den jenigen seiten / die den rechten winckel einfassen / bekandt were / vnd die andern zwo vnbekandt: wirdt solcher gestalt procedirt. Vnd erstlich zwar soll die bekandte seiten sein AC. 12. schuch. Darauß ich nach obgemelten dreyerley applicationen deß fürhabenden triangels ABC. also schliesse:

1. applic.)		$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Sinus CA. 8000338.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	gegen dem	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Radi. AB. 10000000.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	Also verhelt sich die bekante seit CA. 12. schuh gegen der hypotenusa AB. 15.
2.)	Wie sich verhelt		Radi. CA. 10000000.				Secante AB. 12499471.
3.)			Tangens CA. 13334900.				Secante AB. 16667920.

Item die andere seiten BC. wirdt auß vorhabenden datis also gesucht.

1.)	Wie sich verhelt.	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Sinus AC. 8000338.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	gegen dem	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Sinu CB. 5999549.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	Also verhelt sich die bekante seit AC. 12. schuh gegen der seiten CB. 9. schuh.
2.)			Radi. AC. 10000000.				Tangente CB. 7499119.
3.)			Tangens AC. 13334900.				Radio CB. 10000000.

Allhie vnd im vorigen ist der andere modus der beste vnd leichtiste.

Zum andern / soll die bekandte seiten sein BC. 9. schuch / darauß neben den andern datis widerumb auff dreyerley weiß gesucht wirdt / Erstlich die seite AB. also:

1. applic.)		$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Sinus CB. 5999549.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	gegen dem	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Radi. BA. 10000000.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	Also verhelt sich die bekante seit CB. 9. schuh gegen der gesuchten seiten BA. 15. schuh.
2.)	Wie sich verhelt		Tangens CB. 7499119.				Secante BA. 12499471.
3.)			Radius CB. 10000000.				Secante BA. 16667920.

Darnach die seite AC. also:

1.)	Wie sich verhelt	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Sinus BC. 5999549.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	gegen dem	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	Sinu CA. 8000338.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	Also verhelt sich die bekante seit BC. 9. schuh gegen der gesuchten CA. 12. schuh.
2.)			Tangens BC. 7499119.				Radio CA. 10000000.
3.)			Radius BC. 10000000.				Tangente CA. 13334900.

Allhie vnd im vorigen ist der dritte modus der beste vnd leichteste.

Die andere Regel.

Wann an einem winckelrechten triangel

neben der bekandten seiten die zwen spitzige winckel zwar nit bekandt / aber doch deren Proportion gegeneinander angezeigt würde: wie darauß jhr grösse / vnd dann auch die vbrigen seiten zuerkundigen.

In vorigem Exempel wann die zwen spitzwinckel A. vnd B. zwar nit bekandt / aber doch angezeigt würde das sie in solcher Proportion / wie die zwo zahlen 553. vnd 797. gegen einander stehen / wirdt nach der Regel von Gesellschafften (deren fundament steht in der 18. Proposition deß 5. Buchs Euclidis) also procedirt.

Addier die zwo proportionirte zahlen. Die Summ 1350. setze anfangs in die Regel Detri. In die mitten aber gehören allezeit 90°. (dann so viel thun die zwen spitzige winckel in einem rectangulo, wie droben am 20. blat gelehrt worden.) Zu letzten setz vnterschiedlich gemelte zahlen 553. vnd 797. so kommmen für den winckel A. 36°.52′. vnd für B. 53°.8′.

A. 553.
B. 797.
1350.	––90°.–––	$\left\{{\begin{aligned}\\\end{aligned}}\right.$	533. 797.	facit	$\left\{{\begin{aligned}\\\end{aligned}}\right.$	56°.52′. A. 53°.08′. B.

Wann nun die winckel erkundiget / wirdt mit erforschung der vbrigen zweyen seiten gehandelt allermassen wie in voriger Regel gelehrt.

Die dritte Regel.

Wann an einem winckelrechten triangel

die zwo seiten bekandt / wie man darauß die dritt vnbekandte / zu sambt beeden Spitzigen winckeln erfahren soll.

Diese Regel hat zwen Casus. Dann vnter den zwo bekandten seiten entweder nur eine / oder aber alle beyde den rechten winckel einfassen.

Vom ersten Casu.

In dem triangulo ABC. sollen die zwo bekandte seiten sein / die hypotenusa AB. 15. vnd cathetus BC. 9. schuh / den rechten winckel C. fassent. Auß diesen datis werden die zwen Spitzwinckel A. vnd B. gesucht / entweder nach dieser figur / also:

Wie sich verhelt AB. 15. schuh gegen BC. 9. schuh: Also verhelt sich der Radius AB. 10000000. gegen dem Sinu BC. 6000000. Welchen Sinum so man nach der 5. Regel deß Andern Theils in den Taflen sucht / gibt er beynahe den arcum 36°.52′. welches ist die grösse deß gesuchten winckels A. vnd gleich gegen vber zur rechten findet man sein complement 53°.8′. welches ist der ander winckel B.

(NB. Wann man vorhabenden Sinum 6000000. nach der 5. Regel deß Andern Theils genawer suchen solte / wirdt er geben 36°.52′.11″. vnd also sein complementum 53°.7′.49″. Aber zu vermeidung weitläuffigkeit wirdt solches vmbgangen / welches auch in volgenden Exemplen geschehen.)

Oder nach dieser figur also: Wie sich verhelt CB. 9. gegen BA. 15. also helt sich der Radius CB. 10000000. gegen deß winkels B. seiner Secante BA. 16666666. welche in der Taflen gesucht / gibt beynahe den arcum 53°.8′: die grösse deß winckels B. vnd also gegenüber sein complement A. 36°.52′.

Deßgleichen / so die bekandte zwo seiten weren hypotenusa AB. 15. vnd basis AC. 12. procedirt man nach dieser figur aso: Wie sich verhalt BA. 15. gegen AC. 12. also verhaltet sich Radi. BA. 10000000. gegen deß winckels B. seinem Sinu AC. 8000000. welcher in den Taflen gibt 53°.8′. die grösse deß winckels B. vnnd also sein complement A. 36°.52′.

Oder aber nach dieser figur also: Wie sich haltet CA. 12. gegen AB. 15. Also haltet sich der Radius CA. 10000000. gegen deß winckels A. seiner Secante AB. 12500000. Welche Secans in den Taflen gibt beynahe 36°.52′. die grösse deß gesuchten winckels A. vnd gleich gegenüber sein complement B. 53°.8′.

Vom anderen Casu.

Die bekandten seiten / beede den rechten winckel einschliessende / seind AC. 12. vnd CB. 9. schuh. Darauß werden die zwen spitzwinckel A. vnd B. gesucht / widerumb auff zweyerley weiß.

1. (Besihe die dritte figur am vorhergehenden 30. blat:) Wie sich helt AC. 12. gegen CB. 9. So helt sich Radius AC. 10000000. gegen der Tangente CB. 7500000. die gibt in den Taflen 36°.52′. als den winckel A. vnd^[12] sein complementum B. 53°.8′.

2. (Besihe die erste figur am vorhergehenden 30. blat:) Wie sich helt BC. 9. gegen CA. 12. Also Radius BC. 10000000. gegen der Tangente CA. 13333333. die gibt in Taflen den winckel B. 53°.8′. vnd sein complement A. 36°.52′.

So nun in einem vnd anderm Casu die zwen spitzige winckel also gefunden worden / kan man darnach auch leichtlich die dritte vnbekandte seit suchen / nach der Lehr der 1. Regel.

Hierbey zumercken / das gemeldte dritte vnbekandte seit auch ohne vorhergehende wissenschafft der zwen spitzwinckel kan gesucht werden / durch die 47. Proposition deß 1. Buchs Euclidis. Als wann AB. vnbekandt were / so addirt man das quadrat von AC. 12. vnd CB. 9. nemblich 144. vnd 81. Summa 225. dessen radix 15. ist die seit AB. Item so BC. vnbekandt / so subtrahiert man 144. das quadrat der seiten AC. von 225. dem quadrat der seiten AB. bleibt das quadrat 81. dessen radix 9. ist die gesuchte seit BC. Also / wann AC. vnbekandt / subtrahier 81. von 225. bleiben 144. dessen radix AC. 12.

Die vierdte Regel.

Wann in einem winckelrechten triangel

nicht zwo / wie in voriger Regel / sondern nur ein seiten bekandt were / vnd doch die proportion angezeigt würde / so zwo seiten desselben triangels / (sie seyen welche sie wollen) gegen einanderhaben / wie darauß nit allein die zwo vnbekandten seiten / sondern auch die zwen Spitzwinckel zuerfahren.

In vorigem triangel ABC. sey die einig bekandte seit BC. 9. schuh. Darneben werde angezeigt / das BC. vnd CA. in proportione subsequitertia, das ist / wie 3. vnd 4. gegen einander stehn. Dieser zweyen zahlen 3. vnd 4. jhre quadrat 9. vnd 16. addirt / machen das quadrat 25. dessen radix 5. ist die seite AB. den zwo gegebenen Proportional zahlen 3. vnd 4. respondierent. Damit man aber die zwo vnbekandte seiten AB. vnd CA. auch in solchen theilen / deren die bekandte BC. 9. hat / nemblich in schuhen haben möge / wirdt also concludirt:

Wie sich verhalten 3. als die Propor- tional zal der seiten BC. gegen	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	4. der Proportional zahl der seiten CA.	$\left.{\begin{aligned}\\\\\\\\\end{aligned}}\right\}$	Also verhelt sich auch die bekandte seit BC. 9. schuh gegen	$\left\{{\begin{aligned}\\\\\\\\\end{aligned}}\right.$	CA. 12. schuh.
		5. der Proportional zahl der seiten BA.				BA. 15. schuh.

So nun die seiten bekandt / werden volgents auch die winckel durch vorige 3. Regel leichtlich gesucht. Wiewol dergleichen auffgaben auch durch andere weiß zu solvirn / so die vbung an die hand gibt / vnd hie ohn not alles zumelden.

Bißher von den Rectangulis oder winckelrechten triangeln. Volgen die Obliquangula, schlimm wincklichte / so eintweder alle drey winckel scharff / oder einen darunter stumpff haben.

Die fünffte Regel.

So in einem Obliquangulo die zwen

winckel (vnd also auch der dritte / als jener zweyen Complement zu 180°.) zu sampt einer seiten bekandt / wie darauß die zwo andern vnbekanten seiten zu finden.

Die seiten eines jeden Triangels stehn in der Proportion gegen einander / wie die Sinus der gegen jhnen vberstehenden winckel. Wann nun die winckel bekandt / weiß man auch der seiten Proportion: Vnd also wann ein seite in einer gewissen maß bekandt / wirdt auch die grösse der andern zweyen / eben in dergleichen maß / durch die Regel Detri erkündiget / wie auß volgendem Exempel leichter zuvernehmen.

In diesem scharffeckenden Triangel seye bekandt erstlich die seit AB. 10. schuh. darnach der winckel A. 60°. vnd B. 84°. vnd also auch beeder complement C. 36°. dieser dreyen winckel jhre sinus schreibe man zu jhren subtensis oder vnterzogenen seiten: als den sinum deß winckels A. 8660254. zur seiten BC. den sinum B. 9945219. zu AC. Item den sinum C. 5877852. zu AB. so hat man der dreyen seiten proportion in dergleichen theilen / deren 10000000. der radius hat. Wil man nun ferner die zwo vnbekandten seiten AC. vnd BC. in der maß / so die gegebene seit AC. hat / nemblich in schuhen bekandt machen / so setze man in der Regel Detri anfangs den Sinum deß winckels C. deme die bekandte seit AB. vnterzogen ist: in die mitte wirdt gemelte seit AB. 10. schuh / vnd zu letzt die sinus der andern zwen winckel gesetzt vnd also geschlossen:

Deß winckels C. 36°. sinus 5877852. gibt gegen vber die seit AB. 10. schuh.

Derhalben /

Deß winckels B. 84°. sinus 9945219	$\left.{\begin{aligned}\\\\\\\end{aligned}}\right\}$	wirdt geben die ge- genüberstehende seiten	$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$	AC. 17. schuh.
Des winckels A. 60°. sinus 8660254.				BC. 15. schuh.

Wann der Triangel stumpffeckent ist / weil ein stumpff vnd scharffer winckel einerley sinum haben / wie droben zu anfang deß andern theils gemeldet worden / so subtrahirt man den stumpffen winckel von 180°. vnd nimbt deß rests sinum, vnd procedirt allermassen wie jetzt gelehrt.

Als in beystehender figur so der winckel B. 108°.2′. von 180°. abgezogen wirdt / gibt der rest oder complement 71°.58′. den sinum 9508766. So nun die seit BC. 9. schuh bekandt / werden die andern zwo BA. vnnd AC. gesucht / wie droben / nemblich also:

Wie sich halten 6582516. sinus deß winckels A. 41°.10′. zu der bekandten seit BC. 9. schuh.

Also halten sich	$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$	9508766. sinus deß winckels B. 71°.58′.	$\left.{\begin{aligned}\\\\\\\end{aligned}}\right\}$	zu der seite	$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$	AC. 13. schuh.
		5120429. sinus deß winckels C. 30°.48′.				AB. 7. schuh.

Die Exempel dieser Regel mögen auch / wiewol mit mehrer weitleuffigkeit / durch die erste Regel solvirt werden: doch das man vorher von einem spitzen deß Triangels ein Perpendicular oder wagrechte lini auff die vnbekandte seiten herab fallen lasse.

Als das erstgehabte Exempel wirdt nach dieser figur also solvirt. Die bekandte seit ist AB. 7. schuh. die bekandte winckel seint A. 41°.10′. B. 108°.2′. C. 30°.48′. die Perpendicular auff die vnbekante seite AC. gesenckt / ist BD. darauß wird nach der ersten Regel erstlichen die vnbekandte seit BC. also gesucht / durch diese zwo analogias.

1. Wie sich in dem Triangel ABD. verhelt AB. radius 10000000. gegen deß winckels A. 41°.10′. seinem sinu BD. 6582516. Also verhelt sich die bekandte seit AB. 7. schuh / gegen der perpendicular BD. $4{\tfrac {3}{5}}.$ schuh.

2. Ferner in dem Triangel DBC. wie sich verhelt der radius DB. 10000000. gegen BC. 19529615. als der secante deß winckels DBC. 59°.12′. (NB. Diesen winckel erfehrt man / so man C. 30°.48′. vom Quadranten subtrahirt: dann er deß winckels C. conplement ist) Also verhelt sich auch die Perpendicular DB. $4{\tfrac {3}{5}}.$ schuh / gegen der gesuchten seit BC. 9. schuch ferè.

Zum andern wirdt ebenmeßig durch zwo analogias die andere vnbekandte seit AC. gesucht. Dann es wirdt von dem spitzen A. die Perpendicular AE. auch auff die vnbekandte lini BC. (die doch vorher gnugsam erlengert werden muß) gesenckt: vnd darnach also geschlossen.

1. Wie sich in dem Triangel ABE. verhelt Radius AB. 10000000. gegen AE. 9508766. als dem Sinu deß winckels ABE. 71°.58′. (welcher winckel gefunden wirdt / so man den bekandten winckel ABC. 108°.2′. abziehet vom semicirculo 180°. weil er dessen complement ist) Also verhelt sich auch die bekandte seit BA. 7. schuh gegen der Perpendicular AE. $6{\tfrac {13}{20}}.$ schuh.

2. Ferner in dem Triangel AED. wie sich verhelt radius EA. 10000000. gegen AC. 19529615. als der Secante deß winckels EAC. 57°.12′. (NB. Dieser winckel wird also erfahren. Man addirt den gegebenen winckel CAB. 41°.10′. zu dem winckel BAE. 18°.2′. Als der deß obgemelten winckels ABE. complement zum quadranten ist / Summa 59°.12′.) Also verhelt sich die vorher gefundene Perpendicular EA. $6{\tfrac {13}{20}}.$ gegen der gesuchten seiten AC. 13. ferè.

Die sechste Regel.

So die drey winckel nicht / aber doch jhr

Proportion gegen einander anzeigt würde / wie darauß jhr grösse / vnd volgends auch / so ein seit bekandt / die vbrigen seiten zuerkündigen seyen.

Die Proportion der winckel wirdt gegeben in zahlen / so eintweder continuè, oder aber discretè, proportional seint.

Vom ersten Casu.

Seint sie continuè proportional / so geschicht die operation nach der 18. proposition deß 5. buchs Euclidis / wie droben in der andern Regel gelehrt.

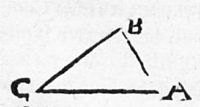
Als die 3. winckel dieses Triangels stehn gegen einander wie 5. 7. 3. also das A. gegen B. ist / wie 5. gegen 7. vnd B. gegen C. wie 7. gegen 3. werden derhalben die winckel gesucht / wie droben gelehrt / also:

5
7
3	0	$-\left\{{\begin{aligned}\\\\\end{aligned}}\right.$	5	— A 60°.
15	–180		7	— B 84°.
1.	12.		3	— C 36°.

Vom andern Casu.

So sie aber discretè proportional seint / werden sie zu continuè proportional zahlen gemacht durch die 4. Proposition deß 8. buchs Euclidis. Als wann in vorigem Triangel gesagt würde / der winckel A. halt sich gegen B. wie $1{\tfrac {3}{7}}.$ gegen 2. Item B. gegen C. wie 7. gegen 3. hat man vier discretè Proportional zahlen / $1{\tfrac {3}{7}}.$ 2. 7. 3. die werden zu drey continuè proportional zahlen also gemacht / das man multipliciere die erst mit der dritten / die andere mit der dritten / vnd die andere mit der vierten: kommen 10. 14. 6. oder (so man sie durch den gemeinen Theiler 2. in kleinere zahlen bringen will) 5. 7. 3. wie allhie zusehen

	A. $1{\tfrac {3}{7}}.$		B. 2.		B. 7.		C. 3.
		10.		14.		6.
2)		5. A.		7. B.		3. C.

Weil man nun die winckel in continuè proportional zahlen hat / wirdt jhr grösse allerdings wie im ersten Casu, vnd dann die vbrigen zwo seiten nach vorgehender Regel gesucht.

Die sibende Regel.

So in einem Obliquangulo angeben

würden erstlich zwo seiten / darnach ein winckel / so der einen auß gemelten zwo seiten entgegen gesetzt würde: wie man darauß die andern winckel / vnd dritte seit erkündigen solle.

Diese Regel gründet sich auch auff das theorema, so droben in der fünfften Regel anfangs gemeldet worden: das nemblich in einem jeden Triangel die seiten eben in der Proportion gegen einander stehen / wie die Sinus jhrer gegenvberstehenden wincklen. Derhalben setzet man in die Regel Detri anfangs die jenig bekandte seit / so dem bekandten winckel vnterzogen: in die mitte aber den sinum deß bekandten winckels / vnd zu letzt die andere bekandte seit: so kombt herauß der sinus deß winckels / so der gemelten anderen bekandten seit entgegen steht: welcher zum vorigen bekandten winckel addirt / vnd die Summ von 180°. subtrahirt / gibt den dritten winckel. So nun die winckel alle bekandt / wirdt nach der fünfften Regel die dritte seit auch leichtlich gefunden.

Es begeben sich aber allhie zwen Casus. Dann der bekandte vnd gegebene winckel ist entweder Obtusus stumpff / oder acutus scharff.

Vom ersten Casu.

In diesem Triangel ABC. seye bekandt erstlich die seit AB. 7. schuh / darnach die seit AC. 13. vnd dann der stumpffe winckel ABC. 108°.2′. Auß diesen dreyen datis seint die vnbekandten zwen winckel A.C. vnd die seit BC. zuerkundigen solcher gestalt:

Wie sich verhelt AC. 13. schuh gegen 9508766 (als dem sinu deß gegenvberstehenden winckels B. 108°.2′. das ist / seines complementi 71°.58′.) also verhelt sich auch die seit AB. 7. schuh gegen 5120104. dem sinu deß gegen vberstehenden winckels C. welcher sinus in den Taflen gesucht / weiset die grösse deß winckels C. nemblich 30°.48′. So nun C. 30°.48′. zu B. 108°.2′. addirt / vnd die Summa 138°.50′. von 180°. abgezogen wirdt / bleibt der winckel A. 41°.10′.

Es können aber diese winckel auch mit hilff der ersten vnd dritten Regel / zwar müh- vnd langsamer als durch vorhabende Regel / gefunden werden: doch das man vorher von einem der vnbekandten wincklen ein perpendicular auff die vnterzogene seit fallen lasse.

Als im vorigem Exempel sollen vorgemelte data bleiben / vnd die Perpendicular AE. gezogen werden. Weil nun der winckel ABC. 108°.2′. bekandt / so kan man auch seiin complement ABE. 71°.58′. wissen / vnd darauß die grösse der Perpendicular AE. nach der ersten Regel solcher gestalt erfahren:

Wie sich helt radius BA. 10000000. gegen AE. 9508766. (als dem sinu deß jetzgemelten winckels ABE. 71°.58′.) Also helt sich die seit BA. 7. schuh gegen der Perpendicular AE. $6{\tfrac {656}{1000}}$ schuh.

Ferners nach der dritten Regel schliesset man also: Wie sich verhelt CA. 13. schuh gegen AE. $6{\tfrac {656}{1000}}.$ schuh: Also verhelt sich radius CA. 10000000. gegen dem sinu AE. 5120000. welcher in Taflen gesucht / gibt den winckel C. 30°.48′. wie vor / vnd also auch A. 42°.10′.

So nun die winckel also nach einem oder dem andern weg gefunden / so kan darauff auch die noch vnbekandte seit BC. durch die fünffte Regel also erfahren werden: Wie sich verhelt 5120429. der sinus deß winckels C. 30°.48′. gegen der jhm vntergezogenen seiten AB. 7. schuh (oder aber / wie sich verhelt 9508766. sinus deß winckels B. 108°.2′. gegen der seite AC. 13. schuh.) Also verhelt sich auch 6582516. der sinus deß winckels A. 41°.10′. gegen der seite BC. 9. schuh.

Vom anderen Casu.

Im fall aber der gegebene winckel scharff were / muß angezeigt / oder aber auß fleißigem abriß deß Triangels gesehen werden / ob einer auß den vnbekandten wincklen stumpff oder nicht sey. Dann wann der jenige winckel / so man erstlich suche will / auch spitzig ist / wirdt allerdings procedirt / wie droben im ersten Casu: so er aber stumpff were / wann man im operirn seinen sinum findet / muß man nicht nemen denselben arcum, so solcher sinus in den Taflen hat / sondern dessen complement / wie auß volgendem Exempel klärlicher zuverstehn.

In vorigem Triangel ABC. (besih die figur am 40. blat) seyen bekandt erstlich die seit AB. 7. schuh / darnach AC. 13. schuh / vnd dann der scharff winckel C. 30°.48′. Auß diesen dreyen datis werden die andern zwen winckel vnd die seit BC. also erkündigt.

Wie sich verhelt AB. 7. schuh gegen 5120429. als dem sinu deß gegenvberstehenden winckels C. 30°.48′. Also verhelt sich die seit AC. 13. schuh / zu deß gegenvberstehenden winckels ABC. seinem sinu 9509368. welcher in den Taflen gesucht / gibt den arcum 71°.58′. weil aber der gesuchte winckel stumpff ist / muß man solchen arcum von 180°. abziehen / bleibt sein complementum 108°.2′. welches ist die eigentliche grösse deß gedachten winckels B. die zu C. 30°.48′. addirt / vnd die Summa 138°.50′. von 180°. subtrahirt / gibt den winckel A. 41°.10′. Darauß wirdt die seit BC. gesucht / wie droben zu ende deß ersten Casus vermeldet.

Vnd diß ist zwar der richtigste weg. Wo aber jemand beliebte weiter herumb zuschweiffen / der procediere also. Kurtzvorgemelte data in dem Triangel ABC. welchs am 40. blat zu sehen) sollen bleiben / vnd die Perpendicular AE. gezogen werden: dardurch dann zwey rectangula, nemblich ACB. vnd ABE. gemacht werden.

1. Vnd ist erstlich die grösse der Perpendicular AE. wie auch der lini CE. durch die erste Regel also zu suchen: In dem rectangulo AEC. weiß man erstlich den gegebenen winckel C. 30°.48′. vnd also sein complement CAE. 59°.12′. derhalben wie sich helt radius CA. 10000000. gegen AE. 5120429. dem sinu deß winckels C. Also die bekandte seit CA. 13. schuh gegen der Perpendicular AE. $6{\tfrac {656}{1000}}.$ Darnach eben im selben rectangulo wie sich helt radius AE. 10000000. gegen EC. 1677556. (als der Tangente deß winckels EAC. 59°.12′.) Also verhelt sich die Perpendicularis AE. $6{\tfrac {656}{1000}}.$ gegen der lini EC. $11{\tfrac {16}{100}}.$ schuh.

2. Ferner / weil in andern rectangulo AEB. die zwo seiten AB. 7. schuh / vnd AE. $6{\tfrac {656}{1000}}.$ schuh bekandt / wirdt darauß durch die dritte Regel der winckel ABE. also gesucht / wie sich verhalt BA. 7. schuh gegen AE. $6{\tfrac {656}{1000}}.$ schuh / also helt sich radius BA. 10000000. gegen dem sinu AE. 9508571. welcher in den Taflen gesucht / gibt den winckel ABE. 71°.58′. dessen complement ist der gesuchte stumpff winckel ABC. 108°.2′. welcher zu dem gegebenen winckel C. 30°.48′. addirt / vnd die Summa 138°.50′. vom semicirculo 180°. subtrahirt / gibt den andern gesuchten winckel BAC. 41°.10′.

3. Zum dritten wirdt die lini BE. durch die erste Regel also gesucht: wie sich helt radius AE. 10000000. gegen BE. 3255630. als der Tangente deß winckels BAE. 18°.2′. (welcher ist das complement deß vorgefundenen winckels ABE. 71°.58′.) Also helt sich die Perpendicular AE. $6{\tfrac {656}{1000}}.$ der lini EB. $2{\tfrac {16}{100}}.$ welche / so sie von der vorgefundenen gantzen lini EC. $11{\tfrac {16}{100}}.$ abgezogen wirdt / bleibt die gesuchte dritte seit BC. 9. schuh.

Die achte Regel.

So im Triangel ein winckel / sambt

zweyen vngleichen seiten / die solchen winckel beschliessen / geben würde: wie darauß die andern zwen winckel vnd dritte seit zu erkundigen.

Dergleichen vorgaben müssen auff solche weiß solvirt werden:

1. Addire man die zwo bekandte seiten / vnd setze die Summ anfangs in die Regel Detri.

2. Neme man jhr differentz durch abziehung der kleinern von der grössern / solche differentz gehört in die mitte der Regel.

3. Der bekandte winckel werde vom semicirculo 180°. abgezogen / vnd der rest halbirt / auch solchen halben theils sein Tangens genommen / vnd in die Regel Detri zu ende gesetzt: So wird herauß kommen ein Tangens, welche anzeiget einen gewissen arcum, der zu vorgemelter halber Summ der zweyen winckel addirt / gibt den grössern: aber subtrahirt / den kleinern der zweyen gesuchten winckel / wie solches auß beygefügtem Exempel leichter zuverstehn.

In diesem Triangel ABC. seye bekandt der winckel A. 41°.10′. vnd die zwo jhn beschliessende seiten AB. 7. schuh / vnd AC. 13. schuh. Auß welchen datis die vbrigen zwen winckel B. C. vnd die seite BC. also erfahren werden.

1. Die Summa der gegebenen seiten AB. 7. vnd AC. 13. ist 20.

2. Darnach so man die kleiner 7. von der grössern 13. subtrahirt / bleibt jhr differentz 6.

3. Ferner durch abziehung deß winckels A. 41°.10′. von 180°. bleiben 138°.50′. welche ist die Summa der winckel / B. vnd C. deren halb theil ist 69°.25′. welchem halben theil gebürt die Tangens 26628085. darauß schliesse also: Wie sich verhelt die Summa der gegebenen seiten 20. zu dero differentz 6. Also verhelt sich 26628085. die Tangens der halben Summ der zweyen vnbekandten winckel / gegen der Tangente 7988425. die gibt in den Taflen den arcum 38°.37′. welcher arcus so er zu obgemeltem halbentheil 69°.25′. addirt wirdt / kombt der grösser gesuchte winckel B. 108°.2′. so er aber davon wirdt subtrahirt / kombt der kleinere winckel C. 30°.48′.

Entlich die seit BC. wirdt nach der fünfften Regel also gesucht: wie sich helt deß winckels C. sinus 5120429. gegen AB. 7. schuh / also helt sich der sinus deß winckels A. 6582516. gegen BC. 9. schuh.

Vnnd diß ist die richtigste operation: die zwar auch durch die erste vnd dritte Regel / aber etwas weitleuffiger / verrichtet wirdt / wie auß beygesetztem Exempel zuvernemen.

In dem Triangel ABC. seye bekandt der winckel C. 30°.48′. sambt beeden seiten / so jhn beschliessen CB. 9. schuh / vnnd CA. 13. schuh. Darauß die dritte seit vnd zwen winckel zuerfahren / ziehe man die Perpendicular AE. gegen dem bekandten winckel C. vber / vnd suche allerdings / wie droben gegen dem ende der sibenden Regel geschehen / die Perpendicular AE. $6{\tfrac {656}{1000}}.$ schuh / vnd die seit CE. $11{\tfrac {167}{1000}}.$ davon subtrahir die bekandt seit CB. 9. schuh / bleibt BE. $2{\tfrac {167}{1000}}.$ Auß diesen schliesset man also: Wie sich halt BE. $2{\tfrac {167}{1000}}.$ gegen EA. $6{\tfrac {656}{1000}}.$ also BE. radius 10000000. gegen der

Tangente EA. 30715274. welche Tangens in Taflen gesucht / gibt den winckel ABE. 71°.58′. dessen complement ist der gesuchte winckel ABC. 108°.2′. welcher zu dem gegebnen winckel C. 30°.48′. addirt / vnd die Summ 138°.50′. von 180°. subtrahirt / gibt den dritten winckel CAB. 41°.10′. Entlich die dritte seit AB. wirdt also gesucht: Wie sich helt radius EB. 10000000. gegen BA. 32302846. (der secante deß winckels ABE. 71°.58′.) also helt sich EB. $2{\tfrac {167}{1000}}.$ schuh gegen der seite BA. 7. schuh.

Zu mercken / das derentwegen im Titel dieser Regel gemeldet worden / es müssen die zwo den bekandten winckel einschliessende seiten vngleich sein / dieweil nach der fünfften Proposition deß ersten Buchs Euclidis / in einem Isoscele, oder aequicruro, (das ist / in einem Triangel von gleichen schencklen) die zwen winckel bey der basi oder grundlini einander gantz gleich / vnd also gesucht werden: den gegebnen winckel / als allhie den winckel A. 45°. subtrahier von 180°. bleiben 135°. dessen halber theil 67°.30′. ist die grösse so wol deß winckels B. als C. So nun auch die seit AB. oder AC. bekandt / als / zum Exempel / von 10. schuhen were: erkundiget man die dritte seit BC. nach der fünfften Regel also: wie sich helt deß winckels B. sinus 9238795. gegen AC. 10. schuh: Also helt sich deß winckels A. sinus 7071068. gegen der seite BC. $7{\tfrac {15}{23}}.$ schuh.

Die neundte Regel.

So in einem Triangel alle drey seiten

angeben werden / wie darauß die drey winckel desselben zueröffnen.

Es hat diese Regel drey Casus, nach der dreyfachen art der Triangel. Dann ein jedes Triangel ist eintweder aequilaterum, gleichseitig: oder Isosceles, gleichfüssig / von gleichen schencklen: oder scalenum, vngleichseitig.

Vom ersten Casu.

Ist das vorgebene Triangulum / aequilaterum vnnd von gleichen seiten / so seint auch die drey winckel einander gleich / nach dem corollario der fünfften Proposition deß ersten Buchs Euclidis. Vnd weil sie alle drey samentlich so viel vermögen / als zwen rechte winckel oder 180°. nach der 32. Proposition deß ersten Buchs Euclidis / so wirdt ein jeder derselben insonderheit ${\tfrac {1}{3}}.$ von 180°. das ist 60°. vermögen.

Vom anderen Casu.

Ist aber das Triangulum Isosceles, vnnd von zwen gleichen schencklen / so wirdt die basis oder grundlini durch ein Perpendicular vom obstehenden spitzen herab in zwen gleiche theil getheilet: vnnd als dann durch die dritte Regel die winckel gesucht. Als in dem Isoscele

ABC. sollen die zwen gleichen schenckel AB. vnd AC. jeder 10. schuh / vnd die basis BC. 6. schuh halten. So nun vom spitzen A. auff die basin BC. die Perpendicular AD. fellt / theilet sie die selb in zwen gleiche theil BD. vnd DC. jedes 3. schuh. Weil nun in dem winckelrechten Triangel ABD. zwo seiten bekandt / nemblich AB. 10. vnnd BD. 3. schuh / werden die winckel also gesucht: Wie sich verhelt die seit AB. 10. schuh gegen BD. 3. schuh / also verhelt sich radius AB. 10000000. gegen dem sinu BD. 3000000. welcher in den Taflen gibt den winckel BAD. 17°.28′. dessen complement ist der winckel B. 72°.32′. vnd so groß ist auch C. Gedachte 17°.28′. geduplirt / geben den gantzen winckel A. 34°.56′.

Vom dritten Casu.

Die Scalena, da alle drey bekandte seiten vngleich / werden gleichfals / wie im anderen Casu geschehen / durch ein Perpendicular (so von dem grösten winckel auff die gröste seit muß gesenckt werden) in zwey rectangula getheilt: jedoch weil solches in basi vngleiche theil gibt / muß zuvor derselben grösse auff solche weiß erfahren werden.

1. Die gröste seit setze anfangs in die Regel Detri.

2. Die andern zwo seiten / so den grösten winckel beschliessen / addire / vnd setze die Summ in die mitte.

3. Eben derselben zwo seiten jhr differentz (die man durch abzug der kleinern von der grössern erfehrt) setz zu ende: kombt durch die operation ein segmentum oder stuck / welches so es von der grösten lini / als von der basi oder grundlini abgezogen wirdt / so fellet die perpendicular in die mitte deß noch vberbleibenden Segments.

Zum Exempel / in dem Scaleno ABC. seye die seit BC. 21. schuh / BA. 20. vnd AC. 13. vnd werde von dem grösten winckel A. auff die gröste seit BC. die Perpendicular AD. gesenckt / die macht zwey segmenta, BD. vnd DC. deren grösse also zusuchen. Wie sich verhelt die gröste seit BC. 21. schuh gegen 33. (als der Summa der andern zweyen seiten BA. 20. vnd AC. 13.) also verhelt sich 7. (die differentz gedachter beeder seiten) gegen dem Segment BE. 11. schuh / welches so es von der gantzen lini BC. 21. schuh abgezogen wirdt / bleibt das Segment EC. 10. schuh / in dessen mitte D. die Perpendicular AD. fellet. Helt also das kleiner Segment CD. 5. schuh / vnd das grössere DB. 16. schuh.

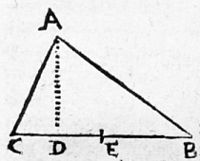
Darauß dann ferner nach anleitung der dritten Regel die winckel also gesucht werden. Erstlich in dem rectangulo ADB. Wie sich helt das Segment DB. 16. schuh gegen der seit BA. 20. schuh. Also helt sich radius DB. 10000000. gegen der secante BA. 1250000. welche in den Taflen gibt den winckel B. 36°.53′.

Darnach in dem rectangulo ADC. Wie sich helt das Segment DC. gegen der seiten CA. 13. Also helt sich der radius DC. 10000000. gegen der secante CA. 26000000. welche in den Taflen gibt den winckel C. 67°.23′. welchen so man zu dem winckel B. 36°.53′. addirt / vnd die Summ 104°.16′. von 180°. subtrahirt / bleibt der winckel BAC. 75°.44′.

Im fall aber die seiten an jhnen selbst nicht / sondern nur ein gewisse gegen einander tragende proportion derselben angeben / vnd die winckel darauß zuerkundigen begert würde / so werden dieselben proportional zahlen (doch so fern sie continuè proportional. So sie aber discretè proportionirt / müssen sie vorher nach der lehr der obgesetzten 6. Regel in continuè proportional zahlen verwandlet werden) an statt der seiten selbst genommen / vnd damit nach anleitung vorhabender Regel gehandlet: Inmassen auß volgendem Exempel abzunehmen.

In vorigem Triangel ABC. sollen die seiten nicht selbst / sondern nur jhr proportion geben: vnd angezeigt werden / das AB. gegen AC. sich halte wie 60. gegen 39. vnd AC. gegen BC. wie 39. gegen 63. Diese drey continuè proportional zahlen 60. 39. 63. werden an statt der seiten genommen / vnd die gröste darunter / nemblich BC. 63. anfangs in die Regel Detri gesetzt. In die mitten gehören 99. als die Summa der andern beyden AB. 60. vnd AC. 39. zu letzt setze man 21. die differentz erstgemelter zwo seiten (dann so viel bleiben / so 39. von 60. abgezogen werden.) Nach vollendter operation kombt das facit 33. welches ist das segment BE. das / so es von der gantzen lini BC. 63. abgezogen

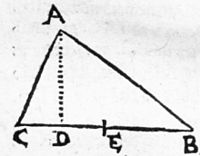
wirdt / bleibt das segment EC. 30. in dessen mittel D. die Perpendicular AD. fellet / vnd also zwey segmenta macht / nemblich BD. 48. DC. 15. vnd vorhabendes Triangel / in zwey rectangula theilet / darauß die winckel / wie droben / also gesucht werden:

In ABD. wie sich helt DB. 48. gegen BA. 60. Also radius DB. 10000000. zur secante 12500000. 36°.53′. B.

Item in ADC. wie sich helt DC. 15. gegen CA. 39. Also radius DC. 10000000. zur secante 26000000. 67°.23′. C.

Welche zwen gefundene winckel 36°.53′. B. vnd 67°.23′. C. addier: die Summ 104°.16′. subtrahier von 180°. rest der dritte winckel A. 75°.44′.

Deßgleichen so gemelte seiten in discretè proportional zahlen angeben / vnd zum Exempel / gemeldet würde / es halte sich AB. gegen AC. wie 60. zu 39. vnd AC. gegen BC. wie 26. zu 42. so werden solche vier termini zu dreyen continuè proportional zahlen auff solche weiß gemacht:

	AB. 60.		AC. 39.		AC. 26.		CB. 42.
		1560.		1014.		1638.[13]
26)		60. AB.		39. AC.		63. CB.

Mit diesen gefundenen dreyen proportional zahlen der seiten / werden die drey winckel gesucht allerdings wie kurtz zuvor.

Soviel seye genug von nachvolgenden tabulis sinuum, vnd wie darauß alle rectilinea triangula zu solvirn / bericht: darauß hoffentlichen einer / so auch der Lateinischen Sprach vnerfahren (doch das er zuvor die Lateinische hierinn gebrauchte terminos auß dem ersten theil dieses Tractats wol verstehn lerne) ohn fernere anleitung leichtlich fortkommen mag.

Wann es das Format dieses Handbüchlins hette leiden mögen / were auch von der praxi vnd gebrauch dieser lehr in Mathematica, vnd derselben anhangenden Künsten gehandlet worden / solle aber doch zur andern gelegenheit den Kunstliebenden zu gutem / bevorab so vermerckt würdt / das jhnen solch mein geringfügig arbeit nicht vnangenehm / dieses in einem sondern Tractat beschehen.

Damit aber doch der günstige Leser hievon auch in diesem Tractätlein etwas habe / wollen wir allhie zu einem praegustu nur zwey Exempel einführen / eines zur Architectura militari, das ander zur Altimetria gehörig.

Fürs erste / soll man die eigentliche leng der Principal- vnd Hauptlinien in beygefügtem grundriß / der zwey halben Beluarden^[14] auß vorgegebenem bericht vnd tabulis sinuum erfahren. Ehe man aber zu solcher außrechnung schreitet / ist vonnöten / das man vorher alle winckel / die in solchem grundriß vorfallen / erkündige: welches volgender gestalt beschicht. Hiebeygesetzte zwey halbe Beluarden ACK. seint ${\tfrac {1}{8}}.$ eines achtecks. Derhalben helt A. der winckel im centro 45°. Dann dieses ist der Quotient / so die gantz circumferentz 360°. mit 8. dividirt wirdt. Wann

nun diese 45° . von dem Semicirculo, das ist / von 180°. abgezogen werden / so bleiben 135°. für den winckel in der circumferentz / dessen halber theil 67°.30′. ist der winckel ABE. diesen von 180°. als von zweyen rechten wincklen abgezogen / bleibt sein complement EBC. 112°.30′. Der winckel deß Beluard oder Bollwercks Spitz ist 90°. vnd also für den winckel deß halben Beluards DCB. 45°. So nun in dem Triangel CGB. die erst gemelte zwen winckel 45°. vnd 112°.30′. addirt / geben sie 157°.30′. solche von 180°. als zwen rechten wincklen abgezogen / bleibt jhr Complement zum semicirculo, nemblich CGB. oder DGE. 22°.30′. Dieses winckels complement zum Quadranten / ist GDE. 67°.30′. dessen complement zum halben circkel 180°. gibt den inwendigen winckel EDG. 112°.30′. Vnd weil ML. vnd DE. parallel linien seint / so ist der winckel MFD. dem alterno FDE. gleich (durch die 29. Prop: deß ersten Buchs Euclidis) vnd also auch von 62°.30′. Solchen duplir / so kombt NFD. 135°. so angulus flancans der streichwinckel / oder tenaille, das ist / die zang genennet wirdt.

Soviel nun fürs ander die dimension der linien betrifft / werden allhie für bekandt geben / erstlich die Cortin HE. 36. Ruten / (die Rut zu 12. schuhen gerechnet.) Darnach die spala oder achsel DE. 12. Ruten. Zum dritten der Beluarden gesicht DC. 24. Ruten. Auß welchen datis der winckel vnnd linien / die andern linien also bekandt gemacht werden.

Anfangs in dem Triangel DEG. wie sich helt radius DE. 10000000. gegen EG. 24142136. (welche ist Tangens deß winckels GDE. 67°.30′.) also verhelt sich die spala DE. 12. Rut. gegen EG. 29. Rut. die ziehe ab von der gantzen Cortin EH. 36. Rut: bleibt HG 7. Rut / auß welchen das gesicht deß Beluards gezogen wirdt.

Weiter in gemeltem Triangel wie sich halten radius ED. 10000000. gegen DG. 26131259. (welche ist secans deß winckels EGD. 67°.30′.) also halt sich die spala ED. 12. Rut / gegen GD. 31. Rut / 4. schuh / $3{\tfrac {1}{2}}.$ Zoll: (oder in brüchen / so wegen füglicher rechnung allhie zubehalten ${\tfrac {313575108}{10000000}}.$ Rut) darzu so man das gesicht deß Beluarden CD. 24. Ruten thut / so kombt die grösse der gantzen lini CG. 55. Rut. 4. schuh $3{\tfrac {1}{2}}.$ Zoll / (oder in gebrochenen zahlen / ${\tfrac {553575108}{10000000}}.$^[15] Rut.)

Ferner in dem Triangel BCG. wie sich deß winckels GBC. 112°.30′. sein Sinus 9238795. gegen der gegenüberstehenden seiten CG. 55. Rut. 4. schuh / $3{\tfrac {1}{2}}.$ Zoll (oder ${\tfrac {553575108}{10000000}}.$ Rut.) verhaltet / also auch verhaltet sich deß winckels CGB. 22°.30′. sein sinus 3826834. zu der auch gegenübergesetzten seit CB. 22. Rut. 11. schuh / $1{\tfrac {7}{9}}.$ Zoll / (oder ${\tfrac {229298305}{10000000}}.$ Rut.) welches ist die Hauptlini deß Beluards. Item eben im selben Triangel / wie sich haltet erstgemelter sinus 9238795. deß winckels GBC. zu der gegenüberstehenden seit CG. ${\tfrac {553575108}{10000000}}.$ Rut: Also deß winckels GCB. 45°. sinus 7071068. zu der auch entgegenstehenden seit GB. 42. Rut. 4. schuh / $5{\tfrac {1}{9}}.$ Zoll / (oder ${\tfrac {423688070}{10000000}}.$ Rut.) davon ziehe man ab die vorgefundene lini GE. 29. Rut / bleibt für die kehllini EB. 13. Rut. 4. schuh / $5{\tfrac {1}{9}}.$ Zoll. Zu dieser lini EB. addier die halb Cortin LE. 18. Rut. gibt 31. Rut. 4. schuh $5{\tfrac {1}{9}}.$ Zoll / welches ist die lini LB. die dupliere / kombt die gantze lini IB. 62. Rut. 8. schuh / $10{\tfrac {2}{9}}.$ Zoll.

Volgt jetzt das triangulum ABL. zu resolvirn, solcher gestalt: Wie sich helt radius LB. 10000000. gegen BA. 26131259. (welche ist secans deß winckels LBA. 67°.30′.) Also die vorgefundene seit LB. 31. Rut. 4. schuh / $5{\tfrac {1}{9}}.$ Zoll / (oder ${\tfrac {313688070}{10000000}}.$ Rut.) gegen BA. 81. Rut. 11. schuh / $7{\tfrac {4}{5}}.$ Zoll / (oder ${\tfrac {819706420}{10000000}}.$ Rut.) darzu addiere die droben gefundene BC. 22. Rut. 11. schuh / $1{\tfrac {7}{9}}.$ Zoll / erwechst die gantze AC. 104. Rut. 10. schuh / $9{\tfrac {5}{9}}.$ Zoll / (oder ${\tfrac {1049004725}{10000000}}.$ Rut.)

Ist also zu solvirn noch übrig der winckelrechte Triangel ACM. in welchem wie sich haltet radius AC. 10000000. gegen CM. 3826834. dem sinu deß winckels CAM. 22°.30′. also haltet sich die erstgesuchte seit AC. ${\tfrac {1049004725}{10000000}}.$ Rut / gegen CM. 40. Rut. 1. schuh / $7{\tfrac {7}{10}}.$ Zoll / welche duplier / so kombt KC. 80. Rut. 3. schuh / $3{\tfrac {2}{5}}.$ Zoll.

Wie nun alle linien deß halben Beluards beschaffen / einer ebenmeßigen grösse seind auch die andern: also das CD. vnnd NK. deßgleichen BC. vnnd IK. Item BE. vnd IH. etc. einander gantz gleich: Vnd wie diese / also auch die anderen wöhren / geordnet vnd angelegt werden müssen. Vnd ob wol viel vnterschiedliche meinungen / wie solche Hauptlinien zu ziehen / auff das sie zu notwendiger defension recht einander correspondirn / damit je ein wehr die andere defendiere: Jedoch wird ein jeder diß vnser Exempel mutatis mutandis leichtlich auff sein art zu fortificirn / zu richten wissen / vnd in warheit erfahrn / das solche außrechnung / so durch die tabulas Sinuum, vnd solution der Triangel beschicht / sehr genaw / vnd viel gewisser zutreffe / als wann man nur der gemeinen mechanischen art / die offt vmb viel Paurenschuch fehlt / sich gebrauchet: dardurch dann zu weilen grosser schad verursacht / vnd vnnützer Bawkosten angewendet würdt.

Hieneben zu mercken / das man in dergleichen rechnungen / in denen radius vornen in der Regel Detri / vnd also theiler ist / einen sondern vortel haben würde / so man an statt der Rut von 12. schuhen / ein decempedam, das ist / ein maß von 10. schuhen neme / vnd den schuch in 10. Zoll theilete. Dann man also durch ein einige division ohne mühesame außrechnung der brüche / zu gleich die decempedas, schuhe vnd zoll haben kan. Als in vorhabendem grundriß / wann in dem Triangel DGE. die seit DE. 14. decempedas hielte / wirdt EG. nach der Regel Detri also gesucht. Zu anfang steht der radius DE. 10000000. in der mitte GE. 24142136. als Tangens deß winckels GDE. zu letzt stehn 14. decempedae, als die bekandte seit DE. Auß multiplication deß letztern mit dem mitlern kommen 337989904. dieselben mit 10000000. dem vordern zu dividirn / werden nur die siben letzten ziffer darvon abgeschnitten / weil der divisor soviel nulla hat / also:

33	7989904	.
1	0000000

Kommen also zum Quotienten erstlich 33. decempedae: darnach vnder den abgeschnittenen zahlen die erste zur lincken / nemblich 7. weil sie 10. vnder sich zum Nenner hat / bedeutet sie ${\tfrac {7}{10}}.$ einer decempedae, das ist / 7. schuch. Item die volgend andere zahl 9. weil sie / als Zehler / vnter sich 100. zum Nenner hat / bedeutet sie ${\tfrac {9}{100}}.$ einer decempedae, das ist / 9. Zoll. So man auch noch genawer suchen / vnd ein jeden Zoll / in 10. erste scrupel / ein jed erstes in 10. andere / etc. eintheilen wolte: so würden 8. als die dritte ziffer in der abgeschnittenen zahl / bedeuten ${\tfrac {8}{1000}}.$ von einer decempeda, das seint 8. erste scrupel eines Zolls: Item die volgende 9. weren ${\tfrac {9}{10000}}.$ einer decempedae, oder 9. andere scrupel eines Zolls / vnd so fortan. Also das die seit GE. auffs genaweste gerechnet / helt 33. decemp. 7. schuh / 9. Zoll. 8′. 9′′. 9′′′. 0′′′′. 4′′′′′.

Von dieser rechnung durch zehentheilige vielfaltig continuirte brüch findet man außführlichen bericht in D. Johann-Hartman Beyern newen vollkommenen Visierkunst / im Jahr 1603. zu Franckfurt am Mayn außgangen: vnd ist nicht allein sehr genaw vnd gewiß / sondern auch gantz leicht vnd richtig: vnd weil sie kein newe praecepta (außgenommen die bezeichnuß der Scrupeln belangent) erfordert / sondern mit gemeiner rechnung vbereinkommet / der Astronomischen Logistic weit vorzuziehen / als die vmb viel lang- vnd mühsamer / auch ohne hülff der so genandten tabulae sexagenariae nicht mag verricht werden: also das diese vieleicht gar fallen möchte / wann jene / als noch der zeit new vnd bißher vngewohnliche art / mehrers in übung kommen würde.

Zum andern / das Altimetrische Exempel belangent / mögen in beygefügter figur etliche vnterschiedliche dimensiones gewisen werden. Als

Erstlich / wann AB. als die höhe deß Thurns abzumessen begert / vnd die weite BG. 150. schuch für bekandt angeben würde: muß man erstlich durch einen Quadranten / (so entweder ligent / wie allhie vorgebildet: oder hangent / wie sonsten üblich / mag gebraucht werden) die grösse deß winckels AGB. oder IGH. erforschen / die seye 44°.8′. vnd also sein Complement BAG. oder IGK. 45°.52′. Darnach schliesset man eintweder nach der 5. Regel also: 7177213. (als der Sinus deß winckels BAG. 45°.52′.) gibt die entgegenstehende seit BG. 150. schuh / derhalben werden 6963305. (als der sinus deß winckels AGB. 44°.8′.) geben die auch entgegenstehende seit AB. 145${\tfrac {1}{2}}.$ schuh. Oder aber / nach der 1. Regel vmb viel leichter / also: wie sich verhelt radius GB. 10000000. gegen BA. 9701962. der tangente deß winckels AGB. 44°.8′. Also haltet sich die bekandte seit GB. 150. schuh / gegen der gesuchten höhe BA. 145${\tfrac {1}{2}}.$ schuh.

Zum andern kan auß obgemelten datis die hypotenusa AG. auch auff zweyerley weiß gesucht werden: nemblich entweder durch die 5. Regel also: Wie sich verhalten 7177213. (als der sinus deß winckels BAG. 45°.52′.) gegen BG. 150. schuh / also halten sich 10000000. radius oder sinus deß geraden winckels ABG. 90. gegen AG. 209. schuh. Oder aber viel leichter durch die 1. Regel / also: Radius BG. 10000000. gibt GA. 13932985. die secantem deß winckels AGB. 44°.8′. So wirdt die bekandte weite BG. 150. schuh geben die hypotenusam GA. 209. schuh.

Zum dritten so die höhe AB. 145${\tfrac {1}{2}}.$ bekandt / vnd darauß die weite BG. zuerforschen were / wirdt nur die operation der ersten dimension vmbgekehrt / vnd auch auff zweyerley weiß procedirt / wie daselbsten / also:

Wie sich hal- ten

$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$

6963305. sin. deß winckels AGB.

$\left.{\begin{aligned}\\\\\\\end{aligned}}\right\}$

ge- gen

$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$

145${\tfrac {1}{2}}.$ AB.

$\left.{\begin{aligned}\\\\\\\end{aligned}}\right\}$

Al- so

$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$

7177213 sin. deß winck. BAG.

$\left.{\begin{aligned}\\\\\\\end{aligned}}\right\}$

gegen BG. 150. schu.

10000000 rad. AB.

10307194 BG. tang. deß win. BAG.

145${\tfrac {1}{2}}.$ AB.

Zum vierdten / so die distantz BG. nicht gantz / sondern nur ein theil derselben / als CG. 80. schuh bekandt / vnnd man durch BC. wegen pfützen / gräben oder ander verhindernuß nicht köndte kommen / wirdt solcher vbrige theil BC. also in kundtschafft gebracht. Erstlich bey beeden stenden C. vnd G. neme man die winckel mit dem Quadranten / die kommen bey dem ersten stand G. wie droben: Nemblich / AGB. 44°.8′. vnd GAB. 45°.52′. Bey dem andern stand C. aber soll der winckel ACB. (oder auff dem Quadranten

ECD.) sein von 64°.15′. vnd also sein complement CAB. (oder ECF.) 25°.45′. Darnach subtrahir man BC. 4823427. als die tangentem deß winckels CAB. 25°.45′. Von BG. 10307194. als der tangente deß winckels GAB. 45°.52′. restieren 5483767. welches ist CG. die differentz dieser zweyen tangenten. Entlich wirdt also geschlossen: Wie sich halten 5483767. GC. erstgemelte differentz beyder tangenten, gegen CB. 4823427. der kleinern tangent: also haltet sich der bekandte theil GC. 80. schuh gegen dem gesuchten CB. 70. schuh. So nun GC. 80. zu CB. 70. addirt werden / kombt die gantze distantz GB. 150. schuh / darauß dann hernach die höhe BA. nach obstehender ersten dimension zufinden.

Wiewol fürs fünffte / in solchem casu nicht eben vonnöten / die gantze distantz GB. zu wissen: sondern die höhe BA. auch ohne wissenschafft deß vbrigen theils CB. solcher gestalt kan erfahren werden: Wie sich halten GC. 5483767. (als die vorgefundene differentz beeder tangenten BC. vnd BG.) gegen BA. 10000000. dem radio: also halten sich GC. 80. schuh / gegen BA. 145${\tfrac {1}{2}}.$ schuh.

Zum sechsten / auß dem bekandten theil GC. 80. schuh wirdt die hypotenusa AC. oder AG. also gesucht. Die winckel verbleiben / wie droben: vnnd subtrahiret man erstlich ACB. 64°.15′. Von dem semicirculo 180°. restieret ACG. 115°.45′. darzu addiere AGC. 44°.8′. Summa 160°.53′. die ziehe ab vom semicirculo 180°. restieret der dritte winckel CAG. 19°.7′. Weil nun im Triangel ACG. alle winckel / vnnd darneben auch die seite CG. bekandt / werden nach der 5. Regel auch die andern zwo seiten also gesucht: Wie sich halten 3274928. der sinus CAG. 19°.7′. gegen CG. 80. schuh.

Also halten sich auch	$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$	9006982. der sinus ACG. 115°.45′. (das ist / seines Complements 64°.15′.)	$\left.{\begin{aligned}\\\\\\\end{aligned}}\right\}$	gegen der hy- pote- nusa	$\left\{{\begin{aligned}\\\\\\\end{aligned}}\right.$	AG. 220. schuch.
		6963305. der sinus AGC. 44°.8′.				AC. 170. schuch.

Vnd soviel sey dißmal genug von den tabulis Sinuum vnd jhrem gebrauch berichtet. Ob solches zwar etwas außführlicher hette beschehen sollen vnd können: jedoch ist die form des Handbüchlins in acht zunehmen gewest: Vnd wirdt hoffentlich auch auß dieser kürtze der Künstliebende günstige Leser soviel vernemen künnen / das er anleitung habe / den sachen weiter nachzudencken: wirdt jhme auch die praxis vnd tägliche vbung allerhand vörtel an die Hand geben. Davon zwar auch obverstandener massen zur andern glegenheit mit mehrerm solle gehandlet werden: damit / wie bey vns in vnserer Muttersprach dergleichen nutzliche Künste an tag / vnd den jenigen an die Hand gereicht werden / so in mangel zeit vnd vnkosten / oder anderer verhindernussen halber andere Sprachen / vnd die darinn beschribene Scientias nicht erlernen mögen.

Taflen /

Darinn die

genandte Sinus,

Tangentes vnd Secantes begriffen /

Auff den Radium von

10000000. theilen / vnd erste Scrupula deß Quadranten gerichtet.

[Vignette]

Gedruckt zu Straßburg / durch

Antonium Bertram / in verlegung Pauli Ledertz / Anno 1619.

0	Sinus	Tangens	Secans
1	2909	2909	10000000
2	5818	5818	10000002
3	8727	8727	10000004
4	11636	11636	10000007
5	14544	14544	10000011
6	17453	17453	10000015
7	20362	20362	10000021
8	23271	23271	10000027
9	26180	26180	10000034
10	29089	29089	10000042
11	31998	31998	10000051
12	34906	34907	10000061
13	37815	37816	10000071
14	40724	40725	10000083
15	43633	43633	10000095
16	46542	46542	10000108
17	49451	49451	10000122
18	52360	52360	10000137
19	55268	55269	10000153
20	58177	58178	10000169
21	61086	61087	10000187
22	63995	63996	10000205
23	66904	66905	10000224
24	69813	69814	10000244
25	72721	72723	10000264
26	75630	75632	10000286
27	78539	78541	10000308
28	81448	81450	10000332
29	84357	84360	10000356
30	87265	87269	10000381

WS: Diese Seite zeigt den Beginn der Sinustafeln als Beispiel, der Rest der Tafeln wurde nicht transkribiert.

Tetragonische Tafel /

sambt bericht /

Wie durch

hülff derselben / die

Quadratwurtzeln auß

vorgebenen gevierdten zahlen behend vnd leichtlich zufinden seyen.

[Vignette]

Gedruckt zu Straßburg / durch

Antonium Bertram / in verlegung Pauli Ledertz / im Jahr 1619.

Bericht von der Tetragonischen Tafel.

Wie nit allein hochnützlich / sondern auch gantz notwendig die erfindung der Quadrat- vnnd Cubicwurtzel in allen Mathematischen Künsten seye / ist genugsam bekandt / vnd also diß orts zuerweisen ohne not. Gleich wie aber in andern stucken der Rechenkunst allerhand nützliche Compendia, zur behendigkeit dienstlich / erfunden worden: also haben sich auch hierinn etliche bemühet / einen leichtern richtigern weg beyderleyer extraction zuersinnen. Wie dann vor diesem Joannes Antonius Maginus in einem sondern Buch von behender erfindung der Quadratwurtzel: Christophorus Clavius aber zu ende seiner geometria practica von erforschung der so wol Quadrat- als cubicwurtzel / auß gewissen Taflen / berichtet haben. Vnd ob wol die Rechenkunst in vnser Muttersprach sehr hoch kommen: ist doch meines wissens von diesem Compendio niemalen ichtes in derselben geschrieben worden. Ist derwegen vor gut eracht worden / denen Teutschen liebhabern der Mathematic zu nutz / gemelte Taflen diesem Handbüchlein beyzufügen: auch derselben gebrauch mit kurtzem / vnd / so viel müglich / deutlichem bericht vor augen zustellen.

Was nun erstlich die Tetragonische oder Quadrattafel belanget / (welche in obgemeltem tractatu Magini, von R. 1. biß R. 10000. steht: allhie aber / das vacierende Papier zufüllen / biß auff R.11100. hat müssen außgerechnet werden) ist anfänglich mit wenigem zumelden / auß was fundament dieselbe gerechnet worden: Damit / wann es einem beliebte / er dieselb zu seinem nutz continuirn, vnd auff grössere wurtzlen erweitern möge.

Vnd ist zwar nicht ohn / wann man ein zahl / als wurtzel / in sich selbst multipliciert / das jhr quadrat darauß entspringe. Weil aber solche multiplication / bevorab in grössern zahlen / nicht wenig beschwerlich ist / mag nachvolgendes Compendium an statt derselben gebraucht werden. Setze anfenglich in der ersten zeil (wie in beygesetzem täfelin zusehen) die wurtzlen in natürlicher ordnung nacheinander / so viel man deren begert. Darnach in der andern zeil setz die Progression der vngeraden zahlen / von 3. an / mit der differentz 2. auffsteigent. Welche zahlen nichts anders seint / als Gnonomes, vnd differentien / zwischen zweyen nechst- oder benachtbarten quadraten.

Wurtzel	Gnomones	Quadrat
1 2 3	3 5 7	1 4 9
4 5 6	9 11 13	16 25 36
7 8 9	15 17 19	49 64 81
10 11 12	21 23 25	100 121 144

Daraus dann fürs dritte die Quadrat (so in der dritten zeil) also gefunden werden. Zu dem ersten quadrat 1. addier den in der anderen zeil neben ihm stehenden Gnomonem 3. darauß entspringt das andere quadrat 4. darzu addier den anderen Gnomonem 5. gibt das dritte quadrat 9. Vnd also fortan / so man ein quadrat mit dem nebenstehenden gnomone addirt / erwechst allezeit das nechst volgende quadrat.

R. 1	1 3
2	4 5
3	9 7
4	16 9
5	25 11
6	36 13
7	49

Zwar nicht eben vonnöten / das die gnomones neben den Quadraten stehn: sondern man kan sie füglicher addition halber also vntereinander setzen / wie hieneben zusehen.

Wann nun einer die nachgesetzte Tetragonische Tafel auff solche weiß vber 11100. hinauß weiter fortrechnen wolte / muß er erstlich den gnomonem finden / der zu dem letzten quadrat addirt / das nechst grössere gibt. Es haben aber die quadratzahlen ein solche art / wann mann jhr wurtzel dupliert / vnd zu dem duplat 1. addirt / so ist solches ihr gnomon, der darzu addirt / das nechstgrössere quadrat gibet. Weil nun in diesen Taflen 11100. die letzte wurtzel ist / so duplier dieselb / vnd addiere 1. werden 22201. solcher gnomon zu dem letzten quadrat 123210000 addirt / gibt das volgende quadrat 123232201. dessen wurtzel 11101. Gemelten gnomonem 22201. continuire / in seiner vngeraden mit 2. auffsteigenden Progression / vnd addiere solche gnomones zu den quadraten / wie droben / vnd auß dieser tabella zusehen.

Wurtzel	Gnom.	Quadrat
11100	22201	123210000
11101	22203	123232201
11102	22205	123254404
11103	22207	123276609
11104	22209	123298816
11105	22211	123321025
11106	22213	123343236
etc.

Oder in praxi also:
123)	210000 22201
	232201 22203
	254404 22205
	276609 22207
	298816 22209
	321025 22211
	343236

Hievon aber sey genug. Volgen etliche Canones, wie solche Taflen nutzlich zugebrauchen.

Die erste Regel.

Wie man das Quadrat einer jeden zahl / so nicht vber 11100. ist / aus der Tetragonischen Tafel suchen soll.

Es ist die structura vnd außtheilung dieser Tafel also angestelt / das zu öberst vberzwerch / vnd auff der lincken seiten abwertz die Quadratwurtzeln dergestalt verzeichnet stehn / das oben die centenarij, (das ist / die jenige zahlen / so mit 100. auffgehn) vnd auff der seit / was vnter 100. ist / gesetzt wirdt: In der Tafel aber selbsten / oder in der feldung / stehn die Quadratzahlen derselben wurtzlen. So derwegen ein Quadratwurtzel vorgeben / vnd dessen Quadrat zu wissen begert wirdt / so nim derselben jhre Centenarios oben / vnd was vnter 100. ist / auff der lincken seiten / so wirstu in gemeinem winckel der Tafel das begerte Quadrat finden. Zum Exempel / man begert zu wissen / was die wurtzel 1240. für ein quadrat habe. Die Centenarios, nemblich 1200. nim in der öbersten vberzwerchen / die 40. aber in der lincken absteigenden seit: Vnd wo die linien / deren eine von den Centenarijs 1200. vnterwerts / die ander von 40. vberzwerch gezogen wirdt / zusammen stossen / allda ist der gemeine winckel / so das begerte quadrat / nemblich 1537600. in sich haltet.

Wo aber die vorgebene wurtzel keine Centenarios in sich hielte / als wann das quadrat der wurtzel 63. begert würde / wirdt also gesucht: oben nun die figur 0. vnd auff der seit 63. so wirdt der gemeine winckel geben das quadrat 3969.

Im fall die vorgebene wurtzel grösser were als 11100. muß jhr quadrat durch multiplication in sich selbst / wie sonsten gebreuchlich: oder aber auß diesen Taflen solcher gestalt gesucht werden. Die vorgebene wurtzel dividier mit 2. 3. 4. oder einer andern zahl / dardurch sie auffgeht. Deß quotienten Quadrat nim auß der Tafel: solches quadrat multiplicier mit dem quadrat deß theilers: was kombt / ist das quadrat der vorgebenen zahl. Als / weil die wurtzel 23685. nicht in der Tafel begriffen / so dividiere sie mit 3. deß quotienten 7895. quadrat wirdt in der Tafel gefunden 62331025. dieses multiplicier mit dem quadrat deß theilers 3. nemblich mit 9. kommen 560979225. welches ist das eigentliche quadrat der vorgebenen wurtzel 23685.

Die ander Regel.

Wie man die Quadratwurtzel auß einer jeden zahl so nicht vber 123210000. ist / solle außziehen.

Ein jede zahl ist entweder ein perfect vnd vollkommenes Quadrat / dessen eigentliche gewisse wurtzel man haben kan: oder aber sie ist ein surdus numerus, deren rechte vnfählbare Quadratwurtzel man nicht kan finden / sondern man muß sich mit einer wurtzel begnügen lassen / die sich der rechten zimblichen nachöhmet. In beeden arten wirdt also Procedirt. Erstlich theile die vorhabende zahl ab in jhre begriff / also das zur rechten hand angefangen / vnd je nach zweyen Ziffern ein strichlein gemacht werde. Welches darzu dienet / damit man in der Tetragonischen Tafel desto behender nachschlagen möge. Dann soviel derselben begriffe seind / soviel ziffer wirdt auch die Quadratwurtzel haben. Zum andern vorhabende zahl suche in der feldung der Tetragonischen Tafel / vmb dieselbe gegend / da die wurtzlen von soviel Ziffern stehn / als viel man begriff hat: oder / da die quadrat seint / die eben von soviel Ziffern vnd deß anfangs / wie das deinige. So nun eben dein zahl in der Tafel steht / ist sie ein rechtes Quadrat: dessen wurtzel ist die zahl / so zusammen gesetzt wirdt auß den zu oberst stehenden Centenarijs, vnd der andern zahl vnter 100. so nebens auff der lincken seiten steht.

Zum Exempel / es wirdt begert / auß 14784025. die Quadratwurtzel zu suchen. Theil erstlich die zahl in jhre begriff also: 14|78|40|25 / Weil sie nun vier begriff vnd 8. Ziffer hat / so suche sie vmb dieselbe gegend / da die wurtzel von 4. Ziffern / vnd die quadrat von 8. Ziffern mit 14. anfangend stehen / so wirstu vorhabende zahl just stehend finden / vnter den Centenarijs 3800. vnd auff der lincken seit neben sich habend 45. Welche zwo zahlen / nemblich 3800. vnd 45. zusammen gesetzt / geben 3845. die eigentliche wurtzel deß vorhabenden Quadrats 14784025.

Wann aber die auffgebene zahl nicht vollkommen in der Tafel gefunden würde / ists ein anzeigung / das solches ein surdus numerus, vnd nicht recht geviert seye: dessen nahene wurtzel (dann die eigentliche nummer gefunden werden kan) zu suchen / halte volgenden proceß. Nim das nechst kleinere quadrat / sambt seiner wurtzel / solcher gestalt / wie vor. Dieser gefundenen wurtzel wird ein Fraction angehenckt: die also zu suchen. Subtrahier jetzt gemeltes nechstkleineres quadrat von dem deinigen. Was bleibt / ist der zehler. Darnach duplier erstgedachte wurtzel: vnd zu dem duplat addiere 1. Solche summa ist der Nenner. Dieser bruch zu der vorgefundenen wurtzel von gantzen zahlen gethan / macht die wurtzel der auffgebenen Surdischen zahl: die zwar nicht gantz vnd eigentlich / sondern allezeit vmb etwas zu wenig ist. Deßwegen dann auch / wann sie in sich selbst multiplicieret wirdt / das product allezeit etwas kleiner / als die auffgebene zahl / befunden wirdt: aber der abgang so gering / das er keinen mercklichen jrrthum bringen kan. Als es wirdt zu suchen begert die nahene wurtzel dieser surdischen zahl 18981357. vnd weil diese nicht selbst in der Tafel steht / so nime das nechst kleinere quadrat / so darinn begriffen / nemblich 18974736. dessen wurtzel ist 4356. Darnach subtrahiere solch nechst kleineres quadrat von deiner vorhabenden zahl: restieren 6621. welchs ist der zehler. Entlich duplier die gefundene wurtzel 4356. vnd zu dem duplat 8712. addiere 1. werden 8713. der Nenner: vnd also dieser bruch: ${\tfrac {6622}{8713}}.$ welcher zu gemelten 4356. gethan / bringen $4356{\tfrac {6621}{8713}}.$ die nahene wurtzel der auffgebenen surdischen zahl 18981357.

So man aber solche gebrochene zahl in einer andern benennung / als von 100. 1000. etc. haben wolte / so multiplicier den zehler mit dem begerten newen Nenner / als mit 100. oder 1000. etc. das product dividiere mit dem alten Nenner: der Quotient ist der newe zehler / vnd 100. oder 1000. oder womit multiplicirt worden ist / der newe Nenner. Als in vorigem Exempel / der zehler 6621. mit 1000. multiplicirt / ist 6621000. diß dividiere mit dem Nenner 8713. kommen 759. (was in der division vberbleibt / ist nicht zu achten) Ist also die newe / der vorigen gleichgeltende / vnd zur benennung von 1000. reducirte fraction ${\tfrac {759}{1000}}.$ die zu den gantzen zahlen gesetzt / bringt $4356.{\tfrac {759}{1000}}.$ die nahene wurtzel vorhabender surdischen zahl.

Die dritte Regel.

Wie auß einer kleinen surdischen zahl die nahene wurtzel zu finden.

Der andere theil obgesetzter Regel kan zwar auch hierzu gebraucht werden. Aber doch kan man die wurtzel viel neher vnd eigentlicher bekommen auff nachvolgende weiß. 1. Vorgebene kleine zahl mehre mit einem / zweyen oder mehr par circuln oder nulla / als 00. 0000. 000000. doch also / das die zahl nicht vber 123210000. (welchs ist das gröste quadrat dieser Tafel) erwachse. 2. Die Quadratwurtzel dieser vermehrten zahl such auß der Tafel nach obgesetzter Regel. 3. Von solcher gefundenen wurtzel wirff zur rechten hand soviel figuren hinweg / als viel par circuln zuvor zur auffgebnen zahl hinzu gesetzt worden seint. Diese hinweg geworffene zahl ist der Zeler: der Nenner aber ist entweder 10. so nur ein par / oder 100. so zwey / oder 1000. so drey par circuln hinzu gethan worden seint.

Es sey die auffgebene zahl 8. darauß die Quadratwurtzel nach der obstehenden 2. Regel gezogen / ist $2{\tfrac {4}{5}}.$ Aber so man zu solcher zahl noch drey par circuln setzt / also / 8|00|00|00| vnd in der Tafel die nahene wurtzel dieser vermehrten zahl suchet / welche allhie ist 2828. (NB. den rest der Subtraction der nechst kleinern zahl von der vorhabenden pflegt man in dieser operation nicht zu achten / es sey dann / das solcher rest grösser were / als die wurtzel / dann in solchem fall kan man die wurtzel vmb ein vnitet vermehren) von solcher wurtzel die drey letzten figurn 828. absündert / vnd an statt deß Zehlers: an des Nenners aber 1000. setzet: (weil drey par circuln zuvor hinzu gesetzt worden) vnd solche fraction zu der vbrigen zahl 2. setzet / so bekommet man viel ein nehere^[16] vnd eigentlichere Quadratwurtzel der vorgebenen surdischen zahl 8. als durch vorige Regel / nemlich $2{\tfrac {828}{1000}}$. Darbey zu mercken / das solche vermehrung mit hinzusetzung der Circuln nicht allein bey dergleichen kleinen / sondern auch grössern surdischen zahlen mit nutz^[17] zugebrauchen: vnd je mehr par der circuln addirt werden / je genawer auch die wurtzel kombt. Allein weil auff solche weiß die zahl vber 123210000. als das gröste Quadrat vnserer Tafel erwachst / kan die operation durch vorhabende Regel allein nicht verricht werden: sondern es muß nachvolgende zu hülff genommen werden.

Die vierdte Regel.

Wie man die Quadratwurtzel auß einer zahl / die vber 123210000. ist / durch hülff der Tetragonischen Tafel außziehen soll.

Die Tetragonische Tafel ist eigentlich nur auff die jenigen zahlen gerichtet / so vnter 123210000. seint. Im fall aber ein grössere zahl zu resolvirn vorkeme / so theilt man erstlich dieselbe ab in jhre begriff / wie droben gelehrt. Darnach nimbt man die ersten vier / vnd bißweilen auch fünff begriff zur lincken hand / (nemblich welche nicht mehr halten / als obgemeltes gröste Quadrat der Tetragonischen Tafel) die vbrigen begriff aber zur rechten werden abgeschnitten / vnd auff weitern bescheid behalten. Zum dritten die nach dem abschnit noch vberbleibende begriff / als Quadrat / suche in der Tetragonischen Tafel nach anweisung der anderen Regel: dieselbe wurtzel verzeichne zum Quotienten: vnd im fall die vorhabende zahl nicht völlig in der Tafel steht / so nim die nechst kleinere / vnd subtrahiere sie von der vorhabenden. Fürs vierdte auß dem abschnit vnd noch restierenden zahlen die wurtzel zu extrahirn / ob wol Maginus ein andere art gebraucht / die hernach soll angezeigt werden: ist doch am allersicher- vnd gewissesten / es beschehe solches durch die gnomonische division / wie sonsten in gemeiner extraction gebreuchlichen / also. 1. Duplier den gantzen Quotienten: deß duplats erste ziffer zur rechten hand setze vnter die letzte ziffer deß vorstehenden begriffs zur lincken / vnd schreibe die volgenden jmmer ordentlich fort gegen der lincken hand hinauß vnter den rest der obgemelten subtraction. Vnd dieses duplat ist der Theiler.

2. Durch diesen Theiler dividiere die richtig obgeschribene zahl / doch der gestalt / das die zahl / welche da erwächst auß multiplicierung deß Theilers vnd beygefügten ziffer deß Quotienten / durch den letzten Quotient / nicht grösser werde / als die obgezeichnete zahl. Diesen Quotienten der theilung schreibe zu den vorigen ziffern deß Quotienten.

3. Eben diesen Quotienten setze vnter die erste ziffer deß vorstehenden begriffs bey der rechten hand.

4. Mit diesem letzt gefundenen Quotienten multipliciere den Theiler / sambt seinem beygefügten Quotienten / als wanns eine zahl were: was da kombt / subtrahir von der obgeschribenen zahl. Dieser gestalt verfahre ordentlich bey allen volgenden begriffen. Zum Exempel / die wurtzel auß 135979736849. zu extrahiren / so werden erstlich die vier ersten begriff / nemblich 13|59|79|73| in der Tafel nachgeschlagen / vnd zwar nicht gantz / aber doch das nechst kleinere Quadrat 13593969. vnter der wurtzel 3687. gefunden vnd von vorhabender zahl abgezogen: bleibt per resto 4004. steht in der operation also:

		4	4
13	59	79	73	37	68	49 (3687
13	59	39	69

Ferner auß diesem rest vnd vbrigen vorbehaltenen drey begriffen 37|68|49| vnd erstlich zwar auß dem volgenden begriff vnnd zugehörigem rest / nemblich auß 4004|37| die wurtzel durch gnomonische division zu extrahirn / so duplier anfänglich den gantzen Quotienten / nemblich die vorgefundene wurtzel 3687 werden 7374. dieses duplat schreibe vnter deß vorstehenden begriffs letzte ziffer 3. vnnd jhre zugehörigen restierende. Durch eben diß duplat theile die obgeschriebene zahl: den gefundenen Quotienten 5. schreib beydes zu denen vorigen Quotienten / vnd auch neben den Theiler / vnter die 7. Letzlich multipliciere den theiler vnd sein beygefügte ziffer durch diesen Quotienten / nemblich 73745. durch 5. so kommen 368725. die subtrahire von denen obgeschribenen 400437. vnd bleiben 31712. steht also:

			7
		43	14	12
23	59	79	73	37	68	49 (36875
23	59	39	69
		7	37	45
				5
		36	78	25

Volgender begriff vnd gehöriger rest / ist 31712|68| vnd wirdt allerdings / wie der vorige resolvirt / das man nemblich den gantzen Quotienten 36875. dupliere: das duplat 73750. vnter deß begriffs letzte ziffer 6. vnd anhangenden rest schreibe: damit die obgeschriebene zahl 3171268. dividiere: den Quotienten 4. zu denen vorigen Quotienten / wie denn auch neben dem Theiler / vnter 8. zeichne: den Theiler / sambt seiner jetzt beygefügten ziffer / durch diesen letzten Quotienten multipliciere: das product 2950016. von der obgeschriebenen zahl 3171268. abziehe / bleiben über / 221252. welche mit volgenden letztem begriff |49| noch zu resolvirn vberig / allermassen wie vor / nemblich durch deß gantzen Quotientens duplat 737508. dividier gemelten rest: den Quotienten 3. schreib zu dem vorigen Quotienten / vnd auch neben das duplat / vnter 9. Durch diesen letzten Quotienten 3. multiplicier das duplat vnd beygefügte ziffer: das product 22125249. von obgeschribener zahl ziehe ab: so bleibt nichts vbrig. Darauß erscheint / das die auffgebene zahl ein recht quadrat oder gevierdte zahl seye / deren eigentliche wurtzel 3687543. Besihe die operation

			2
			27
		43	14	12	52
23	59	79	73	37	68	49	(3687543
23	59	39	69
		7	37	45
				5
		36	87	25
			73	75	04
					4
		2	95	00	16
			7	37	50	83
						3
			22	12	52	49

Volgt auch ein Exempel einer surdischen zahl / in deren man die fünff erste begriff in der Tafel nachschlagen kan: die seye 120627211573894. welche allermassen / wie vor / resolvirt / vnnd jhre nahene wurtzel $10983042{\tfrac {130}{21966085}}.$ gefunden wirdt / wie auß beygefügter description zusehen.

				43		1
			9	22	93	22	3
1	20	62	72	11	57	38	94	$(10983042{\tfrac {130}{21966085}}$
1	20	62	62	89
			21	96	60
			2	19	66	04
						4
			8	78	64	16	32
				21	96	60	2
				43	93	22	64

Was droben zu ende der 3. Regel gemeldet worden / kan auß volgendem Exempel verstanden werden. Auß surdischer zahl 635. die nahene wurtzel zu extrahirn / thue zu derselben etliche par circuln / als 63500000000. dieser vermehrten zahlen wurtzel ist 251992. (was bey der extraction vberbleibet / wirdt nicht geacht) vnd weil die auffgab zwen begriff hat / so werden von solchen Quotienten nur die zwo ersten zahlen 25. behalten: die vbrigen aber 1992. seint der Zehler / vnd 10000. der Nenner: nemblich von vier circuln / weil vier par circuln vorhin auffgebener zahl zugefügt worden.

		1	3	1
		46	39	99	36
6	35	00	00	00	00	$(25{\tfrac {1992}{10000}}$
6	34	53	61
		5	03	8$_{9}^{9}$
		45	35	01
			50	39	$_{\ 2}^{82}$
		1	00	79	64

Maginus lehret an statt der gnomonischen division ein anders compendium / man solle die vier (oder in dieser erweiterten Tafel bißweilen auch fünff) erste begriff in der Tafel nachschlagen / davon das nechst kleinere darinn begriffene quadrat abziehen (in massen auch droben gelehrt) zu dem rest soviel circuln addirn / als viel begriff abgeschnitten worden: das gefundene nechst kleiner Quadrat von dem nechst grössern abziehen (oder / welches eines ist / die wurtzel deß nechst kleinern Quadrats dupliern: zu dem duplat 1. addirn) mit diesem rest oder duplat vorigen rest vnd beygefügte circuln dividirn: den Quotienten zu vorgefundener wurtzel deß nechst kleinern Quadrats setzen.

Es hat aber diese art / neben dem / das sie in grossen zahlen ohn mercklichen Irrthumb nicht zugebrauchen / auch diese vngelegenheit / das dadurch auß einer kleinern / vnd also viel mehr grössern recht gevierten zahl die rechte Quadratwurtzel nicht gefunden wirdt. Als in vnserm ersten Exempel 13597973376849. so ein recht Quadrat / vnd sein eigentliche wurtzel 3687543. ist / wirdt doch durch diesen proceß mehr nicht als 3687542. gefunden / wie hierauß zusehen.

		4	4
23	59	79	73	37	68	49	(3683	$\left.{\begin{aligned}\\\\\\\\\\\\\\\end{aligned}}\right\}$
23	59	29	69
				6
				327
				31655
				4004000			(542
				737558
				7377
				73

Das also rahtsamer / bey gewöhnlicher gnomonischer division zuverbleiben / biß was bessers erfunden wirdt.

Tetragonische Taflen.

	0	100	200	300	400	500
0	0	10000	40000	90000	160000	250000
1	1	10201	40401	90601	160801	251001
2	4	10404	40804	91204	161604	252004
3	9	10609	41209	91809	162409	253009
4	16	10816	41616	92416	163216	254016
5	25	11025	42025	93025	164025	255025
6	36	11236	42436	93636	164836	256036
7	49	11449	42849	94249	165649	257049
8	64	11664	43264	94864	166464	258064
9	81	11881	43681	95481	167281	259081
10	100	12100	44100	96100	168100	260100
11	121	12321	44521	96721	168921	261121
12	144	12544	44944	97344	169744	262144
13	169	12769	45369	97969	170569	263169
14	196	12996	45796	98596	171396	264196
15	225	13225	46225	99225	172225	265225
16	256	13456	46656	99856	173056	266256
17	289	13689	47089	100489	173889	267289
18	324	13924	47524	101124	174724	268324
19	361	14161	47961	101761	175561	269361
20	400	14400	48400	102400	176400	270400
21	441	14641	48841	103041	177241	271441
22	484	14884	49284	103684	178084	272484
23	529	15129	49729	104329	178929	273529
24	576	15376	50176	104976	179776	274576
25	625	15625	50625	105625	180625	275625
26	676	15876	51076	106276	181476	276676
27	729	16129	51529	106929	182329	277729
28	784	16384	51984	107584	183184	278784
29	841	16641	52441	108241	184041	279841
30	900	16900	52900	108900	184900	280900
31	961	17161	53361	109561	185761	281961
32	1024	17424	53824	110224	186624	283024

WS: Diese Seite zeigt den Beginn der Tetragonischen Tafeln als Beispiel, der Rest wurde nicht transkribiert.

Cubic Tafeln /

Sambt kurtzem

vnterricht / wie

durch hülff derselben / auß

einer vorgebenen Cubischen zahl / die Wurtzel behend außzuziehen seye.

[Vignette]

Gedruckt zu Straßburg /

durch Antonium Bertram / in verlegung Pauli Ledertz. Anno M. DC. XIX.

Bericht vom gebrauch volgender Cubictaflen.

Es wirdt in diesen Taflen nachgeschlagen / vnd der Cubus einer jeden zahlen / so vnter 1000. ist / gesucht / allerdings wie droben von den Quadraten in der ersten Regel gelehrt. Ist also ohnnot / hievon mehrers zu melden.

Vnd nach dem diese Taflen nur auff die Cubicwurtzlen von 1. biß 1000. gericht / wofern einer dieselben zu seinem gebrauch erweitern wolte: thue ers solcher gestalt. Die vorhabende zahlen / als Cubicwurtzlen / multiplicier durch jhre Quadrata (die man dann auß voriger Tetragonischen Tafel von 1. biß 11100. zum besten haben kan) so entspringen darauß jhre Cubi. Als / so man die wurtzel 1240. mit jhrem Quadrat 1537600. multipliciert / kombt jhr Cubus 1906624000.

Man kan aber die sach kürtzer begreiffen durch volgendes mittel. Gleich wie die Quadrat daher erwachsen / so man alle vngerade zahlen von 1. natürlicher ordnung auffsteigend / als jhre gnomones / oder differentien / continuè zu den vorhergehenden Quadraten addirt / wie droben gelehrt: Also ist auch bey den Cubis ein solche differentz zufinden / die zu dem vorgehenden Cubo addirt / alsbald den nachvolgenden gibt.

Progreß mit 6. auffsteigent	differentien der Cuben	die Cubi	Wurtzel
6	1	1	1
12	7	8	2
18	19	27	3
24	37	64	4
30	61	125	5
36	91	216	6
42	127	343	7
48	169	512	8
54	217	729	9

etc.

Mach ein Arithmetische progreß von 6. an / so weit vonnöten / deren differentz seye 6. Also: 6. 12. 18. 24. 30. etc. wie in der ersten zeil beygesetzten täfelins zusehen. In der anderen zeil aber werden gesetzet die differentien oder vnderscheid eines jeden Cubi vom andern / mit solcher ordnung. Anfangs neben 6. setze 1. vnd darunter 7. welche zahl entspringt auß^[18] addition deren neben einanderstehenden 6. vnd 1. Vnter diese 7. setz 19. die auß addition 12. vnd 7. erwachsen. Vnd also fortan so man addirt die zwo zahlen / so in der ersten vnd andern zeil neben einander stehn / werden sie geben die nachvolgende oder vntere zahl in der andern zeil. In der dritten zeil werden die Cubi ordenlich nach einander gesetzt / die man durch continuirte addition der zahlen erstgemelter anderen zeil solcher gestalt suchet. Der erste Cubus ist 1. zu deme addier die volgende differentz 7. kombt der andere Cubus 8. zu deme addier die volgende differentz 19. kombt der dritte Cubus 27. vnd also fortan. Endlich in der vierdten zeilen werden ordenlich ihre wurtzlen gesetzt.

Ob die continuation der ersten vnd anderen zeilen recht verrichtet / wirdt also probiert. Vnd anfangs zwar die erste zeil betreffent / ist zu wissen / das ein jede zahl der mit 6. auffsteigenden progression / sechsfach ist gegen der wurtzel deß nebenstehenden Cubi. Als 18. ist sechsfach gegen der wurtzel 3. Item 42. gegen 7. etc.

Darnach die ander zeil betreffent / probirt man sie also: multiplicier mit 3. so wol die vorhabende Cubische wurtzel / als auch jhr quadrat: diese zwey product / vnd ein vnitet addiere: solche Summ ist die differentz deß Cubi der vorhabenden wurtzel vom volgenden Cubo.

Als in obstehendem Täfelin / zu probiern / ob die differentz zu R. 5. gehörig / nemblich 91. recht gesucht worden / so tripliere bedes solche 5. vnd sein quadrat 25. werden 15. vnd 75. addier diese zwey product / vnd 1. werden 91. welches ist Gnomon, oder die differentz deß Cubi von R. 5. von dem volgenden Cubo R. 6.

So man nun diese Tafel vber R. 1000. zu erweitern begert / so muß man suchen erstlich die zal dero mit 6. auffsteigenden progression / zu der letzten wurtzel 1000. gehörig: Solche ist 6000. (nemblich sechsfach gegen der wurtzel / wie kurtz zuvor gemeldet) darnach die differentz deß letzten Cubi 1000000000. vom nachvolgenden: diese ist 3003001. Solche zwo zahlen der progressin vnd differentz continuire / vnd suche drauß die Cubos nach droben gegebener lehr / so weit du wilt. Wie auß beygefügtem Täfelin zuvernemen.

Progreß mit 6. auffsteigent	differentzien der Cuben	die Cubi	wurtzel
6000		1000000000	1000
6006	3003001	1003003001	1001
6012	3009007	1006012008	1002
6018	3015019	1009027027	1003
6024	3021037	1012048064	1004
6030	3027061	1015075125	1005
6036	3033091	1018108216	1006
6042	3039127	1021147343	1007
6048	3045169	1024192512	1008

Soviel nun die extraction der Cubicwurtzel betrifft / theile erstlich die auffgab in jhre begriff / also das du bey der rechten hand anfangest / vnd je nach dreyen ziffern ein strichlein mächest. Soviel deren begriffen seint / soviel ziffer wirdt auch die Cubicwurtzel haben.

2. Die ersten drey begriffe such in der Cubictafel: vnd so sie nicht gantz vorhanden / so nim den nechsten kleinern Cubum / ziehe jhn davon ab.

3. Der rest vnd vbrige begriff werden durch die gnomonische division / wie sonsten gebreuchlich / resolviert / nemblich also:

⁹.^[19] Triplier den gantzen Quotienten: dieses triplats erste ziffer zur rechten hand setz vnter die mitler ziffer deß vorstehenden begriffs / vnd die andern volgende nach einander gegen der lincken.

2. Diß triplat multiplicier durch den gantzen Quotienten: deß products erste ziffer zur rechten setz vnter deß vorhabenden begriffs letzte ziffer zur lincken vnters Triplat: diß product ist der Theiler.

3. Damit dividier die obstehende zahl: doch also / daß das product / welches erwächst auß multiplicierung deß Quotienten mit etlichen volgenden vnderschiedlichen zahlen / nicht grösser werde / als die obgeschribene zahl. Diesen Quotienten verzeichne zu denen vorigen ziffern deß Quotienten.

4. Mit diesem letzten Quotienten multipliciere den Theiler: das product setz vnter den Theiler.

5. Diesen letzten Quotienten quadriere (das ist / multiplicier jhn durch sich selbst) vnd mit diesem quadrat multiplicier das nechste triplat: das product aber setz vnter das triplat.

6. Eben diesen Quotienten multiplicier Cubicè: vnd setze dessen Cubi eusserste ziffer zur rechten / vnter die eusserste ziffer deß vorstehenden begriffs auch bey der rechten hand.

7. Diese drey product addier zusammen: die Summ subtrahier von obgeschribener zahl. Ebenmessig procedier bey allen begriffen. Zum Exempel / auß dem Cubo 643763976149736. die wurtzel zusuchen / theile jhn erstlich in seine begriff / vnd suche die ersten drey begriff in der Cubictafel / die du zwar nicht gantz / aber den nechst kleinern Cubum 642735. 647. vnter der wurtzel 863. findest / den subtrahier von gemelten dreyen begriffen: restieren 1028329. Erstgedachte wurtzel setz an statt deß Quotienten / also:

1	28	329
643	763	976	149	736 (863
642	735	647

Ferner solchen rest vnd volgenden begriff / nemblich 1028329 | 149. durch gnomonische division zu resolvirn / so tripliciere erstlich den Quotienten 863. so sinds 2589. dieses triplats letzte ziffer setz vnter die mitler ziffer dieses begriffs / nemblich vnter 4. vnd die andern vntervolgende. Das triplat 2589. multiplicier durch den gantzen quotienten 863. vnd das product 2234307. schreib vnter 1. als die letzte ziffer dieses begriffs / für den Theiler. Durch diesen Theiler 2234307. dividier die obstehende zahl 1028329149. vnd den quotienten 4. setz zu denen vorigen zahlen deß quotienten 863. mit diesem quotienten 4. multiplicier den Theiler 2234307. das product 8937228. schreib vnter den Theiler. Ferner den quotienten 4. quadriere / werden 16. damit multipliciere das nechst triplat 2589. das product 41424. schreib vnter das triplat. Weiter multiplicier den quotienten 4. cubicè, kombt der Cubus 64. den setz vnter 9. die eusserste ziffer dieses begriffs. Letzlich addiere diese drey product 8937228 / 41424 / vnd 64. die Summ 894137104. subtrahier von obgeschribener zahl 1028329149. bleiben 134192045. die mit dem volgenden letzten begriff |736| noch zu resolvirn vbrig / welchs allermassen / wie bey vorigem begriff geschicht. Nemblich triplier den gantzen quotienten 8634. deß triplats 25902. letzte ziffer setz vnter 3. die mitler ziffer deß vorhabenden begriffs. Eben diß triplat multiplicer durch den gantzen quotienten: vnd das product 223637868. schreib vnter 7. die letzte ziffer dieses begriffs / für den Theiler: dardurch dividiere die obstehende zahl 134192045736. vnd den quotienten 6. setze zu den vorigen zahlen deß quotienten / vnd multipliciere damit den Theiler: das product 1341827208. setze vnter den Theiler. Gemelten quotienten 6. quadriere: mit dem quadrat 36. multiplicier das nechste triplat 25902. das product 932472. schreib vnter das triplat 25902. Ferner den quotienten 6. multiplicier cubicè werden 216. die setz vnter 6. als die eusserste ziffer dieses begriffs zur rechten. Endlich addier diese drey product 1341827208 / 932472 / vnd 216: die Summ 134192045736. subtrahier von der obgeschribenen zahl / so bleibt nichts vbrig. Darauß dann erscheinet / das die angegebene zahl 643763976149736. ein rechte Cubische zahl seye / deren eigentliche wurtzel 86346. welche so sie mit jhrem quadrat 7455631716. multiplicirt wirdt / gemelten Cubum 64376397149736. völlig wider bringt. Der ganzte proceß dieser operation ist auß volgender description zuvernemen.

	34	192
7	128	329	5
643	763	976	149	736	(86346
642	735	647
Tripl.		25	890
Theil.	223	430	700
	893	722	800
		414	240
			64
	894	137	104
Tripl.			259	020
Theil.	22	363	786	800
	134	182	720	800
		9	324	720
				216
	134	192	048	736

Wann aber die zahl nicht recht Cubisch / sondern surdisch were / so wirdt sie erstlich mit etlichen Cubischen oder dreytheiligen Circulbegriffen vermehret / je mehr / je genawer. Darnach auß dieser vermehrten zahl ziehe die Cubicwurtzel eben wie bey den rechten Cubischen zahlen / was letzlich vbrig bleibt laß fahren. Von der gefundenen wurtzel behalt zur lincken so viel ziffer / als viel begriff die auffgab hat: die vbrigen ziffer aber geben den Zehler: der Nenner aber ist entweder 10. so ein begriff / oder 100. so zwen / oder 1000. so drey begriff circuln addiert worden: vnd also fortan hat der Nenner allzeit soviel circuln / als viel begriff derselben zur auffgab gesetzt: allermassen wie bey den quadratzahlen gelehret worden. Zum Exempel auß der surdischen zahl 23. die Cubische wurtzel zu extrahirn / so vermehre sie mit vier begriffen / also 23|000|000|000|000. Dieser vermehrten zahlen wurtzel wirdt nach obstehender lehr gefunden 28437. davon wirdt nur die erste zahl 2. für die gantze wurtzel behalten / weil die auffgab 23 nur einen begriff haltet: die vbrigen aber 8437. seint der Zehler: vnd 10000. der Nenner / nemblich von 4. circuln / weil die vermehrung mit 4. begriffen geschehen: Die operation ist also beschaffen.

		51
	11	28	150
33	98	669	893	547
23	000	000	000	000	$(2{\tfrac {8437}{10000}}$
	909	304
Tripl.		8	520
Theil.	24	196	800
	72	590	400
		76	680
			27
Tripl.	72	667	107
Theil.			85	290
	2	424	794	700
	16	973	562	900
		4	179	210
				343
	26	977	742	453

Das compendium, so Maginus an statt der gebreuchlichen gnomonischen division bey den quadraten erdacht / kan auch auff die Cuben / die viel begriff haben / vnd also die gnomonische division mühsam fellt / solcher gestalt mutatis mutandis gericht werden. Zum Exempel / auß der zahl 23|000|000|000|000|000. such anfangs in der Tafel die wurtzel der drey ersten begriff 23|000|000| die ist 284. deren Cubum 22909304. von gemelten dreyen begriffen ziehe ab / bleibt per resto 90696. zu^[20] diesem rest thue drey circuln / weil vorhin drey begriff von der auffgab abgeschnitten worden: werden 90696000. Ferner gemelte wurtzel 284. triplier / vnd das triplat 852. multiplicier durch eben selbe wurtzel 284. das product 241968. ist der Theiler / mit deme dividier erstgemelte zahl 90696000. den Quotienten 375. thue zu vorgefundener wurtzel 284. werden 284375. welchs ist die nahene wurtzel der auffgebenen surdischen zahl.

Cubic Tafel.

	0	100	200	300
0	0	1000000	8000000	27000000
1	1	1030301	8120601	27270901
2	8	1061208	8242408	27543608
3	27	1092727	8365427	27818127
4	64	1124864	8489664	28094464
5	125	1157625	8615125	28372625
6	216	1191016	8741816	28652616
7	343	1225043	8869743	28934443
8	512	1259712	8998912	29218112
9	729	1295029	9129329	29503629
10	1000	1331000	9261000	29791000
11	1331	1367631	9393931	30080231
12	1728	1404928	9528128	30371328
13	2197	1442897	9663597	30664297
14	2744	1481544	9800344	30956144
15	3375	1520875	9938375	31255875
16	4096	1560896	10077696	31554496
17	4913	1601613	10218313	31855013
18	5832	1643032	10360232	32157432
19	6859	1685159	10503459	32461759
20	8000	1758000	10648000	32768000
21	9261	1771561	10793861	33076161
22	10648	1815848	10941048	33386248
23	12167	1860867	11089567	33698267
24	13824	1906624	11239424	34012224
25	15625	1953125	11390625	34328125
26	17576	2000376	11543176	34645976
27	19683	2048383	11697083	34965783
28	21952	2097152	11852352	35287552
29	24389	2146689	12008989	35611289
30	27000	2197000	12167000	35937000
31	29791	2248091	12326391	36264691
32	32768	2299968	12487168	36594368
33	35937	2352637	12649337	36926037

WS: Diese Seite zeigt die erste Tafel der Kubikzahlen als Beispiel, der Rest wurde nicht transkribiert.

Anmerkungen (Wikisource)

1. Georg Friedrich (1573–1638), Markgraf von Baden-Durlach (vgl. ADB und Wikipedia).
2. Bernegger war Professor für Geschichte.
3. Scharfe Kriter, nach Zoilos von Amphipolis.
4. Peter Crüger (1580–1639), Professor der Mathematik zu Danzig (vgl. ADB und Wikipedia).
5. Amanuensis, ein Schreibgehilfe, Sekretär.
6. Dreisatz
7. Vorlage: Semitirculus
8. siehe Petrus Ramus (1515–1572).
9. Vorlage: 27.
10. Vorlage: arcnm
11. Vorlage: C.
12. Vorlage: vod
13. Vorlage: 1738.
14. Beluarda (poln.) Bastion, vgl. Wiktionary.
15. Vorlage: ${\tfrac {55375108}{1000000}}.$
16. Vorlage: nehnere
17. Vorlage: nntz
18. Vorlage: anß
19. Vorlage: ꝰ (U+A770 Modifier Letter Us)
20. Vorlage: zn