Commentariolus
Bekanntlich entdeckte der durch seine Coppernicus-Forschungen verdiente Professor Maximilian Curtze im Jahre 1873 in der K. K. Hofbibliothek zu Wien ein lateinisches Manuskript mit obiger Aufschrift. Dasselbe wurde in dem ersten Hefte der Mitteilungen des „Coppernicus-Vereins für Wissenschaft und Kunst zu Thorn“ im Jahre 1878 veröffentlicht.
Es handelt sich offenbar um einen Abriß der in dem Hauptwerke (De revolutionibus orbium coelestium) niedergelegten Lehren des „Altmeisters der neuen Astronomie“[1]. Zwar rührt die Handschrift nicht von Coppernicus selbst her, doch ist sie offenbar eine wenn auch zum Teil mangelhafte Abschrift einer von ihm selbst verfaßten kurzen Darlegung seines neuen Weltsystems[2]. Leider fehlte unter den 10 Quartblättern des Wiener Exemplars ein ganzes Blatt, wodurch in dem Kapitel „Ueber den Mond“ [360] (De luna) eine empfindliche Lücke entstand. Diese wurde glücklicherweise durch einen zweiten ähnlichen im Jahre 1878 in der Bibliothek der Stockholmer Sternwarte gemachten Fund ausgefüllt.
Der dort befindlichen, aus dem Besitz von Hevel stammenden Baseler Ausgabe des Coppernicanischen Hauptwerkes ist eine ähnliche Abschrift des „Commentariolus“ angebunden. Der Vergleich beider Manuskripte ermöglichte eine hinreichend genau gestellte Herausgabe der genannten Abhandlung, wie wir sie in der Urkundensammlung von L. Prowe vor uns haben.[3] Dieselbe dient uns als Vorlage bei der folgenden Uebersetzung.
Die Schrift ist nicht, wie man vermuten könnte, eine populär gehaltene Darlegung des coppernicanischen Systems[4]. Das Verständnis derselben setzt gewisse fachmännische Kenntnisse voraus, wie sie selbst bei Gebildeten im weiteren Sinne des Wortes, nicht immer anzutreffen sind. Es handelt sich offenbar um eine für astronomisch geschulte Freunde bestimmte Einführung in die Hauptlehren des noch unveröffentlichten Hauptwerks. Demnach glauben wir den Lesern dieser Zeitschrift einen Dienst zu erweisen, wenn wir das wertvolle, einst in Ermland verfaßte und von da weiter verbreitete Schriftchen durch Uebertragung ins Deutsche und durch Beifügung einiger Erklärungen dem Verständnis weiterer Kreise näher zu rücken suchen.
Bei der möglichst treuen Uebersetzung haben wir es uns dennoch gestattet, nicht so sehr die einzelnen Worte und Satzgefüge, als vielmehr den in ihnen enthaltenen coppernicanischen Gedanken klar wiederzugeben.
Coppernicus lag nichts ferner, als sein System als bloße Rechenhypothese zu empfehlen[5]; er vermeidet sogar mit sichtlicher Sorgfalt den Namen Hypothese, woraus wir wohl den Schluß ziehen dürfen, daß die Ueberschrift des Commentariolus, wie wir sie an die Spitze dieses Artikels gesetzt haben, nicht aus seiner [361] Feder stammt. Ob der von ihm verfaßte Urtext oder sonstige Exemplare von Abschriften noch vorhanden sind, darüber lassen sich einstweilen mir Vermutungen aussprechen. Jedenfalls verdient die Wichtigkeit solcher oder ähnlicher Funde die Aufmerksamkeit der emsigen Forscher in den verschiedenen Bibliotheken des Inn- und Auslandes.
In den Anmerkungen haben wir, wo eine kurze Erklärung nicht auszureichen schien, auf die betreffenden Abschnitte des Hauptwerkes, das ja bereits in deutschem Gewande vorliegt, verwiesen.
Unsere Vorfahren haben, wie ich sehe, eine Menge von Himmelsbahnen angenommen, und zwar aus dem Grunde, um den scheinbaren Bewegungen der Gestirne ihre Regelmäßigkeit zu wahren. Es schien ihnen mit der Natur eines Himmelskörpers durchaus unverträglich, daß derselbe keine vollkommen abgerundete Bahn mit stets gleichförmiger Bewegung beschreiben sollte. Es kann ja wirklich, wie sie fanden, durch die Zusammenstellung und Gesamtwirkung von regelmäßigen Bewegungen ein ungleichmäßiges Fortschreiten nach irgend einem Punkte hin zu stande kommen.[7]
Calippus und Eudoxus haben sich vergebens abgemüht, dies mittels conzentrischer Sphären[8] zu bewerkstelligen, welche nicht blos den siderischen Umlauf der Wandelsterne, sondern auch deren scheinbares Auf- und Absteigen[9] erklären sollten; ein Ding der Unmöglichkeit bei gemeinsamem Mittelpunkt. Man gab daher der Erklärungsweise, wonach dies mittels exzentrischer und epicyklischer Kreise dargestellt wurde, den Vorzug; ja diese fand schließlich die Zustimmung der meisten Gelehrten.[10]
[362] Allein selbst diese Ansicht und all das, was uns von Ptolemäus und vielen anderen darüber berichtet wird, schien trotz des Stimmens der Rechnungen[11] nicht geringen Schwierigkeiten unterworfen. Die bisherigen Kreise genügten nicht, es sei denn man ersinne noch gewisse ausgleichende Kreislinien, um es erklärlich zu machen, daß ein Gestirn weder in seinem Tragkreise, noch auch vom Mittelpunkte aus eine stets gleichförmige Bewegung zeige. So schien also auch diese Betrachtungsweise weder hinreichend abgeschlossen, noch konnte sie den Verstand vollkommen befriedigen.
Während ich nun hierüber nachdachte, kam mir oft der Gedanke, es müsse sich doch eine bessere Zusammenstellung von Kreisen finden lassen, welche bei aller gleichförmigen Bewegung, wie sie die Natur einer vollkommenen Bewegung verlangt,[12], doch zugleich die scheinbaren Verschiedenheiten erkläre. Dabei stellte ich mir die gewiß nicht leichte, ja fast unmögliche Aufgabe, dies schließlich durch wenigere und passendere Annahmen als die bisherigen zu bewerkstelligen, falls man mir nur einige Annahmen einräume, welche ich als sogenannte Grundsätze hiermit folgen lasse:[13]
Es gibt keinen gemeinschaftlichen Mittelpunkt sämtlicher Himmelsbahnen.[14]
[363]
Der Erdmittelpunkt ist nicht das Zentrum des Weltalls, sondern nur der Schwerkraft und der Mondbahn.[15]
Alle Bahnen lagern sich um die Sonne; bei ihr inmitten aller befindet sich die Mitte des Weltsystems.[16]
Vergleicht man die Entfernung von Erde und Sonne mit jener der Fixsterne, so ist das Verhältnis kleiner als das des Erdradius zur Sonnenentfernung; letztere ist mithin im Vergleich zu jener unmerklich klein.[17]
Die scheinbaren Bewegungen des Fixsternhimmels sind nichts als Erdbewegungen. Die Erde dreht sich nämlich mitsamt ihrer nächsten Umgebung täglich um ihre festen Angelpunkte; der Sternhimmel bis zu seinen äußersten Grenzen bleibt dabei unbeweglich.[18]
Alle scheinbaren Bewegungen der Sonne haben ihren Grund nicht in ihr, sondern in den Bahnbewegungen der Erde; diese nämlich kreist nach Art eines Wandelsternes um die Sonne und führt dabei mehr als eine Bewegung aus.[19]
Die scheinbaren Rückläufe und das Fortschreiten der Wandelsterne finden nicht in Wirklichkeit statt, sondern erklären sich durch die Bewegungen der Erde. Die Erdbewegung allein genügt also zur Erklärung der scheinbar so verschiedenen Bewegungen am Himmel.[20]
[364] Dies vorausgeschickt will ich es nunmehr versuchen, kurz auseinanderzusetzen, wie trefflich sich die Gleichförmigkeit der Bewegungen wahren läßt. Dabei schien es mir angezeigt, hier der Kürze halber die mathematischen Beweise zu übergehen. Diese sind einem größeren Werke vorbehalten. Die Größen der Bahnhalbmesser sollen jedoch hier bei der Erklärung der verschiedenen Kreise angegeben werden; mathematisch gebildete Leser werden dann leicht einsehen, wie bei dieser Zusammenstellung von Kreisbahnen Rechnung und Beobachtungen vorzüglich übereinstimmen.
Zugleich wird die Erklärung der verschiedenen Kreise den besten Beweis liefern, daß ich keineswegs in leichtfertiger Weise nach Art der Pythagoreer der Erde eine Bewegung zugeschrieben habe.[21] Alles was die Physiker auf den äußeren Schein gestützt, für die Unbeweglichkeit der Erde vorbringen, erweist sich hier zumal als nicht stichhaltig, da ich desselben Augenscheins wegen die Erdbewegung annehme.[22]
Die Bahnen der Himmelskörper umschließen sich folgendermaßen. Zu oberst befindet sich das alles faßlich und räumlich umgebende, unbewegliche Gewölbe der Fixsterne; darunter befindet sich zunächst Saturn, dann Jupiter, darauf Mars; dann folgt unsere Erdbahn; hierauf die Bahn der Venus und endlich die des Merkur. Die Mondbahn umgiebt die Erde und wird mit dieser wie auf einem Epicykel (Nebenkreise) herumgeführt. In derselben Reihenfolge übertrifft ein Wandelstern den andern an Schnelligkeit der Fortbewegung; je nachdem die einzelnen größere oder kleinere Bahnen zu durchmessen haben. So kehren Saturn nach dreißig, Jupiter nach zwölf, Mars nach drei, die Erde nach einem Jahre [365] zum gleichen Punkte ihrer Bahn zurück. Venus vollendet einen Umlauf in 9 Monaten, Merkur in 3 Monaten.
Die Erde hat eine dreifache Bewegung. Zunächst durchläuft sie alljährlich in ihrem Kreislauf um die Sonne der Reihe nach die einzelnen Sternbilder der Ekliptik.[25] Dabei beschreibt sie um einen [366] Mittelpunkt, der 1/25 Bahnhalbmesser vom Sonnenzentrum entfernt ist, in gleichen Zeiten gleiche Bogen. Da nun genannter Halbmesser im Vergleich zur Ausdehnung des Himmelsgewölbes verschwindend klein ist, so folgt hieraus, daß die Sonne sich um die Erde zu bewegen, diese im Mittelpunkt des Weltalls zu ruhen scheint; obschon die Ursache der Erscheinung nicht in einer Bewegung der Sonne, sondern in der Erdbewegung ihre Erklärung findet; befindet sich beispielsweise die Erde im Sternbilde des Steinbocks,[26] so erblickt man die Sonne im gegenüberliegenden Bilde des Krebses, und so fort. Dabei wird die Bewegung der Sonne, wie gesagt, je nach ihrer Entfernung vom Mittelpunkte (der Bewegung) ungleichförmig erscheinen.[27] Der Unterschied kann einen größten Wert von 21/6 Grad erreichen. Von diesem Zentrum liegt die Sonne in der Richtung des hellen Sterns im Kopfe der Zwillinge etwa 10 Grad gegen Westen ein für alle mal entfernt.[28] Dann also scheint die Sonne in ihrer größten Erdferne, wenn die Erde jenem Orte gegenübersteht, indem das Bahnzentrum zwischen beiden liegt; dabei führt die Erde den Mond und alles, was innerhalb der Mondbahn sich befindet,[29] auf ihrer Bahn mit sich.
Eine zweite Bewegung der Erde ist die ihr vor allem zukommende Drehung um ihre Achse,[30] wodurch sie sich der Reihenfolge der Tierzeichen folgend nach Osten hin dreht und wodurch das ganze Weltall einen gewaltigen Umschwung zu vollführen scheint. Diese Drehung macht die Erde zugleich mit den sie bedeckenden Wassermassen sowie mit den näheren Luftschichten.[31]
[367] Eine dritte Bewegung ist die der Abweichung.[32] Die Achse der täglichen Umdrehung hat nämlich nicht allenthalben den gleichen Abstand von der Bahnachse[33], sondern macht mit ihr nach einem gewissen Punkte der Bahn hin einen Winkel, welcher für unser Jahrhundert nahezu 23 und einen halben Grad erreicht. Während somit der Erdmittelpunkt stets in der Ebene der Ekliptik, d. h. in der großen Bahnlinie bleibt, beschreiben die beiden Pole der Erdachse bei stets gleichbleibendem Abstand kleine Kreise um die Pole der Ekliptik. Auch diese Bewegung hat ihre jährliche mit der großen Umlaufszeit[34] nahe übereinstimmende Periode. Die Achse der Hauptbahn hingehen behauptet stets unveränderlich die gleiche Richtung innerhalb des Himmelsgewölbes nach jenen sogenannten Polen der Ekliptik hin. Die Bewegung der Abweichung in ihrer Zusammenwirkung mit der jährlichen Fortbewegung würde die Pole der täglichen Umdrehung immer in derselben Himmelsgegend festhalten, wenn die Perioden beider genau dieselben wären. Nun hat man aber durch Beobachtungen, die sich über lange Zeiträume erstrecken, herausgefunden, daß diese Stellung der Erde[35] bezüglich des Sternhimmels veränderlich ist; es sind daher gar manche der Ansicht, der Sternenhimmel selbst führe nach einem noch wenig bekannten Gesetze verschiedende Eigenbewegungen aus.[36] Die Beweglichkeit [368] der Erde bietet die Möglichkeit, all diese Erscheinungen auf eine weniger auffallende Weise zu erklären. Was dabei den Polen der Erdachse ihre Richtung gebe[37], das brauche ich nicht auseinanderzusetzen. Uebrigens sehen wir ja im Kleinen, wie ein magnetisirtes Stäbchen sich stets nach derselben Himmelsgegend richtet.[38] Im allgemeinen gab man jener Erklärung den Vorzug, wonach eine besondere Sphäre die Pole mit sich fortbewegt; eine solche müßte zweifelsohne innerhalb der Mondbahn liegen.[39]
Da die Aequinoctialpunkte wie die übrigen Angelpunkte des Weltalls manchen Aenderungen unterworfen sind, so begeht man einen Irrtum, falls man von ihnen die Jahreslänge ableiten will. Diese hat sich denn auch in der That nach den vielen in verschiedenen Zeitperioden angestellten Beobachtungen als eine verschiedene herausgestellt. Nach Hipparch betrug sie 3651/4 Tage, nach dem Chaldäer Albategnius zählt sie 365 Tage, 5 Stunden, 46 Minuten, d. h. 133/5 Minuten weniger als die von Ptolemäus aufgestellte. Der Astronom von Sevilla hingegen macht das Jahr um den 20. Teil einer Stunde länger, indem er ihm 365 Tage, 5 Stunden und 49 Minuten gibt.[41]
[369] Damit man nun nicht etwa glaube, diese Verschiedenheit Beobachtungsfehlern zuschreiben zu können,[42] so beachte man wohl, daß dieselbe in der Verschiebung der Aequinoctialpunkte ihre jedesmalige Erklärung findet. Da nämlich diese Cardinalpunkte, wie man zu Ptolemäus Zeiten entdeckte, in je einem Jahrhundert um einen Grad fortrückten, so hatte das Jahr damals wirklich die von Ptolemäus ihm zuerkannte Länge. Da sie jedoch in den folgenden Jahrhunderten eine größere Beweglichkeit in retrogradem Sinne entwickelten, so wurde das Jahr um so kürzer, je mehr die Cardinalpunkte sich verschoben. Denn durch ihr schnelleres Entgegenkommen machten sie dem Jahreslaufe ein schnelleres Ende.[43] Es wäre daher richtiger, die Zählung der Jahreslänge auf die Fixsterne zu beziehen. Ich bezog so das Jahr auf den Stern Spica in der Jungfrau und fand die von den alten Aegyptern bereits ermittelte Länge von 365 Tagen, 6 und nahezu 1/6 Stunden.[44] Dieselbe Regel sollte man bei den übrigen Wandelsternen befolgen. Das zeigen uns die Lage ihrer Apsiden[45], wie überhaupt ihre Bewegungsgesetze, ja der ganze Sternhimmel, auf unzweifelhafte Weise.
[370]
Der Mond hat, wie bereits angedeutet wurde, allem Anscheine nach eine vierfache Bewegung. Zunächst beschreibt er nämlich auf seinem Tragkreise [G. C. H.], der Reihenfolge der Thierzeichen[47] folgend, einen monatlichen Umlauf um den Mittelpunkt der Erde [D]. Dieser Kreis trägt aber einen sogenannten Epicykel [AHBG] erster Ungleichheit oder erster Ordnung; wir nennen ihn einfach den ersten, den Haupt- oder Jahres-Epicykel. Letzter dreht sich in umgekehrtem Sinne[48] in etwas mehr als einem Monate; dabei führt er auf seiner Außenseite [A] einen ferneren Epicykel [EKFI] mit sich. Dieser endlich trägt den [371] Mond [E] in neuerdings umgekehrter Richtung[49] allmonatlich je zweimal im Kreise herum. Es falle nun der Mittelpunkt [C] des Hauptepicykels in die Richtung der Verbindungslinie der Erde und ihres Bahnzentrums d. h. in die eines Durchmessers der Erdbahn, wie dies bekanntlich zur Zeit des Neu- und Vollmondes geschieht, alsdann steht der Mond [in E] dem Zentrum [C] des Hauptepicykels am nächsten; zur Zeit der mittleren Quadraturen hingegen wird er von demselben [gleich F] am weitesten abstehen.[50]
[372] Der Durchmesser des Hauptepicykels beträgt 1/10 des Radius seines Deferenten, doch ist noch 1/15 dem Teile beizufügen. Derselbe Durchmesser enthalt 5–1/4 mal den Radius des kleineren Epicykels.[51] In Folge dessen hat es den Anschein, als ob der Mond bald schneller bald langsamer auf- und absteige; und zwar bringt seine Bewegung auf dem kleineren Epicykel eine doppelte Unregelmäßigkeit zu stande. Zunächst nämlich scheint er den Hauptepicykel ungleichmäßig zu durchlaufen, wobei die größte Abweichung einen Bogen von 171/4 Grad erreicht; um einen entsprechenden Wert oder Abstand, bestimmt durch den Halbmesser des kleineren Epicykels, rückt er dem Mittelpunkte des größeren bald näher, bald ferner. Da somit der Mond um das Zentrum des Hauptepicykels ungleiche Kreisbogen durchläuft, so erleidet dadurch die erste Ungleichheit manche Veränderung. So kommt es, daß zur Zeit der auf die Sonne bezogenen Konjunktionen und Oppositionen diese Ungleichheit 4 Grade und 56 Minuten nicht überschreitet, während sie zur Zeit der Quadraturen 6 Grade und 36 Minuten erreicht. Die, welche [373] vermeinten, diese Ungleichheit mittels eines exzentrischen Kreises erklären zu können, fielen dabei in zwei offenbare Irrtümer. Daraus würde nämlich mit mathematischer Gewißheit folgen, daß der Mond zur Zeit der Quadraturen, wo er sich an der Innenseite des Epicykels befindet, vier mal größer erscheinen müßte (falls seine ganze Scheibe sichtbar wäre) als zur Zeit des Neu- oder Vollmondes; es sei denn, man behauptete thörichterweise ein wirkliches Wachsen und Abnehmen der Mondkugel. Es müßte auch wegen der im Verhältnis zur Entfernung großen Erde der scheinbare Unterschied in der Größe noch viel auffallender sein. Betrachtet man jedoch die Sache aufmerksam, so wird man finden, daß der Größenunterschied zur Zeit der Quadraturen und zur Zeit des Neu- und Vollmondes ein ungemein geringer ist; somit dürfte unsere Anschauungsweise nicht leicht in Zweifel zu ziehen sein. Bei den erwähnten drei Bewegungen in die Länge hat der Mond noch eine Bewegung in die Breite. Die Achsen der Epicykel liegen parallel des Bahnachse, weshalb der Mond aus seiner Bahnebene nicht heraustritt.
Diese Achse der Bahn ist jedoch gegen die Achse des größten Kreises der Ekliptik geneigt, weshalb der Mond von der Ebene der letzteren abweicht. Das Maß der Abweichung beträgt 5 Bogengrade; die Pole der Bahnebene beschreiben um jene der Ekliptik bei stets gleichbleibender Entfernung einen Kreis, ähnlich wie dies bei der Abweichung[52] erörtert ward. Hier hingegen findet die Bewegung gegen die Reihenfolge der Thierzeichen und viel langsammer statt, so daß zu einem vollständigen Umlauf 19 Jahre erforderlich sind. Nach der gewöhnlichen Anschauung geschieht dies, indem eine größere Sphäre in der die Pole der Bahnachse lagern, diese mit sich herumführt.[53] So dürfte die Zusammenstellung der Mondbewegungen sich erklären.[54]
[374]
Saturn, Jupiter und Mars führen ähnliche Bewegungen aus; indem ihre Bahnen die oben besprochene große (Erd-) Bahn vollständig umschließen, drehen sie sich um das Zentrum der letzteren nach der Reihenfolge der Thierzeichen. Saturn vollführt seinen Rundgang in 30 Jahren, Jupiter in zwölf, Mars in 29 Monaten; gleichsam als ob die Größe der Bahn die Umläufe verzögere. Nehmen wir zum Halbmesser der Erdbahn 25 Teile, so wird jener der Marsbahn 30, der des Jupiter 1301/5, der des Saturn 2361/6 Teile in Anspruch nehmen. Dabei messe ich die Länge des Halbmessers vom Mittelpunkt der Bahn bis zu dem des Hauptepicykels. Es hat nämlich jeder Planet zwei Epicykel, von denen, wie wir dies beim Monde sahen, der eine den anderen trägt; jedoch ist die Art der Bewegung verschieden. Der Hauptepicykel hat eine der Bahnrichtung entgegengesetzte Bewegung, wobei die Umlaufszeiten die gleichen sind; der zweite hingegen vollführt gegen die Bewegung des ersten einen doppelten Umschwung. Befindet er sich deshalb in größter oder nächster Entfernung vom Zentrum der Hauptbahn, so ist der Planet dem Mittelpunkte des Hauptepicykels am nächsten, während er zur Zeit der mittleren Quadraturen am weitesten von demselben absteht.[56] Aus der Zusammenstellung dieser Bewegungen der Hauptbahn[57] der Epicykel mit ihren gleichförmigen Umläufen geht nun hervor, daß diese Entfernungen und Näherungen in durchaus bestimmten Himmelsgegenden stattfinden.
Im übrigen gelten überall durchaus feste Gesetze der Bewegung, wobei die Apsiden unverändert ihre Richtung beibehalten: bei Saturn liegen dieselben in der Richtung jenes Sternes, der sich im Ellbogen des Schützen befindet; bei Jupiter 8 Grad nach [375] dem Sterne, welcher vom Schweife des Löwen seinen Namen hat; bei Mars gehen sie 6 Grad dem Herzen des Löwen voraus.
Die Größen der Epicykel sind folgende. Beim Saturn umfaßt der Halbmesser des ersten 1941/60 jener Teile, deren wir 25 für den Halbmesser der Erdbahn ansetzten.[58] Der zweite Epicykel hat einen Radius von 634/60 Teilen. Beim Jupiter hat der erste Epicykel einen Halbmesser von 106/60, der des zweiten mißt 322/60 Teile. Beim Mars gehen auf den ersten 534/60, auf den zweiten 51/60 Teile.[59] So ist allenthalben zunächst der Halbmesser des ersten Epicykels 3mal so groß wie der des zweiten.[60] Die Ungleichheit, welche die Bewegung der Epicykel bezüglich der Hauptbahn hervorbringt, hat man die erste (Ungleichheit) genannt; dieselbe zeigt sich stets, wie gesagt, innerhalb gewisser Grenzen am Himmelsgewölbe. Es giebt nämlich noch eine andere Ungleichheit, durch welche das Gestirn zuweilen rückläufig wird, öfter still zu stehen scheint; diese Erscheinungen rühren nicht von wirklichen Ortsveränderungen des Gestirns her, sondern von der verschiedenen Stellung der Erde in ihrer Bahn[61]. Indem nämlich die Erde durch ihre größere Schnelligkeit dem Planeten vorauseilt, trifft die Visirlinie das Himmelsgewölbe in einem zurückliegenden Punkte. [376] Dies geschieht namentlich, wenn der Planet der Erde nahe steht, wenn wir uns nämlich zwischen der Sonne und dem Planeten befinden, dieser also zur Zeit des Sonnenunterganges aufgeht. Zur Zeit hingegen, wo der Planet Abends untergeht, oder zur Morgenzeit aufgeht, eilt die Visirlinie voraus. Geschieht endlich die Bewegung in der Richtung und bei gleichmäßiger Verschiebung der Sehlinie, so scheint der Planet stille zu stehen, indem die verschiedenen entgegengesetzten Bewegungen sich gegenseitig aufheben. Es findet dies meist beim Gedrittschein der Sonne statt. Bei all diesen Erscheinungen ist die Ungleichheit um so größer, je näher das Gestirn der Erdbahn; somit ist sie kleiner beim Saturn, als beim Jupiter; am größten zeigt sie sich beim Mars, je nach dem Verhältnis des Halbmessers der Erdbahn zu der Planetenbahn. Sie erreicht bei jedem einzelnen ihren größten Wert, wenn die Sehlinie eine Tangente zur Erdbahn bildet. So dürfte der Wandel dieser drei Sterne erklärt sein. Doch machen sie auch noch eine zweifache Bewegung in Breite;[62] denn die Kreise der Epicykel liegen zwar in der Ebene der Hauptbahn, jedoch nicht in der der Ekliptik. Ihre Achsen machen vielmehr mit der der Ekliptik einen Winkel; dabei bewegen sie sich jedoch nicht, wie wir dies beim Monde sahen, um letztere herum, sondern behalten stets dieselbe Richtung am Himmel bei. Somit behalten auch die Durchschnittslinien dieser Ebenen, die sogenannten Knotenlinien, ein für alle mal dieselbe Lage. Für Saturn liegt der aufsteigende Knoten 81/2 Grad[63] nach dem östlichen Sterne am Haupte der Zwillinge; für Jupiter 4 Grad vor dem genannten Stern; der Knoten der Marsbahn liegt 61/2 Grade vor den Plejaden.[64]
An diesen Oertern, so wie an den diametral gegenüberliegenden ist also die Breite des Planeten gleich Null. Sie erreicht ihren sehr veränderlichen großen Wert bei einem Längenunterschied von 90° von jenen Punkten. Die Neigung der verschiedenen Achsen und Kreise haben nämlich in jenen Knoten gewissermaßen ihre [377] Angelpunkte;[65] sie scheinen am größten, wenn der Planet der Erde am nächsten, d. h. zur Zeit seines Abendaufganges.[66] Dann erreicht nämlich die Neigung der Bahnachse bei Saturn 22/3°, bei Jupiter 2°–1/3°, bei Mars 11/6°. Zur Zeit des Abenduntergangs hingegen und des Frühaufganges,[67] wo der Planet sich in seiner Erdferne befindet, wird die Neigung bei Saturn und Jupiter um 1/5° kleiner, bei Mars um 12/3°. Dieser Unterschied zeigt sich besonders bei größeren Breiten; indem er nämlich mit der Breite ab- und zunimmt, scheint er um so geringer, je näher der Planet seinem Knoten. Dazu kommt, daß auch die Bewegung der Erde in (der Ekliptik) ihrer Bahn eine scheinbare Aenderung in der Breite verursacht, indem sie nämlich durch ihre Annäherungen und Entfernungen die Breitenwinkel vergrößert oder verkleinert, wie dies ja mathematisch sein muß, da diese Schwankung sich in gerader Linie vollzieht. Es kann allerdings geschehen, daß diese Bewegung sich aus den Bewegungen zweier Sphären herausbilde.[68] Sind diese nämlich conzentrisch, so führt die eine die von dem eigenen abstehenden Pole der andern herum; dabei mag die innere die Pole des Tragkreises des Epicykel gegen die Bewegung der äußeren mit verdoppelter Geschwindigkeit zurückdrehen; dabei würden diese Pole von denen der unmittelbar höheren Sphäre so weit abstehen, als diese wiederum von denen der höchsten. Dies mag genügen über die außerhalb der Erde (Erdbahn) liegenden Bahnen der Planeten Saturn, Jupiter und Mars.
[378]
Es erübrigt noch die Bewegungen zu betrachten, welche sich innerhalb der Erdbahn vollziehen, nämlich die der Planeten Venus und Merkur. Die Venus zeigt eine den oben erwähnten durchaus ähnliche Zusammenstellung von Kreisen, doch ist die Art der Bewegungen eine verschiedene. Auf der Hauptbahn wie beim Hauptepicykel vollzieht sich der Umlauf, wie gesagt, in neun Monaten; durch die zusammengesetzte Bewegung kommt ein kleinerer Epicykel immer wieder in dieselbe relative Stellung am Himmel, indem seine obere Apsis stets mit der Sonnenrichtung zusammenfällt. Die Umlaufszeit dieses kleineren Epicykels ist verschieden von der der oben genannten Kreise; so entsteht längst der Ekliptik eine ungleichförmige Bewegung. Vollführen jene einen Umlauf, so führt der kleinere einen doppelten aus; hierdurch kommt der Planet dem Zentrum seines Hauptepicykels am nächsten, wenn die Erde sich in der Richtung des durch die Apsiden gelegten Durchmesser befindet; bei den querliegenden Quadranten scheint er am weitesten davon entfernt, ganz ähnlich, wie beim Monde der kleinere Epicykel sich stets nach der Sonne richtet. Das Verhältnis der Halbmesser von Erd- und Venusbahn ist 25 : 18; der Hauptepicykel umfaßt 2/3, der kleinere 1/4 Teile.[70]
Auch die Venus wird zuweilen rückfällig, besonders bei ihrer Erdnähe, ähnlich wie wir oben sahen, aber in anderem Sinne. Dort nämlich war dies eine Folge der schnelleren Erdbewegung, hier der langsameren; dort befand sich die Erdbahn innerhalb der übrigen Bahnen, hier sehen wir sie außerhalb. Aus letzterem Grunde kann der Planet (Venus) auch nie in Opposition mit der Sonne kommen, da die Erde unmöglich zwischen beide treten kann; hat er eine gewisse Entfernung von der Sonne erreicht, wo die vom Erdmittelpunkt nach ihm gezogene Linie eine Tangente seiner Bahn wird, so kehrt er um. Von der Erde gesehen entfernt er sich dabei nie über einen Winkelabstand von 48 Grad von der Sonne [379] auf der einen wie auf der anderen Seite. Dies sind die Bewegungen in Länge; jedoch auch in Breite sehen wir eine Verschiebung aus doppeltem Grunde. Es hat nämlich auch die Venusbahn eine Achsenneigung von 2 Grad[71]; der aufsteigende Knoten fällt mit der Apsis zusammen. Die aus dieser Neigung folgende Ablenkung, obschon in sich ein und dieselbe, zeigt sich auf doppelte Weise.[72] Befindet sich nämlich die Erde in einem der Knoten der Venusbahn, so erblickt man den Planeten quer höher oder tiefer,[73] es sind die sogenannten „Reflexe“; in den Quadraturen hingegen sieht man die sogenannten Abweichungen, entsprechend den natürlichen Neigungen. Bei allen übrigen Stellungen vermengen sich die beiden Breitenunterschiede; bald erscheint der eine, bald der andere größer, und je nachdem sie im gleichen oder entgegengesetzten Sinne auftreten, häufen sie sich oder heben sich gegenseitig auf. Die so beschriebene Schiefe der Bahnachse erleidet jedoch eine Schwankung, nicht wie die obigen Planeten um ihre Knotenpunkte, sondern um gewisse andere verschiebbare Punkte, die in Bezug auf den Planeten einen jährlichen Umlauf vollführen, und zwar so, daß der Ausschlag der Schwankung des Planeten am größten ist, wenn die Erde sich gegenüber der Apsis der Venusbahn befindet; dabei kann der Planet selbst an einem beliebigen Punkte seiner Bahn stehen.[74] So erklärt es sich, daß selbst wenn der letztere gleichzeitig in der Apsis oder dem gegenüberliegenden Punkte, also in seinen Knotenpunkten steht, dennoch seine Breite nicht gleich Null ist. Von hier an bis die Erde sich um einen Quadranten von genanntem Orte entfernt hat, vermindert sich diese Ablenkung, um schließlich spurlos zu verschwinden, zumal wenn [380] der Punkt größter Schwankung vom Planeten eben so weit absteht.[75] Indem nämlich der Planet sich allmählich entfernt und die Erde aus der Apsis hinaustritt, dauert die anfangs von Nord nach Süd ablenkende Schwankung fort[76] und bringt das Gestirn nach einem vorher südlich gelegenen Orte. Jetzt aber ist dieser umgekehrt zu einem nördlichen geworden, bis nach Ablauf der Schwankungsperiode die Ablenkung wiederum ein dem obigen vollkommen gleiches Maximum erreicht. Aehnlich ist das Verhalten im übrigen Halbkreise. So kommt es, daß die meist als Schwankung bezeichnete Ablenkung in Breite nie eine südliche wird. Auch hier kann man sich, wie wir dies oben andeuteten, den Vorgang mittels zweier conzentrischer Sphären mit verschiedener Achsenlage vorstellen.
Am wunderlichsten von allen Planetenbahnen ist die des Merkur, dessen Wege schwer zu erforschen, ja nahezu unerforschlich sind. Dazu kommt noch die Schwierigkeit, daß er meist in den Sonnenstrahlen verschwindet und sich nur an wenigen Tagen blicken läßt. Uebrigens läßt auch sein Lauf sich ermitteln, wenn man ihn nur mit tieferem Verständnis studiert. Auch Merkur hat wie die Venus, zwei Epicykel, die sich beide auf seiner Bahn drehen. Wie dort, so vollführt hier der größere seine Umläufe gleichzeitig mit der Hauptbahn, wobei seine Apsis 141/2 Grad dem Sterne Spica in der Jungfrau nachsteht. Der kleinere hingegen vollführt im entgegengesetzten Sinne zwei Umläufe; findet sich daher die Erde bei seiner Bahnapsis oder dem entgegengesetzten Punkte, so steht der Planet vom Zentrum des Hauptepicykels am weitesten [381] entfernt; in den Quadraturen ist er ihm am nächsten. Wir sagten, daß Merkur in 3 Monaten oder 88 Tagen einen Umgang vollendet, wobei der Radius seiner Bahn 92/5 von jenen 25 Theilen umfaßt, die wir dem Radius der Erdbahn zuwiesen. Auf den Hauptepicykel kommen 141/60 Theile, auf den zweiten 1/3 hiervon d. h. ungefähr 34/60.[78] Doch genügen diese Kreise hier nicht wie bei den übrigen Planeten. Befindet sich nämlich die Erde in jenen Gegenden der Apsiden, so scheint der Planet sich viel langsamer zu bewegen, als man nach der Anordnung genannter Kreise erwarten sollte in den Quadraturen hingegen viel schneller.
Da übrigens hiedurch kein weiterer Unterschied in Länge beobachtet wird, so muß dies wohl durch eine gewisse gradlinige Annäherung und Entfernung des Bahnmittelpunktes erklärt werden.[79] Diese kann mittels Drehung zweier kleiner Sphären bewerkstelligt werden, deren Achsen der Bahnachse parallel sind, dabei steht der Mittelpunkt des Hauptepicykels oder seiner ganzen Achse vom Zentrum des unmittelbar ihn tragenden Kreises genau so weit ab, als das Zentrum dieses vom Mittelpunkte des äußersten[80]. Für diesen Abstand hat man das Maaß vom erhalten, wobei die 25 Theile des Erdbahnradius stets die Einheit geben. Darnach macht das entferntere Kreischen einen doppelten Umlauf in einem Jahre, das nähere hingegen in umgekehrter Richtung die doppelte Anzahl, d. h. 4 Umläufe. Auf diese Weise nämlich bringt die zusammengesetzte Bewegung eine gradlinie Bewegung des Epicykelmittelpunktes hervor, wie wir dies bei der Schwankung [382] in Breite andeuteten. So also wird bei Ankunft der Erde auf der Apsidenlinie der Mittelpunkt des Hauptepicykels dem Bahnzentrum am nächsten sein, zur Zeit der Quadraturen hingegen am weitesten davon abstehen. Bei den Mittelstellungen d. h. 45 Grad von diesen entfernt, wird das Zentrum des Hauptepicykels das des kleinen Kreises einholen, beide fallen zusammen. Die Strecke dieser Hin- und Herbewegung mißt 29/60 genannter Teile. So viel über die Bewegungen des Merkur in Länge. In Bezug auf die Breite beobachtet er ein ähnliches Verhalten wie die Venus, jedoch stets im umgekehrten Sinne. Während diese nämlich nach Norden steigt, bewegt er sich südwärts. Seine Bahn weicht von der Ekliptik 7 Grade ab; doch übersteigt die Ablenkung nach Süden nie den zwölften Teil eines Grades. Im übrigen genüge es, um nicht öfter dasselbe zu wiederholen, an das zu erinnern, was wir über die Aenderungen in der Breite bei der Venus gesagt haben.
So haben wir also für Merkur sieben Kreisbewegungen, für Venus fünf, für die Erde drei, für ihren Begleiter den Mond vier, für Mars, Jupiter und Saturn je fünf. So reichen demnach im ganzen 34 Kreise aus, um den ganzen Bau und die Bewegungen des Planetensystems zu erklären.
- ↑ Unter dem Titel „Nikolaus Copernicus, der Altmeister der neueren Astronomie,“ hat der Verfasser dieser Arbeit vor kurzem ein Lebens- und Kulturbild des großen Sternforschers bei Herder in Freiburg (Breisgrau) erscheinen lassen. Oefterer Verweis darauf unter dem Titel M. C. u. s. w. erlaubt ihm in den unten folgenden Erklärungen manches zu kürzen.
- ↑ vgl. M. C. 80.
- ↑ „Nicolaus Coppernicus“ von L. Prowe. – Berlin 1884. II. Band: Urkunden S. 184 ff.
- ↑ „Mathemata mathematicis scribuntur“ war einer der Wahlsprüche des Coppernicus. – Vgl. M. C. 109 u. 150.
- ↑ vgl. M. C. 109 ff.
- ↑ Man übersehe nicht was wir hierüber in der Einleitung gesagt haben.
- ↑ vgl. M. C. 57.
- ↑ Wir glauben so das Wort circulos, welches hier im Gegensatz zu orbes gebraucht ist, wiedergeben zu sollen. Vgl. ebend. S. 59. In seinen Hauptwerken hat Coppernicus diese Systeme nicht weiter erörtert.
- ↑ Zumal eine Annährung und Entfernung ist bei concentrischen Sphären unmöglich.
- ↑ A. a. O. S. 60–66.
- ↑ Es kann hier natürlich nur von einem Stimmen im Sinne einer großen Annäherung die Rede sein.
- ↑ „Ratio absoluti motus poscit.“ – Eine vollkommene Bewegung im Sinne der Alten war nur die gleichförmige Bewegung in einer Kreisbahn. – A. a. O. S. 64. – Vgl. Rev. l. 4. c. 3.
- ↑ Die weitere Ausführung dieser Sätze war natürlich dem Hauptwerk vorbehalten. Wir werden die betreffenden Stellen kurz angeben.
- ↑ Das Wort Mittelpunkt wird hier im streng geometrischen Sinne aufgefaßt. In der That lagern ja auch im Coppernicanischen Systeme die verschiedenen Bahnen exzentrisch um die Sonne. – Wenn daher Prowe (I. 2. 290) übersetzt: „Für alle Himmelskörper und deren Bahnen giebt es nur einen Mittelpunkt,“ so muß er dabei (falls es sich nicht um ein Versehen handelt) eine Verstümmelung des Originaltextes voraussetzen, wozu kein Grund vorliegt. Der Satz scheint gegen die oben erwähnten conzentrischen Sphären des Eudoxus und Kalippus gerichtet. Vgl. M. C. 81 u. 114, ebenso Rev. l. 1. c. 9.
- ↑ Rev. l. 1. c. 7, 8. – l. 4. introductio etc. – Vgl. M. C. 69 und 114.
- ↑ Rev. l. 1. c. 9.
- ↑ Rev. l. 1. c. 6. – M. C. 113.
- ↑ Rev. l. 1. c. 5.
- ↑ Rev. l. 1. c. 9, 11. – Das Wort sidus wird hier und im folgenden durchgängig im Sinne von Wandelstern (Planet) gebraucht, im Gegensatz zu stella „Fixstern.“
- ↑ Rev. l. 5. c. 3. – Vgl. M. C. 77.
- ↑ Es bleibt auch im lateinischen Texte zweideutig, ob die Leichtfertigkeit auf Rechnung Pythagoras zu setzen. In der That stützte sich dessen Ansicht auf leichtfertige mysteriöse Gründe. – M. C. 68.
- ↑ Was uns die Sinne (physiologischen Eindrücke) über die Unbeweglichkeit der Erde sagen, wird im coppernicanischen Systeme durchaus berücksichtigt und gewahrt, ja sogar als Gegenbeweis verwerthet.
- ↑ Rev. l. 1. c. 10. Das betreffende Kapitel des Hauptwerkes trägt ebenfalls die Ueberschrift: „De ordine coelestium orbium.“
- ↑ Rev. l. 1. c. 11. Da diese scheinbaren Bewegungen der Sonne wie oben schon angedeutet wurde, in Wirklichkeit Bewegungen der Erde sind, so hat Coppernicus im Hauptwerke (1. c.) den Titel vorgezogen: „De triplici motu Telluris demonstratio.“ – In der That beginnt ja auch hier der Abschnitt des Commentariolus mit den Worten: „Terra triplici motu circumfertur.“
- ↑ Zur Bezeichnung der „Ekliptik“ wird hier wie im folgenden gewöhnlich der lateinische Ausdruck Orbis magnus angewandt. Wir übersetzen denselben je nach dem Sinne mit Zodiacus, Thierkreis (signifer), Erdbahn oder Sonnenbahn. Bekanntlich durchläuft die Sonne anscheinend alljährlich diesen „größten Himmelskreis;“ in Wirklichkeit ist es die Bahn der Erde, die ihn auf das Himmelsgewölbe einzeichnet.
Auch dürfte es nicht überflüssig sein, hier auf den Unterschied der Bedeutungen aufmerksam zu machen, welche dem lateinischen Worte orbis in der Astronomie beigelegt werden. Bald bezeichnet man damit einfach hin eine Bahn; gewöhnlich sogar eine Kreisbahn. In diesem Sinne kommt das Wort gleich in der ersten Zeile des Commentariolus vor. Dabei kann bald die Bahnlinie, bald die Bahnebene gemeint sein. Oefter bezeichnet man mit orbis eine Hohlkugel. P. Clavius macht geradezu einen Unterschied zwischen Orbis und sphaera (Vollkugel), indem er in seinem Commentar „in sphaeram Joannis De Sacro Bosco“ (Lugduni 1607 p. 19) schreibt: „Hoc namque differt orbis a sphaera, quod haec ad centrum neque tota sit solida, unitaque tantum superficie puta convexa exteriore concludatur, orbis autem non ita, sed duabus finiatur superficiebus; una exteriore et altera interiore, quales sunt omnes caeli.“ Dies macht es uns erklärlich, weshalb in nicht wenigen Exemplaren der editio princeps der Revolutiones die Worte orbium coelestium getilgt sind. So z. B. in den Exemplaren der Vaticanischen und Upsalaer Bibliothek. Ein drittes Exemplar der Bibliothek von Wolfenbüttel hat dazu die Anmerkung: nec ipse (Cop.) addidit „orbium coelostium“ sed alius quispiam. Es lag nämlich Coppernicus nichts ferner als die Ideen der Alten in dieser Hinsicht wieder in Credit zu bringen. – Daß übrigens diese Unterschiede nicht immer gewahrt [366] sind zeigen uns zahlreiche Beispiele. Redet man ja von den Sphären des Eudoxus, der achten Sphäre, vom orbis terrarum u. s. w. Vgl. M. C. S. 57 ff. - ↑ Ganz dasselbe Beispiel findet sich im angeführten Kapitel des Hauptwerkes: „Capricornum centro terrae permeante sol Cancrum videatur pertransire … et sic deinceps.“
- ↑ Vgl. unsere weitere Auseinandersetzung a. a. O. S. 61.
- ↑ In Wirklichkeit ist auch die Stellung dieser sogenannten Apsidenlinie einer Aenderung unterworfen.
- ↑ Darunter ist hier vor allem die Atmosphäre zu verstehen.
- ↑ Rev. l. 1. c. 11 wird diese Bewegung an erster Stelle erwähnt.
- ↑ Es wird dies ausdrücklich hervorgehoben, um große Schwierigkeiten der Alten zu umgehen. Vgl. M. C. 113.
- ↑ Rev. l. 1. c. 11. – Coppernicus suchte durch Einführung dieser dritten Erdbewegung den anscheinend dauernden Parallelismus der Erdachse zu erklären. A. a. O. 119 haben wir uns weiter über diese geistreiche Erklärung verbreitet; ebenso in einem Artikel der „Stimmen aus Maria Laach“ [L. II. 1897, 361 ff.]
- ↑ Mit anderen Worten: Die Drehungsachse der Erde ist nicht der Achse der Ekliptik parallel.
- ↑ „revolutiones compares cum orbe magno;“ man sollte erwarten in orbe magno. Bedenkt man jedoch, daß es bei der Bewegung eines materiellen Punktes auf einer Kreislinie auf dasselbe hinausläuft, ob wir die ganze Linie mit dem auf ihr festgedachten Punkte, oder auf der festgedachten Linie den beweglichen Punkt kreisen lassen, so schwindet alle Schwierigkeit. Coppernicus dachte gewiß nicht an bewegliche materielle Kreise; doch trägt er an manchen Stellen dieser an und für sich gleichgültigen Ausdrucksweise der Alten Rechnung.
- ↑ D. h. der Erdachse.
- ↑ Hiermit werden die Motus octavae sphaerae angedeutet. Vgl. M. C. 79.
- ↑ Wörtlicher heißt es: „Worin die Enden der Erdachse lagern“ quibus autem poli inhaereant; doch giebt die unmittelbar folgende Erklärung der angeführten freieren Uebersetzung den Vorzug.
- ↑ Curtze glaubt in dieser Stelle eine Anspielung auf eine epistola De Magnete des Petrus de Maricourt zu finden. (Mittheilungen des Coppernicus-Vereins I. Heft. S. 9.) Daß Coppernicus den Magneten und speziell die Haupteigenschaften der Magnetnadel kannte, ersehen wir zudem hinreichend aus den Schriften seines Schülers Rheticus. Vgl. Hipler: Die Chorographie des Joachim Rheticus. Dresden 1876. S. 22.
- ↑ Eine Anspielung auf die Sphärentheorie der Alten. Vgl. M. C. 57 ff.
- ↑ Rev. l. 3.
- ↑ Die hier gemachten Angaben finden sich im Hauptwerke etwas genauer angegeben (l. 3. c. 53.) Isidor von Sevilla (Hispalensis) wird dort nicht erwähnt.
- ↑ In der That haben die Beobachtungsfehler der Alten zur Verdunkelung dieser Frage nicht wenig beigetragen. Vgl. M. C. S. 40 ff. u. 121.
- ↑ Die jährliche Präcession der Aequinoctien, deren letzten Grund erst Newton erkannte, wächst wirklich mit der Zeit, aber nur um etwa 6 Sekunden in 1000 Jahren.
- ↑ Auf diese Weise erhält man jedoch nicht mehr den Werth des tropischen, sondern den des siderischen Jahres, d. h. die Zeit welche die Sonne braucht, um nach dem Verlassen eines Fixsterns, der mit ihm in Conjunction steht, wiederum zu ihm zurückzukehren. In neuerer Zeit pflegt man dafür 365,2563582 Tage oder 365 Tage, 6 Stunden, 9 Minuten, 9,35 Sekunden mittlerer Zeit anzusetzen, was mit dem angeführten Näherungswerthe gut stimmt.
- ↑ Apsiden nennt man bekanntlich bei einer Planetenbahn die Endpunkte der Linie, welche durch das Zentrum der Bahn und durch die exzentrisch liegende Sonne gezogen ist. Der Punkt, welcher der Sonne näher liegt, heißt Perihel, der entferntere Aphel. Die Veränderlichkeit dieser Linien war im Allgemeinen zu Coppernicus Zeiten noch wenig bekannt.
- ↑ Dieser Abschnitt wird in dem Hauptwerke (l. 4) ausführlich behandelt. Um dem Leser das Verständnis des hier Gesagten zu erleichtern, fügen wir hier eine Figur bei, deren Erläuterung wir dem Texte einfügen, alles dort

Eingeklammerte findet sich nicht im Commentariolus. Die Figur haben wir der des Hauptwerkes (l. 4. c. 3) angepaßt. Die Bewegungsrichtungen der verschiedenen Kreise sind durch Pfeile angedeutet.
Da Coppernicus die wahre (elliptische) Gestalt der Planetenbahnen noch nicht kannte, mußte er zu diesen von seinen Vorgängern bereits ersonnenen Hilfsmitteln seine Zuflucht nehmen, um den Beobachtungsresultaten gerecht zu werden. Dadurch wurde allerdings die Schönheit und Einfachheit seines heliozentrischen Systems bedeutend in Schatten gestellt. – Vgl. M. C. S. 62 ff.
- ↑ Diese folgen sich in der bekannten Reihenfolge: Widder, Stier, Zwillinge, Krebs, Löwe, Jungfrau, Wage, Skorpion, Schutze, Steinbock, Wassermann, Fische. Die angedeutete Bewegung wird von den Astronomen einfachhin rechtläufige (directe), die umgekehrte rückläufige (retrograde) genannt.
- ↑ D. h. im rückläufigen Sinne.
- ↑ Also rechtläufig.
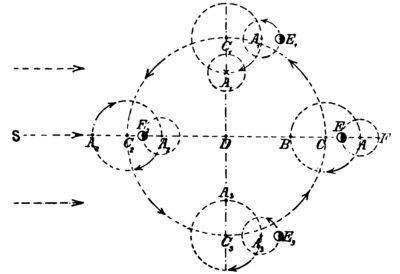
- ↑ Auch das hier Gesagte wird durch eine Figur viel klarer. – D bezeichne das Zentrum der Erde. Die Sonne, die dem Mittelpunkt der Erdbahn nahe steht, sende ihre Strahlen in der Richtung SD; CC1 C2 C3 sei der Hauptepicykel der Mondbahn. Befindet sich der Mond bei C, so hat die Erde Vollmond, bei C2 Neumond; in beiden Fällen fällt der Radius DC, DC2, mit der Richtung SD zusammen. In den Quadraturen C1 und C3, bildet SD mit den Radien DC1 und DC3 einen rechten Winkel. Legen wir nun nach obiger Anweisung um das jedesmalige C den ersten Hauptepicykel, so wird der Punkt A seiner Peripherie sich nach obigen Bewegungsgesetzen bei C in A, bei C1 in A1, bei C2in A2, bei C3 in A3 finden. Das jedesmalige A bilde den Mittelpunkt des zweiten kleineren Epicykels. Auf ihm finden wir den Mond, und zwar in seiner größten Annäherung an das Zentrum des Hauptepicykels in E (bei C) zur Zeit des Vollmondes, in E2 (bei C2) zur Zeit des Neumondes, im E1 (bei C1) zur Zeit dis letzten Viertels, [372] in E3 (bei C3) zur Zeit des ersten Viertels. In den beiden letztgenannten Stellungen steht der Mond also vom Mittelpunkte des Hauptepicykels am weitesten entfernt.
- ↑ Darnach wäre also nach unserer Figur , oder AB : DC = 19 : 180, dies stimmt genau überein mit einer von Coppernicus selbst herrührenden Bemerkung in einem von ihm benutzten Exemplare der Tafeln des Königs Alphons und Regiomontans. Dort schreibt er „Semidiametrus orbis Lunae ad epicyclium a. “. – Also verhält sich DC : AB = 10 : 11/18 = 10 : 19/18 = 180 : 19.
Auch die Angabe der weiteren Verhältnisse, wonach AB = (5–1/4) AF findet dort ihre Bestätigung, indem es heißt „epicyclus a. ad b. 19/4“ also AB : AF = 19 : 4 oder AB = 19/4 AF = (20/4–1/4) AF = (5–1/4) AF. (Vgl. Curtze „Reliquiae Coppernicanae“ p. 30) –
Wir haben diese Verhältnisse der größeren Anschaulichkeit wegen in unserer Figur vernachlässigt; auch sind dieselben im Hauptwerke wie in der Narratio prima geändert.
Statt „una quarta ipsius“ (1/4) heißt es in der Stockholmer Ausgabe una parte ipsius. Der Vergleich mit jener Aufzeichnung berechtigt uns (mit Curtze) die erstere Lesart vorzuziehen, oder besser gesagt, das parte als Schreibfehler anzusehen. - ↑ D. h. bei der Abweichung der Erdachse.
- ↑ M. C. 58 ff.
- ↑ Die Wiener Handschrift sagt: „Tandem igitur videtur haberi Lunae motuum fabrica;“ die Stockholmer: „Talem igitur videtur habere Luna motuum fabricam“ verdient offenbar den Vorzug.
- ↑ Vgl. im Hauptwerk lib. V. cap. 1–15.
- ↑ Vgl. obige Figur (Anmerk. 50).
- ↑ Man kann sich nämlich (vgl. Anm. 34) einen Punkt auf der festen Kreislinie oder auch den ganzen Kreis mit dem auf ihm festliegenden Punkte gedreht denken; die letztere Anschauungsweise kommt der Sphärentheorie der Alten näher.
- ↑ Statt 1941/60 heißt es 19 Teile und 41 Minuten („constat partibus 19 et 41 minutis,“ abgekürzt 19 M. 41), wobei eine Minute den 60. Teil des Hauptteils bedeutet.
- ↑ Auch die hier angeführten Zahlen stimmen mit den anderswo erwähnten gut überein. Auf der in Anm. 51 genannten Bemerkung (vgl. Prowe, N. Cop. II. Urkunden p. 211) heißt es nämlich:
„proportio orbium coelestium ad eccentrotetem 25 partium.“
„Martis semidyametrus orbis 38 fere. Epicyclus. a. 5. M. 341/2.“
„Epicyclus. b. M. 51.“
„Jovis semidyametrus 30 M. 25. epicyclus. a. 101/18. b. 311/30.“
„Saturni semidiametrus 2305/6. epicyclus. a. 1941/60. b. 617/30.“ - ↑ Damit dies war sei, müßte man annehmen, daß beim Mars anstatt 51/60 zu lesen sei 151/60. In der That stehen auch auf dem ebenerwähntem Blatte vor den eben angeführten Worten noch folgende:
„Eccentrotes Martis 6583“
„Epicyclus primus 1492“
„Epicyclus secundus 494;“ein Verhältniß, das dem genannten nahe kommt.
- ↑ Die ausführliche Erklärung siehe Revol. l. V. c. 3., vgl. M. C. 63.
- ↑ Vgl. Revol. l. VI. c. 1 sq.
- ↑ Partes (Teile) bedeutet vier Grade.
- ↑ „Vergilias.“ – Die in dieser Gruppe befindlichen Sterne wurden von den Römern Stellae Vergiliae genannt, weil ihr Aufgang vom Morgenhimmel den Frühling ankündete: „quod vere exoriuntur.“ Cic. in Arat. 2.
- ↑ Um das hier Gesagte zu verstehen, erinnere man sich, daß Coppernicus die sogenannte Kartenlinie (d. h. die Durchschnittslinie der Bahnebenen der Planeten mit der Ebene der Erdbahn) nicht in die Sonne verlegte, sondern in das Zentrum der Erdbahn; in Folge dessen schienen die Breiten des Planeten sonderbaren Schwankungen unterworfen, die eine Erklärung verlangten. Erschwert ward die Sache noch obendrein durch die irrtümlichen, auf Beobachtungsfehlern beruhenden Angaben älterer Astronomen. Die bezüglichen Auseinandersetzungen des Coppernicus haben nur mehr geschichtlichen Wert. –
- ↑ Geht der Planet auf zur Zeit des Sonnenunterganges, so befindet er sich in „Opposition.“
- ↑ Also zur Zeit der Conjunktion.
- ↑ Vgl. Anm. S. 39.
- ↑ Vgl. Revol. l. V. c. 20–23, l. VI. c. 5 sq.
- ↑ Dies stimmt ebenfalls mit den (Anm. 51 und 59) erwähnten Aufzeichnungen überein; dort heißt es nämlich: „Veneris semidiametrus 18. epicyclus a. 2/3 b. 1/4.“
- ↑ Nach den Worten „graduum duorum“ steht noch ein s ohne Ziffer; wohl ein Zeichen, daß hier noch ein Bruchtheil in „scrupuli“ beizufügen war.
- ↑ Statt „duplex non ostenditur“ muß es offenbar heißen duplex nobis ostenditur. Vgl. Rev. l. VI. c. 2.
- ↑ Vgl. die Figur im 2. Capitel des 6. Buches des Hauptwerkes; dort heißt es: „Vocant autem hunc planetae digressum obliquationem, alii reflexionem.“ Siehe die ausführlichere Beschreibung dieser eigenartigen Schwankung (deviatio) im 8. Kapitel der Revol. (l. VI.)
- ↑ Siehe die ausführlichere Beschreibung dieser eigenartigen Schwankung (deviatio) im 8. Kapitel der Revol. (l. VI.)
- ↑ Statt maxime illius deviationis punctus dürfte wohl (bei einmal angenommener neueren Schreibweise) richtiger maximae illius zu lesen sein; diese größte Schwankung liegt nämlich 30° von dem Durchschnittspunkte der Schwankungs-Bahnebene des Venus ab. – Cf. Riccioli Almagest, nov. I. 613, 638 sq.
- ↑ Statt deviationum liberamento continuatio ist wohl d. l. continuato zu setzen.
- ↑ Vgl. Rev. l. V, besonders c. 25 ff. (Nicht l. VI wie irrtümlich bei Prowe II. 200)
- ↑ Auch diese Werthe stimmen mit den in Anm. 59 erwähnten überein. An genannter Stelle heißt es: „Mercurii orbis 9. 24, Epicyclus a. 1. 411/4, h. 0. 333/4; colligunt 1, 71/2 (diversitas diametri 0. 29.“)
- ↑ Vgl. die Figur im 25. Kap. des 5. Buches der Revol. Wie aus der geschickten Zusammenstellung zweier kreisförmiger Bewegungen eine gradlinige hervorgehen kann, hat Coppernicus in seinem Hauptwerke ausführlich und schön bewiesen. (cf. l. III. c. 4.)
- ↑ In der Figur des angeführten Kapitels (l. III. c. 4) würde h der gradlinig bewegliche Mittelpunkt des Hauptepicykels sein, dabei h f = f d sein. Während das Kreischen um d einen Umlauf ausführt, kreiset das zweite zweimal in umgekehrter Richtung; so bewegt sich h in gerader Linie von a nach b und umgekehrt.






