Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper/Zweites Buch Teil A
| ← Erstes Buch | Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper (1879) von Nicolaus Copernicus |
Zweites Buch Teil B → |
Da wir in dem vorigen Buche im Ganzen drei Bewegungen der Erde nachgewiesen haben, durch die wir versprachen, alle Erscheinungen der Gestirne zu erklären: so wollen wir dadurch, dass wir sie der Reihe nach, einzeln, stückweise prüfen und untersuchen, dies nach Kräften thun. Wir beginnen aber mit der allerbekanntesten Kreisbewegung der Tages- und Nacht-Zeit, von welcher wir gesagt haben, dass sie von den Griechen Nychthemeron genannt werde, und die wir der Erdkugel am meisten und unmittelbar eigen angenommen haben, weil aus ihr Monate, Jahres- und andere vielnamige Zeiten, gleichwie die Zahl aus der Einheit, entstehen. Also über die Ungleichheit der Tage und Nächte, über Aufgang und Untergang der Sonne, der Theile des Thierkreises und der Sternbilder, und über dergleichen aus dieser Kreisbewegung sich Ergebendes, werden wir etwas Weniges sagen; zumal da Viele hierüber reichlich genug geschrieben haben, und dies doch mit dem Unsrigen auf Eins hinausläuft. Es kommt ja nichts darauf an, wenn wir, dasjenige, was Jene durch die ruhende Erde und die sich drehende Welt erklären, aus dem entgegengesetzten Gesichtspunkte betrachtend, zu demselben Ziele gelangen; weil es sich bei den Dingen, die wechselseitig sind, so verhält, dass das einander Entgegengesetzte übereinstimmt. Dennoch werden wir nichts von dem, was nöthig ist, übergehen. Aber Niemand darf sich wundern, wenn wir noch den Aufgang und Untergang der Sonne und der Sterne, und diesem Aehnliches einfach so benennen, sondern er wird wohl wissen, dass wir nur in der gewohnten Weise sprechen, die von Allen beibehalten werden kann, wenn sie nur im Sinne behalten, dass
Uns, die mit der Erd’ wir kreisen,
Sonn’ und Mond vorüberziehn
Sterne wechselnd wiederkehren
Oder scheidend sinken hin.
Aequinoctial-Kreis (Aequator) hat man den grössten aller, um die Pole der täglichen Kreisbewegung beschriebenen, Parallel-Kreise der Erdkugel genannt; Zodiakus (Ekliptik) aber den durch die Mitte der Zeichen beschriebenen Kreis, in welchem der Mittelpunkt der Erde selbst in jährlicher Kreisbewegung fortschreitet. Weil aber der Zodiakus gegen den Aequinoctialkreis schief steht, nach Maassgabe der Neigung der Erdaxe gegen ihn: so beschreibt er vermöge der täglichen Kreisbewegung der Erde auf beiden Seiten zwei ihn berührende Kreise, gleichsam als äusserste Grenzen seiner Schiefe, welche man Tropen (Wendekreise) nennt. Die Sonne scheint nämlich in diesen Kreisen Wenden (τροπάς), d. h. Umkehrungen zu machen, und zwar eine winterliche und eine sommerliche. Daher pflegte man auch denjenigen, welcher nördlich liegt den Sonnenstillstands-(solstitialis) Wendekreis, den andern südlichen den Wendekreis des kürzesten Tages (brumalis) zu nennen, wie es in der übersichtlichen Beschreibung der Kreisbewegungen der Erde weiter oben auseinandergesetzt ist. Hierauf folgt der sogenannte Horizont, den die Lateiner finientem (den Begrenzenden) nennen; indem er nämlich seinen Mittelpunkt auf der Oberfläche der Erde und seinen Pol in unserm Scheitel hat, begrenzt er den für uns sichtbaren Theil der Welt gegen denjenigen, welcher uns verborgen ist, und an welchem Alles das aufzugehen scheint, was untergeht. Weil aber die Erde mit der Unermesslichkeit des Himmels nicht zu vergleichen ist, da sogar nicht einmal der Raum, der zwischen Sonne und Mond liegt, nach unserer Annahme, mit der Grösse des Himmels verglichen werden kann: so scheint der Horizont den Himmel zu halbiren, als ob er durch den Mittelpunkt der Welt ginge, wie wir das im Anfange nachgewiesen haben. Insofern aber der Horizont schief gegen den Aequinoctialkreis steht, berührt auch er zwei Parallelkreise, und zwar einen nördlichen immer sichtbaren, und einen südlichen immer unsichtbaren; jenen nennt Proklus und die Griechen den Arctischen, diesen den Antarctischen; und diese Kreise werden nach Maassgabe der Schiefe des Horizonts oder der Höhe des Poles des Aequinoctialkreises, grösser oder kleiner. Es bleibt noch der Meridian, welcher sowohl durch die Pole des Horizonts, als auch durch die des Aequinoctialkreises geht, und deshalb senkrecht auf beiden Kreisen steht. Wenn die Sonne diesen Kreis erreicht, so bestimmt sie den Mittag und die Mitternacht. Da aber diese beiden Kreise, nämlich der Horizont und der Meridian, ihren Mittelpunkt in der Oberfläche der Erde haben: so folgen sie immer der Bewegung der Erde und unserm Auge. Das Auge hält sich nämlich überall für den Mittelpunkt der Sphäre alles ringsum Sichtbaren. Ferner übertragen auch alle auf der Erde angenommenen Kreise ihre entsprechenden Kreisbilder auf den Himmel, wie das in der Kosmographie bei den Dimensionen der Erde deutlicher nachgewiesen wird. Und zwar haben auch diese Kreise ihre eigenen Namen, wie denn [59] auch andere von unendlich vielen Arten und Namen bezeichnet werden könnten.
Da nun die Ekliptik zwischen den Wendekreis und Aequator als ein schräger Kreis auftritt, so halte ich es jetzt für nothwendig, dass wir den Abstand der Wendekreise und dann die Grösse des Neigungswinkels zwischen Aequator und Ekliptik untersuchen. Dies muss aber nothwendig durch die Sinne und durch Anwendung von Instrumenten bewirkt werden, bei welchen Letzteren das für die Hauptsache gehalten wird, dass ein Viereck aus Holz, oder besser aus einer andern, festeren Materie, aus Stein oder Metall bereitet wird, damit nicht etwa das bei Veränderung der Luft unbeständige Holz den Beobachter täuschen könne. Die eine Oberfläche desselben wird auf das Genaueste geebnet, und hat eine Breite von womöglich drei bis vier Ellen, damit sie für die anzubringende Eintheilung hinreicht. Nachdem nun in einer der Ecken der Mittelpunkt angenommen ist, wird ein Kreisquadrant so gross als möglich beschrieben, dieser in 90 gleiche Grade, und jeder derselben wieder in 60 Minuten, so genau als möglich, getheilt. Hierauf wird ein sehr gut gedrehter cylindrischer Stift im Mittelpunkte senkrecht gegen jene Oberfläche so errichtet, dass er ungefähr einen Finger breit oder weniger hervorragt. Nachdem dies Instrument so eingerichtet ist, bestimmt man die Mittagslinie auf einem in horizontaler Ebene gelegten Estrich, der so genau als möglich mittelst einer Wasserwage oder Libelle abgewogen ist, damit er nach keiner Seite abschüssig sei. Nachdem man nämlich auf diesem Estriche einen Kreis beschrieben hat, wird in dem Mittelpunkte desselben ein Stift errichtet, und bei zuweilen des Vormittages angestellten Beobachtungen angemerkt, wo die äusserste Spitze des Schattens die Peripherie des Kreises trifft. Ebenso machen wir es Nachmittags und halbiren den zwischen beiden Marken liegenden Kreisbogen. Auf diese Weise wird uns die vom Mittelpunkte durch den Halbirungspunkt gezogene grade Linie den Südpunkt und Nordpunkt unfehlbar angeben. Auf dieser Basis wird die Ebene des Instruments errichtet und senkrecht befestigt, und zwar so, dass, nachdem der Mittelpunkt nach Süden gewendet ist, die von diesem Mittelpunkte herabgehende grade Linie die Mittagslinie genau unter rechten Winkeln trifft. Auf diese Weise erreicht man es, dass die Oberfläche des Instrumentes den Meridiankreis enthält.
Nun müssen an dem Tage des Solstitiums und am kürzesten Tage die Schatten, welche jener Stift oder Cylinder des Mittags im Sonnenschein vom Mittelpunkte aus wirft, beobachtet werden, und nachdem irgend ein Gegenstand an der nach unten liegenden Peripherie des Quadranten angebracht ist, wodurch der Ort des Schattens genauer markirt werden kann, notiren [60] wir so genau als möglich die Mitte des Schattens in Graden und Minuten. Wenn wir dies gethan haben, so zeigt uns der Bogen, welcher zwischen dem solstitialen und brumalen Schatten sich markirt findet, den Abstand der Wendekreise und die ganze Schiefe der Ekliptik an, und wenn wir hiervon die Hälfte nehmen: so haben wir den Abstand des Wendekreises vom Aequator; und die Grösse des Neigungswinkels des Aequators gegen denjenigen Kreis, der durch die Mitte der Zeichen geht, ist dadurch bekannt. Ptolemäus nimmt dieses Intervall, was zwischen den genannten nördlichen und südlichen Grenzen liegt, zu 47° 42′ 40″,[1] so wie er dasselbe schon vorher von Hipparch und Eratosthenes beobachtet findet, nämlich als 11/83 des ganzen Kreises[2]; und hiervon die halbe Differenz, also 23° 51′ 20″,[3] ergab den Abstand der Wendekreise vom Aequator und den Neigungswinkel gegen die Ekliptik. Daher glaubte Ptolemäus, dass dies sich unveränderlich erhielte und immer bliebe. Aber es zeigt sich, dass diese Abstände von jener Zeit bis auf uns fortwährend abgenommen haben. Denn es ist von uns und einigen andern unserer Zeitgenossen der Abstand der Wendekreise nicht grösser als 46° 58′ gefunden, und der Neigungswinkel 23° 282/5′; so dass hinlänglich klar ist, dass die Schiefe der Ekliptik veränderlich sei, worüber ein Weiteres unten, wo wir auch zeigen werden, dass dieselbe, nach hinlänglich wahrscheinlicher Vermuthung, niemals grösser gewesen sei als 23° 52′ und niemals kleiner sein werde als 23° 28′.
Wie wir vom Horizonte gesagt haben, dass an ihm die Theile der Welt auf- und untergehen: so sagen wir jetzt, dass der Meridiankreis den Himmel halbirt, da er in einem Zeitraume von 24 Stunden sowohl die Ekliptik als auch den Aequator durchläuft und die Bogen derselben vom Frühlings- oder Herbstpunkte an einschneidet, und wiederum wird der von jenen eingeschlossene Bogen eingeschnitten. Da alle diese Kreise grösste Kreise sind: so bilden sie ein rechtwinkliges sphärisches Dreieck; denn der rechte Winkel rührt daher, dass der Meridian, nach dessen Definition, durch die Pole des Aequators geht. Man nennt aber den so eingeschlossenen Bogen des Meridians, oder irgend eines durch die Pole gehenden Kreises: die Declination dieses Theiles der Ekliptik; denjenigen Bogen aber, welcher auf dem Aequator dem mit ihm zugleich von demselben Punkte ausgehenden, ihn begleitenden Bogen der Ekliptik entspricht: Rectascension. Alles dies lässt sich leicht an einem sphärischen Dreiecke nachweisen. Es sei nämlich ein zugleich durch die Pole des Aequators und der Ekliptik gehender Kreis, welchen die Meisten den Colur der Solstitien nennen; die
[61] Hälfte der Ekliptik; die Hälfte des Aequators; der Frühlingspunkt im Punkte ; das Sommer-Solstitium in ; das Winter-Solstitium in ; der Pol der täglichen Kreisbewegung; und auf der Ekliptik werde der Bogen von z. B. 30 Graden genommen, und an ihm vorbei der Kreisquadrant gelegt.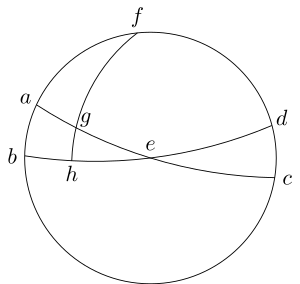


[63] zukomme: so finde ich im Verzeichnisse 11° 29′ und unter der Differenz: 11′, welche bei der grössten Schiefe, die wie gesagt 23° 52′ beträgt, ganz hinzuaddirt wird. Aber hier wird gesetzt: 23° 34′ ist um 6′ grösser als die kleinste Schiefe, dies ist der 4te Theil von den 24′, um welche die grösste Schiefe grösser ist, als die kleinste. In demselben Verhältnisse ist ungefähr 3 zu 11, und wenn ich nun 3 zu 11° 29′ hinzuaddire: so habe ich 11° 32′; und so viel beträgt die Declination des 30sten Grades der Ekliptik vom Nachtgleichenpunkte an gerechnet. Ebenso muss man bei den Winkeln und den Rectascensionen verfahren, nur muss man bei diesen immer da abziehen, wo man bei jenen addiren muss, damit Alles genau mit der Zeit fortschreite.
[64]
VERZEICHNISS DER DECLINATIONEN DER GRADE DER EKLIPTIK.
| |||||||||||
| Ekliptik | Declination | Differenz | Ekliptik | Declination | Differenz | Ekliptik | Declination | Differenz | |||
| Grade | Grade | Minuten | Minuten | Grade | Grade | Minuten | Minuten | Grade | Grade | Minuten | Minuten |
| 1 | 0 | 24 | 0 | 31 | 11 | 50 | 11 | 61 | 20 | 23 | 20 |
| 2 | 0 | 48 | 1 | 32 | 12 | 11 | 12 | 62 | 20 | 35 | 21 |
| 3 | 1 | 12 | 1 | 33 | 12 | 32 | 12 | 63 | 20 | 47 | 21 |
| 4 | 1 | 36 | 2 | 34 | 12 | 52 | 13 | 64 | 20 | 58 | 21 |
| 5 | 2 | 0 | 2 | 35 | 13 | 12 | 13 | 65 | 21 | 9 | 21 |
| 6 | 2 | 23 | 2 | 36 | 13 | 32 | 14 | 66 | 21 | 20 | 22 |
| 7 | 2 | 47 | 3 | 37 | 13 | 52 | 14 | 67 | 21 | 30 | 22 |
| 8 | 3 | 11 | 3 | 38 | 14 | 12 | 14 | 68 | 21 | 40 | 22 |
| 9 | 3 | 35 | 4 | 39 | 14 | 31 | 14 | 69 | 21 | 49 | 22 |
| 10 | 3 | 58 | 4 | 40 | 14 | 50 | 14 | 70 | 21 | 58 | 22 |
| 11 | 4 | 22 | 4 | 41 | 15 | 9 | 15 | 71 | 22 | 7 | 22 |
| 12 | 4 | 45 | 4 | 42 | 15 | 27 | 15 | 72 | 22 | 15 | 23 |
| 13 | 5 | 9 | 5 | 43 | 15 | 46 | 16 | 73 | 22 | 23 | 23 |
| 14 | 5 | 32 | 5 | 44 | 16 | 4 | 16 | 74 | 22 | 30 | 23 |
| 15 | 5 | 55 | 5 | 45 | 16 | 22 | 16 | 75 | 22 | 37 | 23 |
| 16 | 6 | 19 | 6 | 46 | 16 | 39 | 17 | 76 | 22 | 44 | 23 |
| 17 | 6 | 41 | 6 | 47 | 16 | 56 | 17 | 77 | 22 | 50 | 23 |
| 18 | 7 | 4 | 7 | 48 | 17 | 13 | 17 | 78 | 22 | 55 | 23 |
| 19 | 7 | 27 | 7 | 49 | 17 | 30 | 18 | 79 | 23 | 1 | 24 |
| 20 | 7 | 49 | 8 | 50 | 17 | 46 | 18 | 80 | 23 | 5 | 24 |
| 21 | 8 | 12 | 8 | 51 | 18 | 1 | 18 | 81 | 23 | 10 | 24 |
| 22 | 8 | 34 | 8 | 52 | 18 | 17 | 18 | 82 | 23 | 13 | 24 |
| 23 | 8 | 57 | 9 | 53 | 18 | 32 | 19 | 83 | 23 | 17 | 24 |
| 24 | 9 | 19 | 9 | 54 | 18 | 47 | 19 | 84 | 23 | 20 | 24 |
| 25 | 9 | 41 | 9 | 55 | 19 | 2 | 19 | 85 | 23 | 22 | 24 |
| 26 | 10 | 3 | 10 | 56 | 19 | 16 | 20 | 86 | 23 | 24 | 24 |
| 27 | 10 | 25 | 10 | 57 | 19 | 30 | 20 | 87 | 23 | 26 | 24 |
| 28 | 10 | 46 | 10 | 58 | 19 | 44 | 20 | 88 | 23 | 27 | 24 |
| 29 | 11 | 8 | 10 | 59 | 19 | 57 | 20 | 89 | 23 | 28 | 24 |
| 30 | 11 | 29 | 11 | 60 | 20 | 10 | 20 | 90 | 23 | 28 | 24 |
[65]
VERZEICHNISS DER RECTASCENSIONEN.
| |||||||||||
| Ekliptik | Zeiten | Differenz | Ekliptik | Zeiten | Differenz | Ekliptik | Zeiten | Differenz | |||
| Grade | Grade | Minuten | Minuten | Grade | Grade | Minuten | Minuten | Grade | Grade | Minuten | Minuten |
| 1 | 0 | 55 | 0 | 31 | 28 | 54 | 4 | 61 | 58 | 51 | 4 |
| 2 | 1 | 50 | 0 | 32 | 29 | 51 | 4 | 62 | 59 | 54 | 4 |
| 3 | 2 | 45 | 0 | 33 | 30 | 50 | 4 | 63 | 60 | 57 | 4 |
| 4 | 3 | 40 | 0 | 34 | 31 | 46 | 4 | 64 | 62 | 0 | 4 |
| 5 | 4 | 35 | 0 | 35 | 32 | 45 | 4 | 65 | 63 | 3 | 4 |
| 6 | 5 | 30 | 0 | 36 | 33 | 43 | 5 | 66 | 64 | 6 | 3 |
| 7 | 6 | 25 | 1 | 37 | 34 | 41 | 5 | 67 | 65 | 9 | 3 |
| 8 | 7 | 20 | 1 | 38 | 35 | 40 | 5 | 68 | 66 | 13 | 3 |
| 9 | 8 | 15 | 1 | 39 | 36 | 38 | 5 | 69 | 67 | 17 | 3 |
| 10 | 9 | 11 | 1 | 40 | 37 | 37 | 5 | 70 | 68 | 21 | 3 |
| 11 | 10 | 6 | 1 | 41 | 38 | 36 | 5 | 71 | 69 | 25 | 3 |
| 12 | 11 | 0 | 2 | 42 | 39 | 35 | 5 | 72 | 70 | 29 | 3 |
| 13 | 11 | 57 | 2 | 43 | 40 | 34 | 5 | 73 | 71 | 33 | 3 |
| 14 | 12 | 52 | 2 | 44 | 41 | 33 | 6 | 74 | 72 | 38 | 2 |
| 15 | 13 | 48 | 2 | 45 | 42 | 32 | 6 | 75 | 73 | 43 | 2 |
| 16 | 14 | 43 | 2 | 46 | 43 | 31 | 6 | 76 | 74 | 47 | 2 |
| 17 | 15 | 39 | 2 | 47 | 44 | 32 | 5 | 77 | 75 | 52 | 2 |
| 18 | 16 | 34 | 3 | 48 | 45 | 32 | 5 | 78 | 76 | 57 | 2 |
| 19 | 17 | 31 | 3 | 49 | 46 | 32 | 5 | 79 | 78 | 2 | 2 |
| 20 | 18 | 27 | 3 | 50 | 47 | 33 | 5 | 80 | 79 | 7 | 2 |
| 21 | 19 | 23 | 3 | 51 | 48 | 34 | 5 | 81 | 80 | 12 | 1 |
| 22 | 20 | 19 | 3 | 52 | 49 | 35 | 5 | 82 | 81 | 17 | 1 |
| 23 | 21 | 15 | 3 | 53 | 50 | 36 | 5 | 83 | 82 | 22 | 1 |
| 24 | 22 | 10 | 4 | 54 | 51 | 37 | 5 | 84 | 83 | 27 | 1 |
| 25 | 23 | 9 | 4 | 55 | 52 | 38 | 4 | 85 | 84 | 33 | 1 |
| 26 | 24 | 6 | 4 | 56 | 53 | 41 | 4 | 86 | 85 | 38 | 0 |
| 27 | 25 | 3 | 4 | 57 | 54 | 43 | 4 | 87 | 86 | 43 | 0 |
| 28 | 26 | 0 | 4 | 58 | 55 | 45 | 4 | 88 | 87 | 48 | 0 |
| 29 | 26 | 57 | 4 | 59 | 56 | 46 | 4 | 89 | 88 | 54 | 0 |
| 30 | 27 | 54 | 4 | 60 | 57 | 48 | 4 | 90 | 90 | 0 | 0 |
[66]
VERZEICHNISS DER MERIDIANWINKEL.
| |||||||||||
| Ekliptik | Winkel | Differenz | Ekliptik | Winkel | Differenz | Ekliptik | Winkel | Differenz | |||
| Grade | Grade | Minuten | Minuten | Grade | Grade | Minuten | Minuten | Grade | Grade | Minuten | Minuten |
| 1 | 66 | 32 | 24 | 31 | 69 | 35 | 21 | 61 | 78 | 7 | 12 |
| 2 | 66 | 33 | 24 | 32 | 69 | 48 | 21 | 62 | 78 | 29 | 12 |
| 3 | 66 | 34 | 24 | 33 | 70 | 0 | 20 | 63 | 78 | 51 | 11 |
| 4 | 66 | 35 | 24 | 34 | 70 | 13 | 20 | 64 | 79 | 14 | 11 |
| 5 | 66 | 37 | 24 | 35 | 70 | 26 | 20 | 65 | 79 | 36 | 11 |
| 6 | 66 | 39 | 24 | 36 | 70 | 39 | 20 | 66 | 79 | 59 | 10 |
| 7 | 66 | 42 | 24 | 37 | 70 | 53 | 20 | 67 | 80 | 22 | 10 |
| 8 | 66 | 44 | 24 | 38 | 71 | 7 | 19 | 68 | 80 | 45 | 10 |
| 9 | 66 | 47 | 24 | 39 | 71 | 22 | 19 | 69 | 81 | 9 | 9 |
| 10 | 66 | 51 | 24 | 40 | 71 | 36 | 19 | 70 | 81 | 33 | 9 |
| 11 | 66 | 55 | 24 | 41 | 71 | 52 | 19 | 71 | 81 | 58 | 8 |
| 12 | 66 | 59 | 24 | 42 | 72 | 8 | 18 | 72 | 82 | 22 | 8 |
| 13 | 67 | 4 | 23 | 43 | 72 | 24 | 18 | 73 | 82 | 46 | 7 |
| 14 | 67 | 10 | 23 | 44 | 72 | 39 | 18 | 74 | 83 | 11 | 7 |
| 15 | 67 | 15 | 23 | 45 | 72 | 55 | 17 | 75 | 83 | 35 | 6 |
| 16 | 67 | 21 | 23 | 46 | 73 | 11 | 17 | 76 | 84 | 0 | 6 |
| 17 | 67 | 27 | 23 | 47 | 73 | 28 | 17 | 77 | 84 | 25 | 6 |
| 18 | 67 | 34 | 23 | 48 | 73 | 47 | 17 | 78 | 84 | 50 | 5 |
| 19 | 67 | 41 | 23 | 49 | 74 | 6 | 16 | 79 | 85 | 15 | 5 |
| 20 | 67 | 49 | 23 | 50 | 74 | 24 | 16 | 80 | 85 | 40 | 4 |
| 21 | 67 | 56 | 23 | 51 | 74 | 42 | 16 | 81 | 86 | 5 | 4 |
| 22 | 68 | 4 | 22 | 52 | 75 | 1 | 15 | 82 | 86 | 30 | 3 |
| 23 | 68 | 13 | 22 | 53 | 75 | 21 | 15 | 83 | 86 | 55 | 3 |
| 24 | 68 | 22 | 22 | 54 | 75 | 40 | 15 | 84 | 87 | 19 | 3 |
| 25 | 68 | 32 | 22 | 55 | 76 | 1 | 14 | 85 | 87 | 53 | 2 |
| 26 | 68 | 41 | 22 | 56 | 76 | 21 | 14 | 86 | 88 | 17 | 2 |
| 27 | 68 | 51 | 22 | 57 | 76 | 42 | 14 | 87 | 88 | 41 | 1 |
| 28 | 69 | 2 | 21 | 58 | 77 | 3 | 13 | 88 | 89 | 6 | 1 |
| 29 | 69 | 13 | 21 | 59 | 77 | 24 | 13 | 89 | 89 | 33 | 0 |
| 30 | 69 | 24 | 21 | 60 | 77 | 45 | 13 | 90 | 90 | 0 | 0 |

[68]
Der Horizont ist bei der graden Kugel ein anderer als bei der schiefen. Horizont der graden Kugel heisst nämlich derjenige, gegen welchen der Aequator senkrecht steht, oder welcher durch die Pole des Aequators geht. Horizont der schiefen Kugel nennen wir denjenigen, gegen welchen der Aequator geneigt ist. Am graden Horizonte geht also Alles auf und unter, und Tage und Nächte sind gleich; denn dieser Horizont halbirt alle parallel mit der täglichen Bewegung beschriebenen Kreise, indem er durch ihre Pole geht; und es trifft hier Alles das zu, was wir schon über den Meridian entwickelt haben. Wir rechnen aber hier den Tag vom Aufgange der Sonne bis zu ihrem Untergange, nicht wie im gemeinen Leben von der Helligkeit bis zur Dunkelheit, d. h. von der Morgendämmerung bis zum Lichtanzünden; hierüber werden wir jedoch beim Auf- und Untergange der Sternenbilder noch mehreres sagen. Wo dagegen die Erdaxe senkrecht gegen den Horizont steht, geht Nichts auf oder unter, sondern Alles bleibt, während es sich im Kreise bewegt, immer sichtbar, oder unsichtbar, ausser demjenigen, was eine andere Bewegung heraufführt, wie z. B. die jährliche Bewegung um die Sonne, woraus folgt, dass dort der Tag ein halbes Jahr hindurch ununterbrochen dauert, und dass die übrige Zeit Nacht ist; und dies dient zu weiter nichts als zum Unterscheiden von Winter und Sommer, weil dort der Aequator mit dem Horizonte zusammenfällt. Aber bei der schiefen Kugel geht Einiges auf und unter, Einiges bleibt immer sichtbar oder unsichtbar, während Tage und Nächte ungleich werden. Wo ein schiefer Horizont existirt, berührt er zwei Parallelkreise, nach Maassgabe seiner Neigung, von denen derjenige, welcher dem sichtbaren Pole zu liegt, das immer Sichtbare, und der andere, welcher dem unsichtbaren Pole zu liegt, das immer Unsichtbare begrenzt. Der in die ganze Breite zwischen diese Grenzen fallende Horizont theilt alle dazwischen fallende Parallelkreise in ungleiche Bogen, ausser den Aequator, weil dieser der grösste Parallelkreis ist, und grösste Kreise sich gegenseitig halbiren. Der schiefe Horizont schneidet in der oberen Halbkugel von den nach den sichtbarem Pole zu liegenden Parallelkreisen grössere Bogen ab, als von denen, welche nach dem südlichen und unsichtbaren Pole zu liegen, und umgekehrt in der unsichtbaren Halbkugel; und da die Sonne in diesen Bogen bei der täglichen Bewegung erscheint, so bewirkt dies die Ungleichheit der Tage und Nächte.
Es giebt auch Unterschiede zwischen den mittägigen Schatten, wonach Einige Periskier, Andere Amphiskier, noch Andere Heteroskier genannt werden. Die Periskier können wir Ringsumschattende nennen, indem sie [69] rings um sich her Sonnenschatten werfen, und es sind diejenigen, deren Zenith oder Horizont-Pol weniger oder nicht mehr vom Erdpole absteht, als ein Wendekreis vom Aequator. Dort sind nämlich die Parallelkreise, welche der Horizont berührt, und welche die Grenzen des immer Sichtbaren oder Unsichtbaren bilden, grösser oder ebenso gross als die Wendekreise; und da deshalb im Sommer die Sonne in den immer sichtbaren Parallelkreisen erscheint: so wirft sie zu dieser Zeit die Schatten der Gnomonen nach allen Seiten. Wo aber der Horizont die Wendekreise berührt, da werden diese selbst die Grenzen des immer Sichtbaren und des immer Unsichtbaren. Deshalb scheint die Sonne im Solstitium um Mitternacht die Erde zu streifen, in welchem Augenblicke die ganze Ekliptik mit dem Horizonte zusammenfällt, und gleich darauf gehen sechs Himmelszeichen zugleich auf, und eben so viel an der entgegengesetzten Seite zugleich unter, und der Pol der Ekliptik fällt mit dem Pol des Horizontes zusammen. — Die Amphiskier, welche den mittägigen Schatten nach beiden Seiten werfen, wohnen zwischen den beiden Wendekreisen, welchen Raum die Alten die mittlere Zone nennen, und weil die Ekliptik in jener ganzen Gegend zweimal im Jahre rechtwinklig gegen den Horizont steht, wie dies im zweiten Lehrsatz der Phänomene des Euklid bewiesen wird: so nehmen dort die Schatten der Gnomonen zweimal ab, und während die Sonne von der einen Seite zur andern übergeht, werfen die Gnomonen bald nach Süden bald nach Norden Schatten. — Wir Anderen, die wir zwischen diesen und jenen wohnen, sind Heteroskier, weil wir nur nach der einen Seite, nämlich nach Norden mittägigen Schatten werfen. Die alten Mathematiker aber pflegten den Erdkreis in sieben Klimate zu theilen, nämlich durch die einzelnen Parallelkreise durch Meroë, durch Syëne, durch Alexandrien, durch Rhodus, durch den Hellespont, mitten durch den Pontus, durch die Mündung des Borysthenes, durch Byzanz u. s. w.[4] nach dem Unterschiede der längsten Tage, auch nach der Länge der Schatten, welche man zur Zeit der Aequinoctien und der beiden Sonnenwenden an den Gnomonen beobachtete, und nach der Polhöhe oder der Breite jedes Abschnittes. Da sich diese zum Theil mit der Zeit verändert haben: so sind sie nicht mehr dieselben, wie ehemals, wegen der schon erwähnten veränderlichen Schiefe der Ekliptik, welche die Alten nicht kannten; oder, um richtiger zu sprechen, wegen der sich ändernden Neigung des Aequators gegen die Ekliptik, wovon Jene abhängt. Aber die Polhöhen oder die Breiten der Oerter, und die Aequinoctial-Schatten stimmen mit denen überein, welche sich von Alters her aufgezeichnet finden, was deswegen so sein musste, weil der Aequator dem Pole der Erde folgt. Aus diesem Grunde werden auch jene Abschnitte durch irgend welche Bestimmungen der Schatten und Tage nicht hinreichend genau bezeichnet und begrenzt, sondern richtiger durch ihre Abstände vom Aequator, welche immer bleiben. Jene Aenderung der Wendekreise aber, obgleich sehr gering, bewirkt in den südlichen Gegenden eine geringe Verschiedenheit der Tage und Schatten, wird aber den nach Norden Reisenden bemerkbar. Es ist
[70] daher auch offenbar, was die Erscheinung der Schatten der Gnomonen begleitet, dass nämlich bei jeder gegebenen Höhe der Sonne, eine gewisse Länge des Schattens wahrgenommen wird, und umgekehrt.



[73] Radius des Parallelkreises 100000 enthält. Auch ergiebt sich als Hälfte der Sehne der ganzen Differenz des nachtgleichen Tages und des Parallels in Theilen, von denen der Parallelkreis 360 enthält. Hieraus ist klar, dass das Verhältniss zu aus zweien Verhältnissen bestehe, nämlich aus demjenigen der Sehne des doppelten zu der Sehne des doppelten , d. h. zu , und aus demjenigen der Sehne des doppelten zur Sehne des doppelten , d. h. zu ; zwischen und ist also die mittlere Proportionale. Ebenso setzen auch das Verhältniss von zu die Verhältnisse zu und zu zusammen. So glaube ich, dass nicht blos die Ungleichheit der Tage und Nächte, sondern auch des Mondes und der Sterne, deren Declination gegeben ist, und die Abschnitte der von ihnen vermöge der täglichen Bewegung beschriebenen Parallelkreise, welche über dem Horizonte liegen, von denen unterschieden werden, welche unter demselben sich befinden, woraus der Aufgang und Untergang derselben leicht erkannt werden kann.
[74]
Verzeichniss des Unterschiedes der Ascensionen bei der schiefen Kugel.
| |||||||||||||
| Declination | 31 | 32 | 33 | 34 | 35 | 36 | Polhöhe | ||||||
| Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | ||
| 1 | 0 | 36 | 0 | 37 | 0 | 39 | 0 | 40 | 0 | 42 | 0 | 44 | |
| 2 | 1 | 12 | 1 | 15 | 1 | 18 | 1 | 21 | 1 | 24 | 1 | 27 | |
| 3 | 1 | 48 | 1 | 53 | 1 | 57 | 2 | 2 | 2 | 6 | 2 | 11 | |
| 4 | 2 | 24 | 2 | 30 | 2 | 36 | 2 | 42 | 2 | 48 | 2 | 55 | |
| 5 | 3 | 1 | 3 | 8 | 3 | 15 | 3 | 23 | 3 | 31 | 3 | 39 | |
| 6 | 3 | 37 | 3 | 46 | 3 | 55 | 4 | 4 | 4 | 13 | 4 | 23 | |
| 7 | 4 | 14 | 4 | 24 | 4 | 34 | 4 | 45 | 4 | 56 | 5 | 7 | |
| 8 | 4 | 51 | 5 | 2 | 5 | 14 | 5 | 26 | 5 | 39 | 5 | 52 | |
| 9 | 5 | 28 | 5 | 41 | 5 | 54 | 6 | 8 | 6 | 22 | 6 | 36 | |
| 10 | 6 | 5 | 6 | 20 | 6 | 35 | 6 | 50 | 7 | 6 | 7 | 22 | |
| 11 | 6 | 42 | 6 | 59 | 7 | 15 | 7 | 32 | 7 | 49 | 8 | 7 | |
| 12 | 7 | 20 | 7 | 38 | 7 | 56 | 8 | 15 | 8 | 34 | 8 | 53 | |
| 13 | 7 | 58 | 8 | 18 | 8 | 37 | 8 | 58 | 9 | 18 | 9 | 39 | |
| 14 | 8 | 37 | 8 | 58 | 9 | 19 | 9 | 41 | 10 | 3 | 10 | 26 | |
| 15 | 9 | 16 | 9 | 38 | 10 | 1 | 10 | 25 | 10 | 49 | 11 | 14 | |
| 16 | 9 | 55 | 10 | 19 | 10 | 44 | 11 | 9 | 11 | 25 | 12 | 2 | |
| 17 | 10 | 35 | 11 | 1 | 11 | 27 | 11 | 54 | 12 | 22 | 12 | 50 | |
| 18 | 11 | 16 | 11 | 43 | 12 | 11 | 12 | 40 | 13 | 9 | 13 | 39 | |
| 19 | 11 | 56 | 12 | 25 | 12 | 55 | 13 | 26 | 13 | 57 | 14 | 29 | |
| 20 | 12 | 38 | 13 | 9 | 13 | 40 | 14 | 13 | 14 | 46 | 15 | 20 | |
| 21 | 13 | 20 | 13 | 53 | 14 | 26 | 15 | 0 | 15 | 36 | 16 | 12 | |
| 22 | 14 | 3 | 14 | 37 | 15 | 13 | 15 | 49 | 16 | 27 | 17 | 5 | |
| 23 | 14 | 47 | 15 | 23 | 16 | 0 | 16 | 38 | 17 | 17 | 17 | 58 | |
| 24 | 15 | 31 | 16 | 9 | 16 | 48 | 17 | 29 | 18 | 10 | 18 | 52 | |
| 25 | 16 | 16 | 16 | 56 | 17 | 38 | 18 | 20 | 19 | 3 | 19 | 48 | |
| 26 | 17 | 2 | 17 | 45 | 18 | 28 | 19 | 12 | 19 | 58 | 20 | 45 | |
| 27 | 17 | 50 | 18 | 34 | 19 | 19 | 20 | 6 | 20 | 54 | 21 | 44 | |
| 28 | 18 | 38 | 19 | 24 | 20 | 12 | 21 | 1 | 21 | 51 | 22 | 43 | |
| 29 | 19 | 27 | 20 | 16 | 21 | 6 | 21 | 57 | 22 | 50 | 23 | 45 | |
| 30 | 20 | 18 | 21 | 9 | 22 | 1 | 22 | 55 | 23 | 51 | 24 | 48 | |
| 31 | 21 | 10 | 22 | 3 | 22 | 58 | 23 | 55 | 24 | 53 | 25 | 53 | |
| 32 | 22 | 3 | 22 | 59 | 23 | 56 | 24 | 56 | 25 | 57 | 27 | 0 | |
| 33 | 22 | 57 | 23 | 54 | 24 | 19 | 25 | 59 | 27 | 3 | 28 | 9 | |
| 34 | 23 | 55 | 24 | 56 | 25 | 59 | 27 | 4 | 28 | 10 | 29 | 21 | |
| 35 | 24 | 53 | 25 | 57 | 27 | 3 | 28 | 10 | 29 | 21 | 30 | 35 | |
| 36 | 25 | 53 | 27 | 0 | 28 | 9 | 29 | 21 | 30 | 35 | 31 | 52 | |
[75]
Verzeichniss des Unterschiedes der Ascensionen bei der schiefen Kugel.
| |||||||||||||
| Declination | 37 | 38 | 39 | 40 | 41 | 42 | Polhöhe | ||||||
| Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | ||
| 1 | 0 | 45 | 0 | 47 | 0 | 49 | 0 | 50 | 0 | 52 | 0 | 54 | |
| 2 | 1 | 31 | 1 | 34 | 1 | 37 | 1 | 41 | 1 | 44 | 1 | 48 | |
| 3 | 2 | 16 | 2 | 21 | 2 | 26 | 2 | 31 | 2 | 37 | 2 | 42 | |
| 4 | 3 | 1 | 3 | 8 | 3 | 15 | 3 | 22 | 3 | 29 | 3 | 37 | |
| 5 | 3 | 47 | 3 | 55 | 4 | 4 | 4 | 13 | 4 | 22 | 4 | 31 | |
| 6 | 4 | 33 | 4 | 43 | 4 | 53 | 5 | 4 | 5 | 15 | 5 | 26 | |
| 7 | 5 | 19 | 5 | 30 | 5 | 42 | 5 | 55 | 6 | 8 | 6 | 21 | |
| 8 | 6 | 5 | 6 | 18 | 6 | 32 | 6 | 46 | 7 | 1 | 7 | 16 | |
| 9 | 6 | 51 | 7 | 6 | 7 | 22 | 7 | 38 | 7 | 55 | 8 | 12 | |
| 10 | 7 | 38 | 7 | 55 | 8 | 13 | 8 | 30 | 8 | 49 | 9 | 8 | |
| 11 | 8 | 25 | 8 | 44 | 9 | 3 | 9 | 23 | 9 | 44 | 10 | 5 | |
| 12 | 9 | 13 | 9 | 34 | 9 | 55 | 10 | 16 | 10 | 39 | 11 | 2 | |
| 13 | 10 | 1 | 10 | 24 | 10 | 46 | 11 | 10 | 11 | 35 | 12 | 0 | |
| 14 | 10 | 50 | 11 | 14 | 11 | 39 | 12 | 5 | 12 | 31 | 12 | 58 | |
| 15 | 11 | 39 | 12 | 5 | 12 | 32 | 13 | 0 | 13 | 28 | 13 | 58 | |
| 16 | 12 | 29 | 12 | 57 | 13 | 26 | 13 | 55 | 14 | 26 | 14 | 58 | |
| 17 | 13 | 19 | 13 | 49 | 14 | 20 | 14 | 52 | 15 | 25 | 15 | 59 | |
| 18 | 14 | 10 | 14 | 42 | 15 | 15 | 15 | 49 | 16 | 24 | 17 | 1 | |
| 19 | 15 | 2 | 15 | 36 | 16 | 11 | 16 | 48 | 17 | 25 | 18 | 4 | |
| 20 | 15 | 55 | 16 | 31 | 17 | 8 | 17 | 47 | 18 | 27 | 19 | 8 | |
| 21 | 16 | 49 | 17 | 27 | 18 | 7 | 18 | 47 | 19 | 30 | 20 | 13 | |
| 22 | 17 | 44 | 18 | 24 | 19 | 6 | 19 | 49 | 20 | 34 | 21 | 20 | |
| 23 | 18 | 39 | 19 | 22 | 20 | 6 | 20 | 52 | 21 | 39 | 22 | 28 | |
| 24 | 19 | 36 | 20 | 21 | 21 | 8 | 21 | 56 | 22 | 46 | 23 | 38 | |
| 25 | 20 | 34 | 21 | 21 | 22 | 11 | 23 | 2 | 23 | 55 | 24 | 50 | |
| 26 | 21 | 34 | 22 | 24 | 23 | 16 | 24 | 10 | 25 | 5 | 26 | 3 | |
| 27 | 22 | 35 | 23 | 28 | 24 | 22 | 25 | 19 | 26 | 17 | 27 | 18 | |
| 28 | 23 | 37 | 24 | 33 | 25 | 30 | 26 | 30 | 27 | 31 | 28 | 36 | |
| 29 | 24 | 41 | 25 | 40 | 26 | 40 | 27 | 43 | 28 | 48 | 29 | 57 | |
| 30 | 25 | 47 | 26 | 49 | 27 | 52 | 28 | 59 | 30 | 7 | 31 | 19 | |
| 31 | 26 | 55 | 28 | 0 | 29 | 7 | 30 | 17 | 31 | 29 | 32 | 45 | |
| 32 | 28 | 5 | 29 | 13 | 30 | 54 | 31 | 31 | 32 | 54 | 34 | 14 | |
| 33 | 29 | 18 | 30 | 29 | 31 | 44 | 33 | 1 | 34 | 22 | 35 | 47 | |
| 34 | 30 | 32 | 31 | 48 | 33 | 6 | 34 | 27 | 35 | 54 | 37 | 24 | |
| 35 | 31 | 51 | 33 | 10 | 34 | 33 | 35 | 59 | 37 | 30 | 39 | 5 | |
| 36 | 33 | 12 | 34 | 35 | 36 | 2 | 37 | 34 | 39 | 10 | 40 | 51 | |
[76]
Verzeichniss des Unterschiedes der Ascensionen bei der schiefen Kugel.
| |||||||||||||
| Declination | 43 | 44 | 45 | 46 | 47 | 48 | Polhöhe | ||||||
| Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | ||
| 1 | 0 | 56 | 0 | 58 | 1 | 0 | 1 | 2 | 1 | 4 | 1 | 7 | |
| 2 | 1 | 52 | 1 | 56 | 2 | 0 | 2 | 4 | 2 | 9 | 2 | 13 | |
| 3 | 2 | 48 | 2 | 54 | 3 | 0 | 3 | 7 | 3 | 13 | 3 | 20 | |
| 4 | 3 | 44 | 3 | 52 | 4 | 1 | 4 | 9 | 4 | 18 | 4 | 27 | |
| 5 | 4 | 41 | 4 | 51 | 5 | 1 | 5 | 12 | 5 | 23 | 5 | 35 | |
| 6 | 5 | 37 | 5 | 50 | 6 | 2 | 6 | 15 | 6 | 28 | 6 | 42 | |
| 7 | 6 | 34 | 6 | 49 | 7 | 3 | 7 | 18 | 7 | 34 | 7 | 50 | |
| 8 | 7 | 32 | 7 | 48 | 8 | 5 | 8 | 22 | 8 | 40 | 8 | 59 | |
| 9 | 8 | 30 | 8 | 48 | 9 | 7 | 9 | 26 | 9 | 47 | 10 | 8 | |
| 10 | 9 | 28 | 9 | 48 | 10 | 9 | 10 | 31 | 10 | 54 | 11 | 18 | |
| 11 | 10 | 27 | 10 | 49 | 11 | 13 | 11 | 37 | 12 | 2 | 12 | 28 | |
| 12 | 11 | 26 | 11 | 51 | 12 | 16 | 12 | 43 | 13 | 11 | 13 | 39 | |
| 13 | 12 | 26 | 12 | 53 | 13 | 21 | 13 | 50 | 14 | 20 | 14 | 51 | |
| 14 | 13 | 27 | 13 | 56 | 14 | 26 | 14 | 58 | 15 | 30 | 16 | 5 | |
| 15 | 14 | 28 | 15 | 0 | 15 | 32 | 16 | 7 | 16 | 42 | 17 | 19 | |
| 16 | 15 | 31 | 16 | 5 | 16 | 40 | 17 | 16 | 17 | 54 | 18 | 34 | |
| 17 | 16 | 34 | 17 | 10 | 17 | 48 | 18 | 27 | 19 | 8 | 19 | 51 | |
| 18 | 17 | 38 | 18 | 17 | 18 | 58 | 19 | 40 | 20 | 23 | 21 | 9 | |
| 19 | 18 | 44 | 19 | 25 | 20 | 9 | 20 | 53 | 21 | 40 | 22 | 29 | |
| 20 | 19 | 50 | 20 | 35 | 21 | 21 | 22 | 8 | 22 | 58 | 23 | 51 | |
| 21 | 20 | 59 | 21 | 46 | 22 | 34 | 23 | 25 | 24 | 18 | 25 | 14 | |
| 22 | 22 | 8 | 22 | 58 | 23 | 50 | 24 | 44 | 25 | 40 | 26 | 40 | |
| 23 | 23 | 19 | 24 | 12 | 25 | 7 | 26 | 5 | 27 | 5 | 28 | 8 | |
| 24 | 24 | 32 | 25 | 28 | 26 | 26 | 27 | 27 | 28 | 31 | 29 | 38 | |
| 25 | 25 | 47 | 26 | 46 | 27 | 48 | 28 | 52 | 30 | 0 | 31 | 12 | |
| 26 | 27 | 3 | 28 | 6 | 29 | 11 | 30 | 20 | 31 | 32 | 32 | 48 | |
| 27 | 28 | 22 | 29 | 29 | 30 | 38 | 31 | 51 | 33 | 7 | 34 | 28 | |
| 28 | 29 | 44 | 30 | 54 | 32 | 7 | 33 | 25 | 34 | 46 | 36 | 12 | |
| 29 | 31 | 8 | 32 | 22 | 33 | 40 | 35 | 2 | 36 | 28 | 38 | 0 | |
| 30 | 32 | 35 | 33 | 53 | 35 | 16 | 36 | 43 | 38 | 15 | 39 | 53 | |
| 31 | 34 | 5 | 35 | 28 | 36 | 56 | 38 | 29 | 40 | 7 | 41 | 52 | |
| 32 | 35 | 38 | 37 | 7 | 38 | 40 | 40 | 19 | 42 | 4 | 43 | 57 | |
| 33 | 37 | 16 | 38 | 50 | 40 | 30 | 42 | 15 | 44 | 8 | 46 | 9 | |
| 34 | 38 | 58 | 40 | 39 | 42 | 25 | 44 | 18 | 46 | 20 | 48 | 31 | |
| 35 | 40 | 46 | 42 | 33 | 44 | 27 | 46 | 23 | 48 | 36 | 51 | 3 | |
| 36 | 42 | 39 | 44 | 33 | 46 | 36 | 48 | 47 | 51 | 11 | 53 | 47 | |
[77]
Verzeichniss des Unterschiedes der Ascensionen bei der schiefen Kugel.
| |||||||||||||
| Declination | 49 | 50 | 51 | 52 | 53 | 54 | Polhöhe | ||||||
| Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | ||
| 1 | 1 | 9 | 1 | 12 | 1 | 14 | 1 | 17 | 1 | 20 | 1 | 23 | |
| 2 | 2 | 18 | 2 | 23 | 2 | 28 | 2 | 34 | 2 | 39 | 2 | 45 | |
| 3 | 3 | 27 | 3 | 35 | 3 | 43 | 3 | 51 | 3 | 59 | 4 | 8 | |
| 4 | 4 | 37 | 4 | 47 | 4 | 57 | 5 | 8 | 5 | 19 | 5 | 31 | |
| 5 | 5 | 47 | 5 | 50 | 6 | 12 | 6 | 26 | 6 | 40 | 6 | 55 | |
| 6 | 6 | 57 | 7 | 12 | 7 | 27 | 7 | 44 | 8 | 1 | 8 | 19 | |
| 7 | 8 | 7 | 8 | 25 | 8 | 43 | 9 | 2 | 9 | 23 | 9 | 44 | |
| 8 | 9 | 18 | 9 | 38 | 10 | 0 | 10 | 22 | 10 | 45 | 11 | 9 | |
| 9 | 10 | 30 | 10 | 53 | 11 | 17 | 11 | 42 | 12 | 8 | 12 | 35 | |
| 10 | 11 | 42 | 12 | 8 | 12 | 35 | 13 | 3 | 13 | 32 | 14 | 3 | |
| 11 | 12 | 55 | 13 | 24 | 13 | 53 | 14 | 24 | 14 | 57 | 15 | 31 | |
| 12 | 14 | 9 | 14 | 40 | 15 | 13 | 15 | 47 | 16 | 23 | 17 | 0 | |
| 13 | 15 | 24 | 15 | 58 | 16 | 34 | 17 | 11 | 17 | 50 | 18 | 32 | |
| 14 | 16 | 40 | 17 | 17 | 17 | 56 | 18 | 37 | 19 | 19 | 20 | 4 | |
| 15 | 17 | 57 | 18 | 39 | 19 | 19 | 20 | 4 | 20 | 50 | 21 | 38 | |
| 16 | 19 | 16 | 19 | 59 | 20 | 44 | 21 | 32 | 22 | 22 | 23 | 15 | |
| 17 | 20 | 36 | 21 | 22 | 22 | 11 | 23 | 2 | 23 | 56 | 24 | 53 | |
| 18 | 21 | 57 | 22 | 47 | 23 | 39 | 24 | 34 | 25 | 33 | 26 | 34 | |
| 19 | 23 | 20 | 24 | 14 | 25 | 10 | 26 | 9 | 27 | 11 | 28 | 17 | |
| 20 | 24 | 45 | 25 | 42 | 26 | 43 | 27 | 46 | 28 | 53 | 30 | 4 | |
| 21 | 26 | 12 | 27 | 14 | 28 | 18 | 29 | 26 | 30 | 37 | 31 | 54 | |
| 22 | 27 | 42 | 28 | 47 | 29 | 56 | 31 | 8 | 32 | 25 | 33 | 47 | |
| 23 | 29 | 14 | 30 | 23 | 31 | 37 | 32 | 54 | 34 | 17 | 35 | 45 | |
| 24 | 31 | 4 | 32 | 3 | 33 | 21 | 34 | 44 | 36 | 13 | 37 | 48 | |
| 25 | 32 | 26 | 33 | 46 | 35 | 10 | 36 | 39 | 38 | 14 | 39 | 59 | |
| 26 | 34 | 8 | 35 | 32 | 37 | 2 | 38 | 38 | 40 | 20 | 42 | 10 | |
| 27 | 35 | 53 | 37 | 23 | 39 | 0 | 40 | 42 | 42 | 33 | 44 | 32 | |
| 28 | 37 | 43 | 39 | 19 | 41 | 2 | 42 | 53 | 44 | 53 | 47 | 2 | |
| 29 | 39 | 37 | 41 | 21 | 43 | 12 | 45 | 12 | 47 | 21 | 49 | 44 | |
| 30 | 41 | 37 | 43 | 29 | 45 | 29 | 47 | 39 | 50 | 1 | 52 | 37 | |
| 31 | 43 | 44 | 45 | 44 | 47 | 54 | 50 | 16 | 52 | 53 | 55 | 48 | |
| 32 | 45 | 57 | 48 | 8 | 50 | 30 | 53 | 7 | 56 | 1 | 59 | 19 | |
| 33 | 48 | 19 | 50 | 44 | 53 | 20 | 56 | 13 | 59 | 28 | 63 | 21 | |
| 34 | 50 | 54 | 53 | 30 | 56 | 20 | 59 | 42 | 63 | 31 | 68 | 11 | |
| 35 | 53 | 40 | 56 | 34 | 59 | 58 | 63 | 40 | 68 | 18 | 74 | 32 | |
| 36 | 56 | 42 | 59 | 59 | 63 | 47 | 68 | 26 | 74 | 36 | 90 | 0 | |
[78]
Verzeichniss des Unterschiedes der Ascensionen bei der schiefen Kugel.
| |||||||||||||||
| Declination | 55 | 56 | 57 | 58 | 59 | 60 | Polhöhe | ||||||||
| Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | ||||
| 1 | 1 | 26 | 1 | 29 | 1 | 32 | 1 | 36 | 1 | 40 | 1 | 44 | |||
| 2 | 2 | 52 | 2 | 58 | 3 | 5 | 3 | 12 | 3 | 20 | 3 | 28 | |||
| 3 | 4 | 17 | 4 | 27 | 4 | 38 | 4 | 49 | 5 | 0 | 5 | 12 | |||
| 4 | 5 | 44 | 5 | 57 | 6 | 11 | 6 | 25 | 6 | 41 | 6 | 57 | |||
| 5 | 7 | 11 | 7 | 27 | 7 | 44 | 8 | 3 | 8 | 22 | 8 | 43 | |||
| 6 | 8 | 38 | 8 | 58 | 9 | 19 | 9 | 41 | 10 | 4 | 10 | 29 | |||
| 7 | 10 | 6 | 10 | 29 | 10 | 54 | 11 | 20 | 11 | 47 | 12 | 17 | |||
| 8 | 11 | 35 | 12 | 1 | 12 | 30 | 13 | 0 | 13 | 32 | 14 | 5 | |||
| 9 | 13 | 4 | 13 | 35 | 14 | 7 | 14 | 41 | 15 | 17 | 15 | 55 | |||
| 10 | 14 | 35 | 15 | 9 | 15 | 45 | 16 | 23 | 17 | 4 | 17 | 47 | |||
| 11 | 16 | 7 | 16 | 45 | 17 | 25 | 18 | 8 | 18 | 53 | 19 | 41 | |||
| 12 | 17 | 40 | 18 | 22 | 19 | 6 | 19 | 53 | 20 | 43 | 21 | 36 | |||
| 13 | 19 | 15 | 20 | 1 | 20 | 50 | 21 | 41 | 22 | 36 | 23 | 34 | |||
| 14 | 20 | 52 | 21 | 42 | 22 | 35 | 23 | 31 | 24 | 31 | 25 | 35 | |||
| 15 | 22 | 30 | 23 | 24 | 24 | 22 | 25 | 23 | 26 | 29 | 27 | 39 | |||
| 16 | 24 | 10 | 25 | 9 | 26 | 12 | 27 | 19 | 28 | 30 | 29 | 47 | |||
| 17 | 25 | 53 | 26 | 57 | 28 | 5 | 29 | 18 | 30 | 35 | 31 | 59 | |||
| 18 | 27 | 39 | 28 | 48 | 30 | 1 | 31 | 20 | 32 | 44 | 34 | 19 | |||
| 19 | 29 | 27 | 30 | 41 | 32 | 1 | 33 | 26 | 34 | 58 | 36 | 37 | |||
| 20 | 31 | 19 | 32 | 39 | 34 | 5 | 35 | 37 | 37 | 17 | 39 | 5 | |||
| 21 | 33 | 15 | 34 | 41 | 36 | 14 | 37 | 54 | 39 | 42 | 41 | 40 | |||
| 22 | 35 | 14 | 36 | 48 | 38 | 28 | 40 | 17 | 42 | 15 | 44 | 25 | |||
| 23 | 37 | 19 | 39 | 0 | 40 | 49 | 42 | 47 | 44 | 57 | 47 | 20 | |||
| 24 | 39 | 29 | 41 | 18 | 43 | 17 | 45 | 26 | 47 | 49 | 50 | 27 | |||
| 25 | 41 | 45 | 43 | 44 | 45 | 54 | 48 | 16 | 50 | 54 | 53 | 52 | |||
| 26 | 44 | 9 | 46 | 18 | 48 | 41 | 51 | 19 | 54 | 16 | 57 | 39 | |||
| 27 | 46 | 41 | 49 | 4 | 51 | 41 | 54 | 38 | 58 | 0 | 61 | 57 | |||
| 28 | 49 | 24 | 52 | 1 | 54 | 58 | 58 | 19 | 62 | 14 | 67 | 4 | |||
| 29 | 52 | 20 | 55 | 16 | 58 | 36 | 62 | 31 | 67 | 18 | 73 | 46 | |||
| 30 | 55 | 32 | 58 | 52 | 62 | 45 | 67 | 31 | 73 | 55 | 90 | 0 | |||
| 31 | 59 | 6 | 62 | 58 | 67 | 42 | 74 | 4 | 90 | 0 | |||||
| 32 | 63 | 10 | 67 | 53 | 74 | 12 | 90 | 0 | |||||||
| 33 | 68 | 1 | 74 | 19 | 90 | 0 | |||||||||
| 34 | 74 | 33 | 90 | 0 |
|
||||||||||
| 35 | 90 | 0 | |||||||||||||
| 36 | |||||||||||||||
Hieraus ist also klar, dass, wenn man die für die Declination der Sonne im Verzeichnisse unter der überschriebenen Polhöhe abgelesene Differenz, bei nördlicher Declination zum Kreisquadranten addirt, bei südlicher davon abzieht, und das Resultat mit zwei multiplicirt: man die Länge des fraglichen Tages erhält; und der Rest die Grösse des nächtlichen Bogens ist. Jede dieser beiden Angaben, durch 15 dividirt, ergiebt: wie viel gleiche Stunden eine jede von Beiden beträgt. Nimmt man aber den zwölften Theil: so erhält man den Zeitraum einer Zeitstunde, welche Stunden aber immer die Benennung ihres Tages erhalten, von welchem sie die zwölften Theile sind. Deshalb findet man Solstitial-, Aequinoctial- und Brumal-Stunden von den Alten angegeben. Ursprünglich waren keine anderen im Gebrauch, als die Zwölf zwischen Aufgang und Untergang, die Nacht aber theilte man in vier Vigilien oder Wachen; und der Gebrauch solcher Stunden erhielt sich durch die stillschweigende Uebereinkunft aller Völker lange Zeit: deshalb sind die Wasseruhren erfunden, bei welchen man mittelst Subtraction und Addition aus der Verschiedenheit des herabtröpfelnden Wassers die Tagesstunden bestimmte, damit auch bei Nebel die Zeittheilung wahrnehmbar bliebe. Später sind sowohl für die Tages- als auch Nacht-Zeit gemeinschaftliche und gleiche Stunden allgemein angenommen; und weil diese leichter zu beobachten sind, kamen jene Zeitstunden so sehr in Vergessenheit, dass, wenn man jetzt Jemanden aus dem Volke fragte, welche die erste, dritte, sechste, neunte, elfte Tagesstunde sei, er entweder nicht antworten könnte, oder wenigstens etwas sagen würde, was zur Sache gar nicht gehörte. Die Zahl dieser gleichen Stunden rechnen Einige von Mittag, Andere von Abend, Andere von Mitternacht, und Einige vom Aufgange der Sonne, je nachdem es in jedem Staate vorgeschrieben ist.
Nachdem so die Länge der Tage und Nächte, und ihre Unterschiede entwickelt sind, folgt in passlicher Ordnung, die Entwickelung der schrägen Aufsteigungen. Während jener Zeiten nämlich erheben sich die Dodecatemorien, d. h. die zwölf Theile der Ekliptik, oder irgend welche andere Bogen derselben; indem es keinen andern Unterschied der graden und schrägen Aufsteigung giebt, als denjenigen zwischen dem nachtgleichen und dem verschiedenen Tage, wie wir das gezeigt haben. Man hat nun die Dodecatemorien mit den erborgten Thiernamen, welche den Fixsternen angehören,
[80] benannt, und zwar vom Frühlingsnacht-Gleichenpunkte anfangend: Widder, Stier, Zwillinge, Krebs u. s. w. wie sie in der Reihe folgen.
Da die Ekliptik ausserdem ein gegen die Axe der Kugel schräg gerichteter Kreis ist: so bildet sie verschiedene Winkel mit dem Horizonte. Dass nie für Diejenigen, welche zwischen den Wendekreisen wohnen, zweimal senkrecht gegen Letzteren stehe, haben wir schon bei Gelegenheit der
[81] Verschiedenheit der Schatten gesagt. Es scheint mir aber für uns hinzureichen, wenn nur diejenigen Winkel nachgewiesen werden, welche den einseitig-schattenden Bewohnern, d. h. uns, dazu dienen, um aus denselben ihr Gesammtverhältniss leicht einzusehen. Dass nun bei der schiefen Kugel, wenn das Aequinoctium oder der Anfang des Widders aufgeht, die Ekliptik desto geneigter ist und sich dem Horizonte desto mehr nähert, je mehr ihre grösste südliche Declination, welche dem dann grade durch den Meridian gehenden Anfange des Steinbocks zukommt, beträgt; und umgekehrt, dass sie höher ist und einen grösseren Winkel im Osten bildet, wenn der Anfang der Waage aufgeht, und der Anfang des Krebses durch den Meridian geht; — das halte ich für hinreichend einleuchtend. Weil nun die drei Kreise: Aequator, Ekliptik und Horizont, in den Polen des Meridians sich gemeinschaftlich schneiden, so bestimmen dessen von jenen begrenzte Bogen: wie gross jener östliche Winkel gerechnet werden muss.
[82] zu 6 Graden fortschreitend, von demjenigen Parallelkreise an, dessen Polhöhe 39 Grad beträgt, von 3 zu 3 Graden fortschreitend, bis zu demjenigen, der 57 Grad Polhöhe hat. Die dritte enthält die mit dem Horizonte gebildeten Winkel, auch von 6 zu 6 Graden und unter denselben 7 Rubriken. Und alles dies nach der kleinsten Schiefe der Ekliptik von 23 Grad 28 Minuten, welche in unserm Jahrhundert ungefähr zutrifft.
[83]
Verzeichniss der Aufsteigungen der Zeichen bei der Umdrehung der graden Kugel.
| ||||||||||||
| Ekliptik | Aufsteigung | Für den einzelnen Grad | Ekliptik | Aufsteigung | Für den einzelnen Grad | |||||||
| Zeichen | Grad | Grad | Min. | Grad | Min. | Zeichen | Grad | Grad | Min. | Grad | Min. | |
| ♈︎ | 6 | 5 | 30 | 0 | 55 | ♎︎ | 6 | 185 | 30 | 0 | 55 | |
| 12 | 11 | 0 | 0 | 55 | 12 | 191 | 0 | 0 | 55 | |||
| 18 | 16 | 34 | 0 | 56 | 18 | 196 | 34 | 0 | 56 | |||
| 24 | 22 | 10 | 0 | 56 | 24 | 202 | 10 | 0 | 56 | |||
| 30 | 27 | 54 | 0 | 57 | 30 | 207 | 54 | 0 | 57 | |||
| ♉︎ | 6 | 33 | 43 | 0 | 58 | ♏︎ | 6 | 213 | 43 | 0 | 58 | |
| 12 | 39 | 35 | 0 | 59 | 12 | 219 | 35 | 0 | 59 | |||
| 18 | 45 | 32 | 1 | 0 | 18 | 225 | 32 | 1 | 0 | |||
| 24 | 51 | 37 | 1 | 1 | 24 | 231 | 37 | 1 | 1 | |||
| 30 | 57 | 48 | 1 | 2 | 30 | 237 | 48 | 1 | 2 | |||
| ♊︎ | 6 | 64 | 6 | 1 | 3 | ♐︎ | 6 | 244 | 6 | 1 | 3 | |
| 12 | 70 | 29 | 1 | 4 | 12 | 250 | 29 | 1 | 4 | |||
| 18 | 76 | 57 | 1 | 5 | 18 | 256 | 57 | 1 | 5 | |||
| 24 | 83 | 27 | 1 | 5 | 24 | 263 | 27 | 1 | 5 | |||
| 30 | 90 | 0 | 1 | 5 | 30 | 270 | 0 | 1 | 5 | |||
| ♋︎ | 6 | 96 | 33 | 1 | 5 | ♑︎ | 6 | 276 | 33 | 1 | 5 | |
| 12 | 103 | 3 | 1 | 5 | 12 | 283 | 3 | 1 | 5 | |||
| 18 | 109 | 31 | 1 | 5 | 18 | 289 | 31 | 1 | 5 | |||
| 24 | 115 | 54 | 1 | 4 | 24 | 295 | 54 | 1 | 4 | |||
| 30 | 122 | 12 | 1 | 3 | 30 | 302 | 12 | 1 | 3 | |||
| ♌︎ | 6 | 128 | 23 | 1 | 2 | ♒︎ | 6 | 308 | 23 | 1 | 2 | |
| 12 | 134 | 28 | 1 | 1 | 12 | 314 | 28 | 1 | 1 | |||
| 18 | 140 | 25 | 1 | 0 | 18 | 320 | 25 | 1 | 0 | |||
| 24 | 146 | 17 | 0 | 59 | 24 | 326 | 17 | 0 | 59 | |||
| 30 | 152 | 6 | 0 | 58 | 30 | 332 | 6 | 0 | 58 | |||
| ♍︎ | 6 | 157 | 50 | 0 | 57 | ♓︎ | 6 | 337 | 50 | 0 | 57 | |
| 12 | 163 | 26 | 0 | 56 | 12 | 343 | 26 | 0 | 56 | |||
| 18 | 169 | 0 | 0 | 56 | 18 | 349 | 0 | 0 | 56 | |||
| 24 | 174 | 30 | 0 | 55 | 24 | 354 | 30 | 0 | 55 | |||
| 30 | 180 | 0 | 0 | 55 | 30 | 360 | 0 | 0 | 55 | |||
[84]
Tafel der Aufsteigungen an der schiefen Kugel.
| |||||||||||||||
| Polhöhe | 39 | 42 | 45 | 48 | 51 | 54 | 57 | ||||||||
| Ekliptik | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | ||||||||
| Zeichen | Grad | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. |
| ♈︎ | 6 | 3 | 34 | 3 | 20 | 3 | 6 | 2 | 50 | 2 | 32 | 2 | 12 | 1 | 49 |
| 12 | 7 | 10 | 6 | 44 | 6 | 15 | 5 | 44 | 5 | 8 | 4 | 27 | 3 | 40 | |
| 18 | 10 | 50 | 10 | 10 | 9 | 27 | 8 | 39 | 7 | 47 | 6 | 44 | 5 | 34 | |
| 24 | 14 | 32 | 13 | 39 | 12 | 43 | 11 | 40 | 10 | 28 | 9 | 7 | 7 | 32 | |
| 30 | 18 | 26 | 17 | 21 | 16 | 11 | 14 | 51 | 13 | 26 | 11 | 40 | 9 | 40 | |
| ♉︎ | 6 | 22 | 30 | 21 | 12 | 19 | 46 | 18 | 14 | 16 | 25 | 14 | 22 | 11 | 57 |
| 12 | 26 | 39 | 25 | 10 | 23 | 32 | 21 | 42 | 19 | 38 | 17 | 13 | 14 | 23 | |
| 18 | 31 | 0 | 29 | 20 | 27 | 29 | 25 | 24 | 23 | 2 | 20 | 17 | 17 | 2 | |
| 24 | 35 | 38 | 33 | 47 | 31 | 43 | 29 | 25 | 26 | 47 | 23 | 42 | 20 | 2 | |
| 30 | 40 | 30 | 38 | 30 | 36 | 15 | 33 | 41 | 30 | 49 | 27 | 26 | 23 | 22 | |
| ♊︎ | 6 | 45 | 39 | 43 | 31 | 41 | 7 | 38 | 23 | 35 | 15 | 31 | 34 | 27 | 7 |
| 12 | 51 | 8 | 48 | 52 | 46 | 20 | 43 | 27 | 40 | 8 | 36 | 13 | 31 | 26 | |
| 18 | 56 | 56 | 54 | 35 | 51 | 56 | 48 | 56 | 45 | 28 | 41 | 22 | 36 | 20 | |
| 24 | 63 | 0 | 60 | 36 | 57 | 54 | 54 | 49 | 51 | 15 | 47 | 1 | 41 | 49 | |
| 30 | 69 | 25 | 66 | 59 | 64 | 16 | 61 | 10 | 57 | 34 | 53 | 28 | 48 | 2 | |
| ♋︎ | 6 | 76 | 6 | 73 | 42 | 71 | 0 | 67 | 55 | 64 | 21 | 60 | 7 | 54 | 55 |
| 12 | 83 | 2 | 80 | 41 | 78 | 2 | 75 | 2 | 71 | 34 | 67 | 28 | 62 | 26 | |
| 18 | 90 | 10 | 87 | 54 | 85 | 22 | 82 | 29 | 79 | 10 | 75 | 15 | 70 | 28 | |
| 24 | 97 | 27 | 95 | 19 | 92 | 55 | 90 | 11 | 87 | 3 | 83 | 22 | 78 | 55 | |
| 30 | 104 | 54 | 102 | 54 | 100 | 39 | 98 | 5 | 95 | 13 | 91 | 50 | 87 | 46 | |
| ♌︎ | 6 | 112 | 24 | 110 | 33 | 108 | 30 | 106 | 11 | 103 | 33 | 100 | 28 | 96 | 48 |
| 12 | 119 | 56 | 118 | 16 | 116 | 25 | 114 | 20 | 111 | 58 | 109 | 13 | 105 | 58 | |
| 18 | 127 | 29 | 126 | 0 | 124 | 23 | 122 | 32 | 120 | 28 | 118 | 3 | 115 | 13 | |
| 24 | 135 | 4 | 133 | 46 | 132 | 21 | 130 | 48 | 128 | 59 | 126 | 56 | 124 | 31 | |
| 30 | 142 | 38 | 141 | 33 | 140 | 23 | 139 | 3 | 137 | 38 | 135 | 52 | 133 | 52 | |
| ♍︎ | 6 | 150 | 11 | 149 | 19 | 148 | 23 | 147 | 20 | 146 | 8 | 144 | 47 | 143 | 12 |
| 12 | 157 | 41 | 157 | 1 | 156 | 19 | 155 | 29 | 154 | 38 | 153 | 36 | 153 | 24 | |
| 18 | 165 | 7 | 164 | 40 | 164 | 12 | 163 | 41 | 163 | 5 | 162 | 24 | 162 | 47 | |
| 24 | 172 | 34 | 172 | 21 | 172 | 6 | 171 | 51 | 171 | 33 | 171 | 12 | 170 | 49 | |
| 30 | 180 | 0 | 180 | 0 | 180 | 0 | 180 | 0 | 180 | 0 | 180 | 0 | 180 | 0 | |
[85]
Tafel der Aufsteigungen an der schiefen Kugel.
| |||||||||||||||
| Polhöhe | 39 | 42 | 45 | 48 | 51 | 54 | 57 | ||||||||
| Ekliptik | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | Aufsteigung | ||||||||
| Zeichen | Grad | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. |
| ♎︎ | 6 | 187 | 26 | 187 | 39 | 187 | 54 | 188 | 9 | 188 | 27 | 188 | 48 | 189 | 11 |
| 12 | 194 | 53 | 195 | 19 | 195 | 48 | 196 | 19 | 196 | 55 | 197 | 36 | 198 | 23 | |
| 18 | 202 | 21 | 203 | 0 | 203 | 41 | 204 | 30 | 205 | 24 | 206 | 25 | 207 | 36 | |
| 24 | 209 | 49 | 210 | 41 | 211 | 37 | 212 | 40 | 213 | 52 | 215 | 13 | 216 | 48 | |
| 30 | 217 | 22 | 218 | 27 | 219 | 37 | 220 | 57 | 222 | 22 | 224 | 8 | 226 | 8 | |
| ♏︎ | 6 | 224 | 56 | 226 | 14 | 227 | 38 | 229 | 12 | 231 | 1 | 233 | 4 | 235 | 29 |
| 12 | 232 | 56 | 234 | 0 | 235 | 37 | 237 | 28 | 239 | 32 | 241 | 57 | 244 | 47 | |
| 18 | 240 | 31 | 241 | 44 | 243 | 35 | 245 | 40 | 248 | 2 | 250 | 47 | 254 | 2 | |
| 24 | 247 | 36 | 249 | 27 | 251 | 30 | 253 | 49 | 256 | 27 | 259 | 32 | 263 | 12 | |
| 30 | 255 | 36 | 257 | 6 | 259 | 21 | 261 | 52 | 264 | 47 | 268 | 10 | 272 | 14 | |
| ♐︎ | 6 | 262 | 8 | 264 | 41 | 267 | 5 | 269 | 49 | 272 | 57 | 276 | 38 | 281 | 5 |
| 12 | 269 | 50 | 272 | 6 | 274 | 38 | 277 | 31 | 280 | 50 | 284 | 45 | 289 | 32 | |
| 18 | 276 | 58 | 279 | 19 | 281 | 58 | 248 | 58 | 288 | 26 | 292 | 32 | 297 | 34 | |
| 24 | 283 | 54 | 286 | 18 | 289 | 0 | 292 | 5 | 295 | 39 | 299 | 53 | 305 | 5 | |
| 30 | 290 | 35 | 293 | 1 | 295 | 45 | 298 | 50 | 302 | 26 | 306 | 42 | 311 | 58 | |
| ♑︎ | 6 | 297 | 0 | 299 | 24 | 302 | 6 | 305 | 11 | 308 | 45 | 312 | 59 | 318 | 11 |
| 12 | 303 | 4 | 305 | 25 | 308 | 4 | 311 | 4 | 314 | 32 | 318 | 38 | 323 | 40 | |
| 18 | 308 | 52 | 311 | 8 | 313 | 40 | 316 | 33 | 319 | 52 | 323 | 47 | 328 | 34 | |
| 24 | 314 | 21 | 316 | 29 | 318 | 53 | 321 | 37 | 324 | 45 | 328 | 26 | 332 | 53 | |
| 30 | 319 | 30 | 321 | 30 | 323 | 45 | 326 | 19 | 329 | 11 | 332 | 34 | 336 | 38 | |
| ♒︎ | 6 | 324 | 21 | 326 | 13 | 328 | 16 | 330 | 35 | 333 | 13 | 336 | 18 | 339 | 58 |
| 12 | 330 | 0 | 330 | 40 | 332 | 31 | 334 | 36 | 336 | 58 | 339 | 43 | 342 | 58 | |
| 18 | 333 | 21 | 334 | 50 | 336 | 27 | 338 | 18 | 340 | 22 | 342 | 47 | 345 | 37 | |
| 24 | 337 | 30 | 338 | 48 | 340 | 3 | 341 | 46 | 343 | 35 | 345 | 38 | 348 | 3 | |
| 30 | 341 | 34 | 342 | 39 | 343 | 49 | 345 | 9 | 346 | 34 | 348 | 20 | 350 | 20 | |
| ♓︎ | 6 | 345 | 29 | 346 | 21 | 347 | 17 | 348 | 20 | 349 | 32 | 350 | 53 | 352 | 28 |
| 12 | 349 | 11 | 349 | 51 | 350 | 33 | 351 | 21 | 352 | 14 | 353 | 16 | 354 | 26 | |
| 18 | 352 | 50 | 353 | 16 | 353 | 45 | 354 | 16 | 354 | 52 | 355 | 33 | 356 | 20 | |
| 24 | 356 | 26 | 356 | 40 | 356 | 23 | 357 | 10 | 357 | 53 | 357 | 48 | 358 | 11 | |
| 30 | 360 | 0 | 360 | 0 | 360 | 0 | 360 | 0 | 360 | 0 | 360 | 0 | 360 | 0 | |
[86]
Tafel der Winkel, welche die Ekliptik mit dem Horizonte bildet.
| |||||||||||||||||
| Polhöhe | 39 | 42 | 45 | 48 | 51 | 54 | 57 | Polhöhe | |||||||||
| Ekliptik | Winkel | Winkel | Winkel | Winkel | Winkel | Winkel | Winkel | Ekliptik | |||||||||
| Zeichen | Grad | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Min. | Grad | Zeichen |
| ♈︎ | 0 | 27 | 32 | 24 | 32 | 21 | 32 | 18 | 32 | 15 | 32 | 12 | 32 | 9 | 32 | 30 | |
| 6 | 27 | 37 | 24 | 36 | 21 | 36 | 18 | 36 | 15 | 35 | 12 | 35 | 9 | 35 | 24 | ||
| 12 | 27 | 49 | 24 | 49 | 21 | 48 | 18 | 47 | 15 | 45 | 12 | 43 | 9 | 41 | 18 | ||
| 18 | 28 | 13 | 25 | 9 | 22 | 6 | 19 | 3 | 15 | 59 | 12 | 56 | 9 | 53 | 12 | ||
| 24 | 28 | 45 | 25 | 40 | 22 | 34 | 19 | 29 | 16 | 23 | 13 | 18 | 10 | 13 | 6 | ♓︎ | |
| 30 | 29 | 27 | 26 | 15 | 23 | 11 | 20 | 5 | 16 | 56 | 13 | 45 | 10 | 31 | 30 | ||
| ♉︎ | 6 | 30 | 19 | 27 | 9 | 23 | 59 | 20 | 48 | 17 | 34 | 14 | 20 | 11 | 2 | 24 | |
| 12 | 31 | 21 | 28 | 9 | 24 | 56 | 21 | 41 | 18 | 23 | 15 | 3 | 11 | 40 | 18 | ||
| 18 | 32 | 35 | 29 | 20 | 26 | 3 | 22 | 43 | 19 | 21 | 15 | 56 | 12 | 26 | 12 | ||
| 24 | 34 | 5 | 30 | 43 | 27 | 23 | 24 | 2 | 20 | 41 | 16 | 59 | 13 | 20 | 6 | ♒︎ | |
| 30 | 35 | 40 | 32 | 17 | 28 | 52 | 25 | 26 | 21 | 52 | 18 | 14 | 14 | 26 | 30 | ||
| ♊︎ | 6 | 37 | 29 | 34 | 1 | 30 | 37 | 27 | 5 | 23 | 11 | 19 | 42 | 15 | 48 | 24 | |
| 12 | 39 | 32 | 36 | 4 | 32 | 32 | 28 | 56 | 25 | 15 | 21 | 25 | 17 | 23 | 18 | ||
| 18 | 41 | 44 | 38 | 14 | 34 | 41 | 31 | 3 | 27 | 18 | 23 | 25 | 19 | 16 | 12 | ||
| 24 | 44 | 8 | 40 | 32 | 37 | 2 | 33 | 22 | 29 | 35 | 25 | 37 | 21 | 26 | 6 | ♑︎ | |
| 30 | 46 | 41 | 43 | 11 | 39 | 33 | 35 | 53 | 32 | 5 | 28 | 6 | 23 | 52 | 30 | ||
| ♋︎ | 6 | 49 | 18 | 45 | 51 | 42 | 15 | 38 | 35 | 34 | 44 | 30 | 50 | 26 | 36 | 24 | |
| 12 | 52 | 3 | 48 | 34 | 45 | 0 | 41 | 8 | 37 | 55 | 33 | 43 | 29 | 34 | 18 | ||
| 18 | 54 | 44 | 51 | 20 | 47 | 48 | 44 | 13 | 40 | 31 | 36 | 40 | 32 | 39 | 12 | ||
| 24 | 57 | 30 | 54 | 5 | 50 | 38 | 47 | 6 | 43 | 33 | 39 | 43 | 35 | 50 | 6 | ♐︎ | |
| 30 | 60 | 4 | 56 | 42 | 53 | 22 | 49 | 54 | 46 | 21 | 42 | 43 | 38 | 56 | 30 | ||
| ♌︎ | 6 | 62 | 40 | 59 | 27 | 56 | 0 | 52 | 34 | 49 | 9 | 45 | 37 | 41 | 57 | 24 | |
| 12 | 64 | 59 | 61 | 44 | 58 | 26 | 55 | 7 | 51 | 46 | 48 | 19 | 44 | 48 | 18 | ||
| 18 | 67 | 7 | 63 | 56 | 60 | 20 | 57 | 26 | 54 | 6 | 50 | 47 | 47 | 24 | 12 | ||
| 24 | 68 | 59 | 65 | 52 | 62 | 42 | 59 | 30 | 56 | 17 | 53 | 7 | 49 | 47 | 6 | ♏︎ | |
| 30 | 70 | 38 | 67 | 27 | 64 | 18 | 61 | 17 | 58 | 9 | 54 | 58 | 52 | 38 | 30 | ||
| ♍︎ | 6 | 72 | 0 | 68 | 53 | 65 | 51 | 62 | 46 | 59 | 37 | 56 | 27 | 53 | 16 | 24 | |
| 12 | 73 | 4 | 70 | 2 | 66 | 59 | 63 | 56 | 60 | 53 | 57 | 50 | 54 | 46 | 18 | ||
| 18 | 73 | 51 | 70 | 50 | 67 | 49 | 64 | 48 | 61 | 46 | 58 | 45 | 55 | 44 | 12 | ||
| 24 | 74 | 19 | 71 | 20 | 68 | 20 | 65 | 19 | 62 | 18 | 59 | 17 | 56 | 16 | 6 | ||
| 30 | 74 | 28 | 71 | 28 | 68 | 28 | 65 | 28 | 62 | 28 | 59 | 28 | 56 | 28 | 0 | ♎︎ | |
Der Gebrauch dieser Tafeln ergiebt sich schon aus ihrer Entwicklung. Wenn man nämlich die Rectascension für einen bekannten Grad der Sonne nimmt, zu derselben für jede gleiche Stunde 15 Grad addirt, und jede 360 Grade eines vollen Kreises, — falls die Summe grösser geworden ist, — davon abzieht; so ergiebt der Rest der Rectascension den Grad der Ekliptik, welcher zu der gegebenen Zeit, vom Mittag an gerechnet, culminirt. Ebenso, wenn man für die schiefe Aufsteigung seiner Gegend dasselbe thut: so hat man den, zu der vom Aufgange der Sonne an zurückgerechneten Zeit aufgehenden Punkt der Ekliptik. Auch für beliebige ausserhalb der Ekliptik befindliche Sterne, deren Rectascensionen bekannt sind, ergiebt sich, wie oben gezeigt ist, aus dem Verzeichnisse derjenige Punkt der Ekliptik, welcher bei gleicher Rectascension vom Anfang des Widders gerechnet, mit denselben zugleich den Meridian passirt; und aus ihrer schiefen Aufsteigung ergiebt sich, welcher Punkt der Ekliptik mit ihnen zugleich aufgeht, je nachdem sich die Aufsteigungen und Grade der Ekliptik an den betreffenden Stellen der Tafeln finden. Auf gleiche Weise, aber an immer entgegengesetzten Stellen, wird man beim Untergange verfahren. Wenn ferner zu derjenigen Rectascension, welche culminirt, ein Viertelkreis addirt wird: so erhält man die schiefe Aufsteigung des aufgehenden Sternes. Es ergiebt sich also aus dem culminirenden Grade auch der aufgehende und umgekehrt. Es folgt die Tafel der Winkel, welche die Ekliptik mit dem Horizonte bildet, und welche nach dem aufgehenden Grade der Ekliptik abgelesen werden. Hieraus wird auch ersehen, um wie viel sich der 90ste Grad der Ekliptik über dem Horizonte erhebt, was bei Sonnenfinsternissen sehr nothwendig zu wissen ist.
Wir gehen dazu über, das Verhältniss der Winkel und Bogen, welche an den Schnittpunkten der Ekliptik und der Kreise entstehen, welche durch den Pol des Horizontes gehen und auf denen auch die Höhe über dem Horizonte gemessen wird, auseinander zu setzen. Nun ist aber über die Höhe der Sonne im Meridian, oder irgend eines beliebigen culminirenden Grades der Ekliptik und über den Winkel, unter welchem letztere den Meridian schneidet, bereits oben gehandelt; da ja der Meridian selbst einer jener Kreise ist, welche durch den Scheitel des Horizonts gezogen sind. Auch von dem Winkel am Aufgangspunkte ist schon vorhin die Rede gewesen, indem sein Complement der Winkel ist, welchen der Quadrant des Viertelkreises mit der aufgehenden Ekliptik einschliesst. Es bleibt also noch übrig, unter Beibehaltung [88] der früheren Figur, über die zwischenliegenden Schnittpunkte des Meridians und der Halbkreise der Ekliptik und des Horizontes, die Untersuchung zu führen. Man nehme irgend ein beliebiges Zeichen der Ekliptik zwischen der Mittagslinie und dem Aufgangs- oder Untergangspunkte, dies sei .

Zu der täglichen Umdrehung scheinen auch die Auf- und Untergänge der Gestirne zu gehören; nicht nur jene einfachen, über welche wir eben erst gesprochen haben, sondern auch diejenige Art, durch welche die Gestirne Morgen- und Abendsterne werden. Obgleich dies Letztere mit der jährlichen Revolution zusammenhängt: so scheint es doch am passendsten hier besprochen zu werden. Die alten Mathematiker unterscheiden wahre von scheinbaren Morgen- und Abendsternen. Bei den wahren findet der Morgen-Aufgang eines Gestirns dann statt, wenn dasselbe mit der Sonne zugleich aufgeht; der Morgen-Untergang aber dann, wenn das Gestirn bei aufgehender Sonne untergeht; und in dieser ganzen Zwischenzeit heisst es Morgen-Gestirn. Ein Abendaufgang findet aber statt, wenn das Gestirn bei untergehender Sonne aufgeht; ein Abenduntergang dagegen, wenn das Gestirn bei untergehender Sonne auch untergeht: und in dieser ganzen Zwischenzeit heisst es Abendgestirn, indem es bei Tage unsichtbar ist, und bei Nacht erscheint. Bei den scheinbaren Morgen- und Abendsternen aber findet der Morgen-Aufgang des Gestirns dann statt, wenn dasselbe mit der Morgendämmerung und vor Sonnenaufgang sich anschickt, aufzugehen und zu erscheinen beginnt; der Morgenuntergang aber dann, wenn das Gestirn bei aufgehenwollender Sonne eben unterzugehen scheint; der Abend-Aufgang dann, wenn bei der Abenddämmerung das Gestirn eben aufgeht; der Abend-Untergang aber dann, wenn das Gestirn nach Sonnenuntergang erst aufhört ferner sichtbar zu sein, und im Uebrigen von der Sonne beim Aufgehen verdeckt [89] deckt wird, bis es bei dem Morgen-Aufgange in der Reihenfolge früher erscheint. Dies verhält sich bei den Fixsternen, und auch bei den Planeten Saturn, Jupiter und Mars auf gleiche Weise. Aber Venus und Merkur gestalten ihren Auf- und Untergang anders: denn sie werden nicht, wie jene, durch die Ankunft der Sonne verdeckt, noch durch ihren Weggang aufgedeckt, sondern indem sie vorwärts schreiten, tauchen sie sich in den Glanz der Sonne und entziehen sich demselben. Jene werden beim Abend-Aufgange und beim Morgen-Untergange gar nicht unsichtbar, so dass sie mit ihrem Lichte fast die ganze Nacht hindurch leuchten. Diese aber verschwinden ohne Unterschied vom Untergange zum Aufgange, und können nicht gesehen werden. Es giebt auch noch einen andern Unterschied, dass nämlich bei jenen die wahren Morgen-Auf- und Untergänge früher eintreten, als die scheinbaren, die Abend-Auf- und Untergänge aber später, indem sie dort vor dem Aufgange der Sonne vorausgehen, hier ihrem Untergange folgen. Bei den untern Planeten aber sind die scheinbaren Morgen- und Abend-Aufgänge später als die wahren, die Untergänge dagegen früher. Die Methode aber, durch welche sie zu bestimmen sind, kann aus dem Obengesagten eingesehen werden, wo wir die schiefe Aufsteigung jedes Sterns, welcher einen bekannten Ort einnimmt, und mit welchem Grade der Ekliptik er auf- und untergeht, auseinander gesetzt haben. Wenn nun die Sonne in diesem Punkte oder in dem ihm entgegengesetzten erscheint: so hat das Gestirn einen wahren Auf- oder Untergang, Morgens oder Abends. Von diesen unterscheiden sich die scheinbaren je nach der Helligkeit und Grösse des Gestirns. Diejenigen, welche sich durch stärkeres Licht auszeichnen sind kürzere Zeit in den Sonnenstrahlen verborgen, als diejenigen, welche schwächer leuchten. Und die Grenzen des Unsichtbarseins und des Erscheinens, werden durch die unter dem Horizonte liegenden Bogen der Kreise, welche durch die Pole des Horizonts gezogen sind, zwischen dem Horizonte selbst und der Sonne bestimmt. Sie betragen für die Fixsterne erster Grösse fast 12°, für den Saturn 11°, für Jupiter 10°, für Mars 111/2°, für Venus 5°, für Merkur 10°. Im Allgemeinen aber weicht der Rest des Tageslichtes, welcher die Abend- oder Morgendämmerung ausmacht, der Nacht bei 18 Graden des schon bezeichneten Bogens; wenn die Sonne um so viele Grade unter dem Horizonte steht: so beginnen auch die kleineren Sterne sichtbar zu werden. Manche nehmen den unter dem Horizonte liegenden Parallelkreis an, und sagen, wenn die Sonne diesen berührt, es tage oder die Nacht sei beendet. Wenn wir also wissen, mit welchem Punkte der Ekliptik ein Gestirn auf- oder untergeht, und den Winkel dieses Bogens der Ekliptik mit dem Horizonte in demselben Punkte kennen, und wenn wir dann zwischen dem aufgehenden Punkte und der Sonne noch so viele Grade der Ekliptik finden, als hinreichen, um die Tiefe der Sonne unter dem Horizonte der für das gegebene Gestirn bestimmten Grenze gleich zu machen: so sagen wir, es finde sein erstes Erscheinen oder Verschwinden statt. Was wir aber über die Höhe der Sonne über dem Horizonte in den vorhergehenden Auseinandersetzungen [90] nachgewiesen haben, stimmt in Allem mit ihrem Versinken unter den Horizont überein, und unterscheidet sich nur durch die Stellung: wie denn dasjenige, was für die sichtbare Halbkugel untergeht, für die unsichtbare aufgeht. Es steht Alles in Wechselbeziehung und ist leicht einzusehen, deshalb mag das, was über den Auf- und Untergang der Gestirne, sowie über die tägliche Umdrehung des Erdballs gesagt ist, hinreichen.
Nachdem von uns die tägliche Umdrehung der Erdkugel, nebst ihren Folgen auseinandergesetzt ist: so müsste jetzt der Nachweis des jährlichen Umlaufs folgen. Wie aber einige der alten Mathematiker der Meinung gewesen sind, dass die Erscheinungen der Fixsterne, als die Grundlage der Wissenschaft, vorangehen müssen: so halten auch wir es für gut, dieser Meinung zu folgen; da wir in dem Streite der Prinzipien gegen die Hypothesen annehmen wollen, dass die Sphäre der Fixsterne überhaupt ganz unbeweglich sei, so dass die Abweichungen aller Planeten mit Recht auf dieselben bezogen werden. Niemand aber nehme daran, dass wir diese Anordnung getroffen haben, deswegen Anstoss, weil Ptolemäus in seiner „grossen Construction“ der Meinung gewesen ist, dass die Entwickelung der Fixsterne nur vorgenommen werden könne, wenn die Kenntniss der Sonnen- und Mond-Oerter vorangegangen wäre, und deshalb geglaubt hat, dass die Untersuchung über die Fixsterne bis dahin verschoben werden müsse. Wenn man dies in Bezug auf die Zahlen versteht, durch welche die scheinbare Bewegung der Sonne und des Mondes ausgedrückt wird: so mag das vielleicht richtig sein; denn auch der Geometer Menelaus hat die meisten Sterne und ihre Oerter mittelst der Mondconjunctionen in Zahlen abgeleitet. Wir werden dies aber viel besser erreichen, wenn wir aus den, mit Hülfe der Instrumente, sorgfältig geprüften Oertern der Sonne und des Mondes, irgend einen Stern bestimmen, was wir bald zeigen werden. Es dient uns auch der vergebliche Versuch derer zur Warnung, welche glaubten, dass die Grösse des Sonnenjahres einfach aus den Aequinoctien oder Solstitien, und nicht auch aus den Fixsternen abzuleiten wäre, worüber man bis auf unsere Zeiten niemals zur Uebereinstimmung gelangen konnte, so dass in keinem Capitel ein grösserer Streit bestanden hat. Dies hatte Ptolemäus im Sinne, als er das Sonnenjahr nicht ohne den Verdacht eines Irrthums, der mit der Zeit sich herausstellen könnte, zu seiner Zeit berechnet hatte, und die Nachwelt aufforderte, in dieser Angelegenheit künftig die äusserste Gewissheit zu erstreben. Es hat uns daher der Mühe werth geschienen, zu zeigen, wie mit Hülfe der Instrumente die Oerter der Sonne und des Mondes gefunden werden, um wieviel sie nämlich vom Frühlingsäquinoctium oder von [91] andern Hauptpunkten der Welt abstehen: was uns dann bei der Untersuchung der andern Gestirne von Nutzen ist, so dass wir dadurch auch die mit Glanz durchwobene Fixsternsphäre und deren Bild dem Auge darlegen. Mit welchen Instrumenten aber der Abstand der Wendekreise, die Schiefe der Ekliptik und die Neigung der Kugel oder die Höhe der Pole des Aequators gemessen werden, ist oben auseinandergesetzt. Auf dieselbe Weise können wir jede beliebige Mittagshöhe der Sonne erhalten. Diese Höhe wird uns je nach ihrem Unterschiede von der Neigung der Kugel ergeben, um wie viel die Sonne vom Aequator abweicht; und aus dieser Abweichung wird ihr, vom Aequinoctium oder Solstitium an, gerechneter Ort für den Mittag selbst erkannt. Die Sonne scheint aber in einem Zeitraume von 24 Stunden fast einen Grad zu durchlaufen, es kommen also auf den stündlichen Antheil 2½ Minuten, woraus ihr Ort für jede beliebige andere Stunde leicht berechnet werden kann.
Um nun die Oerter des Mondes und der Sterne zu beobachten, wird ein anderes Instrument construirt, welches Ptolemäus[5] Astrolabium nennt. Es werden nämlich zwei Kreise oder vierkantige Kreisringe so hergestellt, dass sie mit ihren ebenen Seiten oder Wangen die concave oder convexe Oberfläche rechtwinklig schneiden: durchweg congruent und von passlicher Grösse, damit sie nicht durch zu grosse Ausdehnung beschwerlicher zu handhaben sind, während andererseits die Grösse für eine genauere Eintheilung der Grade günstig ist. Ihre Breite und Dicke belaufe sich aber wenigstens auf den dreissigsten Theil des Durchmessers. Sie werden alsdann rechtwinklig gegeneinander zusammengefügt und verbunden, so dass sie mit ihren convexen und concaven Seiten an einander passen, als ob sie der Rundung einer Kugel angehörten. Von diesen nehme nun der eine die Stelle der Ekliptik, der andere die Stelle desjenigen Kreises ein, welcher durch die Pole des Aequators und der Ekliptik geht. Der die Ekliptik vorstellende Kreis ist an den Seiten in gleiche Theile, gewöhnlich 360, zu theilen, welche wieder Unterabtheilungen erhalten, so weit es das Instrument zulässt. Auf dem andern Kreise werden von der Ekliptik aus Quadranten abgemessen, und dort die Pole der Ekliptik bezeichnet; von diesen nimmt man, nach Maassgabe der Schiefe der Ekliptik, Abstände und bezeichnet hier die Pole des Aequators. Nachdem dies so eingerichtet ist, werden zwei andere Kreise durch die Pole der construirten Ekliptik gelegt, um welche Pole der eine ausserhalb, der andere innerhalb sich bewegen soll. Ihre Dicken zwischen den beiden ebenen Flächen sind gleich, die Breiten der Wangen aber sind ähnlich denen jener Kreise; und sie sind so gepasst, dass die concave Oberfläche des grösseren, die convexe; und die convexe Oberfläche des kleineren die concave Oberfläche der Ekliptik überall berührt; so jedoch, dass ihre Bewegung nicht gehindert wird, sondern dass die Ekliptik mit ihrem Meridiane, und jene gegenseitig aneinander vorübergehen können. Diese Kreise durchbohrt man mit Sorgfalt diametral, sowie auch jene Pole der Ekliptik, und fügt ihnen Axen ein, durch welche sie verbunden und geleitet werden. [92] Der innere Kreis ist ebenfalls in 360 gleiche Theile getheilt, so dass in den einzelnen Quadranten an den Polen 90 steht. In seiner Rundung ist überdem ein anderer, also ein fünfter, in derselben Ebene drehbarer Kreis anzubringen, an dessen Wangen ein paar Platten, in diametraler Richtung, mit Oeffnungen oder Stiften befestigt sind, an denen das Licht des Sternes, wie bei Dioptern, einfallen und durchgehen kann. Im Durchmesser des Kreises sind noch auf beiden Seiten Marken angefügt, als Indexe der Zahlen des umschliessenden Kreises um die Breiten auf demselben abzulesen. Endlich ist noch ein sechster Kreis erforderlich, welcher das ganze Astrolabium umfasst, in den Punkten der Pole des Aequators an Stiften hält, auf einer Säule ruht, und durch diese gegen die Ebene des Horizonts senkrecht eingestellt und befestigt ist. Nachdem auch die Pole, der Neigung der Kugel gemäss, eingestellt sind, stehe der Meridiankreis in der natürlichen Lage des Meridians, und wanke durchaus nicht aus derselben. Wenn wir, nach dieser Einrichtung des Instruments, den Ort irgend eines Sternes aufnehmen wollen: so stellen wir gegen Abend, oder wenn die Sonne eben untergehen will, und zu einer Zeit, wo wir auch den Mond in Sicht haben, den äussern Kreis auf den Grad der Ekliptik, in welchem wir nach dem Früheren die Sonne wissen, und wenden die Kreistheile nach der Sonne selbst, bis jeder von beiden, nämlich die Ekliptik und der äussere durch ihre Pole gehende Kreis sich gleichmässig beschatten; dann wenden wir den inneren Kreis nach dem Monde, und nachdem wir das Auge in seine Ebene gebracht haben, wo wir den Mond gleichsam durch die Ebene geschnitten sehen: notiren wir den Ort in der Ekliptik des Instruments; dies wird die Länge des Ortes des Mondes sein. Ohne diesen gäbe es nämlich keinen Weg für die Feststellung der Sternörter, da derselbe allein unter Allen zugleich dem Tage und der Nacht angehört. Darauf, wenn die Nacht hereinbricht, und der Stern, dessen Ort wir suchen, schon gesehen werden kann, richten wir den äussern Kreis nach dem Monde, wodurch wir die Stellung des Astrolabiums ebenso auf den Mond einstellen, wie wir es auf die Sonne gethan hatten. Dann wenden wir ebenso den inneren Kreis nach dem Sterne, bis er an der Ebene des Kreises zu hangen scheint, und durch die Diopter, welche sich auf dem eingeschlossenen Kreise befinden, gesehen wird. Auf diese Weise erhalten wir die Länge und Breite des Sternes. Während dies gethan wird, sieht man nach, welcher Grad der Ekliptik culminirt, und daraus ergiebt sich mit Gewissheit die Zeit, zu welcher die Beobachtung gemacht ist. So findet z. B. Ptolemäus[6], — welcher im zweiten Jahre des Kaisers Antoninus Pins, am neunten Tage des Pharmuthi, des achten Monats der Aegypter, in Alexandrien, beim Untergange der Sonne, den Ort desjenigen Sternes beobachten wollte, welcher, an der Brust des Löwen, Basiliskus oder Regulus genannt wird, — an dem auf die eben untergehende Sonne eingestellten Astrolabium, — nachdem fünf Nachtgleichen-Stunden seit Mittag verflossen waren, und während die Sonne in 31/24 Grad der Fische stand, — durch den eingestellten innern Kreis, dass der Mond von [93] der Sonne um 921/8 Grade abstand; wonach damals der Ort des Mondes in 51/6 Grad der Zwillinge erschien. Nach einer halben Stunde, wodurch die sechste Stunde nach Mittag voll wurde, und als der Stern bereits sichtbar zu werden begonnen hatte, und als der 4te Grad der Zwillinge culminirte: richtete er den äusseren Kreis des Instruments auf den eben erhaltenen Ort des Mondes, und erhielt, durch das Verschieben des inneren Kreises, den Abstand des Sternes von dem Monde, in der Reihenfolge der Zeichen, zu 571/10 Grad. Weil also der Mond von der untergehenden Sonne, wie bemerkt, um 921/8 Grad abstand, welcher Winkel den Mond auf 51/6 Grad der Zwillinge bestimmte, — während einer halben Stunde aber, der Mond um 1/4 Grad sich fortbewegt hat, da die stündliche Grösse der Mondsbewegung ungefähr 1/2 Grad beträgt. — aber wegen des damaligen Abnehmens des Mondes das halbstündige Fortrücken desselben etwas, ungefähr 1/12, kleiner als 1/4 sein musste, weshalb der Mond in 51/3 Grad der Zwillinge stand, — (wenn wir erst die Mondsveränderungen abgehandelt haben werden, so wird sich ergeben, dass die Differenz nicht so gross gewesen ist, so dass es klar werden wird, der gesehene Ort des Mondes habe um mehr, als 1/3, und kaum weniger, als um 2/5 die 5 Grade der Zwillinge überschritten), — und wenn hiezu 571/10 Grade addirt werden: — so ergiebt sich der Ort des Sternes in 21/2 Grad des Löwen, also von der Sonnenwende fast um 321/2 Grade abstehend, bei einer nördlichen Breite von 1/6 Grad. Hier war der Ort des Basiliskus, aus welchem auch die Stellungen der anderen Fixsterne sich ergaben. Diese Beobachtung des Ptolemäus ist angestellt nach den Römern im Jahre Christi 139 den 24 Februar, im ersten Jahre der 229sten Olympiade. So ermittelte jener hervorragendste Mathematiker, welchen Ort zu jener Zeit jeder Stern in Bezug auf das Frühlingsäquinoctium einnahm und gab die Helligkeit der Himmelskörper an, wodurch er unserm Studium bedeutende Dienste leistete, und uns in der schweren Arbeit so unterstützte, dass wir, die wir der Meinung sind, die Sternörter seien nicht auf die Aequinoctien, welche sich mit der Zeit ändern, sondern vielmehr die Aequinoctien auf die Sphäre der Fixsterne zu beziehen, die Bestimmung der Sterne leicht auf irgend einen andern unveränderlichen Anfangspunkt beziehen können, nämlich auf den Widder, als das erste Zeichen, und zwar auf dessen ersten Stern, welcher im Kopfe desselben steht. Dabei wurde angenommen, dass diejenigen, welche gleichsam angeheftet und unter sich zusammenhängend an ihren für immer eingenommenen Stellen leuchten, immer ein und dasselbe unwandelbare Ansehen behalten. Sie sind aber durch die bewunderungswürdige Mühe und Sorgfalt der Alten in 48 Bilder eingetheilt, mit Ausnahme derjenigen, welche ein Kreis, der die für das vierte, ungefähr durch Rhodos gehende, Klima stets unsichtbaren Sterne abtrennt. Diese Sterne blieben ebenso formlos, wie sie unbekannt waren. Nach des jüngeren Theon’s Meinung sind in der Aratischen Beschreibung die Sterne aus keiner anderen Ursache in Sternenbilder geordnet, als um ihre so grosse Menge einzutheilen, und sie nach altem Brauche mit gewissen Benennungen einzeln [94] zu bezeichnen; wie es feststeht, dass schon bei Hiob[7] einige benannt waren, und wir auch bei Hesiod und Homer[8] die Namen der Plejaden, Hyaden, des Arcturus und Orion lesen. Bei ihrer Bezeichnung nach der Länge bedienen wir uns also nicht der Eintheilung in zwölf Theile, welche von den Aequinoctien und den Sonnenwenden beginnen, sondern der einfachen und gewohnten Zahlen der Grade; im Uebrigen folgen wir dem Ptolemäus, mit Ausnahme weniger, von denen wir erkannt haben, dass sie entweder verfälscht sind, oder sich sonst anders verhalten. In wie fern aber ihr Abstand von jenen Hauptpunkten zugänglich ist, wollen wir im folgenden Buche lehren.[9]
Anmerkungen [des Übersetzers]
- ↑ [14] 55) Almagest I. 14.
- ↑ [14] 56) Almagest I. 11.
- ↑ [14] 57) In der Säcular-Ausgabe findet sich diese Angabe im Manuscripte so: 23° 52′ 20″; dies würde aber mit der Schlussbemerkung dieses Capitels im Widerspruche stehen, nach welcher die Schiefe der Ekliptik niemals grösser, als 23° 52′ gewesen sein soll.
- ↑ [14] 58) Die hier angeführten Namen und Bezeichnungen sind, mit Ausnahme von Byzanz, dieselben, welche in der von Schreckenfuchs in Basel 1551 besorgten lateinischen Ausgabe des Almagest pag. 154 sich finden. Danach haben die von den Alten unterschiedenen sieben Climate folgende Begrenzungen:
Nr. Bezeichnung. Nördliche Breite Dauer des längsten Tages Grad Min. Stunde Min. 1 Meroë 16 27 13 0 2 Syëne 23 50 13 30 3 Unter-Aegypten 30 22 14 0 4 Rhodus 36 0 14 30 5 Hellespont 40 56 15 0 6 Mittlerer Pontus 45 0 15 30 7 Mündung des Borysthenes (Dnjepr) 48 32 16 0 - ↑ [14] 59) Almagest V. 1.
- ↑ [14] 60) Diese Beobachtung findet sich: Almagest VII. 2. Die Reduction des ägyptischen Datum’s derselben lässt sich leicht folgendermassen ausführen. Das erste ägyptische Regierungsjahr des Augustus beginnt am 31sten August, oder am 1sten Thoth, also am 243sten Tage des 4684sten Jahres der julianischen Periode, 12 Uhr Mittags nach Alexandriner Zeit, vergl. Jdeler, Handbuch, I. 157. — Seit Anfang der julianischen Periode bis auf Augustus waren also verstrichen: 4683a 242d 12h julianisch. Das Intervall zwischen Augustus und Aelius Antoninus, welcher Letztere mit Antoninus Pius des Textes identisch ist, beträgt 166 ägyptische Jahre. Die in Rede stehende Beobachtung hat am 9ten Pharmuthi, also am 219ten Tage des zweiten Jahres des Antoninus Pius, also 167a 218d ägyptisch, oder
167a 176d 6h julianisch nach Augustus stattgefunden, addirt man also hierzu jene 4683 242 12, so erhält man 4851a 53d 18h, nach dem Anfange der julianischen Periode. Der Anfang der christlichen Zeitrechnung liegt aber 4713a später, als der Anfang der julianischen Periode, vergl. Jdeler, Handbuch, I. 77, folglich fand die Beobachtung statt 138a 53d 18h nach Christus, d. h. 6h Abends am 24sten Februar 139 nach Christus, wie auch Copernicus im Texte angiebt. Der Wettlaufssieg des Coröbus zu Olympia, mit welchem die alle vier Jahre, ungefähr am ersten Juli regelmässig wiederkehrende Feier der olympischen Spiele, und also auch die Zeitrechnung der Griechen nach Olympiaden beginnt, — fand statt am ersten Juli des Jahres 776 vor Christus, — Jdeler, Handbuch, I. 375, — oder im 3938ten Jahre der julianischen Periode, — a. a. O. I. 77. — Zieht man diese Zeit von der Zeit der Beobachtung ab, also
[15] 228 Olympiaden 1a 237d 18h. Weil aber die Beobachtung in die erste Hälfte des betreffenden Jahres fällt, so muss der Rest bei der Division mit vier um eins vermindert werden, alsovon 4851a 53d 18h 3937 181 so erhält man 913a 237d 18h, und diese Anzahl der Jahre mit vier dividirt, giebt erhält man
228 Olympiaden 0a 237d 18h d. h. im ersten Jahre der 229sten Olympiade, was mit Copernicus’ Angabe im Texte wiederum übereinstimmt.
Copernicus kannte die hier angewandte julianische Periode nicht, weil dieselbe erst vierzig Jahre nach seinem Tode von Joseph Scaliger in seinem Werke „de emendatione temporum Paris 1583“, durch Multiplication der drei cyklischen Zahlen 28, 19 und 15 gebildet wurde. Hiernach nehmen, mit dem Anfange dieser Periode, Sonnen-, Mond- und Judictionscirkel zugleich ihren Anfang, und beginnt diese Periode nach je 7980 julianischen Jahren von Neuem. Innerhalb einer solchen Periode wird also jedes Jahr durch seine eigenthümlichen cyklischen Zahlen characterisirt. Nun war für das erste Jahr der christlichen Zeitrechnung der Sonnencirkel 10, die güldene Zahl 2 und die Zinszahl 4, woraus sich ergiebt, dass das 4714te Jahr der julianischen Periode das erste Jahr nach Christus ist. Vergl. Jdeler, Handbuch, II. 587. –
- ↑ [15] 61) Hiob. Cp. 9. V. 9. „Er machet den Wagen am Himmel, und Orion, und die Glucke, und die Sterne gegen Mittag.“
- ↑ [15] 62) Bei Homer findet sich, Ilias XVIII, 486,
„Πληϊάδας ϑ᾽ Ὑάδας τε, τό τε σϑένος Ὠρίωνος“. welcher Vers auch bei Hesiod, ἔργα καὶ ἡμέραι 615, wörtlich übereinstimmend vorkommt. Ferner gehört hierher: Homer, Odyssee V
- 271. – – „οὐδέ οἱ ὕπνος ἐπὶ βλεφάροισιν ἔπιπτεν
- 272. Πληϊάδας τ᾽ ἐσορῶντι ϰαὶ ὀψὲ δύοντα Βοώτην
- 273. Ἄρκτον ϑ᾽, ἣν ϰαὶ ἄμαξαν ἐπίκλησιν καλέουσιν,
- 274. ἥτ᾽ αὐτοῦ στρέφεται καί τ᾽ Ὠρίωνα δοκεύει.“
Der Vers 273 findet sich auch, Ilias XVIII 487, wörtlich wieder, und doch erwähnt Copernicus im Texte weder Arktos noch den Wagen, ἄμαξα, bei dieser Gelegenheit.
Hesiodus a. a. O. 560 & 610 nennt den Arctur, versteht aber darunter wahrscheinlich das ganze Gestirn des Bootes. Die Pleiaden nennt er. 383 u. 615, auch Ἀτλαγενεῖς.
Orion wird ausser an den angeführten Stellen noch erwähnt von Hesiodus 598 u. 619, von Homer, Ilias XXII. 29.
- ↑ [15] 63) Der Schluss dieses Capitels ist nach dem Wortlaute der Nürnberger Ausgabe wiedergegeben, obgleich aus der Thorner Säcular-Ausgabe hervorgeht, dass derselbe in der Original-Handschrift etwas davon abweicht. Namentlich ist in Letzterer die Berufung auf Hiob ausgestrichen, und an deren Stelle diejenige auf Hesiod und Homer gesetzt. Sollte Copernicus sich deswegen zu dieser Abänderung veranlasst gefühlt haben, weil es ihm bereits zweifelhaft erschien, ob Hiob eine historische Person sei, und ob deshalb das Buch Hiob ein so hohes Alter besitze, dass es zum Beweise des „alten Brauches“ einiger Sternnamen angeführt werden könne?
| ← Erstes Buch | Nach oben | Zweites Buch Teil B → |
| Fertig! Dieser Text wurde zweimal anhand der Quelle Korrektur gelesen. Die Schreibweise folgt dem Originaltext. |





















































































































